اعتبار سنجی متقابل (Cross Validation) – به زبان ساده

اغلب در مدل‌سازی، بخصوص در مبحث «آموزش ماشین» (Machine Learning)، احتیاج به برآورد پارامترهای مدل داریم. در صورتی که تعداد پارامترها زیاد باشد، پیچیدگی مدل زیاد شده و ممکن است محاسبات به سادگی قابل انجام نباشند. اعتبارسنجی متقابل یکی از راه‌هایی است که می‌توان تعداد پارامترها (متغیرهای) مدل را بصورت بهینه تعیین کرد.

برای مثال می‌دانیم که در «رگرسیون خطی» (Linear Regression) بر اساس یک نمونه تصادفی دو یا چند بعدی از متغیر پاسخ و متغیرهای مستقل، هدف برآورد پارامترهای مدل است. این کار با استفاده از کمینه سازی تابع مربعات خطا صورت می‌گیرد. بنابراین مشخص است که برآورد پارامترهای مدل به شکلی صورت گرفته که برای مشاهدات ثبت شده، میانگین مربعات خطا حداقل ممکن خواهد بود.

با افزایش پارامترهای مدل (افزایش متغیرها مستقل)، کارایی مدل افزایش خواهد یافت، زیرا میانگین مربعات برای نمونه جمع‌آوری شده به هر حال با افزایش متغیرها کاهش خواهد یافت. بنابراین مناسب‌ترین مدل برای نمونه با حداکثر تعداد پارامتر بدست آمده است. برآورد پارامترهای حاصل از این نمونه را به اصطلاح «برآوردهای درون-نمونه‌ای» (In-sample Estimation) می‌نامند.

ولی اگر این مدل، برای نمونه دیگری از همان جامعه به کار رود، شاید مناسب محسوب نشود. به نظر می‌رسد افزایش متغیرها، ممکن است به کارایی مدل آسیب برساند. چنین مشکلی را با نام «بیش‌برازش» (Overfitting) می‌شناسیم. راه حل برای چنین مسئله‌ای می‌تواند استفاده از «اعتبارسنجی متقابل» یا «اعتبارسنجی متقاطع» (Cross Validation) باشد که هدف در آن تعیین تعداد متغیرها (پارامترهای) مناسب مدل است. گاهی به این روش، «برآورد گردشی» (Rotation Estimation) یا «آزمایش خارج از نمونه» (Out-of-sample testing) نیز می‌گویند.

در چنین حالتی، به پارامترهایی که توسط اعتبارسنجی متقابل برآورد می‌شوند، «برآوردهای بیرون-نمونه‌ای» (Out-of-sample Estimation) می‌گویند.

برای آشنایی بیشتر با مفهوم بیش‌برازش بهتر است مطلب بیش برازش (Overfitting)، کم برازش (Underfitting) و برازش مناسب --- مفهوم و شناسایی را قبلا مطالعه کرده باشید. از آنجایی که در این نوشتار به مباحث مرتبط با رگرسیون اشاره می‌کنیم، مطالعه رگرسیون خطی --- مفهوم و محاسبات به زبان ساده خالی از لطف نیست.

اعتبارسنجی متقابل

برای سنجش کارایی یک مدل، معمولا دو روش به کار گرفته می‌شود: ۱- ارزیابی براساس فرضیاتی که باید مدل در آن‌ها صدق کند. ۲- ارزیابی براساس کارایی مدل در پیش‌بینی مقدارهای جدید (مشاهده نشده).

برای بررسی و ارزیابی مدل براساس رویه شماره ۱، تکیه بر داده‌هایی است که مشاهده شده‌ و در ساختن مدل به کار رفته‌اند. برای مثال در رگرسیون خطی، فرض بر این است که باقی‌مانده‌های مدل رگرسیونی باید تصادفی و با واریانس ثابت باشند. همچنین توزیع آن‌ها نیز باید نرمال باشد. بررسی صحت این فرضیات می‌تواند به عنوان معیاری برای سنجش اعتبار مدل محسوب شود. همانطور که می‌دانید، پارامترهای مدل رگرسیونی با کمینه سازی مربعات خطا حاصل می‌شود. بنابراین انتظار داریم که مدل ساخته شده نسبت به هر مدل دیگری مجموع کمترین مجموع مربعات خطا را نیز داشته باشد.

مشخص است که بررسی موارد بالا براساس داده‌هایی که مدل براساس آن ساخته شده است،‌ میسر است ولی نمی‌توان کارایی مدل را برای داده‌های جدیدی که هنگام مدل‌سازی مشاهده نشده‌اند، سنجید.

اما در اعتبارسنجی متقابل، تکیه بر داده‌هایی است که مشاهده شده‌اند ولی در هنگام ساختن مدل به کار گرفته نمی‌شوند. این داده‌ها به منظور بررسی و سنجش کارایی مدل برای پیش‌بینی داده‌‌های جدید به کار می‌روند.

به این ترتیب برای اندازه‌گیری کارایی مدل و بهینه بودن آن متوسل به برآورد خطای مدل براساس داده‌هایی می‌شویم که برای اعتبارسنجی متقابل کنار گذاشته شده‌اند. برآورد این خطا را معمولا «خطای خارج از نمونه» (Out-of-sample error) می‌نامند. در این نوشتار، به بررسی اعتبارسنجی متقابل به عنوان ابزاری برای اندازه‌گیری این خطا، پرداخته و شیوه‌های مختلف پیاده‌سازی آن را بررسی می‌کنیم.

در تصویر زیر، نمودار مربوط به روند تغییرات خطای مدل براساس داده‌های آموزشی و داده‌های آزمایشی براساس پیچیدگی مدل (تعداد پارامترها) ترسیم شده است. خطوط کم‌رنگ آبی و قرمز، خطای مدل برای داده‌های آموزشی و آزمایشی را برحسب تعداد پارامترها نشان می‌دهند. همچنین خط آبی پررنگ، میانگین خطای مدل برای داده‌های آموزشی و خط قرمز پررنگ نیز میانگین خطای مدل برای داده‌های آزمایشی است.

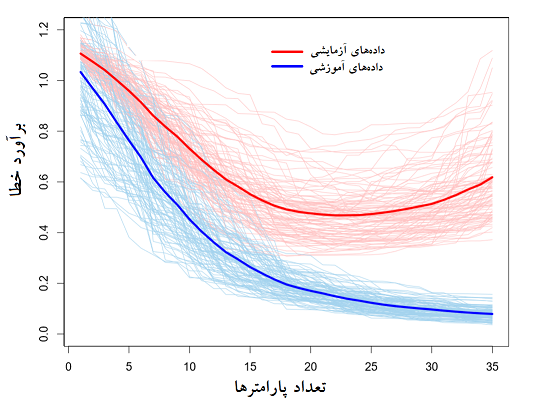
با توجه به این نمودار مشخص است که با افزایش تعداد پارامترهای مدل، میزان خطای مدل براساس داده‌های آموزشی کاهش یافته است. ولی برآورد خطای مدل براساس داده‌های آزمایشی ابتدا نزولی بوده و در زمانی که تعداد پارامترهای مدل (پیچیدگی مدل) از میزانی بیشتر شده (مثلا ۲۰ پارامتر) افزایشی شده است. این اثر دقیقا همان مشکل «بیش‌برازش» است که به کمک اعتبارسنجی متقابل سعی در رفع آن می‌کنیم.

تنظیم پارامترها به کمک اعتبارسنجی متقابل

فرض کنید مشاهداتی از جامعه به صورت یک نمونه تصادفی در دسترس است که قرار است از آن‌ها در مدل‌سازی استفاده شود. هدف در اعتبارسنجی متقابل، دستیابی به مدلی است که تعداد پارامترهای آن بهینه باشد. یعنی پیدا کردن مدلی است که دچار بیش‌برازش نباشد. برای برای دستیابی به این هدف در «آموزش ماشین» (Machine Learning) معمولا داده‌ها را به دو قسمت تفکیک می‌کنند.

• قسمت داده‌های آموزشی (Training set): از این بخش از داده‌ها به منظور ایجاد مدل و برآورد پارامترهای آن استفاده می‌شود.
• قسمت داده‌های آزمایشی (Test set): این قسمت از داده‌ها برای بررسی کارایی مدل استفاده می‌شود. اهمیت این بخش از داده‌ها در این نکته است که این مشاهدات شامل مقدارهای متغیرهای مستقل (xها) و پاسخی (y) هستند که در مدل به کار نرفته ولی امکان مقایسه مقدار پبش‌بینی شده ($$\widehat{y}$$) را با مقدار واقعی به ما می‌دهند. البته توجه داریم که این داده‌ها مدل را تحت تاثیر قرار نداده‌اند، پس در تعیین پارامترهای مدل نقشی نداشته و فقط برای ارزیابی مدل به کار می‌روند.

با توجه به تفکیکی که برای این دو گروه داده در نظر گرفته شد، مدل‌سازی فقط براساس بخش داده‌های آموزشی خواهد بود. ولی در روش اعتبارسنجی متقابل که از این به بعد آن را به اختصار «CV» می‌نامیم، طی یک فرآیند تکرار شونده، قسمت داده‌های آموزشی (Training set) که به منظور مدل‌سازی به کار می رود، خود به دو بخش تفکیک می‌شود. در هر بار تکرار فرآیند CV، بخشی از داده‌ها برای آموزش و بخشی دیگر برای آزمایش مدل به کار می‌رود. به این ترتیب این فرآیند یک روش باز‌نمونه‌گیری به منظور برآورد خطای مدل محسوب می‌شود.

نسبت این قسمت‌ها نیز البته جای بحث دارد که در این نوشتار به آن نمی‌پردازیم ولی معمولا ۵۰ درصد کل داده‌ها به منظور آموزش، ۲۵ درصد نیز برای اعتبارسنجی متقابل و مابقی داده‌ها برای آزمایش مدل در نظر گرفته می‌شود.

نکته: باید توجه داشت که داده‌های آزمایشی در فرایند CV ممکن است در تکرار بعدی به عنوان داده‌های آموزشی به کار روند، در نتیجه ماهیت آن‌ها با داده‌هایی که در قسمت قبل به عنوان داده‌های آزمایشی (Test set) معرفی شد، متفاوت است.

شاید تصویر زیر به درک ماهیت داده‌های تست در فرآیند CV کمک کند. مشخص است که داده‌های اعتبارسنجی بخشی از داده‌های آموزشی هستند و داده‌های آزمایشی نیز به عنوان بخشی مجزا از داده‌هایی آموزشی فرض شده‌اند. مراحل تکرار فرآیند CV نیز در تصویر به خوبی دیده می‌شود. نکته دیگری که در تصویر مشخص است، مکمل بودن مجموعه داده‌های آموزشی و اعتبارسنجی است. با انتخاب بخشی از داده‌ها برای انجام فرایند CV، بقیه داده‌ها برای آموزش به کار گرفته می‌شوند.

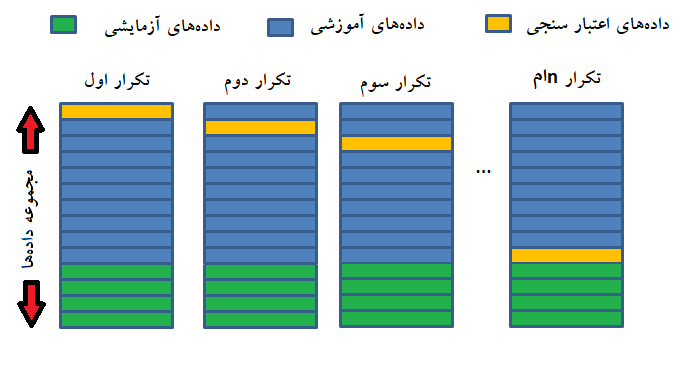
در هر مرحله از فرایند CV، مدل بدست آمده توسط داده‌های آزمایشی برای پیش‌بینی داده‌های CV به کار گرفته و «خطا» (Error) یا «دقت» (Accuracy) حاصل از برازش مدل روی داده‌های CV محاسبه می‌شود. معمولا میانگین این خطاها (دقت‌ها) به عنوان خطای (دقت) کلی مدل در نظر گرفته می‌شود. البته بهتر است انحراف معیار خطاها (دقت‌ها) نیز گزارش شود. به این ترتیب با توجه به تعداد پارامترهای مختلف (پیچیدگی مدل)، می‌توان مدل‌های متفاوتی تولید و خطای برآورد آن‌ها را به کمک روش CV‌ اندازه‌گیری کرد. در انتها مدلی را به عنوان مدل مناسب انتخاب خواهیم کرد که دارای کمترین برآورد خطا باشد.

روش‌های مختلف اعتبارسنجی متقابل

براساس شیوه و روش انتخاب مجموعه داده‌های اعتبارسنجی، گونه‌های مختلفی از روش‌های CV معرفی شده‌اند. در ادامه به معرفی بعضی از این گونه‌ها می‌پردازیم.

فیلم آموزش معرفی برخی از ابزارهای داده کاوی (رایگان) در فرادرس

کلیک کنید

روش Holdout

در این روش به طور تصادفی، داده‌ها به دو بخش آموزشی و اعتبارسنجی تقسیم می‌شود. پارامترهای مدل توسط داده‌های آموزشی برآورد شده و برآورد خطای مدل نیز براساس داده‌‌های اعتبارسنجی محاسبه می‌شود.

سادگی محاسبات و عدم تکرار فرآیند CV در این روش از مزیت‌های آن محسوب می‌شود. اگر داده‌های مربوط به بخش آموزش و اعتبارسنجی همگن باشند، این روش مناسب به نظر می‌رسد. ولی از آنجایی که محاسبات خطای مدل براساس فقط یک مجموعه داده، بدست آمده ممکن است برآورد مناسبی برای خطای مدل ارائه نشود.

روش Leave-One-Out

در اینجا به مانند روش باز‌نمونه‌گیری جک نایف، از مجموعه داده‌های آموزشی یکی مشاهده خارج شده و براساس بقیه مشاهدات،‌ پارامترها برآورد می‌شود. سپس میزان خطای مدل برای مشاهده خارج شده، محاسبه می‌شود. از آنجایی در این روش در هر مرحله از فرآیند CV فقط یکی از مشاهدات خارج می‌شود، تعداد مراحل تکرار فرآیند CV با تعداد داده‌های آموزشی برابر است. در نتیجه زمان محاسبه خطای مدل کوتاه بوده و به راحتی نیز قابل پیاده‌سازی است. گاهی به اختصار این روش را LOO می‌نامند.

شبه کد زیر می‌تواند مراحل اجرای این روش CV را بهتر نشان دهد.

همانطور که در کد بالا دیده می‌شود، در مرحله iام، مشاهده iام از مجموعه داده‌های آموزشی خارج شده و مدل توسط تابع Interpolate برآورد شده و مقدار تخمینی برای متغیر پاسخ در مشاهده iام توسط مدل بدست می‌آید. مربع فاصله مقدار واقعی متغیر پاسخ ([y[i) از مقدار برآورد شده (y_out)، نیز به عنوان برآورد خطای مدل در نظر گرفته شده و در انتها، میانگین خطای همه مدل‌ها به عنوان برآورد خطای کلی محاسبه شده است.

روش Leave-P-Out

اگر در روش LOO، تعداد مشاهداتی که از مجموعه داده‌های آموزشی خارج می‌شوند برابر با p‌ باشد، آن را روش (Leave-p-Out) یا به اختصار LPO می‌نامند. در نتیجه اگر n تعداد مشاهدات در مجموعه داده‌های آموزشی باشد، تعداد مراحل اجرای فرآیند CV برابر با $${n \choose p}$$ خواهد بود.

به این ترتیب در هر مرحله از فرآیند، p‌ مشاهده از داده‌های آموزشی، خارج شده و براساس بقیه پارامترها، مدل برآورد می‌شود. سپس خطای مدل برای p مشاهده خارج شده محاسبه می‌شود. در انتها نیز با محاسبه میانگین خطاهای بدست آمده، برآورد خطای مدل حاصل خواهد شد.

برای مثال اگر تعداد مشاهدات برابر با n=100 و p=30 باشد، تعداد مراحل فرآیند CV برابر است با:

$${100 \choose 30}=3 \times 10^{25}$$

که شاید عملا مقایسه این تعداد مدل میسر نباشد.

روش k-Fold

اگر مجموعه داده‌های آموزشی را به طور تصادفی به k زیرنمونه یا «لایه» (Fold) با حجم یکسان تفکیک کنیم، می‌توان در هر مرحله از فرایند CV، تعداد k-1 از این لایه‌ها را به عنوان مجموعه داده آموزشی و یکی را به عنوان مجموعه داده اعتبارسنجی در نظر گرفت. تصویر زیر، مراحل روش k-Fold را به خوبی نشان می‌دهد. مشخص است که با انتخاب k=10، تعداد تکرارهای فرآیند CV برابر با ۱۰ خواهد بود و دستیابی به مدل مناسب به سرعت امکان‌پذیر می‌شود.

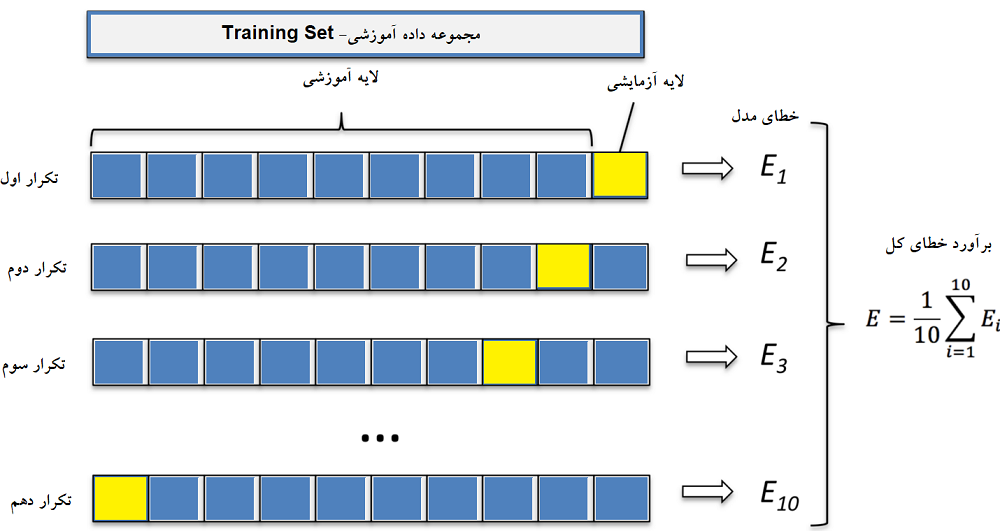
اعتبارسنجی براساس تکرار تصادفی باز‌نمونه‌گیری

در این روش که گاهی به «اعتبارسنجی مونت کارلو» (Monte Calro Cross Validation) معروف است، مجموعه داده به طور تصادفی به دو بخش آموزش و اعتبارسنجی تفکیک می‌شود. سپس پارامترهای مدل براساس داده‌های آموزش برآورد شده و خطا یا دقت مدل نیز به کمک داده‌های اعتبارسنجی محاسبه می‌شود. با تکرار تفکیک تصادفی داده‌ها، میانگین خطا یا دقت مدل‌ها، به عنوان معیار انتخاب مدل مناسب در نظر گرفته می‌شود (کمترین خطا یا بیشترین دقت).

فیلم آموزش مبانی انتخاب ویژگی Feature Selection در داده کاوی در فرادرس

کلیک کنید

با توجه به انتخاب تصادفی داده‌ها، نسبت حجم داده‌های آموزشی و اعتبارسنجی به تعداد تکرار‌ها وابسته نخواهد بود و برخلاف روش k-Fold می‌توان با هر تعداد،‌ فرآیند CV را انجام داد. ولی در عوض به دلیل انتخاب تصادفی زیرنمونه‌ها، ممکن است بعضی از مشاهدات هرگز در بخش اعتبارسنجی به کار گرفته نشده و بعضی دیگر بیش از یکبار در محاسبات برآورد خطای مدل به کار روند.

اگر تعداد تفکیک‌های تصادفی در این روش به سمت بی‌نهایت میل کند، نتایج حاصل از اعتبارسنجی به سمت نتایج حاصل از روش Leave-P-Out میل می‌کند. همچنین در حالت «طبقه‌ای روش مونت کارلو» (Stratified Monte Carlo Validation)، نمونه‌های تصادفی به شکلی انتخاب می‌شوند که میانگین متغیر پاسخ (مثلا متغیر وابسته در بحث رگرسیون) برای هر زیرنمونه‌ها یکسان باشد. این کار زمانی که متغیر پاسخ به صورت باینری باشد، می‌تواند باعث متعادل شدن نمونه‌ها شود.

برای مثال فرض کنید، تعداد صفرها به طور مشخصی از تعداد ۱‌ها بیشتر یا کمتر باشد. این حالت زمانی اتفاق می‌افتد که طبقه‌ها از لحاظ تعداد مشاهدات یکسان یا متعادل نباشند. به این ترتیب روش CV طبقه‌ای مونت کارلو، باعث می‌شود که نسبت مشاهدات با مقدار ۰ و ۱ برای متغیر پاسخ، در بین مجموعه داده‌های آموزش و اعتبارسنجی حفظ شود.

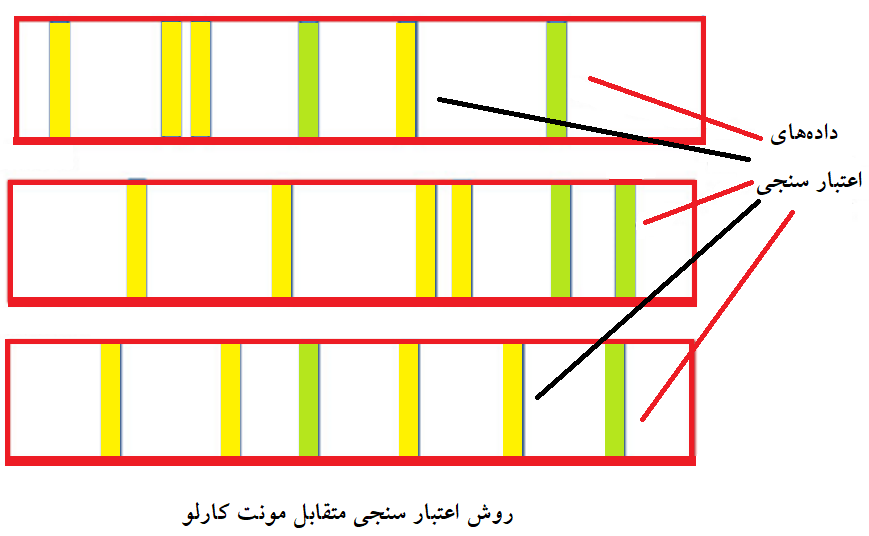
در تصویر بالا شیوه انتخاب در روش CV مونت کارلو دیده می‌شود. همانطور که دیده می‌شود ممکن است در مراحل انتخاب زیرنمونه‌های تصادفی، گاهی بعضی از مشاهدات انتخاب نشده و گاهی نیز تعداد انتخاب بعضی مشاهدات بیش از یکبار باشد. هر کادر قرمز رنگ نشان دهنده یکبار فرآیند CV است که در آن چندین مشاهده به عنوان زیرنمونه اعتبارسنجی متقابل در نظر گرفته شده است.

مستطیل‌های زرد رنگ مشاهداتی هستند که فقط یکبار در زیرنمونه‌ها دیده شده‌اند و مستطیل‌های سبز رنگ نیز مشاهداتی هستند که دوبار در زیرنمونه‌ها به کار رفته‌اند. مشاهداتی که در قسمت سفید رنگ هستند، داده‌های آموزشی محسوب شده‌اند که ممکن است هرگز در فرآیند CV قرار نگرفته و در برآورد خطای کل نقشی نداشته باشند.

معایب روش اعتبارسنجی متقابل

هرچند این روش، براساس داده‌ها، قادر به برآورد خطای کلی مدل است، ولی بسیار به آن‌ها بخصوص تعداد داده‌ها وابسته است. بنابراین اگر تعداد نمونه یا مشاهدات کاهش یابد، دقت برآورد و یا حتی امکان استفاده از این روش مشکل آفرین خواهد بود. در نتیجه وجود حجم نمونه مناسب و هم‌توزیع بودن داده‌ها در میان مجموعه داده‌های آموزشی، آزمایشی و اعتبارسنجی از اهمیت زیادی در صحت نتایج حاصل از فرآیند CV برخوردار است.

اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش های داده کاوی یا Data Mining در متلب
• آموزش تخمین خطای طبقه بندی یا Classifier Error Estimation
• آموزش داده کاوی در RapidMiner
• آموزش یادگیری ماشین
• مجموعه آموزش‌های نرم‌افزارهای آماری
• بیش برازش (Overfitting)، کم برازش (Underfitting) و برازش مناسب --- مفهوم و شناسایی
• نمونه‌گیری و بازنمونه‌گیری آماری (Sampling and Resampling) — به زبان
• روش‌های بازنمونه‌گیری جک نایف و بوت استرپ (Jackknife and Bootstrap) — به زبان ساده
  
• ماشین بردار پشتیبان — به همراه کدنویسی پایتون و R

^^