دترمینان یک ماتریس و محاسبه آن — به زبان ساده (+ فیلم آموزش رایگان)
دترمینان (Determinant) ماتریس، عدد مخصوصی است که برای ماتریسهای مربع محاسبه می شود. ماتریس، آرایش منظمی از اعداد است که در سطرها و ستونهای معینی ترتیب یافتهاند. برای مثال در تصویر زیر یک ماتریس با دو سطر و دو ستون مشاهده میکنید:
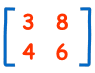
دترمینان این ماتریس برابر است با (روش محاسبه بعدا توضیح داده می شود):
(3 × 6) - (8 × 4) = 18 - 32 = -14
در این مطلب از مجله فرادرس با تعریف دیترمینان ماتریس و چگونگی محاسبه آن آشنا میشویم.
کاربرد این عدد چیست؟
دترمینان اطلاعاتی در مورد ماتریس در اختیارمان می گذارد که در سیستم های معادلات خطی به درد می خورد. این عدد برای یافتن معکوس ماتریس و همچنین در معادلات دیفرانسیل و انتگرال و در شرایط بسیار دیگری به درد می خورد. اگر دترمینان ماتریسی مخالف صفر باشد، آنگاه در مییابیم که آن ماتریس معکوسپذیر است. از این رو از طریق دترمینان میتوان مقادیر ویژه یک ماتریس یا به عبارت بهتر یک نگاشت خطی از آن تعیین کرد. با استفاده از دترمینان میتوان معکوس ماتریسهای ۳×۳ و مراتب بالاتر را محاسبه کرد. حتی میتوان جهت حل معادله درجه ۳ از آنالیز ماتریسی و مفهوم دترمینان استفاده کرد.
نماد
نماد دترمینان، دو خط عمودی در طرفین حرف انگلیسی ماتریس مورد نظر است. برای مثال | A | به معنی دترمینان ماتریس A است. در واقع این نماد دقیقاً هم شکل نماد «قدر مطلق» است.
محاسبه دترمینان
اولین شرط برای محاسبه دترمینان این است که ماتریس باید مربع باشد، یعنی تعداد سطرها و ستونهای آن با هم برابر باشند. در صورتی که این شرط برقرار باشد با چند رابطه ساده حسابی میتوان دترمینان ماتریس را محاسبه کرد. روش محاسبه دترمینان برای ماتریسهای با اندازه مختلف در ادامه توضیح داده شده است. البته در مواردی که با ماتریسهای با مرتبه بالاتر روبرو هستیم، بایستی از مفاهیمی همچون ماتریس کهاد یا ترانهاده ماتریس نیز بهره برد.
برای یک ماتریس 2×2
برای یک ماتریس 2×2 یعنی ماتریسی که دارای 2 سطر و 2 ستون است:
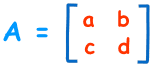
دترمینان برابر است با:
| A | = ad-bc
یعنی دترمینان ماتریس A برابر است با a ضرب در d منهای b ضرب در c. اگر یک علامت ضربدر روی ماتریس تصور کنید، به خاطر سپردن رابطه فوف آسان تر خواهد بود:
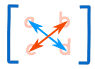
- آبی قسمت مثبت محاسبه دترمینان است (ad+)
- قرمز قسمت منفی محاسبه دترمینان است (bc-)
مثال:
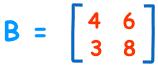
| B | = 4 × 8-6 × 3
= 32-18
= 14
محاسبه دترمینان ماتریس 3x3
برای یک ماتریس 3×3 یعنی ماتریسی که دارای 3 سطر و 3 ستون است:
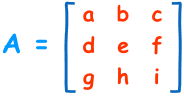
دترمینان برابر است با:
| A | = a (ei - fh) - b (di - fg) + c (dh - eg)
به نظر پیچیده می آید، اما الگوی کار به شکل زیر است:
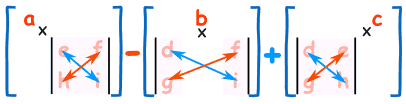
برای یافتن دترمیان یک ماتریس 3x3 مراحل زیر را اجرا میکنیم:
- ابتدا دترمینان ماتریس 2x2 که هیچ درایه آن در سطر و ستون a قرار ندارد را محاسبه میکنیم و سپس a را در این مقدار ضرب می کنیم.
- در مورد b و در مورد c نیز همین عمل را تکرار می کنیم.
- مقادیر بدست آمده را باهم جمع می کنیم، اما به یاد داشته باشید که از مقدار منفی عدد b در جمع استفاده میکنیم.
موارد فوق را در به صورت تصویر زیر فرمول بندی کردهایم. توجه داشته باشید که علامت | | به معنی «دترمینان»است:
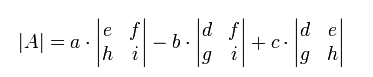
مثال:
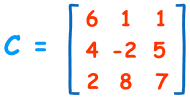
| C |= 6 × ( -2 × 7-5 × 8 )-1 × ( 4 × 7-5 × 2 ) + 1 × ( 4 × 8-(-2) × 2 )
= 6 × ( -54 )-1 × ( 18 ) + 1 × ( 36 )
=-306
محاسبه دترمینان ماتریس های 4x4 و بالاتر
این الگو برای ماتریس های 4x4 نیز صدق می کند. در مطالب قبلی مجله فرادرس در مورد روش محاسبه ماتریسهای 3 در 3 صحبت کردیم. در مورد ماتریسهای 4 در 4 روش عمل به صورت زیر خواهد بود:
- مثبت a ضرب در دترمینان ماتریسی که در سطر و ستون a نیست.
- منفی b ضرب در دترمینان ماتریسی که در سطر و ستون b نیست.
- مثبت c ضرب در دترمینان ماتریسی که در سطر و ستون c نیست.
- منفی d ضرب در دترمینان ماتریسی که در سطر و ستون d نیست.

فرمول آن را به صورت تصویر زیر میتوان نمایش داد:
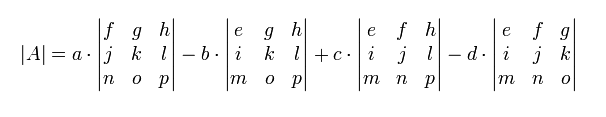
به الگوی -+-+ دقت کنید (... a … -b … + c … -d+). این الگو را باید به خاطر بسپارید.
این الگو برای ماتریس های 5x5 و بالاتر نیز صدق می کند. اما برای این محاسبه دترمینان این نوع ماتریس ها بهتر است از نرمافزار هایی که به این منظور طراحی شدهاند، استفاده کنیم.
روشهای دیگری نیز برای محاسبه دترمینان وجود دارند
این روش محاسبه ای که در بخش فوق اشاره کردیم به نام روش «بسط لاپلاس» نامیده می شود. این روش میان دانش آموزان رایج است چرا که حفظ کردن آن آسان است. اما باید بدانید که روش های دیگری نیز برای محاسبه دترمینان یک ماتریس وجود دارند.
آزمون دترمینان یک ماتریس
در این بخش به منظور درک بهتر چگونگی محاسبه ماتریسهای متفاوت، چند پرسش چهار گزینهای مطرح شده است.
دترمینان ماتریس زیر برابر است با:
۲۲
۲۴
۲-
۲
دترمینان ماتریسی ۲ در ۲ به صورت زیر محاسبه میشود:
در نتیجه، دترمینان ماتریس برابر است با:
معکوس ماتریس برابر است با:
معکوس ماتریس ۲ در ۲ به صورت زیر بهدست میآید:
اگر دترمینان ماتریس A برابر صفر باشد، این ماتریس معکوس نخواهد داشت. برای بهدست آوردن معکوس ماتریس ابتدا دترمینام آن را بهدست میآوریم:
از آنجا که دترمینان این ماتریس، مخالف صفر است، کعکوس آن را میتوانیم بهدست آوریم:
معکوس ماتریس برابر است با:
معکوس این ماتریس وجود ندارد.
معکوس ماتریس ۲ در ۲ به صورت زیر بهدست میآید:
اگر دترمینان ماتریس A برابر صفر باشد، این ماتریس معکوس نخواهد داشت. برای بهدست آوردن معکوس ماتریس ابتدا دترمینان آن را بهدست میآوریم:
این ماتریس، معکوس ندارد، زیرا دترمینان آن برابر صفر است.
به ازای چه مقدار از ، ماتریس B معکوس ماتریس A است؟
این مسئله را میتوانیم با دو روش حل کنیم.
روش اول
ابتدا معکوس ماتریس A را بهدست میآوریم، سپس آن را برابر ماتریس B قرار میدهیم. معکوس ماتریس A به صورت زیر محاسبه میشود:
در ادامه، ماتریس B را برابر ماتریس قرار میدهیم و مقدار را بهدست میآوریم:
با برابر قرار دادن تکتک مولفهها، مقدار برابر بهدست میآید.
روش دوم
اگر باشد، داریم:
در رابطه فوق، I ماتریس واحد است. برای بهدست آوردن مقدار دو ماتریس A و B را در یکدیگر ضری میکنیم و حاصل را برابر ماتریس واحد قرار میدهیم:
به ازای چه مقدار از ماتریس A معکوس ندارد؟
ماتریس هنگامی معکوس دارد که دترمینان آن مخالف صفر باشد. بنابراین، اگر دترمینان ماتریسی برابر صفر شود، آن ماتریس، معکوس نخواهد داشت. در صورت مسئله، ماترس A داده شده است. مقدار را باید به گونهای بهدست آوریم که این ماتریس، معکوس نداشته باشد. برای انجام این کار دترمینان ماتریس را محاسبه و برابر صفر قرار میدهیم:
دترمینان ماتریس زیر کدام است؟
۲۳
۲۳-
۲۱
۲۰
برای ماتریس 3×3 یعنی ماتریسی که دارای 3 سطر و 3 ستون است:
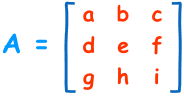
دترمینان با استفاده از رابطه زیر بهدست میآید:
محاسبه دترمینا ماتریس ۳ در ۳ به صورت تصویری در عکس زیر نشان داده شده است:

برای یافتن دترمیان ماتریس مراحل زیر را طی میکنیم:
- ابتدا دترمینان ماتریس 2x2 که هیچ درایه آن در سطر و ستون a قرار ندارد را محاسبه میکنیم و سپس a را در این مقدار ضرب می کنیم.
- در مورد b و در مورد c نیز همین عمل را تکرار می کنیم.
- مقادیر بدست آمده را باهم جمع می کنیم، اما به یاد داشته باشید که از مقدار منفی عدد b در جمع استفاده میکنیم.
با توجه به توضیحات فوق دترمینان ماتریس به صورت زیر محاسبه میشود:
$$\begin{bmatrix} 7 & -4 & 2 \\ 3 & 1 & -5\\ 2 & 2 & -5 \end{bmatrix}= 7 \times det(\begin{bmatrix}1 & -5 \\ 2 & -5 \end{bmatrix}) - (-4)\times det (\begin{bmatrix} 3 & -5 \\2 & -5 \end{bmatrix}) + 2 \times det(\begin{bmatrix} 3 & 1 \\ 2 & 2\end{bmatrix}) \\ = 7 ( 5 ) + 4 ( -5) + 2 ( 4) = 23
دترمینان ماتریس واحد ۳ در ۳ برابر است با:
۱
۱-
صفر
هیچکدام
ماتریس واحد به صورت زیر نوشته میشود:
دترمینان این ماتریس ۳ در ۳ به صورت زیر محاسبه میشود:
به ازای چه مقدار از ماتریس معکوس ندارد؟
۳ و ۴
۳- و ۴
۳- و ۴-
هیچکدام
ماتریس در صورتی معکوس ندارد که دترمینان آن برابر صفر باشد. از اینرو، برای بهدست آوردن باید دترمینان ماتریس را بهدست آوریم. در حالت کلی، دترمینان ماتریس 3×3 به صورت زیر محاسبه میشود:
برای یافتن دترمیان ماتریس مراحل زیر را طی میکنیم:
- ابتدا دترمینان ماتریس 2x2 که هیچ درایه آن در سطر و ستون a قرار ندارد را محاسبه میکنیم و سپس a را در این مقدار ضرب می کنیم.
- در مورد b و در مورد c نیز همین عمل را تکرار می کنیم.
- مقادیر بدست آمده را باهم جمع می کنیم، اما به یاد داشته باشید که از مقدار منفی عدد b در جمع استفاده میکنیم.
دترمینان ماتریس f برابر است با:
det(\begin{bmatrix} 2 & 0 & 10 \\ 0 & 7+x & -3\\ 0 & 4 & x \end{bmatrix}) = 0\\= 2 \times det(\begin{bmatrix}7+x & -3 \\ 4 &x \end{bmatrix}) - (0)\times det (\begin{bmatrix} 0 & -3 \\0 & x \end{bmatrix}) + (10) \times det(\begin{bmatrix} 0 & 7+x \\ 0 & 4\end{bmatrix}) = 0 \\ = 2 ((7+x) (x) -(-3) (4))= 2 (7x + x ^ 2 +12) = 0 \\ x ^ 2 + 7x + 12 = 0 \\ (x + 3 ) (x + 4) = 0 \\x = -3 ,x = -4 $$
دترمینان ماتریس ۴ در ۴ زیر کدام است؟
۶۰۰
۷۰۰
۸۰۰
هیچکدام
برای محاسبه دترمینان ماتریسهای ۴ در ۴ به صورت زیر عمل میکنیم:
- مثبت a ضرب در دترمینان ماتریسی که در سطر و ستون a نیست.
- منفی b ضرب در دترمینان ماتریسی که در سطر و ستون b نیست.
- مثبت c ضرب در دترمینان ماتریسی که در سطر و ستون c نیست.
- منفی d ضرب در دترمینان ماتریسی که در سطر و ستون d نیست.
فرمول آن را به صورت زیر نوشت:
به الگوی -+-+ دقت کنید (... a … -b … + c … -d+). این الگو را باید به خاطر بسپارید. مقدار دترمینان ماتریس داده شده پس از انجام محاسبات برابر ۹۰۰ بهدست میآید.
جمعبندی
- برای ماتریس 2x2 دترمینان برابر است با ad-bc
- برای ماتریس 3x3 مقدار a را در دترمینان ماتریس 2x2 که در سطر و یا ستون a نیست، ضرب میکنیم. سپس b و c را نیز به همین ترتیب ادامه می دهیم. اما به یاد داشته باشید که b می بایست منفی شود.
- این الگو برای ماتریس های بزرگتر نیز صدق می کند: a را در ماتریسی که در سطر و ستون a نیست ضرب کنید. سپس برای b این کار را انجام دهید و به همین ترتیب ادامه می دهید، اما الگوی -+-+ را همواره به یاد داشته باشید و مقادیر به دست آمده را یکی در میان منفی کنید.












عالی
فقط 3 در 3 بود که پس بالاترش کو؟!
بسیار عالی
ساده و قابل درک بود
عالی
مفید بود👌
سلام
فقط خواستم به نوبه خودم بی نهایت سپاس گذاری کنم
شما کمک بسیار بزرگی در زمینه آموزش بودید
خدا قوت
سلام
به روش ساروس دترمینان ماتریس 4*4 یا بالاتر هم می شه محاسبه کرد ؟
بسیار عالی
سلام، ممنون ، عالی. خدا خیرتون بده
مرسی خیلی عالی بود
فهمیدم🌸🌱
بسیار زیبا و مرحله به مرحله و قشنگ توضیح دادند.
با سلام
سپاس بابت مطالب خوب و آموزنده
خدا قوت
عالی بود . عالییییییییی
بسیار زیبا و ساده و خوب توضیح داده شد. من از ماتریس هیچ چیز نمیدونستم. الان مسلط شدم.
یاشا
دمتون گرم
مرسی از آموزش هایی که میزارید.وتقعا ممنون
با سلام بسیار عالی و کاربردی
سایتتون فوق العاده است.مخصوصا فیلمای کمک اموزشی
ممنون ازسایت خوبتون.خیلی عالی بود
سلام عالی بود فقط تنها چیزی که من نفهمیدم در بخش تابع نمایی وln هاست که مربوط به بخش دیگری است وخواستم اگر میشه یکذره در اون قسمت ها روان تر اموزش دهید ولی کلا به جز اون دو تا همه اموزش های سایتتون عالیه خدا قوت به همگی
خیلیم خوب
وری گود
واقعا عالی بود چندین مطلب از سایت شما خوندم و نظرم در مورد ریاضی کاملا تغییر کرد سالها این مطالب را میخواندم ولی ترکی از انها نداشتم تو امتحان هم با تقلب نمره میگرفتم ولی اینبار با فهم کامل میرم سر جلسه امتحان
بسیار عالی
سلام، درود بر شما و سپاسگزارم
سلام، عالی بود سپاسگزارم
تشکرمیکنم
خیلی کمک کننده بود ممنون از سایت خوبتون !
بسیار شیوا و روان توضیح داده شده بود. ممنون از فرادرس عزیز که همیشه بهترینه. تیمتان همواره برقرار?
عالی ممنون
خیلی خوب بود یه چیز ساده میخواستم که هم سریع یاد بگیرم هم بتونم به حافظه بسپارم
خدا خیرتون بده
واقعا مطالب این پست بدردم خورد
مرسی از نویسنده ی پست
عالییییی!!!
ممنون .. ساده و گویا
مرسی خیلی خوب بود
واقعا ممنننننننننننننوووووووون
قطعا کسی که فن بیان خوبی داره در همه امور موفقه و قطعا شما جزوموفق ترین افراد هستید ممنونم ازتون
دنبال یه مطلبی بودم که سریع دترمینان رو برام یاداوری کنه و این سایت این کارو بخوبی کرد ممنونم
عالی بود
مفید بود ممنون
خوب بود ولی یکم ناقص هست.چندتا بند اضافه در مورد خاصیت های دترمینان ضرر نداره.ممنون
Ok
بسيار عالي بود
بسيار عالي بود
افتضاح بود..
نه اتفاقا خیلی خوب بود
چرا؟خوب بود که
ساده، زیبا و جذاب. هنر یعنی این.
ساده و آسان و قابل فهم بود.
خیلی ماهید .اینقد گلید شمااااااااااااااا مرررررررررسی اساتید خوب
خیلی ممنون عالی بود