فرمول های فیزیک دهم در یک نگاه

فیزیک دهم یا فیزیک یک در سال اول متوسطه یا مقطع دهم برای رشتههای ریاضیفیزیک و علومتجربی تدریس میشود. چهار فصل از فیزیک دهم شامل مبحثهای اندازهگیری، ویژگیهای فیزیکی مواد، کار، انرژی و توان و دما و گرما در دو رشته ریاضی و فیزیک مشترک هستند. علاوه بر چهار فصل نامبرده، مبحث ترمودینامیک در فصل پنجم از فیزیک دهم به دانشآموزان رشته ریاضیفیزیک تدریس میشود. حل مسئله و درک فرمول های فیزیک دهم برای موفقیت در آزمون نهایی فیزیک، بسیار مهم و ضروری است.
در این مطلب از مجله فرادرس، فرمول های فیزیک دهم را به صورت خلاصه همراه با حل مثال توضیح میدهیم. برای هر فصل، ابتدا فرمولها به صورت خلاصه در جدول نوشته شدهاند، سپس توضیح کوتاهی همراه با حل چند مثال برای هر فرمول آورده شده است.
فرمول های فیزیک دهم فصل اول
فرمولهای فصل اول فیزیک دهم در جدول زیر به صورت خلاصه نوشته شدهاند.
| مبحث موردنظر | فرمول های فیزیک دهم فصل اول |
| تبدیل یکاها (مثال تبدیل گرم به کیلوگرم) | |
| چگالی |
در فصل اول از فیزیک دهم، در مورد اندازهگیری صحبت میشود. در این فصل ابتدا با کمیتهای اصلی و فرعی آشنا میشویم. هفت کمیت اصلی در فیزیک وجود دارند که نام آنها، یکای اندازهگیری و نمادِ یکا در جدول زیر نوشته شدهاند.
| کمیت | نام یکا | نماد یکا |
| طول | متر | m |
| جرم | کیلوگرم | kg |
| زمان | ثانیه | s |
| دما | کلوین | K |
| مقدار ماده | مول | mol |
| جریان الکتریکی | آمپر | A |
| شدت روشنایی | کندلا (شمع) | cd |
کمیتهای فرعی در فیزیک از کمیتهای اصلی و با توجه به فرمول فیزیکی مورداستفاده ساخته میشوند. در بیشتر مواقع و به هنگام حل مسائل فیزیک لازم است یکای کمیتی را تغییر دهیم. به عنوان مثال، اگر در مسئلهای در فیزیک، جرم جسم بسیار کوچکی برحسب گرم بیان شده باشد، شاید لازم باشد آن را به کیلوگرم تبدیل کنیم. بنابراین، آشنایی با چگونگی تبدیل یکاها به یکدیگر بسیار ضروری است. برای انجام این کار از روش تبدیل زنجیرهای استفاده میکنیم. به عنوان مثال، چون یک کیلوگرم برابر ۱۰۰۰ گرم است، داریم:
هر دو کسر بالا برابر یک هستند، بنابراین میتوان هر یک از آنها را به عنوان ضریب تبدیل به کار برد. فرض کنید جرم جسمی برابر ۴۵ گرم است. برای تبدیل آن به کیلوگرم به صورت زیر عمل میکنیم:
سازگاری یکاها
هر کمیت فیزیکی با نماد مشخصی نشان داده میشود. به عنوان مثال، اندازه نیرو را با F و جرم را با m نشان میدهیم. کمیتهای فیزیکی را میتوان به کمک رابطهها و معادلههای حاکم، به یکدیگر مربوط ساخت. به هنگام استفاده از روابط و معادلات فیزیکی، باید به این نکته توجه داشته باشیم که یکاها در دو طرف رابطه با یکدیگر سازگار باشند.
نمادگذاری علمی
به هنگام مطالعه اتمها یا کیهان به ترتیب با مقدارهای بسیار کوچم و بزرگ سروکار داریم. برای سهولت در نوشتن و خواندk این اعداد بسیار بزرگ یا بسیار کوچک از روشی به نام نمادگذاری علمی استفاده میکنیم. نمادگذاری علمی از سه بخش تشکیل شده است:
- عددی بین یک تا ده
- توان صحیحی از ۱۰
- یکای کمیت
چگالی
اگر جرم ماه همگنی برابر m و حجم آن برابر باشد، چگالی آن، ، به صورت زیر نوشته میشود:
یکای اندازهگیری چگالی در سیستم SI برابر کیلوگرم بر مترمکعب () است. چگالی برحسب گرم بر سانتیمتر مکعب نیز بیان میشود.
مثال اول تبدیل واحد
۵۰ میکرومتر چند نانومتر است؟
برای تبدیل میکرومتر به نانومتر، ابتدا عدد داده شده برحسب میکرومتر را به متر، سپس آن را به نانومتر تبدیل میکنیم. هر میکرومتر برابر متر است.
برابر است. عدد بهدست آمده برحسب متر را به نانومتر تبدیل میکنیم.
مثال دوم تبدیل واحد
جسمی با سرعت ۱۰۸ میکرومتر بر ساعت () حرکت میکند. این سرعت برحسب متر بر ثانیه چه مقدار است؟
جسمی با سرعت ۱۰۸ میکرومتر بر ثانیه حرکت میکند. برای تبدیل سرعت جسم به کیلومتر بر ساعت، ابتدا آن را به متر بر ثانیه و سپس به کیلومتر بر ساعت تبدیل میکنیو.
تبدیل سرعت از به
یک میکرومتر برابر متر است.
تبدیل سرعت از به
مثال چگالی
چگالی آب برابر ۱۰۰۰ کیلوگرم بر مترمکعب و چگالی بنزین برابر ۶۸۰ کیلوگرم بر مترمکعب است. چرا آب مایع مناسبی برای خاموش کردن بنزین شعلهور نیست؟
آب مایع مناسبی برای خاموش کردن بنزین شعلهور نیست، زیرا چگالی بنزین از آب کمتر است و روی آن شناور خواهد ماند. این بدان معنا است که با ریختن آب روی بنزین شعلهور، آب منجر به پخش شدن بنزین و شدیدتر شدن آتش میشود.
فرمول های فیزیک دهم فصل دوم
در فصل دوم از فیزیک دهم ابتدا با حالتهای مختلف ماده، سپس با تعریف نیروهای بینمولکولی و اثرات آن آشنا میشویم. فرمولهای فصل دوم فیزیک دهم در جدول زیر به صورت خلاصه نوشته شدهاند.
| مبحث موردنظر | فرمول های فیزیک دهم فصل دوم |
| فشار وارد شده به سطح | |
| فشار در عمق مشخصی از شاره | |
| فشار پیمانهای و فشار مطلق | |
| بالابر هیدرولیک | |
| معادله پیوستگی |
در ادامه، فرمولهای نوشته شده در جدول فوق را با حل مثال به صورت خلاصه توضیح میدهیم.
فشار چیست؟
رابطه فشار یکی از مهمترین فرمول های فیزیک دهم است. فشار برابر نسبتِ نیروی عمودی وارد شده بر سطح جسم بر مساحت سطح موردنظر است. تعریف فشار بسیار ساده به نظر میرسد، نیروی وارد شده بر واحد سطح. واحد نیرو در SI برابر نیوتن (N) و واحد سطح برابر مترمربع () است. بنابراین، واحد فشار در SI برابر یا نیوتن بر متر مربع است. به واحد فشار، پاسکال (Pa) نیز گفته میشود.
قبل از حل مسائل مربوط به فشار، توجه به این نکته مهم است که در رابطه داده شده برای فشار، سه نوع مسئله ممکن است مطرح شود:
- مساحت و نیرو داده شدهاند. در این صورت فشار وارد شده را از تقسیم نیرو بر مساحت بهدست میآوریم.
- مساحت و فشار داده شدهاند. در این صورت نیروی وارد شده را از حاصلضرب فشار در مساحت بهدست میآوریم.
- فشار و نیرو داده شدهاند. در این صورت مساحت سطح را از تقسیم نیرو بر فشار بهدست میآوریم.

مثال محاسبه فشار
جعبهای به جرم دو کیلوگرم و طول ۳۰ سانتیمتر، عرض ۱۵ سانتیمتر و ارتفاع ۱۰ سانتیمتر روی زمین قرار دارد. نسبت بزرگترین فشار به کمترین فشار وارد شده از طرف آجر بر زمین کدام یک از گزینههای زیر است؟ (شتاب جاذبه زمین برابر ۱۰ متر بر مجذور ثانیه است)
۳
۴
یک
۲
فشار با استفاده از رابطه زیر بهدست میآید:
نیرو در این مثال، وزن آجر و برابر است با:
همانطور که در رابطه فشار دیده میشود، هرچه مساحت سطح تماس بیشتر باشد، فشار کمتر و هرچه این مساحت، کمتر باشد، فشار وارد شده بر سطح بیشتر خواهد بود. برای بهدست آوردن بیشترین فشارِ وارد شده از سمت جعبه بر زمین، باید آن را به گونهای روی زمین قرار دهیم که کمترین سطح تماس را داشته باشد. همچنین، برای بهدست آوردن کمترین فشارِ وارد شده از سمت جعبه بر زمین، باید آن را به گونهای روی زمین قرار دهیم که بیشترین سطح تماس با زمین بهدست بیاید.
برای انجام این کار و دانستن آنکه کدام وجه جعبه بیشترین مساحت و کدام یک، کمترین مساحت را دارد، مساحت هر وجه را جداگانه محاسبه میکنیم. توجه به این نکته مهم است که مساحت باید برحسب مترمربع بهدست بیاید.
بیشترین مساحت برابر ۰/۰۴۵ مترمربع و کمترین مساحت برابر ۰/۰۱۵ متر مربع است. بنابراین، بیشترین فشار وارد شده از سمت آجر بر زمین برابر است با:
به طور مشابه، کمترین فشار وارد شده از سمت آجر بر زمین برابر است با:
در نتیجه نسبت بیشترین فشار به کمترین فشار برابر است با:
فشار در شاره ها
هر فشاری به سیستم از سمت محیط اطراف وارد شود، به طور مساوی و یکنواخت در سراسر آن توزیع خواهد شد. این تعریف به عنوان اصل پاسکال شناخته میشود. اصل پاسکال، تنها برای فشار خارج از مایع به کار برده میشود. سوالی که ممکن است مطرح شود آن است که فشار داخل مایع چگونه تغییر میکند.
با در نظر گرفتن هوای بالای مایع، فشار کل یا فشار مطلق در ارتفاع h از سطح آن برابر است با:
به فشار کل (شامل فشار جو)، فشار مطلق گفته میشود. به بیان دیگر، فشار مطلق، فشار را نسبت به خلأ مطلق اندازه میگیرد. بنابراین، مقدار آن برای تمام فشارهای بالاتر از خلأ مطلق، مثبت و برای خلأ مطلق، برابر صفر است. مقدار فشار مطلق هرگز نمیتواند منفی باشد. فشار مطلق برابر حاصل جمع فشار پیمانهای و فشار اتمسفر است:

برای بهدست آوردن فشار در عمق h برای مایعی ساکن و در تماس با هوا در نزدیکی سطح زمین، فشار پیمانهای و فشار مطلق به صورت زیر نوشته میشوند:
مثال اول محاسبه فشار در لوله U شکل
لوله U شکلی را به صورت نشان داده شده در تصویر زیر در نظر بگیرید. لوله از دو طرف با هوا در تماس است. سمت راست لوله را با آب و سمت چپ آن را با روغنی سبک با چگالی ۷۹۰ کیلوگرم بر مترمکعب پر میکنیم. ارتفاع آب در سمت چپِلوله برابر ۷۰ سانتیمتر و نسبت ارتفاع روغن به آب در لوله سمت راست برابر ۶ است. ارتفاع روغن در لوله سمت راست چه مقدار است؟
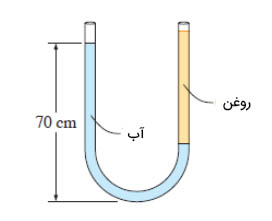
۶۴/۴ سانتیمتر
۷۳/۲ سانتیمتر
۸۵/۳ سانتیمتر
۹۶/۱ سانتیمتر
ارتفاع آب در سمت چپ لوله برابر ۷۰ سانتیمتر یا ۰/۷۰ متر است. ارتفاع آب و روغن در سمت راست لوله را به ترتیب با و نشان میدهیم. بر طبق صورت سوال، ارتفاع روغن در سمت راست لوله ۶ برابر ارتفاع آب است، بنابراین:
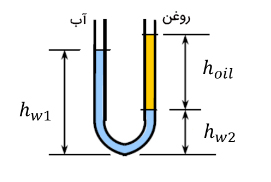
سطح آب و روغن با هوا در تماس هستند. اگر فشار کفِ لوله برابر و فشار اتمسفر برابر باشند، برای نیمه چپ لوله را میتوانیم به صورت زیر بنویسیم:
همچنین، برای نیمه راستِ لوله داریم:
دو معادله بالا با یکدیگر برابر هستند:
را از دو طرف رابطه فوق حذف میکنیم:
است، بنابراین:
با حذف g از طرفین رابطه فوق، داریم:
با قرار دادن چگالی آب، روغن و ارتفاع آب در لوله سمت چپ و ارتفاع روغن در لوله سمت راست را بهدست میآوریم:
با توجه به آنکه است، ارتفاع روغن در سمتِ راست لوله برابر است با؛
مثال فشارسنج
فشارسنجی متشکل از دو مایع را در نظر بگیرید که به صورت نشان داده شده در تصویر زیر به مخزنی حاوی هوا وصل شده است. اگر «چگالی نسبی» (Specific Gravity | SG) یکی از مایع بنفشرنگ برابر ۱۳/۵۵ باشد. چگالی نسبی مایع دیگر چه مقدار است؟ (چگالی هوا را برابر ۱۰۰ کیلوپاسکال در نظر بگیرید)
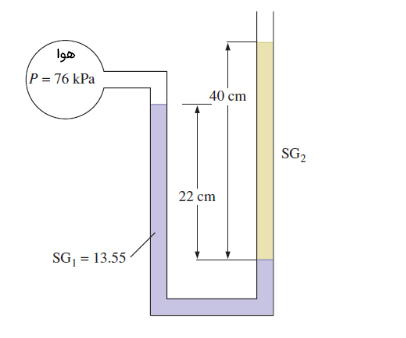
۰/۹۱
۱/۳۴
۱/۷۵
۲/۰۸
نقطه شروع را مخزن هوا در نظر میگیریم و در امتداد لوله به سمت راست حرکت میکنیم. به این نکته توجه داشته باشید که با حرکت به سمت پایین، جمع و با حرکت به سمت بالای لوله، کم میکنیم:
برای نوشتن رابطه فوق، از فشار اتمسفر شروع میکنیم و به سمت پایین لوله حرکت میکنیم. بنابراین فشار اتمسفر باید با فشار مایع شماره یک یا مایع بنفشرنگ، جمع شود. سپس، با رسیدن به کف لوله باید به سمت بالا حرکت کنیم. از اینرو، فشار مایع دوم باید از مجموع فشار هوا و فشار ناشی از مایع اول کم شود. به نسبت چگالی ماده به چگالی آب، چگالی نسبی گفته میشود. بنابراین، و را میتوانیم به صورت زیر بنویسیم:
با قرار دادن دو رابطه فوق در رابطه ، میتوانیم آن را به صورت زیر بنویسیم:
به صورت زیر بهدست میآید:
در پایان، مقدارهای داده شده را در رابطه بهدست آمه برای قرار میدهیم و مقدار آن را بهدست میآوریم:
بالابر هیدرولیک چیست؟
در بالابرهای هیدرولیک از سیستم استوانهای هیدرولیک برای بالا بردن، حرکت و جابجایی اجسام سنگین استفاده میشود. هیدرولیک بالابر سادهای در تصویر زیر نشان داده شده است.
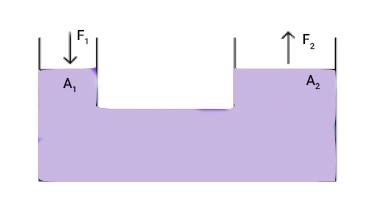
اگر نیرویی به بزرگی بر پیستون سمت چپ به مساحت وارد شود، نیرویی برابر بر پیستون سمت راست به مساحت وارد میشود به گونهای که:
مثال بالابر هیدرولیک
اتومبیلی به جرم ۱۵۰۰ کیلوگرم روی پیستون بزرگتر بالابر هیدرولیکی به شعاع ۴ متر قرار گرفته است. کمینه نیروی لازم برای بالا بردن اتومبیل چه مقدار است؟

۱۴۷۰۰۰ نیوتن
۱۵۷۰۰۰ نیوتن
۱۴۷۰۰ نیوتن
۱۶۷۰۰۰ نیوتن
نیروی جاذبه زمین، نیرویی به سمت پایین و برابر mg بر ماشین وارد میکند. در مقابل، پیستون نیز نیرویی برابر به سمت بالا بر ماشین وارد میکند. بنابراین، مقدار کمینه نیروی وارد شده از طرق پیستون برای بالا بردن ماشین با سرعت ثابت، برابر mg است. اگر مقدار از mg بیشتر شود، ماشین با شتاب شروع به حرکت به سمت بالا خواهد کرد. برای آنکه ماشین را با سرعت ثابت به سمت بالا حرکت دهیم، نیروی باید برابر mg باشد.
شاره در حرکت و اصل برنولی
بر طبق اصل برنولی، شاره در حال حرکت با سرعت بیشتر، فشار کمتری نسبت به شاره در حال حرکت با سرعت کمتر دارد. در نتیجه، در لوله آب افقی با قطر متغیر، ناحیهای که در آن، آب با سرعت بیشتری حرکت میکند دارای فشار کمتری خواهد بود.
معادله پیوستگی
معادله پیوستگی یکی از فرمولهای شارهای با جریان لایهای را در نظر بگیرید که در لولهای با دو سطح مقطع متفاوت در حال حرکت است. در حالت ایستا و در مدت زمان مشابه، جرم شاره عبوری از هر سطح مقطعِ داخل لوله، یکسان است. بنابراین، معادله پیوستگی برای شاره تراکمناپذیر به صورت زیر نوشته میشود:
مثال معادله پیوستگی
آشپزی به منظور کسب اطمینان از داشتن شیر برای پخت شیرینی، لولهای استوانهای را از انبار به آشپزخانه نصب کرده است. سر لوله با شعاع ۶ سانتیمتر در انبار قرار دارد و شیر نارگیل با سرعت ۰/۵۰ متر بر ثانیه وارد آن میشود. اگر شیر با سرعت ۲ متر بر ثانیه از انتهای لوله (انتهای لوله در آشپزخانه قرار دارد) خارج شود، شعاع انتهای لوله چه مقدار است؟
یک سانتیمتر
۲ سانتیمتر
۴ سانتیمتر
۳ سانتیمتر
معادله پیوستگی به صورت زیر نوشته میشود:
از آنجایی که سطح مقطع استوانه به صورت محاسبه میشود، بنابراین با قرار دادن آن در رابطه بالا داریم:
با حذف از دو طرف رابطه بالا داریم:
با قرار دادن دادههای پرسش در رابطه بالا خواهیم داشت:
فرمول های فیزیک دهم فصل سوم
فرمول های فیزیک دهم در فصل سوم رابطه های فیزیکی بین کار، انرژی و توان را بیان میکنند. ابتدا فرمولهای این فصل را به صورت خلاصه بیان، سپس چند مسئله را در این رابطه با یکدیگر حل میکنیم. فرمولهای فصل سوم فیزیک دهم در جدول زیر به صورت خلاصه نوشته شدهاند.
| مبحث موردنظر | فرمول های فیزیک دهم فصل سوم |
| انرژی جنبشی | |
| کار انجام شده توسط نیروی ثابت | |
| قضیه کار و انرژی جنبشی | |
| انرژی پتانسیل گرانشی | |
| کار و انرژی پتانسیل | |
| پایستگی انرژی مکانیکی | |
| توان |
در ادامه، فرمولهای نوشته شده در جدول فوق را با حل مثال به صورت خلاصه توضیح میدهیم.
انرژی جنبشی چیست؟
به انرژی مرتبط با حرکت جسم، انرژی جنبشی گفته میشود. اجسام متحرک قادر به انجام تغییر یا انجام کار هستند. به عنوان مثال، تعدادی سنگ کوچک را روی یکدیگر میچینید و توپی را به سمت آنها پرتاب میکنید. توپ پس از پرتاب با سرعت مشخصی به سنگها برخورد میکنند و سبب جابجایی و بههمریختگی آنها میشود. انرژی جنبشی حرکتی از رابطه زیر به دست میآید:
m = جرم جسم
v = سرعت جسم در حال حرکت
همانطور که در رابطه فوق دیده میشود انرژی جنبشی هر جسم به جرم و سرعت حرکت آن وابسته است. هرچه جرم جسم بیشتر باشد یا با سرعت بیشتری حرکت کند، مقدار انرژی جنبشی آن نیز بیشتر خواهد بود.

کار انجام شده توسط نیروی ثابت
برای انجام کار، نیروی خارجی باید بر جسم وارد شود و جسم باید در راستای نیروی وارد شده جابجا شود. در نتیجه، برای بهدست آوردن کار نیاز به مولفه نیرو در راستای جابجایی داریم. تعریف کار به زبان ریاضی به صورت ضرب داخلی نیرو در جابجایی و به صورت زیر نوشته میشود:
رابطه بالا نشان میدهد که کار کمیتی اسکالر است و تنها اندازه دارد. برای رابطه فوق داریم:
- W برابر کار انجام شده توسط نیروی وارد شده است.
- F نیرویی است که بر جسم وارد میشود و آن را به اندازه مشخصی جابجا میکند.
- زاویه بین بردارهای نیرو و جابجایی است.
واحد SI کار، ژول است. یک ژول به صورت کار انجام شده توسط نیرویی برابر یک نیوتن برای جابجایی جسم به اندازه یک متر در راستای نیرو، تعریف میشود.
کار و انرژی جنبشی
قضیه کار و انرژی یکی از مهمترین فرمول های فیزیک دهم در فصل سوم است. هر جسمی برای حرکت به انرژی نیاز دارد. انتقال انرژی میتواند به شکل اعمال نیرو بر جسم باشد. همانطور که در بخش قبل دیدیم، به مقدار انرژی منتقل شده توسط نیرو به جسم برای به حرکت درآوردن آن، کار یا کار انجام شده میگوییم. بنابراین، کار و انرژی رابطه مستقیمی با یکدیگر دارند. در واقع، تفاوت بین انرژی جنبشی جسم، برابر کار انجام شده توسط آن است:
در رابطه فوق:
- W برابر کار انجام شده توسط جسم و بر حسب ژول است.
- m برابر جرم جسم و بر حسب کیلوگرم است.
- برابر سرعت اولیه جسم و بر حسب متر بر ثانیه اندازه گرفته میشود.
- برابر سرعت نهایی جسم و بر حسب متر بر ثانیه اندازه گرفته میشود.
در نتیجه، بر طبق قضیه کار و انرژی:
مقدار کل کار انجام شده توسط نیرو بر روی جسم برابر با تغییرات انرژی جنبشی آن است.
کار و انرژی پتانسیل
انرژی پتانسیل نیز همانند انرژی جنبشی با کار رابطه دارد. انرژی پتانسیل، U، برابر مقدار کاری است که برای جابجایی جسم از نقطه مرجع با انرژی پتانسیل صفر به نقطهای با موقعیت r، انجام میشود. نقطه مرجع یک نقطه دلخواه است، بنابراین با توجه به مساله داده شده انتخاب میشود.
کار انجام شده توسط انرژی پتانسیل گرانشی
جسمی به جرم m در حال سقوط است و دو نیروی وزن، mg، رو به پایین و مقاومت هوا، f، رو به بالا و در خلاف جهت حرکت جسم بر آن وارد میشوند. کار نیروی وزن وقتی از ارتفاع به ارتفاع میرسد برابر است با:
انرژی پتانسیل گرانشی را نیز میتوان به صورت زیر تعریف کرد:

پایستگی انرژی مکانیکی
مقدار انرژی موجود در جهان ثابت است. انرژی نه از بین میرود، نه به وجود میآید، بلکه از شکلی به شکل دیگر تبدیل میشود. انرژی مکانیکی هر جسم به صورت مجموع انرژی جنبشی و پتانسیل جسم تعریف و با E نشان داده میشود. انرژی مکانیکی جسمی در حال سقوط به طرف زمین در تمام نقاط مسیر، به خصوص نقطه شروع و پایان حرکت، حرکت یکسان است:
قانون پایستگی انرژی
مقدار انرژی در هر فرآیندی ثابت است. شکل آن ممکن است تغییر کند یا از سیستمی به سیستم دیگر منتقل شود، اما مقدار آن همواره ثابت خواهد بود. این جمله بیانگر یکی از مهمترین قانونهای موجود در فیزیک به نام قانون پایستگی انرژی یا قانون بقای انرژی است.
توان چیست؟
مدت زمان انجام کاری معین در فیزیک بسیار مهم است. توان متوسط در فیزیک به صورت مقدار کار انجام شده در زمانی مشخص تعریف میشود:
بازده چیست؟
هیچ سیستمی نمیتواند انرژی ورودی را به صورت کامل به کار مفید تبدیل کند و تنها بخشی از انرژی ورودی به سیستم به صورت کار مفید از آن خارج میشود. نسبت انرژی خروجی به انرژی ورودی، بازده نام دارد و برحسب درصد بیان میشود.
پس از آشنایی با مهمترین فرمولهای فیزیک دهم در فصل سوم، چند مثال را با یکدیگر حل میکنیم.
مثال کار و انرژی جنبشی
شخصیی توپی به جرم ۵۰۰ گرم را از روی زمین برمیدارد و آن را تا ارتفاع ۱۵۰ سانتیمتر بالا میبرد. سپس، توپ را از همان ارتفاع با تندی ۱۰ متر بر ثانیه پرتاب میکند. مقدار کار انجام شده توسط شخص روی توپ چه مقدار است؟
۷/۳۵ ژول
۳۲/۳۵ ژول
۲۵ ژول
۲۵/۳۵ ژول
برای حل هر مسئله فیزیکی ابتدا باید صورت مسئله را با دقت بخوانیم. در این مثال، شخصی توپی به جرم ۵۰۰ گرم را از روی زمین برمیدارد و آن را تا ارتفاع ۱۵۰ سانتیمتری بالا میبرد. سپس، توپ را با تندی ۱۰ متر بر ثانیه پرتاب میکند. کار انجام شده توسط شخص روی توپ را میخواهیم بهدست آوریم. برای محاسبه کار باید به این نکته توجه داشته باشیم که شخص در دو مرحله توپ را حرکت میدهد. بنابراین، کار هر مرحله را جداگانه بهدست میآوریم.
مقدار کار انجام شده توسط انرژی پتانسیل برابر است با:
اگر U برابر انرژی پتانسیل گرانشی باشد، مقدار کار انجام شده را میتوانیم به صورت زیر بنویسیم:
همچنین، مقدار کار انجام شده توسط انرژی جنبشی برابر است با:
مرحله اول حرکت
شخص ابتدا توپ را از روی زمین برمیدارد و آن را تا ارتفاع ۱۵۰ سانتیمتر بالا میبرد. به این نکته توجه داشته باشید که سرعت توپ در ابتدا و انتهای این حرکت برابر صفر است، بنابراین تغییر انرژی جنبشی توپ نیز برابر صفر خواهد بود. توپ از روی زمین تا ارتفاع ۱۵۰ سانتیمتر بالا برده میشود. کار انجام شده توسط نیروی وزن برابر است با:
اما ما میخواهیم مقدار کار انجام شده توسط شخص را محاسبه کنیم. کار انجام شده توسط شخص برابر است با:
برای محاسبه کار باید ارتفاع را برحسب متر و جرم را برحسب کیلوگرم در رابطه فوق قرار دهیم. جسم، ابتدا در ارتفاع صفر قرار دارد و شخص آن را تا ارتفاع ۱/۵ متری بالا میبرد:
مرحله دوم
در ادامه، شخص توپ را با تندی ۱۰ متر بر ثانیه پرتاب میکند. در این حالت، ارتفاع توپ تغییر نمیکند اما سرعت آن تغییر میکند. در نتیجه، کار انجام شده در مرحله دوم برابر تغییرات انرژی جنبشی توپ است:
در نتیجه، مقدار کل کار انجام شده توسط شخص روی توپ برابر است با:
مثال پایستگی انرژی مکانیکی
توپی فلزی به جرم دو کیلوگرم از طنابی آویزان شده است. این توپ مطابق تصویر نشان داده شده در ادامه از نقطه A رها میشود و تا نقطه B حرکت میکند. کدامیک از گزینههای زیر در مورد سرعت توپ صحیح است؟
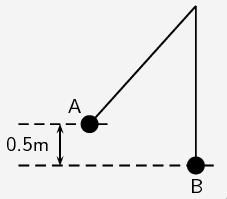
سرعت توپ در نقطه B برابر ۳/۱۳ متر بر ثانیه و مقدار آن مستقل از جرم توپ است.
سرعت توپ در نقطه B برابر ۹/۸ متر بر ثانیه و مقدار آن مستقل از جرم توپ است.
سرعت توپ در نقطه B برابر ۳/۱۳ متر بر ثانیه و مقدار آن وابسته به جرم توپ است.
سرعت توپ در نقطه B برابر ۵/۱۳ متر بر ثانیه و مقدار آن وابسته به جرم توپ است.
برای حل این مسئله گامهای زیر را به ترتیب طی میکنیم.
گام اول
مسئله داده شده را به دقت میخوانیم و مقدارهای معلوم را مشخص میکنیم:
- جرم توپ فلزی برابر ۲ کیلوگرم است.
- تغییر ارتفاع بین نقطه A و B برابر ۰/۵ متر است.
- توپ از نقطه A رها میشود، بنابراین سرعت آن در نقطه A برابر صفر متر بر ثانیه است.
گام دوم
مسئله را با استفاده از قانون پایستگی انرژی مکانیکی حل میکنیم. از آنجا که هیچ اصطکاکی وجود ندارد، انرژی مکانیکی پایسته است:
با حذف m از طرفین رابطه بالا، داریم:
مطابق رابطه بهدست آمده، سرعت توپ مستقل از جرم آن است. این بدان معنا است که هرگاه هر توپی با هر جرمی از ارتفاع یکسانی رها شود، سرعت آن در نقطه B یکسان خواهد بود.
گام سوم
سرعت توپ در نقطه B را میتوانیم با استفاده از رابطه بهدست آمده در گام دوم، محاسبه کنیم:
با جایگذاری مقدارهای داده شده در این رابطه، سرعت توپ در نقطه B را بهدست میآوریم:
مثال توان
سرعت اتومبیل خود را در مدت زمان ۱۰/۰ ثانیه از ۱۰ متر بر ثانیه به ۲۰ متر بر ثانیه میرسانید. اگر وزن شما و اتومبیل با یکدیگر برابر ۵۰۰ کیلوگرم باشد، مقدار توان استفاده شده چه مقدار است؟
مقدار توان با استفاده از رابطه زیر بهدست میآید:
مقدار زمان داده شده برابر ۱۰/۰ ثانیه است. برای محاسبه کار از تغییرات انرژی جنبشی اتومبیل استفاده میکنیم:
مقدار بهدست آمده برای کار را بر زمان انجام کار، ۱۰/۰ ثانیه، تقسیم میکنیم و توان را بهدست میآوریم:
$$P = \frac { 7.5 \times 10 ^ 4 } { 10.0 \ } = 7.5 \times 10 ^ 3 \ W$$
فرمول های فیزیک دهم فصل چهارم
در فصل چهارم از فیزیک دهم در مورد دما و گرما صحبت میشود. بنابراین، فرمول های فیزیک دهم در فصل چهارم در رابطه با مبحث گرما و دما هستند.
ابتدا فرمولهای این مبحث را به صورت خلاصه بیان، سپس چند مسئله را در این رابطه با یکدیگر حل میکنیم. فرمولهای فصل چهارم فیزیک دهم در جدول زیر به صورت خلاصه نوشته شدهاند.
| مبحث موردنظر | فرمول های فیزیک دهم فصل چهارم |
| تبدیل کلوین به سلسیوس | |
| تبدیل سلسیوس به کلوین | |
| تبدیل سلسیوس به فارنهایت | |
| تبدیل فارنهایت به سلسیوس | |
| انبساط خطی | |
| انبساط سطحی | |
| انبسط حجمی | |
| گرمای مبادله شده بین جسم و محیط | |
| رابطه بین ظرفیت گرمایی و ظرفیت گرمایی ویژه | |
| دمای تعادل | |
| گرماسنج و گرماسنجی | |
| گرمای نهان ذوب | |
| گرمای نهان تبخیر | |
| قانون شارل یا گاز در فشار ثابت | |
| قانون گیلوساک یا گاز در حجم ثابت | |
| قانون بویل یا گاز در دمای ثابت | |
| قانون آووگادرو | |
| قانون گاز کامل یا آرمانی |
در ادامه این مطلب از مجله فرادرس، فرمولهای نوشته شده در جدول فوق را با حل مثال به صورت خلاصه توضیح میدهیم.
دما و دماسنجی
در حالت کلی سه مقیاس دمایی وجود دارند:
- سلسیوس
- کلوین
- فارنهایت
این سه مقیاس را میتوان به یکدیگر تبدیل کرد. آسانترین تبدیل دمایی، از کلوین به درجه سلسیوس انجام میشود. اندازه دو واحد یکسان و فاصله دمایی یک کلوین برابر با یک درجه سلسیوس است. دمای صفر مطلق در مقیاس کلوین برابر و در مقیاس سلسیوس برابر است. بنابراین، برای تبدیل بین این دو مقیاس، عدد نیاز خواهد بود. در ادامه، تبدیل بین این دو مقیاس به زبان ریاضی را مشاهده میکنید:
تبدیل کلوین به سلسیوس
فرمول در زیر آورده شده است.
تبدیل سلسیوس به کلوین
فرمول در زیر آورده شده است.
درجه سلسیوس با استفاده از فرمول زیر به درجه فارنهایت تبدیل میشود:
درجه فارنهایت با استفاده از فرمول زیر به درجه سلسیوس تبدیل میشود:
انبساط گرمایی چیست؟
به طور حتم با این صحنه مواجه شدهاید، ظرفی را از داخل یخچال بیرون میآورید اما نمیتوانید در آن را به راحتی باز کنید. ظرف را مدت کوتاهی زیر آب گرم نگه میدارید و سپس در آن را به راحتی باز میکنید. چرا در شیشه مربا به راحتی باز میشود؟ زیرا با نگه داشتن ظرف مربا زیر آب گرم، حجم آن افزایش مییابد. حجم مواد و اجسام مختلف با افزایش دما، افزایش مییابد. به این عمل انبساط گرمایی گفته میشود.

انبساط خطی چیست؟
میلهای با طول اولیه و دمای اولیه داریم. با افزایش دمای میله تا مقدار ۷، طول آن نیز باید تا مقدار افزایش یابد. اگر تغییر دمای میله خیلی زیاد نباشد، تغییر طول آن، را میتوانیم با استفاده از رابطه زیر بهدست آوریم:
در رابطه فوق:
- ضریب انبساط طولی میله و یکای اندازهگیری آن یا است. مقدار ضریب انبساط طولی به جنس میله بستگی دارد.
- و به ترتیب تغییر طول و طول اولیه میله هستند و یکای اندازهگیری آنها متر است. این بدان معنا است که طول برحسب سانتیمتر یا میلیمتر باید به متر تبدل شوند.
- تغییر دما و یکای اندازهگیری آن کلوین یا درجه سلسیوس است.
انبساط سطحی چیست؟
جسمی با مساحت اولیه و دمای اولیه داریم. با افزایش دمای جسم تا مقدار ، مساحت آن نیز باید تا مقدار افزایش یابد. تغییر مساحت جسم، را میتوانیم با استفاده از رابطه زیر بهدست آوریم:
در رابطه فوق:
- ضریب انبساط طولی جسم و یکای اندازهگیری آن یا است.
- و به ترتیب تغییر مساحت و مساحت اولیه جسم هستند و یکای اندازهگیری آنها مترمربع است.
- تغییر دما و یکای اندازهگیری آن کلوین یا درجه سلسیوس است.

انبساط حجمی چیست؟
جسمی با حجم اولیه و دمای اولیه داریم. با افزایش دمای جسم تا مقدار ۷، حجم آن نیز باید تا مقدار افزایش یابد. تغییر حجم جسم، را میتوانیم با استفاده از رابطه زیر بهدست آوریم:
در رابطه فوق، ضریب انبساط حجمی جسم است. افزایش حجم بیشتر مواد جامد به هنگام افزایش دما در تمام راستاها به صورت یکسان انجام میشود. بنابراین، در حالت کلی ضریب انبساط حجمی، ، سه برابر ضریب انبساط طولی، ، است:
ظرفیت گرمایی چیست؟
به مقدار انرژی گرمای لازم برای افزایش دمای جسمی مشخص به اندازه یک درجه سلسیوس، ظرفیت گرمایی گفته میشود. به مقدار انرژی گرمایی لازم برای افزایش دمای یک گرم از مادهای مشخص به اندازه یک درجه سلسیوس، گرمای ویژه گفته میشود. گرمای ویژه با c و ظرفیت گرمایی با C نشان داده میشوند. واحد اندازهگیری گرمای ویژه برابر یا است. جسم دلخواهی را در نظر بگیرید که با محیط اطراف خود مقداری گرما به اندازه Q مبادله و به همین دلیل دمای جسم از مقدار به تغییر میکند. مقدار گرمای مبادله شده بین جسم و محیط اطراف آن با تغییرات دمای جسم متناسب است و به صورت زیر نوشته میشود:
C ظرفیت گرمایی جسم است و به جنس و جرم جسم بستگی دارد. ظرفیت گرمایی با استفاده از رابطه زیر به گرمای ویژه مربوط میشود:
رابطه فوق را در رابطه قرار میدهیم. بنابراین، گرمای مبادله شده بین جسم و محیط به صورت زیر نوشته میشود:
گرمای ویژه هر جسمی به جنس ماده سازنده جسم و دمای آن بستگی دارد.
دمای تعادل
فرض کنید تعدادی جسم با جرمهای و و و ...، گرماهای ویژه و و و ... و دماهای اولیه و و و ... در تماس با یکدیگر قرار دارند. دماهای این اجسام پس از مدتی با یکدیگر برابر میشوند. دمای تعادل، ، را میتوانیم با استفاده را از رابطه زیر بهدست آوریم:
گرماسنج و گرماسنجی
گرماسنج (کالریمتر) ظرفی است که به خوبی از نظر گرمایی عایقبندی شده است و از آن برای اندازهگیری گرمای ویژه اجسام مختلف استفاده میشود. مقداری آب با جرم معین داخل گرماسنج میریزیم. پس از رسیدن آب و گرماسنج به دمایی یکسان، دمای آب را اندازه میگیریم. جسمی با جرم و دمای اولیه مشخص را درون گرماسنج قرار میدهیم. برای آنکه مجموعه گرماسنج، آب و جسم زودتر به دمای تعادل برسد، آب را هم میزنیم. پس از رسیدن مجموعه به دمای تعادل، مقدار آن را به صورت زیر محاسبه میکنیم:
تبدیل حالت جامد به مایع
فرایندی که در آن ماده جامد با اضافه کردن گرما به مایع تبدیل میشود، ذوب نام دارد. به دمایی که در آن ماده جامد با گرفتن گرما به مایع تبدیل میشود، نقطه ذوب میگوییم. این اتفاق در فشار یک اتمسفر رخ میدهد. در نقطه ذوب، دو فاز مایع و جامد در حالت تعادل در کنار یکدیگر قرار دارند. به مقدار گرمای لازم بر حسب ژول برای تبدیل جامد به مایع در نقطه ذوب و در دمای ثابت، گرمای نهان ذوب گفته میشود. گرمای نهان ذوب برابر مقدار انرژی لازم برای تبدیل ماده از حالت جامد به مایع در دمای ثابت است و با استفاده از فرمول زیر بهدست میآید:

در رابطه فوق:
- برابر مقدار انرژی جذب شده برای تبدیل ماده از مایع به جامد است و بر حسب ژول یا کالری اندازه گرفته میشود.
- جرم است و بر حسب کیلوگرم اندازه گرفته میشود.
- گرمای ویژه نهان ذوب است.
توجه به این نکته مهم است که اگر تغییر فاز مایع به جامد انجام شود، ماده گرما از دست خواهد داد و مقدار گرمای از دست داده برابر است با:
تبدیل حالت مایع به گاز
اگر آب را به اندازه کافی گرم کنیم، شروع به جوشیدن میکند. به فرایندی که طی آن مایع میجوشد و به گاز تبدیل میشود، تبخیر میگوییم. گرمای نهان تبخیر برابر مقدار انرژی لازم برای تبدیل ماده از حالت مایع به گاز در دمای ثابت است و از حاصلضرب جرم جسم در گرمای نهان تبخیر بهدست میآید:

در رابطه فوق:
- برابر مقدار انرژی جذب شده برای تبدیل ماده از مایع به بخار است و بر حسب ژول یا کالری اندازه گرفته میشود.
- جرم است و بر حسب کیلوگرم اندازه گرفته میشود.
- گرمای ویژه نهان تبخیر است.
توجه به این نکته مهم است که اگر تغییر فاز گاز به مایع انجام شود، ماده گرما از دست خواهد داد و مقدار گرمای از دست داده برابر است با:
قوانین گازها
در فشار ثابت و در شرایطی که جرم ثابت است، حجم گاز به طور مستقیم با دما متناسب است:
به این نکته توجه داشته باشد که در رابطه فوق، دما برحسب کلوین نوشته میشود. همچنین، در حجم و جرم ثابتِ گازی مشخص، فشار گاز به صورت مستقیم با دما متناسب است.
قانون بویل رابطه بین حجم و فشار گاز را در دما و جرمِ ثابت، توضیح میدهد. بر طبق این قانون، با ثابت نگه داشتن دمای گاز، حجم آن با افزایش فشار، کاهش خواهد یافت. به بیان دیگر، با ثابت نگه داشتن دمای گاز، حجم به صورت معکوس با فشار تغییر میکند. به این نکته توجه داشته باشید که در این حالت، تعداد مولکولهای گاز نیز باید ثابت باشند:
قانون گازهای کامل (آرمانی)
قانونهای بیان شده برای گازها، برای گاز کامل یا آرمانی با دقت خوبی برقرار است. گازی کامل است که مشخصات زیر را داشته باشد:
- به اندازه کافی رقیق یا چگالی آن بسیار کوچک باشد.
- مولکولهای تشکیلدهنده گاز هیچ برهمکنشی با یکدیگر ندارند.
رابطههای بخش قبل را میتوانیم به شکلی کلی به نام قانون گازهای آرمانی و به صورت زیر بنویسیم:
مقدار ثابت را با R نشان میدهیم. R ثابت جهانی گازها نام دارد و مقدار آن برابر است. در نتیجه، قانون گازهای کامل به صورت زیر نوشته میشود:
مثال گرمای ویژه
دو قطعه یخ با دمای صفر درجه سلسیوس داخل ظرفِ آبی با دمای ۲۵ درجه سلسیوس قرار داده میشوند. در نتیجه، دمای آب داخل ظرف تا یک درجه سلسیوس کاهش مییابد و قطعههای یخ به طور کامل آب میشوند. اگر پس از ذوب کامل دو قطعه یخ، دو قطعه یخِ دیگر با دمای صفر درجه سلسیوس را داخل ظرف آب قرار دهیم، چه اتفاقی رخ میداد؟
یخها آب و دمای آبِ داخل ظرف به صفر درجه سلسیوس میرسد.
یخها آب و دمای آبِ داخل ظرف بالاتر از صفر درجه سلسیوس میشود.
مقداری یخ با دمای صفر درجه و آب با دمای بالاتر از صفر درجه داخل ظرف باقی میماند.
مخلوط یخ و آب با دمای سفر درجه سلسیوس داخل ظرف باقی میماند.
حل این مثال به محاسبات ریاضی و نوشتن فرمول نیاز ندارد. تنها با آشنایی با مفاهیم گرمای ویژه و گرمای نهان میتوانیم این مثال را حل کنیم. در حالت اول، دو قطعه یخ داخل ظرف آب با دمای ۲۵ درجه سلسیوس انداخته میشوند. از آنجا که گرما از جسمی با دمای بیشتر به جسمی با دمای کمتر منتقل میشود، گرما از آب با دمای ۲۵ درجه سلسیوس به قطعههای یخ با دمای صفر درجه سلسیوس منتقل میشود. در نتیجه، تمام یخها ذوب و دمای آب به یک درجه سلسیوس کاهش مییابد. در ادامه، دو قطعه یخ با دمای صفر درجه سلسیوس را داخل ظرف آب با دمای یک درجه سلسیوس قرار میدهیم.
باز هم گرما از آب با دمای یک درجه سلسیوس به یخها منتقل میشود. انتقال گرما تا جایی ادامه مییابد که دمای آب به صفر درجه سلسیوس برسد. طی این فرآیند، مقداری از یخها ذوب میشوند. برای ذوب کامل دو قطعه یخ، اضافه شده باید دمای آب، داخل ظرف ۲۴ درجه سلسیوس کاهش یابد. بنابراین، در پایان مقداری یخ داخل ظرفِ آب باقی میماند و در پایان مخلوطی از آب و یخ با دمای صفر درجه سلسیوس داریم.

مثال محاسبه گرمای ویژه و گرمای نهان
قطعه یخی به جرم ۲/۵ کیلوگرم در دمای ۱۵- درجه سلسیوس داریم. مقدار گرمای لازم برای تبدیل این یخ به آبِ ۳۵ درجه سلسیوس چه مقدار است؟ (ظرفیت گرمایی ویژه یخ برابر ، ظرفیت گرمایی ویژه آب برابر و گرمای نهان ذوب یخ برابر است. )

۱۲۷۷/۵۲۵ کیلوژول
۱۳۷۷/۵۲۵ کیلوژول
۱۲۰۰ کیلوژول
۱۱۹۹ کیلوژول
قطعهای یخ، ۲۵ کیلوگرمی با دمای ۱۵- درجه سلسیوس داریم. برای تبدیل این قطعه یخ به آبِ ۳۵ درجه سلسیوس باید مرحلههای زیر طی شوند:
- ابتدا دمای یخ تا صفر درجه سلسیوس افزایش یابد.
- با ثابت ماندن دما در صفر درجه سلسیوس، تمام یخ به آبِ صفر درجه سلسیوس تبدیل شود.
- دمای آب تا ۳۵ درجه سلسیوس افزایش یابد.
مرحله یک
دمای یخ به جرم ۲/۵ کیلوگرم از ۱۵- درجه سلسیوس تا صفر درجه سلسیوس افزایش مییابد. مقدار گرمای لازم برای انجام این کار عبارت است از:
مرحله دو
پس از آنکه دمای یخ به صفر درجه سلسیوس افزایش داد، گرمای بیشتری به آن میدهیم. در این حالت یخ، بدون تغییر دما، از حالت جامد به مایع تبدیل میشود. مقدار گرمای لازم برای انجام این کار عبارت است از:
مرحله سه
دمای آب به جرم ۲/۵ کیلوگرم از صفر درجه سلسیوس تا ۳۵ درجه سلسیوس افزایش مییابد. مقدار گرمای لازم برای انجام این کار عبارت است از:
در نتیجه، مقدار گرمای کل برای تبدیل یخی به جرم ۲/۵ کیلوگرم و دمای ۱۵- درجه سلسیوس به آبِ ۳۵ درجه سلسیوس برابر است با:
مثال قوانین گازها
۲/۰۳۵ گرم هیدروژن () فشاری برابر ۱/۰۱۵ اتمسفر در محفظهای به حجم ۵/۰۰ لیتر در دمای ۲۱۱/۷۶- درجه سلسیوس ایجاد میکند. اگر مقدار دیگر هیدروژن به جرم ۲/۰۹۹ گرم به محفظه اضافه کنیم، فشار تا مقدار ۳/۰۱۵ اتمسفر افزایش مییابد. مقدار دما پس از افزایش هیدروزن به محفظه بر حسب سلسیوس برابر است با:
۸۹/۵۵ درجه سلسیوس
۱۸۳/۶ درجه سلسیوس
۱۸۳/۶- درجه سلسیوس
سفر درجه سلسیوس
برای حل این مثال گامهای زیر را طی میکنیم.
گام اول
برای حل این مثال از چه قانون گازی باید استفاده کنیم؟ مقدارهای حجم، دما و فشار اولیه، قبل از اضافه کردن هیدروژن به محفظه، داده شدهاند. همچنین، جرم و وزن مولکولی به ما تعداد مولها را میدهد. بنابراین، اینگونه به نظر میرسد که با استفاده از قانون گاز کامل میتوانیم این مسئله را حل کنیم. اما شرایط گاز در محفظه با افزودن مقداری هیدروژن به آن تغییر میکند. از اینرو، باید به شرایط اولیه و نهایی توجه داشته باشیم.
گام دوم
قانون گاز کامل به صورت زیر نوشته میشود:
رابطه فوق در حالت اولیه برابر و پس از افزودن هیدروژن به محفظه به صورت نوشته میشود.
گام سوم
R در هر دو معادله و ثابت است، بنابراین مقدار آن را میتوانیم به صورت زیر بنویسیم:
از آنجا که R ثابت جهانی گازها است و مقدار آن با تغییر شرایط، تغییر نمیکند، سمت راست دو معادله بالا با یکدیگر برابر هستند:
گام چهارم
گاز هیدروژن به محفظهای با حجم ثابت اضافه میشود، بنابراین حجم محفظه، قبل و بعد از اضافه کردن هیدروژن به آن ثابت میماند. از اینرو، میتوان و را از طرفین رابطه بالا حذف کرد:
گام پنجم
پس از افزودن هیدروژن به محفظه میخواهیم بدانیم دمای آن چه مقدار میشود. بنابراین، رابطه را برحسب دمای ثانویه یا مینویسیم:
گام ششم
برای محاسبه تعداد مولِ گاز هیدروژن، باید مقدار آن برحسب گرم را بر جرم مولی آن تقسیم کنیم.
این رابطه را در رابطه قرار میدهیم:
با حذف M از رابطه فوق به رابطه نهایی زیر میرسیم:
گام هفتم
مقدارهای اولیه و نهایی فشار، جرم اولیه و نهایی و دمای اولیه را در رابطه نهایی قرار میدهیم و دمای گاز را پس از افزودن گاز هیدروژن به محفظه بهدست میآوریم:
توجه به این نکته مهم است که دمای اولیه در رابطه بالا برحسب کلوین نوشته شده است، همچنین، مقدار برابر مجموع مقدار اولیه هیدروژن در محفظه و مقدار اضافه شده است. دمای ۸۹/۵۵ کلوین برحسب سلسیوس برابر است با:
فرمول های فیزیک دهم فصل پنجم
فرمول های فیزیک دهم در فصل پنجم از فیزیک دهم، رشته ریاضیفیزیک، در مورد قانون اول ترمودینامیک، برخی از فرایندهای ترمودینامیکی، چرخه ترمودینامیکی، ماشینهای گرمایی و قانون دوم ترمودینامیک به بیان ماشین گرمایی هستند. ابتدا فرمولهای این مبحث را به صورت خلاصه بیان، سپس چند مسئله را در این رابطه با یکدیگر حل میکنیم. فرمولهای فصل پنجم فیزیک دهم در جدول زیر به صورت خلاصه نوشته شدهاند.
| مبحث موردنظر | فرمول های فیزیک دهم فصل پنجم |
| قانون اول ترمودینامیک | |
| فرایند همحجم |
|
| فرایند همفشار |
|
| فرایند همدما | |
| فرایند بیدرو یا آدیاباتیک | |
| فرایند چرخهای | |
| بازده ماشین گرمایی |
در ادامه، فرمولهای نوشته شده در جدول فوق را با حل مثال به صورت خلاصه توضیح میدهیم.
قانون اول ترمودینامیک
قانون اول ترمودینامیک با انرژی درونی، گرما و کار ارتباط دارد. این قانون، بیان دیگری از اصل پایستگی انرژی است. بر طبق این اصل، انرژی نه به وجود میآید، نه از بین میرود، بلکه از حالتی به حالت دیگر تبدیل یا از مکانی به مکان دیگر منتقل میشود. انرژی از دو طریق کار و گرما میتواند به سیستم وارد یا از آن خارج شود. تغییرات انرژی درونی یکی از مهمترین فرمولهای فیزیک دهم در بخش ترمودینامیک است. تغییرات انرژی درونی سیستمی مشخص را میتوانیم با استفاده از رابطه زیر بهدست آوریم:
به هنگام حل مسائل مربوط به تغییر انرژی درونی سیستم باید به نکتههای زیر توجه داشته باشیم:
- کار انجام شده توسط سیستم روی محیط، منفی در نظر گرفته میشود. سیستم برای انجام کار باید انرژی مصرف کند. بنابراین، انرژی درونی آن کاهش مییابد.
- در مقابل، کار انجام شده روی سیستم توسط محیط اطراف آن، مثبت در نظر گرفته میشود.
- اگر گرما به سیستم وارد شود، گرما را مثبت و اگر گرما از سیستم خارج شود، آن را منفی در نظر میگیریم.
انواع فرایندهای ترمودینامیکی
فرایندهای ترمودینامیکی در ترمودینامیک فیزیک دهم به چهار دسته تقسیم میشوند. هر دسته ویژگیهای منحصر به خود را دارد.
فرایند هم حجم
در این فرایند، حجم سیستم ثابت و در نتیجه کار انجام شده برابر صفر خواهد بود:
از آنجا که کار انجام شده توسط سیستم در این فرایند برابر صفر است، تغییرات گرما برابر تغییرات انرژی درونی سیستم خواهد بود:
فرایند هم فشار یا ایزوبار
فرایند همفشار، فرایندی ترمودینامیکی است که در فشار ثابت رخ میدهد. فشار ثابت هنگامی بهدست میآید که حجم منبسط یا منقبض میشود. به این ترتیب، هر تغییر فشاری به دلیل انتقال گرما، خنثی خواهد شد.
کار انجام شده در فرایند همفشار با استفاده از رابطه زیر بهدست میآید:
اگر گاز منبسط شود، حجم نهایی بزرگتر از حجم اولیه و کار انجام شده توسط گاز منفی است. اگر گاز فشرده شود، حجم نهایی کوچکتر از حجم اولیه و کار انجام شده توسط گاز مثبت خواهد بود.
فرایند هم دما
فرایند همدما، فرایندی ترمودینامیکی است که در دمای ثابت رخ میدهد. در این فرایند، انتقال گرما به سیستم یا خروج گرما از آن به اندازهای آهسته انجام میشود که تعادل گرمایی برقرار باشد. این فرایند میتواند هنگامی رخ دهد که سیستم با منبع گرمایی خارجی در تماس باشد. از آنجا که انرژی درونی گاز ایدهال، تنها به دما وابسته و در فرایند همدما، دمای سیستم بدون تغییر باقی میماند، تغییر انرژی درونی برابر صفر خواهد بود:
نکته: در تراکم یا انبساط گاز، کار انجام شده توسط محیط روی گاز، مثبت است، بنابراین Q منفی خواهد شد.
فرایند بی درو یا آدیاباتیک
در این فرایند، هیچ گرمایی به سیستم وارد یا از آن خارج نمیشود. توجه به این نکته مهم است که در فرایند بیدررو، تبادل گرمایی به هنگام انبساط یا انقباض سیستم، برابر صفر خواهد بود. از آنجا که در فرایند بیدررو هیچ گرمایی از سیستم خارج یا به آن وارد نمیشود، Q برابر صفر خواهد بود:
نکته: اگر گاز ایدهال به صورت بیدررو منبسط شود، کار محیط روی سیستم (گاز) منفی است. از اینرو، تغییرات انرژی درونی گاز منفی است و دمای آن کاهش مییابد. در مقابل، اگر گاز ایدهال به صورت بیدررو متراکم یا منقبض شود، تغییرات انرژی درونی آن مثبت است و دمای گاز افزایش خواهد یافت.
فرایند چرخه ای در ترمودینامیک چیست؟
در فرایندهای چرخهای، حالت اولیه سیستم با حالت نهایی آن برابر است. در این حالت تغییرات انرژی درونی، یعنی برابر صفر خواهد بود. در نتیجه، بر طبق قانون اول ترمودینامیک داریم:
بازده ماشین گرمایی
دیدگاه ایدهال در هر ماشین گرمایی آن است که انرژی ورودی به آن تا حد امکان به انرژی مفید یا کار تبدیل شود. بازده هر ماشین گرمایی به صورت نسبت انرژی مفید خروجی به انرژی داده شده به ماشین تعریف میشود:
انرژی ورودی به ماشین گرمایی همان گرمای داده شده به ماشین، ، و انرژی مفید خروجی، همان کار انجام شده توسط ماشین است:
قانون دوم ترمودینامیک به بیان ماشین گرمایی
تقریبا همه ماشینهای گرمایی با دو منبع گرمایی با دو دمای متفاوت کار میکنند. منبع گرمایی با دمای بالاتر با و منبع گرمایی با دمای پایینتر با نشان داده میشوند. مقداری از گرمای گرفته شده از منبع به کار تبدیل و مابقی آن به منبع گرمایی با دمای پایینتر داده میشود.
قانون دوم ترمودینامیک و یخچال ها در فرمول های فیزیک دهم
گرما نمیتواند به صورت خودبهخودی از جسم سرد به جسم گرم منتقل شود. این عبارت بیان یخچالی قانون دوم ترمودینامیک نام دارد. با انجام کار، میتوان گرما را از جسمی با دمای پایینتر به جسمی با دمای بالاتر منتقل کرد. این کار توسط وسیلهای به نام یخچال انجام میشود.
مثال فرایند ترمودینامیکی
نمودار فشار برحسب حجم در تصویر زیر، دو فرایند همدما در دماهای متفاوت و را نشان میدهد. کدامیک از گزینههای زیر صحیح است؟
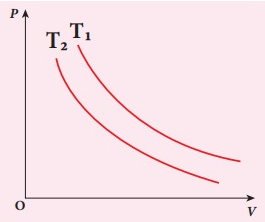
دمای بزرگتر از دمای است.
دمای بزرگتر از دمای است.
هیچکدام
برای آنکه بدانیم دمای کدام نمودار بالاتر است، خطی موازی محور افقی، محور حجم، به صورت نشان داده شده در تصویر زیر رسم میکنیم. این خط نمودار عمودی را در فشاری مشخص و یکسان قطع میکند. به بیان دیگر، فشار در تمام نقاط قرار گرفته روی خط افقی، یکسان است. خط افقی نمودارِ همدما با دمای را در نقطه A و نمودار همدما با دمای را در نقطه B قطع میکند. حجم در نقطههای A و B به ترتیب برابر و است.
در فشار ثابت، هرچه حجم گاز بیشتر باشد، دمای آن نیز بیشتر خواهد بود. با توجه به نمودار، حجم بزرگتر از حجم است. در نتیجه، دمای نیز بزرگتر از دمای خواهد بود.
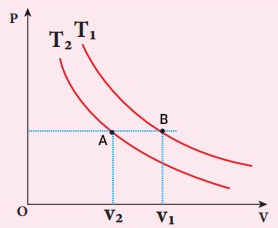
نکته: در حالت کلی، هرچه نمودار همدما به مبدأ نزدیکتر باشد، دمای آن کوچکتر است.
مثال چرخه ترمودینامیکی
بیشینه بازده ماشین گرمایی که بین دو دمای ۳۰۰ و ۵۰۰ درجه سلسیوس کار میکند، چه مقدار است؟
۲۶ درصد
۳۶ درصد
۵۶ درصد
۱۶ درصد
انرژی ورودی به ماشین گرمایی کارنو، همان گرمای داده شده به ماشین، ، و انرژی مفید خروجی، همان کار انجام شده توسط ماشین است:
رابطه فوق را میتوانیم به صورت نیز بنویسیم. بر طبق صورت مسئله، ماشین گرمایی کارنو بین دو دمای ۳۰۰ و ۵۰۰ درجه سلسیوس کار میکند. برای محاسبه بازده بیشینه این ماشین، باید دماهای داده شده را به کلوین تبدیل کنیم:
بازده ماشین کارنو برابر است با:
بنابراین، بیشینه بازده این ماشین کارنو برابر ۲۶ درصد است.
جمعبندی
در این مطلب از مجله فرادرس، با فرمول های فیزیک دهم آشنا شدیم. فیزیک دهم در رشتههای تجربی و ریاضیفیزیک به ترتیب از چهار و پنج فصل تشکیل شده است. فرمولهای هر فصل ابتدا به صورت خلاصه توضیح داده و در ادامه، برای درک بهتر فرمولها، تعدادی مسئله مرتبط با آنها حل شد.













واقعا عالی مفید و به درد بخور بود کل فیزیک دهم 150 صفحه ای رو در ۲۰ صفحه جمع کرده مرسی از سازنده این سایت ❤️
با تشکر از زحمات شما، مثال اول تبدیل واحدها اشتباه است. هیکدام از 4 جواب درست نیست و هم در حل مثال اشتباهشده است
با سلام خدمت شما؛
نکته بیان شده صحیح است و اصلاحات انجام شد.
با تشکر از همراهی شما با مجله فرادرس
هفتم اژه ای دو اصفهان هستم
نصف این مطالب تدریس شده به ما