گرمای ویژه (Specific Heat) – به زبان ساده

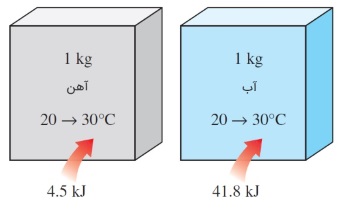
همه ما از روی تجربه میدانیم که مقدار گرمای لازم برای افزایش دمای مادههای مختلف، یکسان نیست. به عنوان مثال، برای اینکه دمای یک کیلوگرم آهن از $$\large 20 \:^\circ C$$ به $$\large 30 \:^\circ C$$ تغییر کند، به $$\large 4.5 \:kJ$$ انرژی نیاز است. ولی اگر بخواهیم دمای یک کیلوگرم آب را به همین اندازه افزایش دهیم، به گرمایی در حدود نُه برابر بیشتر ($$\large 41.8 \:kJ$$) نیاز خواهیم داشت. بنابراین، نیاز به پارامتری وجود دارد که ضمن توضیح دلیل این تفاوت، ما را قادر سازد تا مقدار انرژی ذخیره شده در مادههای گوناگون را با هم مقایسه کنیم. در این مقاله، مفهوم گرمای ویژه (Specific Heat) را بررسی خواهیم کرد.
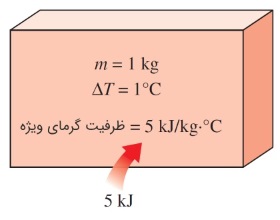
گرمای ویژه به صورت «انرژی مورد نیاز برای افزایش دمای یک کیلوگرم از یک ماده به اندازه یک درجه»، تعریف میشود. در حالت کلی، مقدار این انرژی به چگونگی انجام فرآیند بستگی دارد. در علم ترمودینامیک، دو نوع گرمای ویژه، مورد توجه است: یکی گرمای ویژه در حجم ثابت ($$\large c_v$$) و دیگری گرمای ویژه در فشار ثابت ($$\large c_p$$).
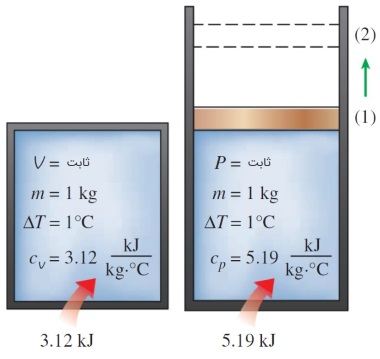
از نطر فیزیکی، گرمای ویژه در حجم ثابت به عنوان «انرژی مورد نیاز برای افزایش دمای یک کیلوگرم از یک ماده به اندازه یک درجه در شرایطی که حجم ثابت مانده باشد» تعریف میشود. در سوی مقابل، «انرژی مورد نیاز برای افزایش دمای یک کیلوگرم از یک ماده به اندازه یک درجه در شرایطی که فشار ثابت مانده باشد» گرمای ویژه در فشار ثابت مینامیم. این دو تعریف را میتوانید در شکل زیر برای یک ماده فرضی مشاهده کنید. گرمای ویژه در فشار ثابت، همواره از گرمای ویژه در حجم ثابت بزرگتر است. زیرا در فشار ثابت، سیستم تمایل دارد منبسط شود. به همین دلیل، انرژی مورد نیاز برای انبساط نیز باید به سیستم وارد شود.
اکنون باید بتوانیم ظرفیت گرمایی ویژه را برحسب سایر پارامترهای ترمودینامیکی بیان کنیم. جرم ثابتی را در یک سیستم بسته و ایستا در نظر بگیرید. این سیستم، تحت یک فرآیند حجم ثابت قرار میگیرد. در نتیجه، هیچگونه کارِ انبساط یا تراکم در این سیستم رخ نمیدهد. قانون پایستگی انرژی را در این فرآیند برای یک جزء دیفرانسیلی مینویسیم.
$$\large e_{in} \:-\: e_{out} \:=\: \Delta e_{system} \\~\\
\large \delta e_{in} \:-\: \delta e_{out} \:=\: \text{d}u$$
سمت چپ رابطه بالا، مقدار خالص انرژی مبادله شده با سیستم را نشان میدهد. با استفاده از تعریف $$\large c_v$$، این انرژی باید برابر با $$\large c_v \text{d} T$$ باشد. تغییر دیفرانسیلی دما را با $$\large \text{d} T$$ نشان دادهایم. بنابراین رابطه زیر برقرار است. $$\large c_v$$ برابر است با تغییر انرژی درونی با دما در حجم ثابت.
$$\large c_v \text{d} T \:=\: \text{d} u \\~\\
\large \Rightarrow ~~~ c_v \:=\: (\frac{\partial u}{\partial T})_v$$
(رابطه ۱)
به طور مشابه، رابطه ظرفیت گرمایی ویژه در فشار ثابت هم به صورت زیر تعریف میشود. در اینجا، انبساط و تراکم در فشار ثابت اتفاق میافتد. تغییر آنتالپی با دما را در فشار ثابت، $$\large c_p$$ مینامیم.
$$\large c_p \:=\: (\frac{\partial h}{\partial T})_p$$
(رابطه ۲)
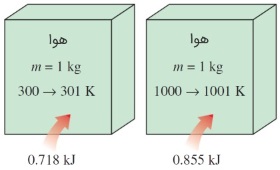
مانند سایر ویژگیهای ترمودینامیکی، $$\large c_v$$ و $$\large c_p$$ نیز به حالت ماده وابسته است. همانطور که میدانید، حالت ماده را در هر لحظه میتوان با استفاده از دو ویژگی شدتی (Intensive Property) و مستقل تعیین کرد. به همین دلیل، گرمای ویژه یک ماده در دماهای مختلف، مقادیر متفاوتی دارد.
با دقت در رابطههای ۱ و ۲ میتوانیم دو مورد مهم را نتیجهگیری کنیم:
- این دو رابطه بین ویژگیهای ترمودینامیکی ماده برقرار است. به همین دلیل مقدار آنها، مستقل از نوع فرآیند بوده و در هر فرآیندی معتبر است.
- نکته دیگری که باید به آن توجه کرد این است که $$\large c_v$$ به تغییرات انرژی درونی و $$\large c_p$$ به تغییرات آنتالپی مرتبط است. به عبارت دیگر، این دو پارامتر را میتوان به شکلی دیگر نیز تعریف کرد. گرمای ویژه در حجم ثابت، به صورت تغییر انرژی درونی یک ماده به ازای تغییر یک درجهای دما در حجم ثابت تعریف میشود. در سوی دیگر، گرمای ویژه در فشار ثابت نیز برابر با تغییر آنتالپی یک ماده به ازای تغییر یک درجهای دما در فشار ثابت است. بنابراین، تغییر انرژی درونی با دما، مقدار $$\large c_v$$ را عوض میکند ولی برای تغییر مقدار $$\large c_p$$، آنتالپی باید عوض شود.
با انتقال انرژی، میتوان انرژی درونی و آنتالپی یک ماده را تغییر داد؛ که انتقال گرما فقط یکی از انواع آن است. در نتیجه، در نگاه جامعتر شاید بهتر باشد به جای «گرمای ویژه» از عبارت «انرژی ویژه» استفاده شود.
یکی از واحدهای رایج برای اندازهگیری گرمای ویژه $$\large kJ/kg .^\circ C$$ یا $$\large kJ/kg .K$$ است. دقت کنید که این دو واحد تفاوتی با یکدیگر ندارند؛ زیرا $$\large \Delta T (^\circ C)$$ و $$\large \Delta T (K)$$ با هم برابرند. تغییر $$\large 1^\circ C$$ در دما، معادل تغییر $$\large 1K$$ است. در برخی مسائل هم گرماهای ویژه را با واحد $$\large kJ/kmol .^\circ C$$ یا $$\large kJ/kmol .K$$ بیان میکنند. در این حالت، گرمای ویژه در حجم ثابت و گرمای ویژه در فشار ثابت در مبنای مول و به ترتیب به صورت $$\large \bar{c }_v$$ و $$\large \bar{c }_p$$ نوشته میشوند.
گرمای ویژه در گازهای ایدهآل
قبلاً در مقالههایی از مجله فرادرس، در بحثهایی پیرامون ترمودینامیک و آنتالپی، رابطه زیر را برای گازهای ایدهآل تعریف کردیم. اکنون برای اینکه بتوانیم ارتباطی بین $$\large c_v$$ و $$\large c_p$$ پیدا کنیم، باید از رابطه زیر مشتق بگیریم.
$$\large h \:=\: u \:+\: RT \\~\\
\large \text{d}h \:=\: \text{d}u \:+\: R\text {d}T$$
اکنون به جای $$\large \text{d}h$$ و $$\large \text{d}u$$ به ترتیب، $$\large c_p\text{d}T$$ و $$\large c_v\text{d}T$$ را قرار داده و طرفین عبارت را به $$\large \text{d}T$$ تقسیم میکنیم.
$$\large c_p \:=\: c_v \:+\: R\: ~~~ ~~~ (kJ/kg.K)$$
این رابطه در گازهای ایدهآل از اهمیت بالایی برخوردار است. چرا که این امکان را میدهد تا با داشتن $$\large R$$ و یکی از گرماهای ویژه، دیگری را محاسبه کنیم. اگر گرماهای ویژه برحسب مول اندازهگیری شده باشند، باید به جای $$\large R$$ در رابطه بالا از ثابت جهانی گازها یعنی $$\large R_u$$ استفاده کنیم.
$$\large \bar{c}_p \:+\: \bar{c}_v \:+\: R_u\: ~~~ ~~~ (kJ/kmol.K)$$
پارامتر مهم دیگر در بحث گازهای ایدهآل، نسبت گرمای ویژه نامیده شده و به شیوه زیر تعریف میشود.
$$\large k \:=\: \frac {c_p} {c_v}$$
نسبت گرمای ویژه با دما تغییر میکند ولی تغییرات آن بسیار ناچیز است. در مورد گازهای تکاتمی، این نسبت ثابت و همیشه برابر با $$\large 1.667$$ است. در مورد گازهای دواتمی مانند هوا نیز این نسبت با تقریب خوبی برابر $$\large 1.4$$ است.
گرمای ویژه در مادههای جامد و مایع
مادهای که حجم مخصوص (یا چگالی) آن ثابت باشد را ماده تراکم ناپذیر مینامیم. حجم مخصوص جامدات و مایعات، در فرآیندهای مختلف، تقریباً ثابت میماند. بنابراین، این دو فاز ماده را میتوان با تقریب خوبی در گروه مادههای تراکم ناپذیر دستهبندی کرد. به عبارت دیگر وقتی مادهای که در فاز مایع یا جامد است، تحت یک فرآیند قرار بگیرد، انرژی مربوط به تغییر حجم در مقایسه با سایر شکلهای انرژی، ناچیز است. هرچند که در مواردی مانند مطالعه تنشهای گرمایی در جامدات یا تحلیل دماسنجهای جیوهای، نمیتوان از این فرض استفاده کرد.
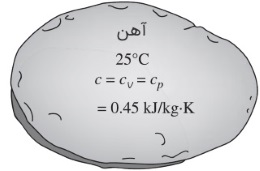
در مادههای تراکم ناپذیر، گرماهای ویژه در حجم و فشار ثابت با هم برابرند. در نتیجه، میتوانیم زیروندهای $$\large c_v$$ و $$\large c_p$$ را برداشته و رابطه زیر را بنویسیم.
$$\large c_p \:=\: c_v \:=\: c$$
تغییر انرژی درونی
همانند گازهای ایدهآل، گرماهای ویژه در مادههای تراکم ناپذیر نیز فقط به دما وابسته است. بنابراین میتوانیم در تعریف $$\large c_v$$ به جای مشتق جزئی از مشتق معمولی استفاده کنیم. از این رو، تغییر انرژی درونی به صورت زیر خواهد بود.
$$\large \text{d}u \:=\: c_v \text{d}T \:=\: c(T) \text{d} T$$
تغییر انرژی درونی بین دو حالت ۱ و ۲ را با محاسبه انتگرال دیفرانسیل انرژی درونی به دست میآوریم.
$$\large \Delta u \:=\: u_2 \:-\: u_1 \:=\: \int_{1}^{2} c(T) \text {d}T\: ~~~ ~~~ (kJ/kg)$$
پیش از اینکه به محاسبه انتگرال بالا اقدام کنیم، تغییرات گرمای ویژه $$\large c$$ با دما باید مشخص باشد. اگر تغییرات دما کوچک باشد، میتوانیم از مقدار $$\large c$$ در دمای متوسط استفاده کنیم. در این حالت، پارامتر $$\large c$$ ثابت بوده و از زیر انتگرال خارج میشود.
$$\large \Delta u\: \cong\: c_{avg} (T_2 \:-\: T_1)\: ~~~ ~~~ (kJ/kg)$$
تغییر آنتالپی
با استفاده از تعریف مفهوم آنتالپی ($$\large h\:=\: u\:+ \:Pv$$) و توجه به این نکته که حجم ثابت است، شکل دیفرانسیلی تغییر آنتالپی در مادههای تراکم ناپذیر به صورت زیر است.
$$\large \text{d}v \:=\:0 \\~\\
\large \text{d}h\:=\: \text{d}u\:+ \:v \text{d}P \:+\: P \text{d}v \:=\: \text{d}u \:+\: v \text{d}P$$
با محاسبه انتگرال رابطه بالا، نتیجه زیر حاصل میشود.
$$\large \Delta h\:=\: \Delta u\:+ \:v \Delta P \:\cong\: c_{avg}\Delta T \:+\: v \Delta P$$
در مورد جامدات، عبارت $$\large v\Delta P$$ ناچیز است و میتوان از تقریب $$\large \Delta h \:=\: \Delta u \:\cong\: c_{avg} \Delta T$$ استفاده کرد. ولی در مورد مایعات، باید به حالتهای زیر توجه کرد.
- فرآیندهای فشار ثابت ($$\large \Delta P \:=\: 0$$)، مانند آنچه در هیترها رخ میدهد: $$\large \Delta h \:\cong\: c_{avg} \Delta T$$
- فرآیندهای دما ثابت ($$\large \Delta T \:=\: 0$$)، مانند فرآیندهایی که در پمپها اتفاق میافتد: $$\large \Delta h \:=\: v\Delta P$$
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز به شما پیشنهاد میشوند:










با سلام
ممنون از اطلاعات خوب و مفید . مهندس ظرفیت گرمایی ویژه نمک مذاب رو چطور محاسبه میکنیم . ۶۰درصد NaNo3 , نیترات پتاسیمKNO3 40درصد .
سلام
ممنون مطلب مفیدی بود
فقط میخواستم بدونم منابع این مقاله چیا هستن؟
و دوم اینکه بخش مربوط به نیروهای بین المولکولی یکم گنگه چطوری میتونم اطلاعات بیشتری ازش بدونم؟
سلام، وقت شما بخیر؛
منبع کلیه مطالب مجله فرادرس در انتهای آنها و پس از بخش معرفی آموزشها و مطالب مرتبط ذکر شدهاند.
در رابطه با نیروهای بین مولکولی نیز میتوانید به این مطلب از مجله فرادرس مراجعه کنید.
از همراهی شما با مجله فرادرس و ارائه بازخورد درباره محتوای آن بسیار سپاسگزاریم.
سلام وقت به خیر ببخشید من یه سوال داشتم الان گرما ویژه آب بالای یه کوه مرتفع بیشتر یا در سطح دریا ؟
سلام؛
با توجه به اينكه ظرفيت گرماي ويژه تابع جرم و دما مي باشد c = f(m,T) ( و برابر است با مقدار گرمائي كه به يك كيلو گرم ماده مورد نظر داده مي شود تا دماي آن يك درجه افزايش يابد ) لذا ظرفيت گرماي ويژه به ارتفاع از سطح دريا مرتبط نيست و در نتيجه ظرفيت گرماي ويژه در سطح دريا و بالاي كوه يكسان است.
احتمالا شما اين بحث را با دماي جوش آب قاطي كردين. كه براي دماي جوش آب: به دليل كاهش فشار هوا با افزايش ارتفاع از سطح دريا، كم مي شود. و در مكاني مثل بالاي يك كوه كه داراي ارتفاع بيشتري نسبت به سطح دريا دارد، دماي جوش آب كمتر است يعني كمتر از 100 درجه سانتي گراد ( كه براي ارتفاع در سطح دريا است ) مي باشد.