گرماسنجی یا کالریمتری — به زبان ساده

انرژی حرارتی را به سادگی نمیتوان اندازهگیری کرد اما تغییر دمای حاصل از جریان انرژی حرارتی بین اشیا یا مواد، قابل اندازهگیری است. گرماسنجی یا کالریمتری شامل مجموعهای از روشهایی است که بمنظور اندازهگیری تغییرات آنتالپی در یک فرآیند شیمیایی انجام میگیرد که این اندازهگیریها به کمک دستگاهی به نام گرماسنج یا کالریمتر انجام میشود.
مقادیر اندازهگیری شده در آزمایش گرماسنجی یعنی تغییر در دمای دستگاه، باید به نوعی با گرمای مصرفی یا تولیدی در واکنش شیمیایی مرتبط شود. ادامه این متن را با توضیح چگونگی جریان انرژی حرارتی و تاثیر آن بر دمای اجسام دنبال میکنیم.
ظرفیت حرارتی
میدانیم زمانیکه جسمی، انرژی گرمایی (حرارتی) میگیرد یا از دست میدهد، دمای آن نیز تغییر پیدا میکند. مقدار این تغییر دما به دو عامل زیر بستگی دارد:
- مقدار انرژی حرارتی منتقل شده (q)
- ظرفیت حرارتی جسم (C): مقدار انرژی مورد نیاز برای افزایش دمای یک جسم به میزان ۱ درجه سانتیگراد. واحد ظرفیت حرارتی، ژول بر درجه سلسیوس است. البته توجه داشته باشید، تغییر ۱ درجه سانتیگراد، دقیقا برابر با تغییر ۱ کلوین خواهد بود. بنابراین، واحد ظرفیت حرارتی را میتوان به صورت ژول بر کلوین هم تعریف کرد.
تغییر دما به صورت زیر بدست میآید:
در این رابطه، q مقدار حرارت (بر اساس ژول)، «C» ظرفیت حرارتی و «»، دمای نهایی منهای دمای اولیه است. با توجه به اینکه تغییرات دما، در کلوین و سانتیگراد، به یک میزان رخ میدهند، بنابراین تفاوتی ندارد که به هنگام محاسبه ، از کدام واحد استفاده میکنیم. تنها چیزی که باید در نظر بگیریم این است که هر دو دمای نهایی و اولیه، واحد یکسانی داشته باشند.
مقدار C به طور ذاتی، عددی مثبت است اما و هر کدام میتوانند مثبت یا منفی باشند. البته علامت آنها باید با یکدیگر یکسان باشند. اگر و مقدار مثبتی داشته باشند، حرارت از محیط به جسم منتقل میشود و اگر این دو عدد، منفی باشند، گرما از جسم به محیط جریان مییابد.
ظرفیت حرارتی یک جسم به جرم و اجزای سازنده آن بستگی دارد. به طور مثال، اگر جرم یک جسم، دو برابر شود، ظرفیت حرارتی آن نیز دو برابر خواهد شد. بنابراین، به هنگام گرماسنجی زمانی که ظرفیت حرارتی یک ماده را گزارش میکنیم باید مقدار ماده نیز در آن لحاظ شود.
ظرفیت حرارتی مولی
ظرفیت حرارتی مولی به مقدار انرژی مورد نیاز برای افزایش دمای یک مول از ماده به مقدار ۱ درجه سانتیگراد میگویند. با توجه به تعریف ارائه شده، واحد به صورت «» ذکر میشود. زیروند «p» بیان میکند اندازهگیری در فشار ثابت انجام شده است.
ظرفیت حرارتی ویژه
«ظرفیت حرارتی ویژه» (Specific Heat Capacity) به مقدار انرژی مورد نیاز برای افزایش دمای ۱ گرم از یک ماده به میزان ۱ درجه سانتیگراد میگویند. بنابراین، واحد ظرفیت حرارتی ویژه به صورت تعریف میشود.
ارتباط مقادیر با مول و جرم
میتوان مقدار ماده، گرمای منتقل شده و ظرفیت حرارتی و تغییرات دمای آنرا به کمک رابطه زیر به یکدیگر مرتبط کرد.
- : تعداد مول ماده
- : ظرفیت حرارتی مولی
همچنین، این مقادیر را میتوان از طریق جرم نیز به یکدیگر مرتبط کرد که در اینصورت، و به ترتیب، گرمای ویژه و جرم خواهند بود.
گرمای ویژه برخی از مواد در جدول زیر آورده شدهاند. توجه داشته باشید که در این جدول، گرمای ویژه بیشتر جامدات، کمتر از است درحالیکه برای بیشتر مایعات این عدد در حدود ذکر میشود. آب در حالتهای جامد و مایع، نوعی استثنا محسوب میشود. ظرفیت حرارتی یخ، بیش از دو برابر ظرفیت حرارتی اکثر جامدات است.
| نام ترکیب - ظرفیت حرارتی ویژه | نام ترکیب - ظرفیت حرارتی ویژه |
| آب (جامد) - 2/108 | آلومینیوم (جامد) - 0/897 |
| آب (مایع) - 4/184 | آهن (جامد) - 0/449 |
| آب (گاز) - 2/062 | مس (جامد) - 0/385 |
| متانول - 2/531 | جیوه (مایع) - 0/140 |
| اتانول - 2/438 | نمک طعام (جامد) - 0/864 |
| نرمال هگزان - 2/270 | منیزیم اکسید (جامد) - 0/921 |
| بنزن - 1/745 | کوارتز - 0/742 |
| گرافیت - 0/709 | کلسیت - 0/915 |
| الماس - 0/509 | طلا - 0/129 |
مقدار بالای گرمای ویژه آب مایع، کاربردهای بسیاری در زندگی روی زمین دارد. جرم مشخصی از آب برای افزایش دمای یک درجهای خود، پنج برابر بیشتر از سنگ آهک یا گرانیت به گرما نیاز دارد. به همین دلیل، در مناطق ساحلی سیاره زمین، تغییرات آب و هوایی کمتری را نسبت به سایر مناطق شاهد هستیم.
در تابستان، بعد از جذب مقادیر زیاد انرژی حرارتی از خورشید، این انرژی به آرامی در زمستان آزاد میشود و به همین دلیل، مناطق ساحی در زمستان، گرمتر از مناطق دیگر هستند.
ظرفیت آب برای جذب مقادیر زیادی از انرژی، بدون افزایش چشمگیر دما را دلیل برای گرم کردن استخرها میتوان دانست زیرا برای حفظ دمای مطلوب، باید به طور مستمر این محیطها را گرم کرد. علاوه بر این، از آنجایی که در حدود ۷۰ درصد بدن انسان را آب تشکیل میدهد، برای افزایش دمای بدن انسان به میزان ۱ درجه سانتیگراد، به مقادیر بسیاری از انرژی نیاز داریم.

مثال محاسبه انرژی ذخیره شده آب
یک واحد ذخیره انرژی خورشیدی از ۴۰۰ لیتر آب برای ذخیره انرژی حرارتی استفاده میکند. در یک روز آفتابی، دمای اولیه آب برابر با ۲۲ درجه سانتیگراد است. در طول روز، دمای آب با چرخش در میان دیوارها، تا ۳۸ درجه سانتیگراد افزایش مییابد. چه میزان انرژی در آب ذخیره شده است. چگالی آب در دمای ۲۲ درجه سانتیگراد برابر با ۰/998 گرم بر لیتر است.
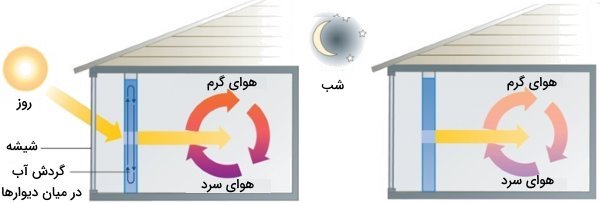
برای حل این سوال در ابتدا از چگالی آب استفاده میکنیم تا جرم معادل با ۴۰۰ لیتر محاسبه شود و در نهایت، با استفاده از روابط بالا و جایگذاری مقادیر مربوطه، گرمای جذب (ذخیره) شده در آب، محاسبه خواهد شد.
بنابراین، به ترتیب برای محاسبه جرم آب و تغییرات دما، خواهیم داشت:
$$\begin{align*} \require {cancel} &= 400 \; \cancel{L}\left ( \dfrac{1000 \; \cancel{mL}}{1 \; \cancel{L}} \right ) \left ( \dfrac{0.998 \; g}{1 \; \cancel{mL}} \right ) \\[4pt] &= 3.99\times 10^{5}g\; {H_2O} \end{align*}$$
تغییرات دما نیز از رابطه زیر محاسبه میشود:
با استفاده از دادههای جدول بالا و روابط داده شده، میزان گرمای ذخیره شده را محاسبه میکنیم:
$$\begin{align*} \require {cancel} q &=mC_{s}\Delta T \\[4pt] &= \left ( 3.99 \times 10^{5} \; \cancel{g} \right )\left ( \dfrac{4.184 \; J}{\cancel{g}\cdot \cancel{^{o}C}} \right ) \left ( 16.0 \; \cancel{^{o}C} \right ) \\[4pt] &= 2.67 \times 10^{7}\,J = 2.67 \times 10^{4}\,kJ \end{align*}$$
زمانی که دو جسم با دمای متفاوت در تماس با یکدیگر قرار بگیرند، گرما از جسم گرم به جسم سرد جریان مییابد. این فرآیند تا زمانی ادامه پیدا میکند که دمای هر دو جسم، یکسان شود. بر اساس قانون پایستگی انرژی، انرژی کل در طول فرآیند تغییر نمیکند.
رابطه بالا بیانگر این است که مقدار گرمای جریانیافته از جسم گرمتر برابر با مقدار گرمای جریانیافته به جسم سردتر خواهد بود. از آنجایی که جهت حرارت برای هر جسم، بر خلاف دیگری است، علامت آنها نیز باید مخالف یکدیگر باشند.
با جایگذاری رابطه بالا در رابطهای که پیشتر بدست آوردیم به رابطه زیر میرسیم:
با بازآرایی رابطه فوق، رابطه زیر را خواهیم داشت:
مثال تعادل حرارتی بین مس و آب
اگر ۳۰ گرم لولهای مسی در دمای ۸۰ درجه سانتیگراد را در ۱۰۰ گرم آب ۲۷ درجه سانتیگراد قرار دهیم، دمای نهایی را محاسبه و فرض کنید هیچ گرمایی به محیط منتقل نمیشود.
برای حل این مساله باید را برحسب دمای نهایی منهای دمای اولیه برای آب و مس بنویسیم و مقادیر مناسب، جایگزین عبارات در رابطه شوند. بنابراین، خواهیم داشت:
با جایگذاری مقادیر داده شده، دمای نهایی را بدست میآوریم.
$$\begin{align*} \left [ \left (30 \; g \right ) \left (0.385 \; J \right ) \left (T_{final} - 80.0 ^oC \right ) \right ] _{Cu} + \left [ (100\,g) (4.18\, J/^oC) \left (T_{final} - 27.0 ^oC \right ) \right ] _{H_{2}O} &=0 \\[4pt] \left[T_{final}\left ( 11.6 \; J/ ^{o}C \right ) -924 \; J \right] + \left[ T_{final}\left ( 418.4 \; J/ ^{o}C \right ) -11,300 \; J \right]&= 0 \\[4pt] T_{final}\left ( 430 \; J/\left ( g\cdot ^{o}C \right ) \right ) &= 12,224 \; J \\[4pt] T_{final} &= 28.4 \; ^{o}C \end{align*}$$
انتظار داشتیم که دمای آب افزایش پیدا کند زیرا لوله مسی، دمای بیشتری نسبت به آب داشت. با این وجود، افزایش دما چشمگیر نیست زیرا جرم آب، به طور تقریبی سه برابر بیشتر از جرم لوله مسی بود. البته، گرمای ویژه آب نسبت به مس، بسیار بیشتر است و این عامل، تاثیر بیشتری هم دارد.
گرماسنجی فشار ثابت
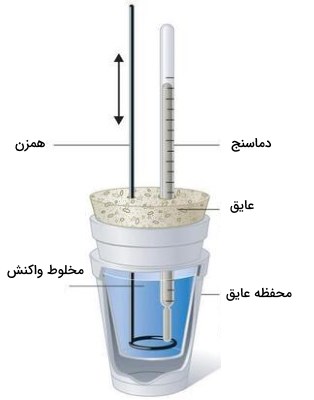
از آنجایی که را به صورت گرمای جریانیافته در فشار ثابت تعریف میکنند، اندازهگیریهای انجام شده در فشار ثابت، به طور مستقیم را بدست میدهد. دستگاه مخصوص این کار به خوبی برای مطالعه واکنشهای شامل محلول در فشار ثابت اتمسفری مورد استفاده قرار میگیرد. شکل ساده آن موسوم به «گرماسنج لیوانی» (Coffee-cup Calorimeter) در تصویر زیر نشان داده شده است. از این دستگاه، بیشتر در آزمایشگاههای شیمی عمومی استفاده میشود.
اساس کار سایر گرماسنجهای تجاری نیز به همین ترتیب است با این تفاوت که در آنها میتوان نمونههای محلول کمتری را استفاده کرد و عایقبندی آنها نیز شکل بهتری دارد. از آنجایی که گرمای آزاد شده یا جذب شده در فشار ثابت، برابر با است، رابطه بین گرما و به صورت زیر تعریف میشود:
مثال گرمای محلول پتاسیم هیدروکسید
هنگامی که ۵/03 گرم پتاسیم هیدروکسید جامد را در ۱۰۰ میلیلیتر آب مقطر در درون یک گرماسنج لیوانی حل کنیم، دمای مایع از ۲۳ درجه به ۳۴/7 درجه سانتیگراد افزایش پیدا میکند. چگالی آب در این بازه دمایی برابر با 0/9969 گرم بر سانتیمتر مکعب است. مقدار تغییر آنتالپی محلول را بر حسب کیلوژول بر مول حساب کنید.
فرض کنید که گرماسنج، مقدار ناچیزی گرما جذب میکند و به دلیل مقدار بالای حجم آب، گرمای ویژه محلول، با گرمای ویژه آب خالص برابر است.
برای حل این سوال به روش زیر عمل میکنیم:
- در ابتدا، جرم محلول را از حجم و چگالی آن بسدت میآوریم و تغییرات دمای محلول را محاسبه میکنیم.
- جریان گرمایی شامل واکنش انحلال را با جایگذاری مقادیر مناسب در رابطه، بدست میاوریم.
- از جرم مولی پتاسیم هیدروکسید برای محاسبه تغییرات آنتالپی استفاده میکنیم.
برای محاسبه در ابتدا باید میزان گرمای آزاد شده در آزمایش گرماسنجی را بدست آوریم. جرم محلول برابر به صورت زیر بدست میآید:
= جرم محلول
تغییرات دما نیز به صورت زیر محاسبه میشود:
$$\Delta T = (34.7\, ^oC − 23.0 \,^oC) = +11.7\, ^oC. $$
از آنجایی که محلول حاصل، غلظت بالایی ندارد (مولاریته آن برابر با 0/9 مولار است)، فرض میکنیم که گرمای ویژه محلول با گرمای ویژه آب برابر باشد. جریان حرارتی به صورت زیر محاسبه میشود:
$$\begin{align*} q_{calorimater}&=mC_{s} \Delta T \\[4pt] &=\left ( 104.72 \; \cancel{g} \right ) \left ( \dfrac{4.184 \; J}{\cancel{g}\cdot \cancel{^{o}C}} \right )\left ( 11.7 \; ^{o}C \right ) \\[4pt] &=5130 \; J = 5.13 \; kJ \end{align*}$$
این آزمایش نشان میدهد که انحلال ۵/03 گرم پتاسیم هیدروکسید در آب، با انرژی 5/13 کیلوژول همراه است. به دلیل افزایش دمای محلول، انحلال پتاسیم هیدروکسید در آب، واکنشی گرماده است.
در آخرین مرحله از محاسبات، به کمک جرم مولی پتاسیم هیدورکسید، را محاسبه میکنیم:
گرماسنجی حجم ثابت
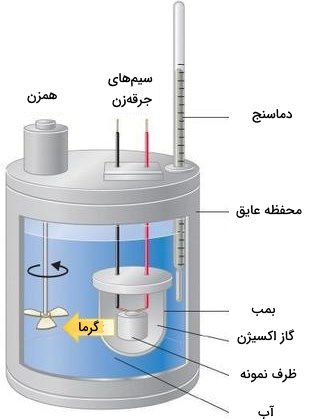
گرماسنجی فشار ثابت برای مطالعه واکنشهای شامل یک یا چند نوع گاز، همچون واکنش سوختن، مناسب نیست. در نتیجه، تغییرات آنتالپی در واکنشهای سوختن به کمک کالریمتر حجم ثابت صورت میگیرد که از جمله آنها میتوان به گرماسنج بمبی اشاره کرد. در تصویر زیر، نمایی از یک گرماسنج بمبی را مشاهده میکنید. واکنشدهنده، درون یک فنجان یا محفظه فولادی با حجم ثابت موسوم به بمب قرار میگیرد. این بمب به همراه اکسیژن اضافی، عایقکاری میشود و درون یک حمام آبی با مقدار مشخصی آب قرار میگیرد.
از آنجایی که واکنشهای سوختن، گرماده هستند، دمای حمام آبی و گرماسنج به هنگام انجام واکنش، افزایش مییابد. اگر ظرفیت حرارتی بمب و جرم آب، مشخص باشند، گرمای آزاد شده را میتوان محاسبه کرد.
با توجه به اینکه حجم سیستم (در داخل بمب) ثابت است، واکنش در شرایط حجم ثابت (و فشار متغیر) انجام میگیرد. گرمای آزاد شده در واکنش، در حجم ثابت، برابر با تغییر انرژی درونی خواهد بود. توسط رابطهای وابسته به تغییر تعداد مولهای گاز در واکنش به مرتبط میشود.
تفاوت بین جریان حرارتی اندازهگیری شده در حجم ثابت و تغییرات آنتالپی، به طور معمول بسیار ناچیز است. با فرض ، رابطه بین تغییر دمای اندازهگیری شده و تغییر آنتالپی واکنش سوختن در رابطه زیر نشان داده شده است که در آن، ، برابر با ظرفیت گرمایی بمب فولادی و حمام آبی اطراف آن است.
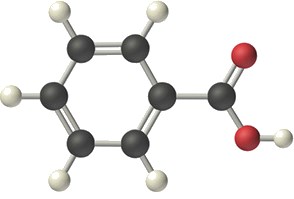
برای اندازهگیری ظرفیت گرمایی کالریمتر، در ابتدا نمونهای را به دقت وزن میکنیم که مقدار آنتالپی سوختن آنرا داشته باشیم. برای این منظور به طور معمول از بنزوییک اسید با فرمول استفاده میکنند چراکه جامدی بلوری است و میتوان آنرا با خلوص بالا بدست آورد.
سوختن بنزوییک اسید در گرماسنج بمبی، به ازای هر گرم، انرژی برابر با 26/38 کیلوژول آزاد میکند . روش گرماسنجی برای اندازهگیری مقدار در مثال زیر بررسی شده است.
مثال محاسبه تغییرات آنتالپی در سوختن گلوکز
سوختن 0/579 گرم از بنزوییک اسید در گرماسنج بمبی سبب افزایش دمای 2/08 درجه سانتیگراد در گرماسنج شده است. در ادامه، گرماسنج تخیله و با اکسیژن اضافی و ۱/732 گرم گلوکز پر میشود. سوختن گلوکز سبب افزایش دما به میزان 3/64 درجه سانتیگراد خواهد شد. را حساب کنید.
در ابتدا، مقدار را برای بنزوییک اسید از طریق ضرب جرم بنزوییک اسید در محاسبه میکنیم. سپس به کمک روابط داده شده، ظرفیت حرارتی کالریمتر از و محاسبه میشود.
در ادامه، باید گرمای آزاد شده به هنگام سوختن گلوکز را محاسبه کنیم که برای این کار، ظرفیت حرارتی بمب در تغییر دما ضرب میشود. به کمک جرم مولی گلوکز و ضرب مقدار گرمای آزاد شده به ازای هر گرم، جرم مولی گلوکز بدست میآید.
حل
به کمک و سایر اطلاعات داده شده، را از جرم بنزوییک اسید بدست میآوریم.
$$\begin {align*} \require {cancel} q_{comb} &= \left ( 0.579 \; \cancel{g} \right )\left ( -26.38 \; kJ/\cancel{g} \right ) \\[4pt] &= - 15.3 \; kJ \end{align*}$$
با توجه به استراتژی بالا برای حل مساله، حال از ظرفیت حرارتی بمب برای محاسبه مقدار گرمای آزاد شده در طول واکنش سوختن گلوکز استفاده میکنیم:
$$\begin{align*} q_{comb} &=-C_{bomb}\Delta T \\[4pt] &= \left ( -7.34 \; kJ/^{o}C \right )\left ( 3.64 \; ^{o}C \right ) \\[4pt] &=- 26.7 \; kJ \end{align*}$$
از آنجایی که سوختن ۱/۷۳۲ گرم گلوکز، ۲۶/۷ کیلوژول انرژی آزاد میکند، به صورت زیر محاسبه میشود.

جمع بندی گرماسنجی
در انتها، موارد زیر را برای جمعبندی مبحث گرماسنجی ارائه میکنیم.
- آنتالپی، نوعی تابع حالت است که بمنظور سنجش گرمای منتقل شده از یک سیستم به محیط یا برعکس در فشار ثابت مورد استفاده قرار میگیرد. لازم به ذکر است که میتوانیم تنها تغییرات آنتالپی را محاسبه کنیم. توجه داشته باشید که مقدار منفی برای یعنی جریان از محیط به سیستم وارد میشود.
- گرماسنجی برای سنجش تغییرات آنتالپی در طول یک فرآیند شیمیایی مورد استفاده قرار میگیرد که در آن، مقدار تغییر دما وابسته به مقدار گرمای آزاد شده یا جذب شده و همچنین وابسته به ظرفیت گرمایی سیستم است. برای گرماسنجی از دستگاهی به نام گرماسنج یا کالریمتر استفاده میکنیم که تغییرات دما در طول یک واکنش شیمیایی را اندازهگیری میکند.
- ظرفیت گرمایی به مقدار انرژی مورد نیاز برای افزایش دما به میزان ۱ درجه سانتیگراد میگویند و واحد آن، ژول بر درجه سلسیوس است. گرمای ویژه یک ماده به مقدار انرژی مورد نیاز برای افزایش دمای ۱ گرم از ماده به میزان ۱ درجه سانتیگراد میگویند. همچنین، ظرفیت گرمایی مولی ، به مقدار انرژی مورد نیاز برای افزایش دمای ۱ مول ماده به ازای ۱ درجه سانتیگراد گفته میشود.
- روشهای گرماسنجی را میتوان در فشار ثابت برای محاسبه مستقیم یا به کمک گرماسنج بمبی در حجم ثابت انجام داد که گرماسنج بمبی به طور ویژه بمنظور اندازهگیری آنتالپی سوختن مورد استفاده قرار میگیرد.












الییییییییییییییییییییییییی