پیوستگی و بقای جرم در سیالات — از صفر تا صد

در مطالب قبلی وبلاگ فرادرس، مفاهیم پایه‌ای مانند استاتیک و سینماتیک سیالات مورد بررسی قرار گرفتند. همانطور که اشاره شد، قوانین بقای جرم (پایستگی جرم) و پیوستگی در اکثر مسائل مرتبط با مکانیک سیالات مورد استفاده قرار می‌گیرند. در این مسائل، برای محاسبه سرعت جریان سیال از معادلات ناویر-استوکس استفاده می‌شود. این معادلات اولین بار در سال 1822 توسط «ناویر» (Claude-Louis Navier) بیان و بعدها توسط «استوکس» (George Gabriel Stokes) در حالات خاصی تکمیل شدند.

معادلات ناویر-استوکس برای تحلیل میدان سرعت جریان سیال مورد استفاده قرار می‌گیرند و برای محاسبه و استفاده از آن‌ها نیاز به آشنایی با مفهوم بقا و پیوستگی در سیالات است. در واقع اکثر مسائل پیچیده در مکانیک سیالات و علم دینامیک سیالات محاسباتی با استفاده از معادلات ناویر-استوکس و پیوستگی قابل حل هستند. بنابراین قدم اول در این مسائل، آشنایی با مفهوم پیوستگی و قانون بقای جرم است. در این مطلب، مفاهیم و شیوه استخراج معادلات پیوستگی و بقای جرم در حالات مختلف مورد بحث قرار می‌گیرند و در انتهای هر بخش با استفاده از مثالی، کاربرد این مفاهیم و روابط نشان داده می‌شود.

بقای جرم - پیوستگی

در مکانیک سیالات، به یک جز کوچک سیال که شامل تعداد بسیار زیادی مولکول است «حجم کنترل» (Control Volume) می‌گویند. تعریف حجم کنترل و مشخص کردن مرزهای آن، یکی از اساسی‌ترین مسائل در علم مکانیک سیالات برای تعیین معادلات بقای جرم و پیوستگی است و این مطلب به بیان دقیق مفاهیم مرتبط با آن می‌پردازد. در ادامه نشان داده می‌شود که حجم کنترل می‌تواند ساکن و یا متحرک باشد و همچنین شکل آن نیز با زمان تغییر کند.

برای تعریف پیوستگی ابتدا کمیت‌های شدتی و مقداری را تعریف می‌کنیم. «کمیت شدتی» (Intensive Property)، خاصیتی از یک ماده است که به اندازه سیستم و یا مقدار آن ماده بستگی نداشته باشد. برای مثال، دما و چگالی یک جسم با نصف کردن آن جسم تغییر نمی‌کنند، بنابراین این دو خاصیت، کمیت‌های شدتی هستند. به خواصی که اندازه آن‌ها به اندازه سیستم و یا مقدار ماده بستگی دارند «کمیت‌های مقداری» (Extensive Property) می‌گویند. برای مثال، جرم، حجم و گرمای منتقل شده از جسم کمیت‌های مقداری هستند.

معادله پیوستگی به صورت کلی، تغییرات یک کمیت شدتی مانند L را در یک سیستم بیان می‌کند. لازم به ذکر است که سیستم به صورت مجموعه‌ای از اجزا تعریف می‌شود که ویژگی‌های اساسی این اجزا در طول زمان بدون تغییر باقی می‌مانند. برای بیان معادله پیوستگی ابتدا به بررسی مفهوم «بقای جرم» (Conservation of Mass) می‌پردازیم. معادله بقای جرم برای یک سیستم که در یک میدان جریان سیال قرار دارد به شکل زیر قابل تعریف است:

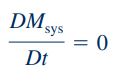
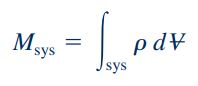
این روابط نشان می‌دهند که جرم سیستم در طول زمان ثابت می‌ماند. همچنین دقت شود که انتگرال نشان داده شده در رابطه بالا، روی حجم سیستم اعمال می‌شود. این معادلات به وضوح بیان می‌کنند که در یک سیستم بسته، جرم سیستم در طول یک فرایند ثابت باقی می‌ماند. در ادامه برای بیان جزئیات روابط بقای جرم و پیوستگی (پایستگی جرم)، از فرم رایج معادله انتقال رینولدز استفاده می‌کنیم. که این معادله به شکل زیر نمایش داده می‌شود:

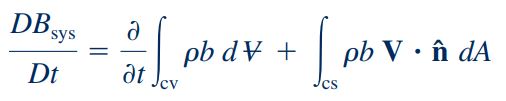
سمت چپ این معادله، نرخ تغییرات کمیت مورد نظر ما در سیستم را بیان می‌کند. ترم اول در سمت راست رابطه بالا، نشان دهنده انتگرال روی حجم کنترل است و شامل ترم‌های «چشمه» (source) و «چاه» (sink) می‌شود. ترم دوم سمت راست معادله انتقال رینولدز نیز نشان دهنده انتگرال‌گیری روی سطح‌های حجم کنترل مورد نظر ما است. این قسمت معادله بیان می‌کند که چه مقدار سیال از مرز‌های حجم کنترل به سمت داخل و یا خارج آن عبور می‌کند.

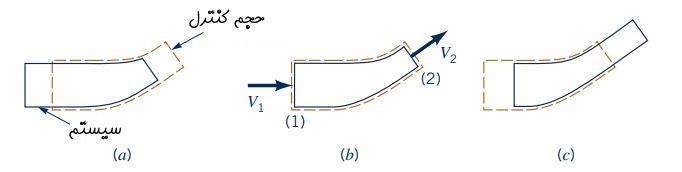
در صورتی که پارامتر مورد نظر در معادله انتقال رینولدز (B) برابر با جرم در نظر گرفته شود، مقدار متغیر  b برابر با یک می‌شود. در نهایت با اعمال معادله انتقال رینولدز روی یک حجم کنترل ثابت و بدون تغییر شکل که در تصویر بالا نشان داده شده است، معادله نهایی به فرم زیر در می‌آید.

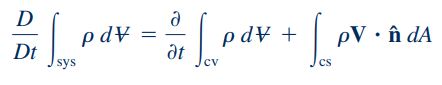
سمت چپ معادله بالا، نرخ زمانی تغییرات جرم سیستم را نشان می‌دهد و به صورت مجموع دو ویژگی مهم از حجم کنترل بیان می‌شود که عبارات سمت راست معادله را تشکیل می‌دهند. عبارت اول، نرخ زمانی تغییرات جرم در داخل حجم کنترل را به شکل زیر نشان می‌دهد.

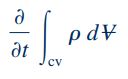
همچنین عبارت دوم، جریان جرمی از طریق مرزهای حجم کنترل را مطابق با معادله زیر نشان می‌دهد.

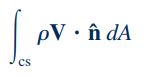
عبارت داخل انتگرال بالا، حاصل ضرب سرعت عمود بر قسمت کوچکی از سطح مقطع ($$V.\hat{n}$$) را در دیفرانسیل سطح مقطع (dA)، نشان می‌دهد. علاوه بر این، همانطور که در شکل زیر نشان داده شده است، در صورتی که مقدار $$V.\hat{n}$$ مثبت باشد، جهت جریان سیال به سمت خارج از مرزهای حجم کنترل است و در صورتی که مقدار $$V.\hat{n}$$ منفی باشد جهت جریان سیال به سمت داخل حجم کنترل است.

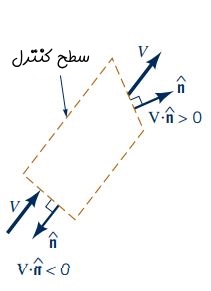
بنابراین انتگرال فوق حاصل جمع عبارت $$\rho V.\hat{n}dA$$، روی تمام سطوح حجم کنترل است و می‌توان آن را به فرم زیر نشان داد.

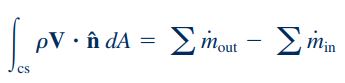
در رابطه بالا، $$\dot{m}$$ جریان جرمی را نشان می‌دهد و می‌توان نتیجه گرفت که اگر عبارت سمت چپ معادله، مقدار مثبتی داشته باشد جریان خالص به سمت خارج از حجم کنترل است و در صورتی که حاصل عبارات سمت چپ معادله، مقداری منفی باشد، جریان خالص به سمت داخل حجم کنترل است.

معادله بقای جرم را می‌توان برای حالت پایا بازنویسی کرد. توجه شود که در حالت پایا، تمامی خواص میدان جریان از جمله چگالی ثابت می‌مانند. بنابراین از ترم اول سمت راست معادله (3) صرف نظر می‌شود. به عبارت دیگر در حالت پایا رابطه زیر برقرار است:

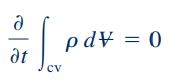
بنابراین برای بیان معادله بقای جرم به فرم حجم کنترلی، معادلات ۱، ۲ و ۳ را با یکدیگر ترکیب می‌کنیم. نتیجه نهایی به فرم رابطه زیر خواهد بود که به آن «معادله پیوستگی» (Continuity Equation) می‌گویند.

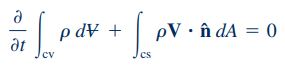
محاسبه سرعت متوسط

معمولا برای محاسبه جریان جرمی از یک سطح مقطع مشخص سیال به مساحت A، از رابطه زیر استفاده می‌شود.

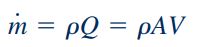
در این رابطه $$\rho$$ چگالی، Q دبی حجمی و V سرعت متوسط جریان سیال عمود بر سطح مقطع A است. از رابطه بالا برای محاسبه سرعت (V) و چگالی ($$\rho$$) متوسط یک سیال نیز استفاده می‌شود. در اکثر مسائلی که ما با آن‌ها سر و کار داریم سیال به صورت غیر قابل تراکم در نظر گرفته می‌شود و چگالی آن تغییر نمی‌کند. بنابراین در چنین مسائلی، چگالی نقطه‌ای و متوسط سیال در یک سطح مقطع، یکسان هستند.

برای محاسبه سرعت متوسط سیال عبوری از سطح مقطع A، جریان جرمی محاسبه شده توسط رابطه بالا را با جریان جرمی حاصل از رابطه انتگرالی برابر می‌گذاریم. رابطه انتگرالی محاسبه جریان جرمی که در بخش قبلی به آن اشاره شد، به فرم زیر است.

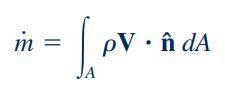
بنابراین سرعت متوسط سیال مطابق با رابطه زیر محاسبه می‌شود.

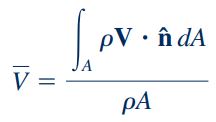
مثال

لوله‌ای به شعاع R را مطابق شکل زیر در نظر بگیرید. سیالی غیر قابل تراکم به صورت پایا در آن جریان دارد. در مقطع «1»، سرعت سیال برابر با مقدار ثابت U است و جهت آن در تمامی نقاط، موازی با محور لوله است. در مقطع «2»، پروفیل سرعت سیال به صورت متقارن و سهموی است به طوری که مقدار آن روی دیواره برابر با صفر و در مرکز لوله ماکزیمم ($$u_{max}$$) است. برای راهنمایی، رابطه‌ سرعت بر حسب فاصله از مرکز لوله برای مقطع «2» در شکل نشان داده شده است. در این مسئله ابتدا رابطه بین سرعت مقطع «۱» (U) و ماکزیمم سرعت مقطع «2» ($$u_{max}$$) را بیابید. سپس به محاسبه رابطه بین سرعت متوسط در مقطع «2» و و $$u_{max}$$ بپردازید.

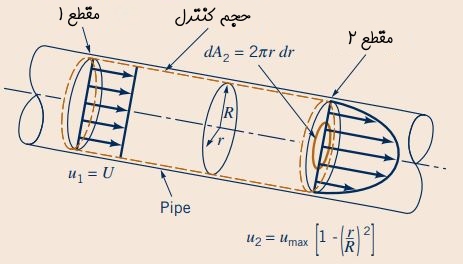
انتخاب مناسب حجم کنترل، اولین گام برای پاسخ به این مسئله است. حجم کنترل مورد نظر در شکل بالا با خط‌چین نمایش داده شده است. در ابتدا رابطه پیوستگی که در بخش قبلی بیان کردیم را برای این حجم کنترل می‌نویسیم. توجه به این نکته ضروری است که ترم اول معادله پیوستگی برای جریان پایا برابر با صفر است. بنابراین داریم:

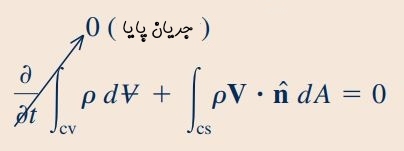
در مقطع «1» سرعت سیال، مقداری ثابت و برابر با U دارد، بنابراین معادله پیوستگی در مقطع «1» به صورت رابطه زیر بیان می‌شود:

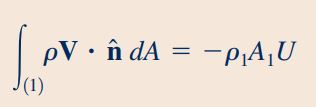
سرعت سیال در مقطع «۲» یکنواخت نیست و برای محاسبه انتگرال موجود در معادله پیوستگی، نیاز به تعیین dA است. بنابراین dA را مطابق با شکل زیر به صورت یک واشر به شعاع r و ضخامت dr در نظر می‌گیریم. این واشر مساحتی برابر با dA دارد.

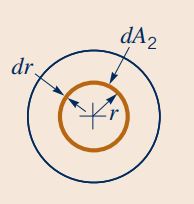
بنابراین دبی جرمی عبوری از مقطع ۲ با استفاده از رابطه زیر قابل محاسبه است.

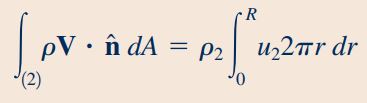
دبی جرمی عبوری از مقطع‌های ۱ و ۲ باهم برابر هستند. بنابراین با ترکیب معادلات ۱، ۲ و ۳ رابطه زیر برای سیال به دست می‌آید.

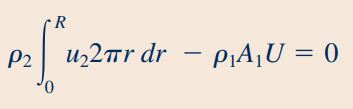
در ادامه با توجه به فرض غیر قابل تراکم بودن سیال، چگالی مقطع‌های «1» و «2» را با یکدیگر برابر قرار می‌دهیم و در نهایت رابطه سرعت مقطع «2» که به صورت سهومی است را در رابطه بالا وارد می‌کنیم.

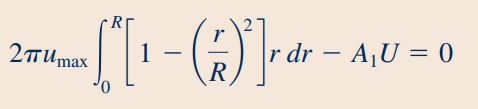
با انتگرال گیری از رابطه بالا در طول شعاع لوله به رابطه زیر می‌رسیم و ارتباط بین سرعت مقطع «۱» (U) و ماکزیمم سرعت مقطع «2» ($$u_{max}$$) به دست می‌آید.

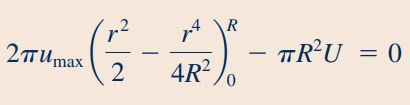
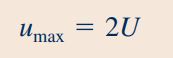
روش عمومی محاسبه سرعت متوسط در سیالات، استفاده از رابطه‌ای است که در درس‌نامه ارائه شد. در اینجا می‌دانیم که سیال مورد نظر در این مسئله غیر قابل تراکم است و در این شرایط، سرعت متوسط سیال در تمامی مقاطع لوله یکسان در نظر گرفته می‌شود. بنابراین رابطه بین سرعت متوسط در مقطع «2» و و $$u_{max}$$ به فرم زیر قابل محاسبه است.

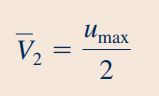
تعمیم معادله پیوستگی برای حجم کنترل متحرک و بدون تغییر شکل

در قسمت‌های قبل، معادله پیوستگی را در حالتی بیان کردیم که حجم کنترل ثابت بود و تغییر شکلی در آن رخ نمی‌داد. در ادامه به بررسی معادله پیوستگی با فرض حجم کنترل متحرک و بدون تغییر شکل می‌پردازیم و روابط حاکم بر آن را مورد بررسی قرار می‌دهیم. همانطور که در قسمت قبلی اشاره شد انتخاب حجم کنترل مناسب، مهمترین گام در پاسخگویی به مسائل مکانیک سیالات است و در صورتی که حجم کنترل به درستی انتخاب نشده باشد، محاسبات لازم چندین برابر خواهند شد. این موضوع در قالب مثال‌، مورد بررسی قرار گرفته است.

در برخی از مسائل انتخاب حجم کنترل متصل به مرجع متحرک، موجب سادگی راه حل مسئله می‌شود. برای مثال یک هواپیمای در حال حرکت را در نظر بگیرید. در صورتی که حجم کنترل، موتور جتی باشد که با هواپیما در حال حرکت است، مسئله به سادگی قابل حل است. مهم‌ترین پارامتر در این مسائل، سرعت سیال نسبت به حجم کنترل متحرک است که برای محاسبه آن می‌توان از رابطه زیر استفاده کرد. در این رابطه، ارتباط بین سرعت‌های مختلف نشان داده شده است.

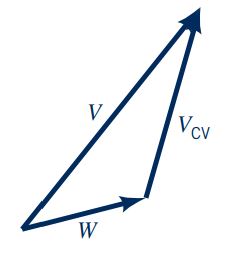
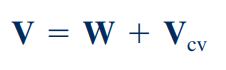
W سرعت نسبی سیال را نشان می‌دهد و برابر با سرعتی است که توسط ناظر متحرک با حجم کنترل، دیده می‌شود. $$V_{cv}$$ سرعت حجم کنترل را نشان می‌دهد که برابر با سرعت حجم کنترل نسبت به ناظر ساکن است. V نیز سرعت مطلق سیال است که نسبت به ناظر ساکن اندازه‌گیری می‌شود.

برای محاسبه معادله پیوستگی، رابطه بین سرعت‌ها که در معادله بالا نشان داده شده است را در معادله انتقال رینولدز وارد می‌کنیم. در نهایت رابطه پیوستگی اصلاح شده، به فرم زیر در می‌آید:

مثال

یک آب‌‌پاش چرخان را مطابق شکل زیر در نظر بگیرید. دبی جرمی این آب‌پاش، ثابت و برابر با 1000ml/s است. مساحت مقطع خروجی آن همانطور که در شکل زیر نیز نشان داده شده، برابر با $$30mm^2$$ است. سرعت متوسط جریان خروجی آب‌پاش در سه حالت مختلف را به‌دست آوردید؛ در حالت اول، آب‌پاش را به صورت ساکن فرض کنید، در حالت دوم سرعت چرخش قسمت بالای آب‌پاش را برابر با 600rpm در نظر بگیرید و در حالت سوم فرض کنید که قسمت بالایی آب‌پاش در ابتدا ساکن است و سپس سرعت چرخش آن تا مقدار 600rpm افزایش می‌یابد.

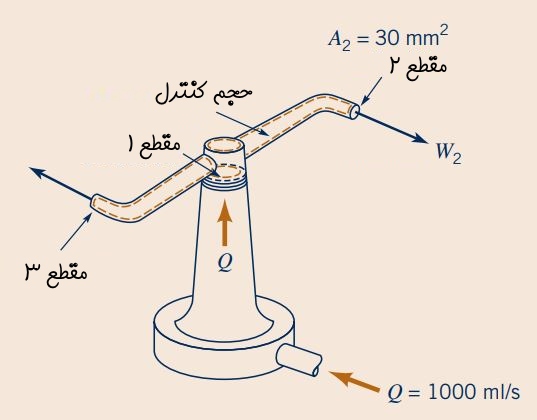
حجم کنترل را برابر با قسمت چرخان آب‌پاش در نظر می‌گیریم. بنابراین حجم کنترل انتخاب شده، تغییر شکل نمی‌دهد و سرعت آن برابر با سرعت قسمت چرخان آب‌پاش است. لذا معادله پیوستگی برای حالت چرخان را به شکل زیر می‌نویسیم.

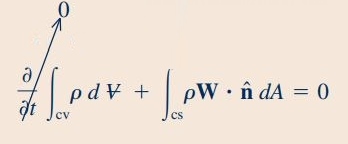
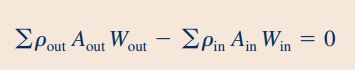
با توجه به پایا بودن جریان و غیرقابل تراکم بودن سیال، ترم اول معادله پیوستگی برابر با صفر است (توجه شود که در هر لحظه، تمام حجم کنترل توسط سیال پوشانده شده است). در رابطه زیر، ورودی سیال که در قسمت پایین آب‌پاش قرار دارد را با نقطه (1) و دو خروجی در بالای آب‌پاش را با نقاط (2) و (3) نمایش می‌دهیم.

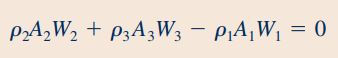
در این مسئله همانطور که در صورت سوال نیز بیان شد، سیال به صورت غیرقابل تراکم فرض شده است و چگالی سیال در نقاط (1)، (2) و (3) با یکدیگر برابر هستند.

رابطه دبی حجمی به صورت $$Q=A_{1}W_{1}$$ و مقدار آن در ورودی آب‌پاش برابر با 1000ml/s داده شده است. با توجه به رابطه دبی حجمی و برابری مساحت سطح دو مقطع (2) و (3)، می‌توان نتیجه گرفت که سرعت خروجی سیال از این دو مقطع یکسان است. این نتیجه را در رابطه بالا قرار می‌دهیم و سرعت متوسط سیال در خروجی آب‌پاش را به شکل زیر محاسبه می‌کنیم.

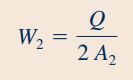
نکته جالبی که در اینجا مشاهده می‌شود این است که مقدار مطلوب مسئله، یعنی سرعت متوسط جریان خروجی آب‌پاش، مستقل از سرعت دوران قسمت فوقانی آب‌پاش است. بنابراین سرعت متوسط سیال در خروجی آب‌پاش در هر سه قسمت سوال، یکسان هستند.

اگر در این مسئله، سرعت خروج سیال از دید ناظر ساکن خواسته شده بود، پاسخ مسئله برای حالات مختلف، متفاوت بود و مقدار آن به اندازه سرعت‌ دورانی قسمت چرخان آب‌پاش، بستگی داشت. نکته دیگر این است که اگر حجم کنترل در این مسئله به شکل مناسبی در نظر گرفته نمی‌شد، پاسخ به آن به این راحتی امکان‌پذیر نبود.

تعمیم معادله پیوستگی برای حالتی که حجم کنترل تغییر شکل دهد

در روابطی که تاکنون به بررسی آن‌ها پرداختیم، حجم کنترل قابلیت تغییر شکل نداشت. در برخی از مسائل، در صورتی که حجم کنترل به صورت تغییر شکل پذیر در نظر گرفته شود، راه حل مسئله بسیار ساده‌تر خواهد بود. بنابراین در ادامه به بررسی این نوع از مسائل و روابط حاکم بر آن‌ها پرداخته می‌شود.

ابتدا معادله انتقال رینولدز را برای این حالت می‌نویسیم.

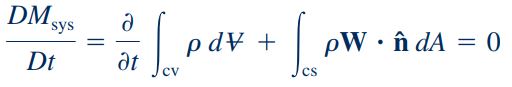
ترم اول در سمت راست این معادله، نشان دهنده نرخ زمانی تغییرات جرم است. در حالتی که حجم کنترل تغییر شکل می‌دهد مقدار این ترم عموما برابر با صفر نیست. ترم دوم در سمت راست معادله بالا برابر با جریان جرمی است و به کمک رابطه سرعت نسبی سیال نسبت به سطح کنترل تعریف می‌شود. این رابطه در حالتی که حجم کنترل تغییر شکل می‌دهد، به شکل زیر است.

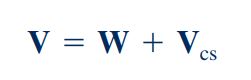
در این رابطه $$V_{cs}$$، سرعت سطح کنترل از دید ناظر ساکن است. دقت کنید که در این قسمت با توجه به تغییر شکل حجم کنترل، سرعت سطح کنترل در تمام مرزهای آن یکسان نیست. برای بررسی دقیق مفهوم حجم کنترلی که قابلیت تغییر شکل دارد، مثال زیر آورده شده است.

مثال

یک سرنگ مطابق شکل زیر برای مصارف دامپزشکی مورد استفاده قرار می‌گیرد. سطح مقطع قسمت مخزن آن برابر با $$500mm^2$$ است و سیال باید با دبی حجمی $$300cm^3/min$$ و به صورت پایا به بدن دام تزریق شود. فرض کنید دبی حجمی نشتی از قسمت انتهایی سرنگ 0.1 مقدار دبی حجمی نوک سرنگ است. در این حالت سرعت دسته‌ی سرنگ را محاسبه کنید.

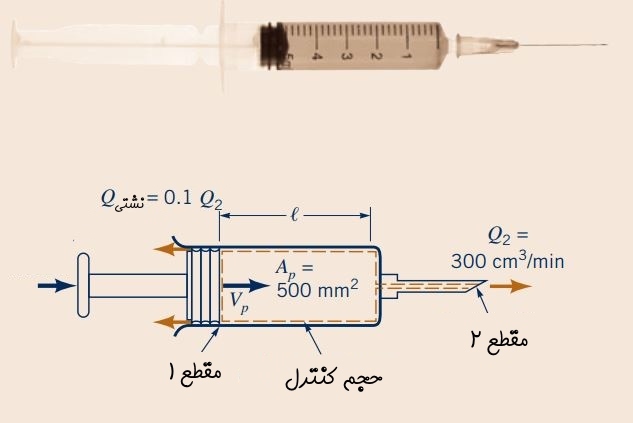
حجم کنترل انتخاب شده در این مثال، با استفاده از خط‌چین در شکل بالا نشان داده شده است. همانطور که در این شکل مشاهده می‌شود، قسمت اول سطح کنترل با حرکت دسته‌ی سرنگ، تغییر شکل می‌دهد. سطح مقطع قسمت ابتدای حجم کنترل (مقطع ۱) برابر با سطح مقطع مخزن سرنگ در نظر گرفته شده است.

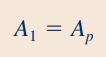
قسمت دوم سطح کنترل (مقطع ۲) که در شکل بالا نشان داده شده، ثابت و سطح آن برابر با $$A_2$$ است. بنابراین معادله انتقال رینولدز را می‌توان به فرم زیر نمایش داد.

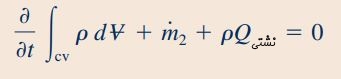
در این مسئله مقدار _نشتیQ و جریانی که از مقطع $$A_2$$ عبور می‌کند پایا هستند ولی نرخ تغییرات زمانی سیال در حجم کنترل به دلیل کوچک شدن حجم کنترل برابر با صفر نیست. با توجه به این توضیحات عبارت زیر را داریم:

در رابطه بالا، $$l$$ برابر با میزان تغییر طول حجم کنترل است. این مورد در شکل ابتدای مثال نیز به تصویر کشیده شده است. نکته دیگر این است که تغییرات حجم نوک سرنگ برابر با صفر است. بنابراین مشتق رابطه بالا به فرم زیر در می‌آید.

برای ساده‌سازی این رابطه باید توجه کرد که میزان نرخ تغییر طول حجم کنترل، برابر با سرعت دسته‌ی سرنگ است که در این مثال به دنبال آن هستیم. بنابراین داریم:

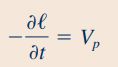
اگر روابط بالا را در معادله انتقال رینولدز جایگذاری کنیم، این معادله به فرم زیر در می‌آید.

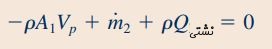
در ادامه برای ساده‌سازی معادله بالا، نیاز به رابطه‌ای بین دبی جرمی در قسمت دوم حجم کنترل و دبی حجمی آن داریم، این رابطه را به فرم زیر نمایش می‌دهیم.

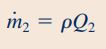
رابطه فوق را در معادله انتقال رینولدز قرار می‌دهیم و با ساده‌سازی روابط، سرعت دسته‌ی سرنگ را بر حسب مقادیر معلوم و موجود در صورت سوال محاسبه می‌کنیم.

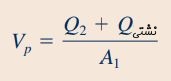
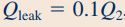
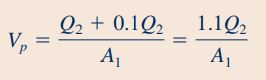
با جایگذاری مقادیر دبی حجمی و مساحت سطح مقطع در رابطه بالا، مقدار نهایی سرعت دسته‌ی سرنگ به شکل زیر قابل محاسبه است.

همانطور که اشاره شد، معادلات پیوستگی و بقای جرم در کنار معادلات ناویر استوکس، کاربرد بسیار زیادی در علم دینامیک سیالات محاسباتی (CFD) و محاسبه پارامترهای مختلف سیال مانند سرعت دارند. این مطلب به صورت جامع به بررسی شیوه به دست آمدن معادلات پیوستگی و بقای جرم پرداخته و سپس این معادلات را برای حالات مختلف تعمیم داده و در نهایت و در تمام حالات، برای فهم دقیق مطلب مثالی نیز آورده شده است. در مطالب دیگر وبلاگ فرادرس به بررسی دقیق معادلات مومنتوم خطی، مومنتوم زاویه‌ای و ناویر-استوکس پرداخته شده است.

در صورتی که به مباحث ارائه شده، علاقه‌مند هستید و قصد یادگیری در زمینه‌های مطرح شده در مکانیک سیالات را دارید، آموز‌ش‌های زیر به شما پیشنهاد می‌شود:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های دروس مهندسی شیمی
• مجموعه آموزش‌های نرم‌افزارهای مهندسی مکانیک
• سینماتیک سیالات — مقدمه‌ای بر مکانیک
• استاتیک سیالات — به زبان ساده
• معادلات ناویر استوکس (Navier Stokes) — از صفر تا صد
• دینامیک سیالات محاسباتی (CFD) — از صفر تا صد
• مومنتوم خطی (Linear Momentum) در سیالات — از صفر تا صد