گرمای نهان چیست؟ – به زبان ساده

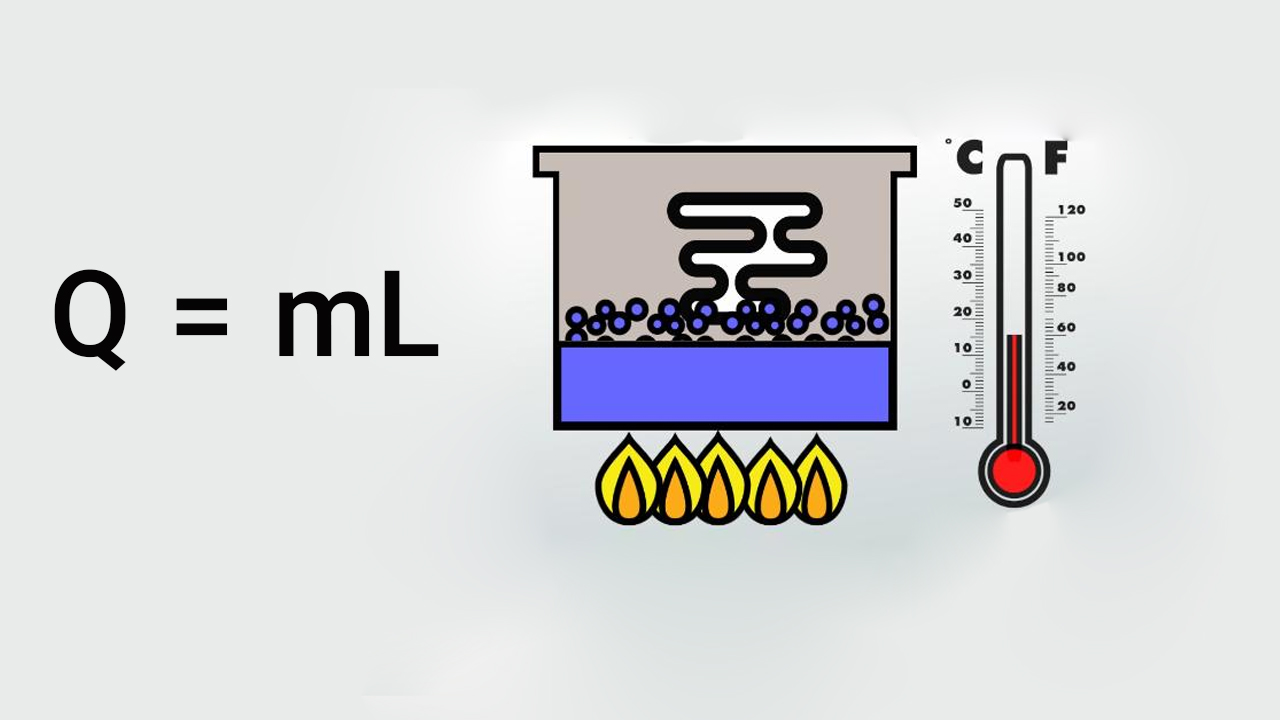
در این روزهای گرم، وقتی از بیرون به خانه بازمی‌گردید، نوشیدن لیوانی آب یخ بسیار لذت بخش خواهد بود. در بیشتر مواقع، برای خنک کردن آب از تکه‌های یخ استفاده می‌کنید. پس از انداختن یخ در لیوان و پس از مدت زمان مشخصی، یخ‌ها ذوب می‌شوند و دمای آب کاهش خواهد یافت. در اینجا با مفاهیمی به نام‌های گرمای نهان و محسوس برخورد می‌کنیم. به مقدار گرما یا انرژی جذب یا رها شده به هنگام تغییر فاز ماده، بدون تغییر دما، گرمای نهان گفته می‌شود. در این مطلب، در مورد گرمای نهان، انواع،  فرمول‌های محاسبه و تفاوت آن با گرمای محسوس به زبان ساده صحبت می‌کنیم.

گرمای نهان چیست ؟

به مقدار انرژی آزاد شده یا جذب شده به هنگام تغییر حالت در دمای ثابت، گرمای نهان می‌گوییم. به زبان علمی‌تر، فاز ماده در دمای ثابت با جذب یا آزاد سازی انرژی، تغییر می‌کند. فاز ماده، شکلی از ماده با ویژگی‌های فیزیکی و شیمیایی یکنواخت در سراسر آن است. به تغییر فاز ماده، انتقال فاز گفته می‌شود. یکنواختی فیزیکی و شیمیایی در فاز جدید نیز باید مشاهده شود. ماده برای تغییر فاز، انرژی را به شکل گرما جذب یا آزاد می‌کند. به این انرژی مبادله شده، گرمای نهان گفته می‌شود.

سه فاز اصلی ماده عبارت هستند از:

• جامد
• مایع
• گاز

مقدار گرمای نهان با طبیعت ماده تغییر می‌کند. انواع گرمای نهان عبارت هستند از:

• گرمای نهان ذوب: به مقدار گرمای لازم بر حسب ژول برای تبدیل جامد به مایع در نقطه ذوب و در دمای ثابت، گرمای نهان ذوب گفته می‌شود.
• گرمای نهان تبخیر: به مقدار گرمای لازم برای تبدیل مایع به گاز در نقطه جوش و در دمای ثابت، گرمای نهان تبخیر می‌گوییم.
• گرمای نهان انجماد: به هنگام انجماد آب (یخ زدن آب) در نقطه انجماد و دمای ثابت، مقداری انرژی آزاد می‌شود. به این انرژی، گرمای نهان انجماد گفته می‌شود.
• گرمای نهان تصعید: تصعید فرایند فیزیکی است که طی آن ماده جامد مستقیم و بدون تبدیل به حالت مایع، به گاز تبدیل می‌شود. به مقدار انرژی لازم برای تبدیل واحد جرم از حالت جامد به گاز در دمای ثابت، گرمای نهان تصعید می‌گوییم.

در تعریف گرمای نهان گفتیم که تغییر فاز در دمای ثابت رخ می‌دهد، اما سوالی که ممکن است برای شما مطرح شود آن است که چگونه تبادل انرژی در دمای ثابت رخ می‌دهد. برای پاسخ به این پرسش باید با مفهومی به نام انرژی درونی آشنا باشیم. انرژی داخلی ماده جامد برابر مجموع انرژی‌های جنبشی و پتانسیل است. انرژی جنبشی همان حرکت انتقالی است. انرژی متوسط ذرات داخل ماده با دمای ماده مرتبط است. انرژی پتانسیل ناشی از پیوند اتم‌ها با یکدیگر است.

با افزایش انرژی جنبشی ذرات در مایع، دو اتفاق رخ می‌دهد:

• ذرات با سرعت بیشتری حرکت می‌کنند.
• دمای مایع افزایش می‌یابد.

در این حالت، پیوند بین مولکولی ذرات را کنار یکدیگر نگه داشته است. بنابراین، انرژی داخلی ذرات تنها انرژی جنبشی یا پتانسیل ذرات تشکیل‌دهنده ماده نیست، بلکه مجموع انرژی جنبشی و انرژی پتانسیل آن‌ها است. با تغییر فاز ماده از حالت مایع به جامد، مقدار انرژی جنبشی داخلی قابل توجه خواهد شد.

برای درک بهتر این موضوع، مثال ساده‌ای را مطرح می‌کنیم. غروب یک روز گرم تابستان به خانه بازمی‌گردید و برای رفع تشنگی و اندکی خنک شدن، مقداری یخ با دمایی در حدود ۵- درجه سلسیوس را در لیوان آبی با دمای حدود ۲۰ درجه می‌اندازید. پس از گذشت مدت زمان مشخصی، آب خنک را می‌نوشید. دمای آب و یخ را با استفاده از دماسنج اندازه می‌گیرید و عدد صفر درجه سلسیوس را مشاهده می‌کنید. دمای ترکیب آب و یخ در صفر ثابت می‌ماند، در واقع:

•  دمای یخ از ۵- درجه سانتی‌گراد به صفر درجه سلسیوس افزایش می‌یابد.
• دمای آب از ۲۰ درجه سلسیوس به صفر درجه سلسیوس کاهش می‌یابد.
• آب و یخ به تعادل گرمایی می‌رسند و دما تغییر نمی‌کند.

ترکیب آب و یخ در دمای صفر، ثابت باقی می‌ماند، اما انرژی به طور پیوسته وارد لیوان می‌شود و یخ با دریافت انرژی، ذوب و به مایع تبدیل می‌شود. سوالی که ممکن است برای شما مطرح شود آن است که چرا دما علی‌رغم دریافت انرژی و تغییر حالت یخ از جامد به مایع، ثابت باقی می‌ماند. برای درک بهتر این موضوع به نمودار زیر دقت کنید. با توجه به نمودار، دمای یخ از ۵- درجه سلسیوس تا صفر درجه سلسیوس افزایش می‌یابد. سپس، با ثابت ماندن دما در صفر، یخ به طور کامل به مایع تبدیل می‌شود. در پایان، با ذوب شدن کامل یخ، دما کم‌کم شروع به افزایش خواهد کرد.

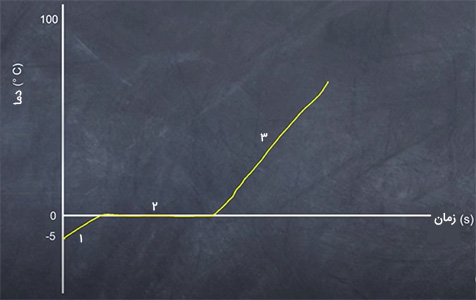
نمودار نشان داده شده در تصویر، به سه مرحله تقسیم شده است:

1. در این مرحله دما متغیر است. با انتقال گرما به سیستم، انرژی جنبشی متوسط ذرات و در نتیجه دما افزایش می‌یابد. در اینجا تغییر حالت یا تغییر فاز رخ نمی‌دهد.
2. در مرحله ۲، دما ثابت می‌ماند، اما تغییر حالت از جامد به مایع رخ می‌دهد. در این حالت، انرژی جذب شده به سیستم صرف شکستن پیوندهای مولکولی (پیوند بین مولکول‌های هیدروژن و اکسیژن در آب) می‌شود.
3. در این مرحله نیز مشابه مرحله یک، تغییر حالت یا تغییر فاز رخ نمی‌دهد. مقدار انرژی جنبشی متوسط و دما نیز افزایش یافته است.

در ادامه، در مورد هر یک از انواع گرمای نهان صحبت خواهیم کرد، اما قبل از آن، گرمای محسوس را تعریف و تفاوت آن با گرمای نهان را توضیح می‌دهیم.

گرمای محسوس چیست ؟

گرمای نهان را به صورت انرژی آزاد یا جذب شده به هنگام تغییر فاز ماده در دمای ثابت تعریف کردیم. در مقابل، گرمای محسوس به صورت انرژی لازم برای تغییر دمای ماده، بدون تغییر فاز، تعریف می‌شود. به بیان دیگر، گرمای محسوس به طور کامل حس می‌شود. به عنوان مثال، خنک‌کننده‌ها با استفاده از گرمای محسوس، کار می‌کنند یا آب جوش گرم‌تر از آب سرد است.

فرق گرمای نهان و گرمای محسوس چیست ؟

تفاوت‌های گرمای نهان و گرمای محسوس در جدول زیر بیان شده است.

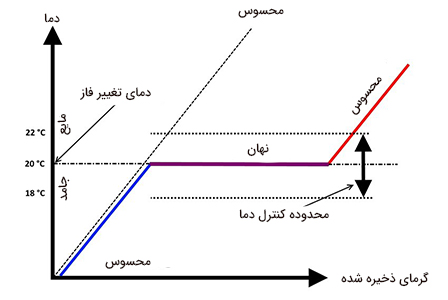
برای درک بهتر تفاوت این دو نوع گرما یا انرژی به تصویر زیر دقت کنید. همان‌طور که در تصویر مشاهده می‌کنید، تغییر دما و فاز ثابت از مشخصه‌های اصلی گرمای محسوس و در مقابل، دمای ثابت و تغییر فاز از ویژگی‌های مشخص گرمای نهان هستند.

مثال های گرمای نهان و گرمای محسوس

زندگی روزمره سرشار از مثال‌هایی از گرمای نهان و گرمای محسوس است:

• به طور حتم بارها برای درست کردن چای یا قهوه، آب را در سماور یا کتری به جوش آورده‌اید. در ابتدا دمای آب در حدود ۲۰ درجه سلسیوس است. ابتدا گرما به کتری و سپس به آب منتقل می‌شود. در این مرحله دمای آب از ۲۰ به ۱۰۰ درجه سلسیوس افزایش می‌یابد. از آنجا که تغییر دمای آب محسوس و هیچ تغییر فازی رخ نداده است، در این مرحله گرمای محسوس، مشاهده می‌شود. به هنگام جوشیدن آب، مقدار زیادی انرژی آزاد می‌شود.

• به طور مشابه، مقدار قابل توجهی انرژی برای تبدیل آب به یخ باید جذب شود. یخچال فریزر با حذف انرژی گرمایی، به آب اجازه تغییر فاز از حالت مایع به جامد (یخ)‌ را می‌دهد. توجه به این نکته مهم است که مقدار گرمای نهان انجماد آب، زیاد است.
• گرمای نهان سبب شدت یافتن طوفان‌ها می‌شود. دمای هوا به هنگام عبور از آب‌های گرم، افزایش می‌یابد و بخار آب را جذب می‌کند. گرمای نهان با متراکم شدن بخار و تشکیل ابرها، در جو رها و گرما در هوا آزاد می‌شود. این گرمای آزاد شده منجر به ایجاد ناپایداری، بالا رفتن ابرها و تشدید طوفان می‌شود.
• گرمای محسوس پس از جذب انرژی خورشید توسط خاک و گرم‌تر شدن آن، آزاد می‌شود.
• خنک شدن از طریق تعریق متأثر از گرمای نهان و محسوس است.

تاکنون، با تعریف گرمای نهان و انواع آن، گرمای محسوس و تفاوت آن با گرمای نهان با ذکر مثال آشنا شدیم. در ادامه، در مورد فرمول گرمای نهان و انواع آن با ذکر مثال آشنا خواهیم شد.

فرمول گرمای نهان چیست ؟

گرمای نهان را به صورت مقدار انرژی لازم برای تغییر ماده از حالتی به حالت دیگر، تعریف کردیم. مقدار آن با استفاده از فرمول زیر به‌دست می‌آید:

$$Q = m L$$

در این رابطه:

• $$Q$$ برابر مقدار انرژی گرمایی آزاد شده یا جذب شده است و بر حسب ژول یا کالری اندازه گرفته می‌شود.
• $$m$$ جرم است و بر حسب کیلوگرم اندازه گرفته می‌شود.
•  $$L$$ گرمای نهان تبخیر، تصعید، ذوب یا انجماد است.

از رابطه بالا هنگامی استفاده می‌کنیم که دما ثابت باشد و تنها تغییر حالت یا فاز داشته باشیم.

در مطالب بالا در مورد گرمای محسوس نیز صحبت کردیم. دانستن فرمول این گرما نیز خالی از لطف نیست:

$$Q = m c \triangle T$$

از رابطه بالا به هنگام تغییر دما و ثابت ماندن فاز، استفاده می‌شود. در این رابطه:

• $$m$$ برابر جرم بر حسب کیلوگرم است.
• $$Q$$ انرژی بر حسب ژول یا کالری است.
• $$\triangle T$$ برابر تغییرات دما بر حسب سلسیوس یا کلوین است.
• $$c$$ ظرفیت گرمایی ویژه نامیده می‌شود. به عنوان مثال، ظرفیت گرمایی ویژه آب برابر $$4180 \ \frac {J} {Kg \ ^oC}$$ است. در واقع، برای افزایش دمای یک کیلوگرم آب به اندازه یک درجه سلسیوس، باید به آن انرژی برابر ۴۱۸۶ ژول بدهیم. بنابراین، ماده‌ای با ظرفیت گرمایی زیاد می‌تواند مقدار زیادی انرژی گرمایی را بدون تغییر زیاد دما، در خود ذخیره کند. مقدار این کمیت در فلزات بسیار کم است. از این رو با دادن اندکی انرژی گرمایی به فلزات، دمای آن‌ها بسیار زیاد خواهد شد. در نتیجه، فلزات رسانای خوب گرما هستند.

مثال محاسبه گرمای نهان

قطعه فلزی با دمای ۲۰ درجه سلسیوس و جرم ۶۰ گرم را در نظر بگیرید. این فلز در جریانی از بخار با دمای ۱۰۰ درجه سلسیوس غوطه‌ور می‌شود و ۰/۵ گرم بخار بر روی فلز می‌نشیند و به مایع تبدیل می‌شود. اگر گرمای نهان تبخیر برابر $$540 \ \frac{cal}{g}$$ باشد، ظرفیت گرمایی فلز را به‌دست آورید.

پاسخ: ظرفیت گرمایی فلز با c نشان داده می‌شود. فلز با دمای ۲۰ درجه سلسیوس در بخاری با دمای بالاتر، یعنی ۱۰۰ درجه سلسیوس قرار می‌گیرد. در نتیجه، اختلاف دمای بین فلز و بخار سبب تغییر دمای فلز خواهد شد. در واقع، دمای فلز از ۲۰ درجه سلسیوس به ۱۰۰ درجه سلسیوس، افزایش می‌یابد. بنابراین، گرمای جذب شده توسط فلز برابر است با:

$$Q = m c \triangle T \\ Q = 60 \times c \times (100 - 20) \\ Q = 60 \times c \times 80 \cal$$

به این نکته توجه داشته باشد که در محاسبه گرمای منتقل شده به فلز، جرم آن به کیلوگرم تبدیل نشده، زیرا واحد ظرفیت گرمایی ویژه کالری بر گرم است.

چون فلز دمای کمتری نسبت به بخار دارد، انرژی گرمایی را از بخار جذب می‌کند. در نتیجه، بخار انرژی گرمایی از دست می‌دهد. از آنجایی که دمای بخار ثابت است و حالت آن از گاز به مایع تغییر کرده است (پس از نشستن بر روی فلز سردتر، به مایع تبدیل می‌شود)، مقدار انرژی گرمایی جذب شده توسط بخار به صورت زیر محاسبه می‌شود:

$$Q = m \times L \\ Q = 0.5 \times (540 \ \frac{cal}{g})$$

انرژی گرمایی جذب شده برابر انرژی گرمایی آزاد شده است:

$$Q_{in} = Q_ {out} \\ 0.5 \times 540 = 60 \times c \times 80 \\ c = 0.056 \ \frac{cal}{g \ ^oC}$$

مثال محاسبه گرمای محسوس

مقدار انرژی لازم برای افزایش دمای ۰/۱۵ کیلوگرم آب از دمای ۲۰ درجه سلسیوس به ۵۵ درجه سلسیوس، چه مقدار است؟

پاسخ: در این مثال، تنها افزایش دما رخ داده و فاز، ثابت است. بنابراین، از فرمول گرمای محسوس استفاده می‌کنیم:

$$Q = m c \triangle T \\ = \frac{0.15 \ kg}{1}\times \frac{4186 \ J }{kg \ ^o C}\times \frac{(55 \ ^o C - 20 \ ^o C)}{1}\\ Q = 21976.5 \ J = 22 \ KJ$$

فرمول گرمای نهان تبخیر چیست ؟

گرمای نهان تبخیر برابر مقدار انرژی لازم برای تبدیل ماده از حالت مایع به گاز در دمای ثابت است و از حاصل‌ضرب جرم جسم در گرمای نهان تبخیر به‌دست می‌آید:

$$Q = m L_V$$

در رابطه فوق:

• $$Q$$ برابر مقدار انرژی جذب شده برای تبدیل ماده از جامد به مایع (مانند تبدیل یخ به آب) است و بر حسب ژول یا کالری اندازه گرفته می‌شود.
• $$m$$ جرم است و بر حسب کیلوگرم اندازه گرفته می‌شود.
•  $$L$$ گرمای ویژه نهان ذوب است.

توجه به این نکته مهم است که اگر تغییر فاز گاز به مایع انجام شود، ماده گرما از دست خواهد داد و مقدار گرمای از دست داده برابر است با:

$$Q = - \ m L_V$$

مثال اول گرمای نهان تبخیر

برای تبدیل تکه سرب مایعی به جرم ۱۰ گرم در دمای ۱۷۵۰ درجه سلسیوس به گاز سرب در دمای ۱۷۵۹ درجه سلسیوس، ۸۵۸۰ ژول انرژی نیاز است. کدام یک از گزینه‌‌ها، گرمای نهان تبخیر سرب، کدام یک از گزینه‌های زیر است؟

1. $$858 \ \frac{kJ}{kg}$$
2. $$296 \ \frac{kJ}{kg}$$
3. $$4726 \ \frac{kJ}{kg}$$
4. $$879 \ \frac{kJ}{kg}$$

پاسخ: در این مثال، تبدیل حالت از مایع به گاز در دمای ثابت رخ داده است. بنابراین، از رابطه گرمای نهان تبخیر استفاده می‌کنیم:

$$Q =+ m L_v$$

علامت مثبت در رابطه فوق نشان‌دهنده جذب گرما توسط سیستم است. با قرار دادن مقدارهای داده شده در رابطه فوق،‌ $$L_v$$ را به‌دست می‌آوریم:

$$Q= + \ m L_v \\ 8580 \ J = (0.010 \ kg) L_v \\ \Rightarrow L_v = 858 \ \frac{kJ}{kg}$$

پاسخ صحیح، گزینه ۱ است.

مثال دوم گرمای نهان تبخیر

مقدار گرمای لازم برای تبدیل ۳۰ گرم یخ در دمای ۵- درجه سلسیوس به بخار در دمای ۱۱۰ درجه سلسیوس کدام یک از گزینه‌های داده شده است؟

($$c_{ice} = 2.090 \ \frac{kJ}{kg. ^o C}, \ c_{water}= 4.18 \ \frac{kJ}{kg. ^o C}, \ c_{steam} = 2.010 \ \frac{kJ}{kg. ^o C}, \ L_f = 333.5 \ \frac{kJ}{kg}, \ L_v = 2260 \ \frac{kJ}{kg}$$)

1. ۹۱ کیلوژول
2. ۱۰۲ کیلوژول
3. ۸۴ کیلوژول
4. ۱۲۵ کیلوژول

پاسخ: مرحله‌های تبدیل یخِ ۵- درجه سلسیوس به بخارِ ۱۱۰ درجه سلسیوس در تصویر زیر نشان داده شده است:

مقدار گرمای محاسبه شده برابر است با:

$$Q_1 = m c_{ice} (0 - (-5)) \\ = 0.030) (2.090) (5) \\ = 0.3135 \ k J \\ Q_2 = mL_f \\ = (0.030)(333.5) \\ = 10.005 \ kJ \\ Q_3 = mc_{water} (100 -0) \\ = (0.030) (4.18) (100) \\ = 12.54 \ kJ \\ Q_4 = mL_v \\ = (0.03) (2260) \\ = 67.8 \ kJ$$

به هنگام تغییر فاز از مایع به بخار از گرمای نهان تبخیر استفاده می‌شود. در پایان، با افزودن گرمای بیشتر به سیستم در حالت بخار، دمای آن افزایش خواهد یافت:

$$Q_5 = m c_{steam} \triangle T \\ = (0.030) (2.010) (110 -100) \\ = 0.603 \ kJ$$

در فرایند بالا، دو تغییر فاز از حالت جامد به مایع (یخ به آب) و مایع به بخار (آب به بخار آب) اتفاق افتاده است. مقدار انرژی کل جذب شده توسط یخ برابر جمع ۵ انرژی محاسبه شده در بالا و برابر است با:

$$Q_{tot} = 91.2 \ kJ$$

بنابراین، پاسخ صحیح گزینه یک است.

مثال سوم گرمای نهان تبخیر

مقدار گرمای آزاد شده توسط ۲۰۰ گرم بخار در ۱۷۵ درجه سلسیوس و تبدیل آن به ۲۰۰ گرم آب در دمای صفر درجه سلسیوس برابر است با:

1. ۲۸۳ کیلوژول
2. ۳۲۶ کیلوژول
3. ۴۸۳ کیلوژول
4. ۵۲۵ کیلوژول

پاسخ: در این مثال، در اثر چگالش، بخار آب به آب تبدیل می‌شود. مسیر این فرایند در تصویر زیر نشان داده شده است:

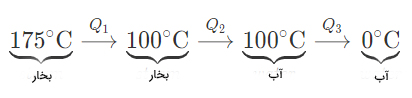
در مرحله اول، تغییر دما رخ داده و دمای بخار آب کاهش یافته است، بنابراین مقدار گرمای آزاد شده در این مرحله برابر است با:

$$Q_1 = m_s c_S \triangle T \\ = (0.200) (2010) (100 -175) \\ = - \ 30150 \ J \\ = -\ 30.15\ k J$$

در مرحله دوم، بخار، سرد و به آب تبدیل شده است. در این مرحله، تغییر فاز در دمای ثابت اتفاق افتاده است. بنابراین، مقدار گرمای آزاد شده برابر است با:

$$Q_2 = - \ m L_V \\ = - \ (0.200\ kg) (2260 \ \frac{kJ}{kg}) \\ =- \ 452 \ kJ$$

به این نکته توجه داشته باشید که علامت منفی نشان‌دهنده گرمای آزاد شده است.

در مرحله سوم، آب سرد و دمای آن کاهش می‌یابد:

$$Q_3 = m_sc_w \triangle T \\ = (0.200 \ kg) (4.186 \ \frac{kJ}{kg. ^ o C}\ (0-100) \\ = - \ 0.8372 \ kJ$$

گرمای آزاد شده توسط سیستم برای تبدیل بخار به آب برابر جمع گرماهای محاسبه شده در بالا و برابر است با:

$$Q_{tot} = 483 \ kJ$$

پاسخ صحیح گزینه ۳ است.

مثال چهارم گرمای نهان تبخیر

۲۰ گرم آلومینیوم در دمای ۲۰۰ درجه سلسیوس و ۳۵ گرم سرب، داخل محفظه‌ای به حجم ۴۵ سانتی‌متر مکعب و حاوی اتیل الکل در دمای ۱۵ درجه سلسیوس قرار داده می‌شوند. پس از گذشت مدت زمان مشخصی، مخلوط به حالت تعادل با دمای ۲۵ درجه سلسیوس می‌رسد. دمای اولیه سرب کدام است؟

(‌$$\rho _{ethyl} = 790 \ \frac{kg}{m^3}, \ c_{ethyl} = 2400 \ \frac{J}{kg . ^o C}, \ c_{Al} = 900 \ \frac{J}{kg . ^o C}, \ c_{Pb} = 128 \ \frac{J}{kg . ^o C}$$)

1. ۲۳۰- درجه سلسیوس
2. ۴۸۷- درجه سلسیوس
3. ۴۸۷+ درجه سلسیوس
4. ۲۳۰+ درجه سلسیوس

پاسخ: در ابتدا، با استفاده از رابطه زیر، جرم اتیل الکل را به‌دست می‌آوریم:

$$m= \rho V \\ = (790 \ \frac{kg}{m^3}) (45 \times 10^{-6} \ m^3) \\ = 0.035550 \ kg \\ = 35.55 \ g$$

در تمام مثال‌های گرمای نهان، یک ماده گرما از دست می‌دهد و ماده دیگر این گرما را جذب می‌کند (فرض می‌کنیم که هیچ تبادل گرمایی با محیط اطراف وجود ندارد). در این فرایندها، بر طبق قانون پایستگی انرژی، مقدار گرمای از دست داده شده باید برابر مقدار گرمای جذب شده باشد.

$$Q_{gained} = m_{ethyl}c_{ethyl} (T_f - T_i) \\ = (0.03555) (2400) (25 - 15) \\ = 853. 2 \ J$$

آلومینیوم برای کاهش دما، گرما آزاد می‌کند:

$$Q_{lost-Al} = m_{Al}c_{Al} (T_f - T_i) \\ = (0.020) (900) (25 - 200) \\ = - \ 3150 \ J$$

دمای اولیه سرب مجهول است، بنابراین فرض می‌کنیم که مقدار آن بالاتر از دمای نهایی مخلوط است. در نتیجه، مقدار انرژی آزاد شده توسط سرب برابر است با:

$$Q_{lost-Pb} = m_{Pb}c_{Pb} (T_f - T_i) \\ = (0.035) (128) (25 - T_i) \\ = 4.48 (25- T_i)$$

بر طبق اصل پایستگی انرژی، مقدار گرمای آزاد شده برابر مقدار گرمای جذب شده است:

$$-(-\ 3150 + 4.48(25 - T_i)) = 853.2 \\ 4.48 (25 - T_i) = 4003.2 \\ \Rightarrow T_i = - \ 487 \ ^oC$$

همان‌طور که دیده می‌شود، دمای اولیه سرب بسیار کمتر از دمای تعادل است و این با فرض اولیه در تناقض است.

اکنون فرض کنید که دمای اولیه سرب پایین‌تر از دمای تعادل است. بر طبق این فرضیه، سرب گرما جذب کرده است. در نتیجه، داریم:

گرمای آزاد شده = گرمای جذب شده

$$-(-\ 3150 ) = 853.2 + 4.48 ( 25 - T_i) \\ \Rightarrow T_i = -487 \ ^oC$$

دمای به‌دست آمده با فرض اولیه سازگار است، بنابراین پاسخ صحیح گزینه ۲ است.

مثال پنجم گرمای نهان تبخیر

۲۰۰ گرم آب در دمای اولیه ۲۷ درجه سلسیوس در محفظه شیشه‌ ۱۰۰ گرمی قرار دارد. چه مقدار بخار در دمای ۱۵۰ درجه سلسیوس، دمای محفظه آب داخل آن را تا ۴۵ درجه سلسیوس افزایش می‌دهد؟

($$c_w = 4186 \ \frac{J}{kg . ^o C}, \ c_g = 837 \ \frac{J}{kg . ^o C}, \ L_v = 2260 \ \frac{kJ}{kg}$$)

1. ۵/۵گرم
2. ۳/۸ گرم
3. ۴/۵ گرم
4. ۶/۵ گرم

پاسخ: در ابتدا، مقدار گرمای لازم برای افزایش دمای محفظه و آب از ۲۷ به ۴۵ درجه سلسیوس را حساب می‌کنیم:

$$Q_{gain} = (m_gc_g + m_wc_w)\triangle T\\ = ( 0.100 \times 837 + 0.200 \times 4186) (45 - 27) \\ = 16576.2 \ J$$

در رابطه بالا، اندیس‌های w و g به ترتیب برای آب و شیشه نوشته شده است. بنابراین، ترکیب محفظه شیشه‌ای و آب برای افزایش دما، ۱۶/۶۷۵ کیلوژول انرژی گرمایی جذب خواهد کرد.

مقدار گرمای آزاد شده توسط بخار برای رسیدن به دمای ۴۵ درجه سلسیوس از مرحله‌های زیر تشکیل شده است:

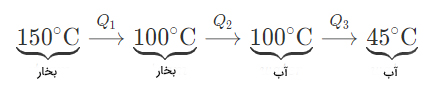
در مرحله سوم، بخار تغییر فاز می‌دهد و به آب تبدیل می‌شود. مقدار گرمای $$Q_1$$ برابر است با:

$$Q_1 = m_sc_s \triangle T \\ = m_s (2.09) (100- 150) \\ \\ = - \ 104.5 \ m_S \ kJ$$

گرمای $$Q_2$$ ناشی از تغییر فاز است و با استفاده از گرمای نهان محاسبه می‌شود:

$$Q_2 = - \ m_s L_V \\ = - \ m_s(2260) \ kJ$$

گرمای $$Q_3$$ ناشی از تغییر دما است و به صورت زیر به‌دست می‌آید:

$$Q_3 = m_sc_w \triangle T \\ = m_s (4.186) (45-100) \\ \\ = - \ 230.23 \ m_S \ kJ$$

مقدار گرمای آزاد شده توسط بخار، برابر جمع گرماهای محاسبه شده در بالا است:

$$Q_{lost} = - \ 2594.73 \ m_s\ kJ$$

بر طبق قانون پایستگی انرژی، گرمای آزاد شده برابر گرمای جذب شده است:

$$2594.73 \ m_S = 16.576 \\ \Rightarrow m_s = 0.0063 \ kg$$

بنابراین، پاسخ صحیح گزینه ۴ است.

فرمول گرمای نهان ذوب چیست ؟

گرمای نهان ذوب برابر مقدار انرژی لازم برای تبدیل ماده از حالت جامد به مایع در دمای ثابت است و با استفاده از فرمول زیر به‌دست می‌آید:

$$Q = m L_F$$

در رابطه فوق:

• $$Q$$ برابر مقدار انرژی جذب شده برای تبدیل ماده از مایع به گاز (مانند تبدیل آب به بخار آب) است و بر حسب ژول یا کالری اندازه گرفته می‌شود.
• $$m$$ جرم است و بر حسب کیلوگرم اندازه گرفته می‌شود.
•  $$L_V$$ گرمای ویژه نهان تبخیر است.

توجه به این نکته مهم است که اگر تغییر فاز مایع به جامد انجام شود، ماده گرما از دست خواهد داد و مقدار گرمای از دست داده برابر است با:

$$Q = - \ m L_F$$

مثال اول محاسبه گرمای نهان ذوب

مقدار انرژی لازم برای ذوب ۴۵۰ گرم یخ را به‌دست آورید.

پاسخ: برای حل این گونه مثال‌‌ها، ابتدا باید به دو سوال زیر پاسخ دهید:

1. آیا تغییر فاز رخ داده است؟
2. آیا دما تغییر کره است؟

در این مثال، یخ در دمای ثابت از حالت جامد به مایع تبدیل می‌شود. در نتیجه، برای محاسبه انرژی لازم برای این تغییر فاز در دمای ثابت از فرمول گرمای نهان ذوب استفاده می‌کنیم:

$$Q = m L_F$$

ذکر این نکته مهم است که در تبدیل جامد به مایع، انرژی باید به سیستم اضافه شود، بنابراین مقدار انرژی مثبت خواهد بود. برای محاسبه انرژی، ابتدا جرم را به کیلوگرم تبدیل می‌کنیم:

$$\frac{450 \ g}{1}\times \frac{1 \ kg}{1000 \ g}= 0.45 \ kg$$

مقدار انرژی اضافه شده به سیستم برابر است با:

$$Q = \frac{0.45 \ kg}{1} \times \frac{3.33 \times 10^6 \ J}{kg} =149890 \ J = 149.85 \ KJ$$

مثال دوم محاسبه گرمای نهان ذوب

مقدار انرژی لازم برای تبدیل ۳ کیلوگرم یخ در دمای صفر درجه سلسیوس به آب در دمای ۳۰ درجه سلسیوس، چه مقدار است؟

پاسخ: در این مثال، تغییر دما و تغییر فاز هر دو اتفاق افتاده است. بنابراین، دو نوع گرمای نهان ذوب و محسوس باید محاسبه شوند.

1. در مرحله نخست تمام یخ در دمای صفر درجه سلسیوس به آب تبدیل می‌شود. در این مرحله دما ثابت ولی تغییر فاز از حالت جامد به مایع رخ داده است. بنابراین، گرمای نهان ذوب باید محاسبه شود.
2. در مرحله دوم، دمای آب از صفر درجه سلسیوس به ۳۰ درجه سلسیوس افزایش یافته است. در این مرحله، تنها دما، بدون تغییر فاز، افزایش می‌یابد. بنابراین، گرمای محسوس باید محاسبه شود.

گرمای مرحله نخست برابر است با:

$$Q = m L_F = (3) (3.33 \times 10^5) = 999000 \ J$$

گرمای مرحله دوم برابر است با:

$$Q = m c \triangle T = (3) (4186) ( +30) = 3376740 \ J$$

مقدار انرژی کل برای تبدیل ۳ کیلوگرم یخ از دمای صفر درجه سلسیوس به آب در دمای ۳۰ درجه سلسیوس برابر جمع انرژی گرمایی دو مرحله است:

$$Q_T = Q_F + Q_{sensible} = 999000 \ J + 376740 \ J =1375740 \ J$$

مثال سوم محاسبه گرمای نهان ذوب

مقدار انرژی اضافه شده به یک گرم طلا برای تغیر فاز آن از جامد به مایع را به‌‌دست آورید. گرمای نهان ویژه طلا برابر $$65.5 \times 10^3 \ \frac{J} {kg}$$ است.

پاسخ: جرم طلا و $$L_F$$ داده شده‌اند. با استفاده از فرمول $$Q = m L_F$$ مقدار گرمای اضافه شده به یک گرم طلا برای تبدیل آن به مایع را محاسبه می‌کنیم:

$$Q = mL_F = (1 \times 10^{-3}) \times (64.5 \times 10^3 \ \frac{J}{kg}) \\ Q = 64.5 \ J$$

مثال چهارم گرمای نهان ذوب

چه مقدار گرما برای تبدیل 2 کیلوگرم یخ در دمای 20- درجه سلسیوس به آب در دمای 100 درجه سلسیوس، لازم است؟ (گرمای ویژه یخ و آب به ترتیب برابر با $$2.09 \ \frac{kJ}{kg . ^0 C}$$ و $$4.18 \ \frac{kJ}{kg . ^0 C}$$ است.)

پاسخ: این پرسش یکی از آسان‌ترین مثال‌های گرمای نهان است. مقدار گرمای کل برای تبدیل یخ به بخار از چهار مرحله تشکیل شده است:

• $$Q_1$$: مقدار گرمای لازم برای تغییر دما از ۲۰- درجه سلسیوس به صفر درجه سلسیوس.
• $$Q_2$$: مقدار گرمای لازم برای ذوب یخ و تغییر فاز.
• $$Q_3$$: مقدار گرمای لازم برای افزایش دما از صفر درجه سلسیوس به 100 درجه سلسیوس.
• $$Q_4$$: مقدار گرمای لازم برای تبخیر آب.

هر یک از این گرماها در ادامه به صورت زیر محاسبه شده‌اند:

در قسمت یک، دما تغییر کرده است، بنابراین داریم:

$$Q_1 = mc_{ice} (T_1 - T_2) \\ = (2) (2.09) (0 - (-20)) = 83.6 \ kJ\\$$

در مرحله بعدی، تغییر فاز از حالت جامد به مایع رخ داده است:

$$Q_2 = mL_f \\ = (2) (333.5)\\ = 667 \ kJ$$

در پایان، دما از صفر به ۱۰۰ درجه سلسیوس افزایش یافته، اما تغییر فاز رخ نداده است:

$$Q_3 = mc_{water} \triangle T \\ = (2) (4.18) (100-0) \\ = 836 \ kJ$$

با جمع کردن گرمای فوق، گرمای کل به‌دست می‌آید:

$$Q = Q_1 + Q_2 + Q_3 = 1586.6 \ kJ$$

مثال پنجم گرمای نهان ذوب

به ۴۰ لیتر آب در دمای ۴۰ درجه سلسیوس در محفظه‌ای عایق، ۴ کیلوگرم یخ در دمای ۱۰- درجه سلسیوس اضافه می‌کنیم. دمای تعادل را به‌دست آورید.

پاسخ: در اینجا دو ماده داریم:

1. یخ: گرما به‌دست می‌آورد و ذوب می‌شود.
2. آب: به دلیل دمای بالاتر، گرما آزاد می‌کند و سردتر می‌شود.

سوالی که ممکن است برای شما مطرح شود آن است که آیا گرمای آزاد شده توسط آب، تمام یخ را آب می‌کند یا خیر. برای پاسخ به این سوال باید مقدار گرمای آزاد شده و جذب شده را محاسبه کنیم:

$$Q_1$$ مقدار گرمای لازم برای افزایش دمای یخ ۱۰- به صفر درجه سلسیوس است:

$$Q_3 = mc_{ice} \triangle T \\ = (4) (4.18) (0-(-10)) \\ = 82 \ kJ$$

$$Q_2$$ مقدار گرمای لازم برای ذوب ۴ کیلوگرم یخ است:

$$Q_2 = mL_f \\ = (4) (333.5) \\ = 1334 \ kJ$$

در نتیجه، گرمای کسب شده توسط یخ برابر است با:

$$Q_{gained} = Q_1 + Q_2 = 1416 \ kJ$$

در ادامه، باید مقدار گرمای آزاد شده توسط آب را به‌دست آوریم. در این مثال، حجم آب داده شده است، بنابراین برای محاسبه گرمای آزاد شده باید جرم آب را به‌دست آوریم:

$$m = \rho V \\ = (1000 \ \frac{kg}{m^3}) (40 \ L) (\frac{1 \ m^3}{1000 \ L}) \\ = 40 \ kg$$

مقدار گرمای آزاد شده توسط آب برابر است با:

$$Q_3 = m c_{water} \triangle T \\ =(\rho V) c \triangle T\\ = (40) (4018) (0 - 40) \\ = -6688 \ kJ$$

علامت منفی نشان‌دهنده آزاد شدن گرما است. با مقایسه بین گرماهای محاسبه شده به این نتیجه می‌رسیم که مقدار گرمای آزاد شده توسط آب برای ذوب تمام یخ و رسیدن آب به دمای نهایی $$T_f$$ کافی است. بنابراین، داریم:

$$Q_{net} = 6688-1416 = 5272 \ kJ \\ Q_{net} = mc_w \triangle T \\ 5272 = (40) (4.18) (T_f - 0) \\ \Rightarrow T_f = 31.53 \ ^oC$$

راه حل دیگر حل این مثال، استفاده از پایستگی انرژی است. به مثال بعد دقت کنید.

مثال ششم گرمای نهان ذوب

قطعه کوچکی یخ در دمای صفر درجه سلسیوس را در یک کیلوگرم آب در دمای اولیه ۱۰ درجه سلسیوس می‌اندازیم. دمای مخلوط را به‌دست آورید. (فرض کنید گرما در محیط اطراف آزاد می‌شود.)

پاسخ: برای حل این مثال از دو روش استفاده می‌کنیم:

روش اول: گرمای جذب شده توسط یخ برای تبدیل آن از یخ صفر درجه به آب صفر درجه برابر است با:

$$Q_{gained} = m_{ice} L_f \\ = (0.200 \ kg) (333.5 \ \frac{kJ}{kg}) \\ = 66.7 \ kJ$$

مقدار گرمای آزاد شده توسط یک کیلوگرم آب برای کاهش دمای آن از ۱۰ به صفر درجه سلسیوس برابر است با:

$$Q_{lost} = m_w c \triangle T \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = (1) (4.18) (0-10) \\ \ \ \ \ \ \ \ \ \ = -41.8 \ kJ$$

با توجه به گرماهای محاسبه شده، یخ به گرمای بیشتری برای ذوب نیاز دارد:

$$Q_{gained} > ∣Q_{lost}∣$$

بنابراین، یخ به طور کامل ذوب نخواهد شد و مقداری یخ در آب باقی می‌ماند.

روش دوم: در این روش از پایستگی انرژی استفاده می‌کنیم:

در ابتدا، فرض می‌کنیم که تمام یخ در دمای صفر درجه سلسیوس ذوب می‌شود. در این مرحله، یخ گرمای آزاد شده توسط آب را جذب می‌کند. از آنجایی که هیچ تبادل گرمایی با محیط اطراف وجود ندارد، جمع گرمای هر مرحله بر طبق قانون پایستگی انرژی برابر صفر خواهد بود:

$$Q_{gained} +Q_{lost} = 0 \\ m_{ice} L_f + m_{ice} c_{ice} (T_f - 0) + m_wc_w (T_f -10) = 0 \\ (0.200) (333.5) + (0.200) (2.09) (T_f - 0 ) + (1) (4.18) (T_f - 10) = 0 \\ \Rightarrow T_f = -5.5 \ ^o C$$

دمای کمتر از صفر درجه سلسیوس صحیح نیست، زیرا کاهش دمای یخ به کمتر از صفر درجه سلسیوس امکان‌پذیر نیست. بنابراین، در پایان، مخلوطی از آب و یخ در دمای تعادل صفر درجه سلسیوس خواهیم داشت.

مثال هفتم گرمای نهان ذوب

قطعه یخ ۸۰ گرمی در دمای صفر درجه سلسیوس را در ۷۲۵ گرم آب در دمای اولیه ۲۴ درجه سلسیوس می‌اندازیم. دمای نهایی مخلوط را به‌دست آورید. ($$c_{water} = 4.18 \ \frac{kJ}{kg . ^o C}$$ و $$c_{ice} = 2.090 \ \frac{kJ}{kg . ^o C}$$ و $$L_f = 333.5 \ \frac {kJ} {kg}$$)

پاسخ: دما آب بالاتر است، بنابراین گرما را آزاد می‌کند:

$$Q_{released} = Q_1$$

یخ، گرمای آزاد شده را جذب می‌کند:

$$Q_{abs} - Q_2 + Q_3$$

در ابتدا، فرض می‌کنیم که تمام یخ ذوب و به ۸۰ گرم آب در دمای $$T_f$$ تبدیل می‌شود. با استفاده از قانون پایستگی انرژی، جمع جبری گرماها باید برابر صفر باشد. در نتیجه، داریم:

$$Q_{released}+ Q_{gained} = 0 \\ m_wc_w (T_f - 24) + m_{ice} L_f + m_{ice} c_{ice} (T_f -0) = 0 \\ (0.725)(4.180)(T_f - 24) + (0.00) (333.5) + (0.080) (4.18) (T_f - 0) = 0 \\ -(3.0305) (T_f - 24) + 26.68 = 0 \\ \Rightarrow T_f = 16.3 \ ^o C$$

بنابراین، دمای تعادل برابر ۱۳/۶ درجه سلسیوس است.

مثال هشتم گرمای نهان ذوب

محفظه‌ای آلومینیومی به جرم ۴۰۰ گرم و گرمای ویژه $$0.900 \ \frac {kJ}{kg . ^ o C}$$ در نظر بگیرید. این محفظه توسط ۵ کیلوگرم اتیل الکل در دمای ۳۰ درجه سلسیوس پر و سپس ۲۰۰ گرم یخ در دمای ۱۵- درجه سلسیوس داخل آن انداخته می‌شود. فرض کنید سیستم از محیط اطراف جدا شده است. دمای تعادل مخلوط را به‌دست آورید.

پاسخ: از آنجایی که محفظه عایق است، هیچ تبادل گرمایی با محیط اطراف وجود نخواهد داشت. بر طبق قانون پایستگی انرژی، جمع گرمای آزاد شده و جذب شده برابر صفر است.

دمای محفظه آلومینیومی و الکل بالاتر است، بنابراین گرما از دست می‌دهند. یخ گرمای آزاد شده را جذب می‌کند. مانند مثال‌های قبل، فرض می‌کنیم که تمام یخ ذوب و به دمای $$T_f$$ بزرگ‌تر از صفر می‌رسد.

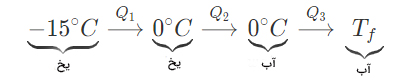
مقدار گرمای کسب شده توسط یخ برابر است با:

$$Q_1 = m_{ice} c_{ice} (0 - (-15)) \\ = (0.200) (2.090) (15) \\ = 6.27 \ kJ \\ \\ Q_2 = m_{ice}L_f \\ = (0.200) (333.5) \\ = 66.7 \ kJ \\ Q_3 = m_{ice} c_{water} (T_f - 0) \\ = (0.200) (4.18) (T_f)$$

بنابراین، انرژی گرمایی کل جذب شده برابر است با:

$$Q_{gained} = Q_1 + Q_2 + Q_3\\ = 72.97 + 0.836 \ T_f$$

در قسمت دیگر، محفظه و الکل گرما را آزاد می‌کنند و به دمای نهایی $$T_f$$، پایین‌تر از دمای اولیه می‌رسند:

$$Q_{lost} = Q_{Al} + Q_{ethyl} \\ = m_{Al} c_{Al} (T_f - 25) + m_{ethyl}c_{ethyl} (T_f - 30) \\ = (0.400)(0.9)( T_f - 25) + (5) (2.4) (T_f - 30) \\ = 12.36 \ T_f - 369$$

بر طبق قانون پایستگی انرژی، تمام گرمای آزاد شده باید توسط یخ جذب شود:

$$Q_{lost} + Q_{gained} = 0 \\ \Rightarrow Q_{gained} = - Q_{lost} \\ 72.97 + 0.836 T_f = - (12.36 T_f - 369) \\ \Rightarrow T_f = 22.43 \ ^o C$$

مثال نهم گرمای نهان ذوب

۲ کیلوگرم آب در دمای ۲۵ درجه سلسیوس را در یخچال فریزر قرار می‌دهیم. چه مقدار گرما توسط فریزر از آب برای تبدیل آن به یخ در دمای ۱۵- درجه سلسیوس، گرفته می‌شود؟ ($$c_{water} = 4.18 \ \frac{kJ}{kg . ^o C} \ , \ c_{ice} = 2.090 \ \frac{kJ}{kg . ^o C}$$)

پاسخ: فرایند انجام شده به صورت زیر است:

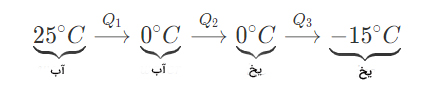
برای محاسبه گرما از رابطه‌های زیر استفاده می‌کنیم:

$$Q = mc \triangle T \\ Q = mL_F$$

گرمای هر مرحله برابر است با:

$$Q_1 = mc_w (0 - 25) \\ = (2) (4.18) (-25) \\ = -209 \ kJ \\ Q_2 = -mL_f \\ = -(2) (333.5) \\ = -667 \ kJ \\ Q_3 = m c_{ice} (-15 -0) \\ = (2) (2.090) (-15) = -62.7 \ kJ$$

با جمع سه گرمای محاسبه شده در بالا، مقدار گرمای کلی گرفته شده از آب برای تبدیل آن به یخ را به‌دست می‌آوریم:

$$Q_{tot} = Q_1 + Q_2 + Q_3 \\ = -209 - 667 -62.7 \\ = -938.7 \ kJ$$

به این نکته توجه داشته باشید که مرحله ۲، فرایند انجماد است و در آن باید از تعریف گرمای نهان انجماد استفاده کنیم. در تمام مثال‌های مربوط به گرما، علامت منفی نشان‌دهنده خروج گرما از سیستم است.

مثال دهم گرمای نهان ذوب

تکه یخی در دمای ۱۵- درجه سلسیوس را از یخچال فریزر خارج می‌کنیم و آن را در محفظه آلومینیومی ۲۰۰ گرمی حاوی ۴۵۰ گرم آب در دمای ۲۴ درجه سانتی‌گراد قرار می‌دهیم. بعد از گذشت مدت زمان مشخصی، تمام یخ آب می‌شود و آب در دمای ۵ درجه سلسیوس در محفظه باقی می‌ماند جرم یخ را به‌دست آورید.

پاسخ: در ابتدا، مشخص می‌کنیم که کدام ماده گرما را جذب می‌کند و کدام گرما از دست می‌‌دهد. از آنجایی که دمای محفظه و آب داخل آن بالاتر از دمای یخ است، گرما از دست می‌دهند و یخ این گرما را جذب می‌کند. فرایند رسیدن از دمای ۱۵- درجه سلسیوس به ۵ درجه سلسیوس به صورت خلاصه در تصویر زیر نشان داده شده است:

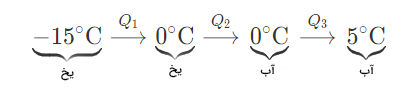
با استفاده از گرمای ویژه و گرمای نهان ذوب، گرمای هر یک از مرحله‌های نشان داده شده در تصویر را محاسبه می‌کنیم:

$$Q_1 = m_{ice} c_{ice} (0 - (-15)) \\ = m_{ice} (2.090) (15) \\ = 31.35 m_{ice} \\ Q_2 = m_{ice} L_f \\ = m_{ice} (333.5) \\ Q_3 = m_{ice} c_{water} (5 -0) = \\ = m_{ice} (4.180))5) \\ = 20.9 m_{ice}$$

گرمای جذب شده توسط یخ برابر با جمع گرماهای محاسبه شده فوق است:

$$Q_{abs} = 385.75 m_{ice}$$

گفتیم محفظه و آب داخل آن گرما را آزاد می‌کنند و از دمای ۲۴ درجه سلسیوس به دمای نهایی ۵ درجه سلسیوس می‌رسند. مقدار گرمای آزاد شده برابر است با:

$$Q_{lost} = (m_{cont} c_{Al} + m_{water} c-{water} ) (5-24) \\ = (0.2 \times 0.9 + 0.450 \times 4.18) (-19) \\ = - \ 39.159 \ kJ$$

علامت منفی به معنای خروج گرما از سیستم است. با برابر قرار دادن گرمای آزاد شده با گرمای جذب شده (قانون پایستگی انرژی)، جرم یخ را به‌دست می‌آوریم:

گرمای جذب شده = گرمای آزاد شده

$$385.75 m_{ice} = - (- 39.159) \\ \Rightarrow m_{ice} = 0.101 \ kg$$

فرمول گرمای نهان تصعید چیست ؟

گرمای نهان تصعید برابر مقدار انرژی لازم برای تبدیل ماده از حالت جامد به گاز در دمای ثابت است و با استفاده از فرمول زیر به‌دست می‌آید:

$$Q = m L_S$$

در رابطه فوق:

• $$Q$$ برابر مقدار انرژی جذب شده برای تبدیل ماده از جامد به گاز (مانند یخ خشک) است و بر حسب ژول یا کالری اندازه گرفته می‌شود.
• $$m$$ جرم است و بر حسب کیلوگرم اندازه گرفته می‌شود.
•  $$L_S$$ گرمای ویژه نهان تصعید است. توجه به این نکته مهم است که گرمای منتقل شده بر واحد جرم، گرمای ویژه نام دارد.

نمودار گرما بر حسب دما

قطعه یخی با جرم دلخواه در دمای ۲۰- درجه سلسیوس در نظر بگیرید. مراحل تبدیل یخ به بخار آب در نمودار دما بر حسب گرما در تصویر زیر نشان داده شده است.

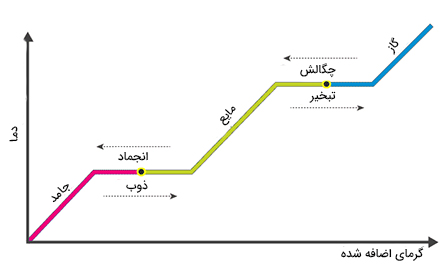
فرض کنید نقطه شروع نمودار دمای ۲۰- درجه سلسیوس است.

• با دادن گرما به یخ دمای آن افزایش می‌یابد.
• در نقطه مشخصی دما ثابت می‌ماند. در این مرحله، با افزودن گرما به سیستم، دما ثابت می‌ماند.
• با دادن گرمای بیشتر به سیستم، دما با شیب متفاوتی شروع به افزایش خواهد کرد.
• در ادامه، دما برای مدت زمان زیادی ثابت باقی می‌ماند.
• با دادن گرمای بیشتر به سیستم، دما در نقطه مشخصی با شیب تندتری شروع به افزایش می‌یابد.

نکته زیر را همواره به یاد داشته باشید:

هرگاه دما ثابت باشد، تغییر فاز رخ می‌دهد.

یخ در دمای صفر درجه سلسیوس شروع به ذوب شدن می‌کند. بنابراین، هنگامی که دما به صفر درجه سلسیوس می‌رسد، ثابت می‌ماند و یخ شروع به ذوب شدن می‌کند. تا تبدیل شدن تمام یخ به آب، دما ثابت باقی خواهد ماند. در این مرحله، با گرفتن گرما از سیستم، آب به یخ تبدیل (انجماد) می‌شود. پس از تبدیل تمام یخ به آب و اضافه شدن گرما به سیستم، دما افزایش خواهد یافت. آب در مای ۱۰۰ درجه سلسیوس به جوش می‌آید. بنابراین، در این دما، با اضافه شدن گرما به سیستم، تمام آب تبخیر و به بخار تبدیل خواهد شد.

مثال نمودار گرما بر حسب دما

مقدار انرژی لازم برای تبدیل ۷/۵ کیلوگرم یخ از دمای ۳۰- درجه سلسیوس به بخار در دمای ۲۰۰ درجه سلسیوس چه مقدار است؟

پاسخ: برای حل این مثال، ابتدا نمودار دما بر حسب گرما را رسم می‌کنیم.

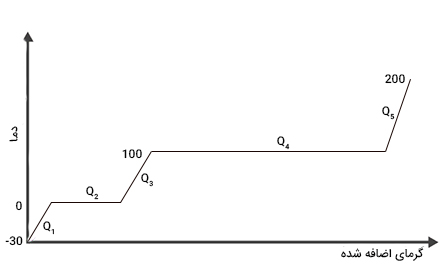
در ادامه، هر یک گرماهای داده شده را به دست می‌آوریم.

• محاسبه $$Q_1$$: در این حالت، دما تغییر کرده است اما فاز ثابت مانده است. بنابراین، از فرمول گرمای محسوس استفاده می‌کنیم:

$$Q_1 = m c \triangle T = 7.5 (2100) (+30 \ ^o C) = 472500 \ J$$

• محاسبه $$Q_2$$: در این حالت، دما ثابت است اما فاز تغییر کرده است (جامد به مایع). بنابراین، از فرمول گرمای نهان ذوب استفاده می‌کنیم:

$$Q_2 = m L_F = 7.5 (3.33 \times 10^5) = 2494500 \ J$$

• محاسبه $$Q_3$$: در این حالت، دما از صفر تا ۱۰۰ درجه سلسیوس تغییر کرده است اما فاز ثابت مانده است. بنابراین، از فرمول گرمای محسوس استفاده می‌کنیم:

$$Q_3 = m c \triangle T = 7.5 (4186) (+100 \ ^o C) = 3139500 \ J$$

• محاسبه $$Q_4$$: در این حالت، دما ثابت است اما فاز تغییر کرده است (مایع به بخار). بنابراین، از فرمول گرمای نهان تبخیر استفاده می‌کنیم:

$$Q_4 = m L_V = 7.5 (22.6 \times 10^5) = 16950000 \ J$$

• محاسبه $$Q_5$$: در این حالت، دما از ۱۰۰ تا ۲۰۰ درجه سلسیوس افزایش یافته است اما فاز ثابت مانده است. بنابراین، از فرمول گرمای محسوس استفاده می‌کنیم:

$$Q_5 = m c \triangle T = 7.5 (2010) (+1000 \ ^o C) = 1507500 \ J$$

مقدار کل انرژی برابر حاصل جمع پنج انرژی محاسبه شده در بالا است:

$$Q_T = Q_1 + Q_2 + Q_3 + Q_4 + Q_5 \\ Q_T = 24567000 \ J$$

اندازه‌ گیری گرمای نهان ویژه یخ

تاکنون با گرمای نهان، انواع و تفاوت آن با گرمای محسوس آشنا شدیم. در ادامه، آزمایشی ساده انجام و گرمای نهان یخ را اندازه می‌گیریم.

هدف آزمایش

برای تبدیل یخ به آب یا ذوب شدن یخ به انرژی نیاز است. در این آزمایش گرمای نهان ذوب یخ، انرژی لازم بر واحد گرم بری ذوب یخ، را اندازه می‌گیریم. این انرژی از لیوانی آب گرم گرفته خواهد شد. مقدار آب و دمای آن قبل از اضافه کردن یخ به آن و پس از ذوب یخ، اندازه گرفته می‌شوند. از داده‌های به‌دست آمده، برای تعیین گرمای نهان ذوب یخ استفاده خواهیم کرد.

انجام آزمایش

برای انجام این آزمایش، مرحله‌های زیر را به ترتیب انجام می‌دهیم:

مرحله اول

در ابتدا، مقداری یخ تهیه می‌کنیم و آن‌ها را داخل ظرفی در دمای اتاق،‌ قرار می‌دهیم. پس از گذشت زمانی در حدود ۲۰ دقیقه، یخ شروع به ذوب شدن خواهد کرد. دمای یخ داخل یخچال فریزر زیر دمای انجماد است. برای انجام این آزمایش، پس از بیرون آوردن تکه‌های یخ از فریزر و قرار دادن آن‌ها در ظرف، صبر می‌کنیم تا دمای یخ به صفر درجه سلسیوس برسد و شروع به ذوب شدن کند.

مرحله دوم

در حدود ۲۰۰ تا ۲۵۰ میلی‌لیتر آب گرم (دمای ۴۰ درجه سلسیوس) را داخل فلاسک یا لیوانی از جنس استایروفوم می‌ریزیم. دلیل این کار، کمینه کردن انتقال گرما بین آب با دمای بالاتر و محیط اطراف است. مقدار آب اضافه شده به فلاسک و دمای آن را قبل از اضافه کردن یخ، اندازه می‌گیریم.

مرحله سوم 

در این مرحله، یک یا دو تکه یخ را به آب اضافه می‌کنیم و مخلوط آب و یخ را با استفاده از دماسنج، تا ذوب شدن کامل یخ، هم می‌زنیم. پس از ذوب شدن کامل یخ، مقدار و دمای آب را اندازه می‌گیریم. دو اتفاق ممکن است رخ دهد:

1.  دمای اندازه‌گیری شده کمتر یا نزدیک دمای انجماد یخ باشد.
2. تمام یخ ذوب نشده باشد.

در صورت بروز هر یک از رخدادهای بالا، آزمایش را باید دوباره تکرار کنیم. در این حالت، یا از یخ کمتر یا از آب بیشتری استفاده می‌کنیم.

مرحله چهارم

پس از ذوب شدن تمام یخ، حجم آب موجود در فلاسک افزایش یافته است. بنابراین، حجم آن را با استفاده از استوانه مدرج اندازه می‌گیریم. حجم جدید بیشتر از حجم اولیه آب خواهد بود، زیرا یخ ذوب شده نیز به آن اضافه شده است. از آنجایی که چگالی آب برابر یک گرم بر میلی‌لیتر یا یک گرم بر سانتی‌متر مکعب است، رابطه‌ای یک به یک بین حجم آب اندازه‌گیری شده بر حسب میلی‌لیتر و جرم آن بر حسب گرم وجود دارد. تفاوت بین حجم‌های اولیه و نهایی برابر جرم یخ ذوب شده است.

آزمایش را حداقل یک بار دیگر با استفاده از مقدار متفاوتی آب و یخ تکرار می‌کنیم.

تحلیل داده‌ها 

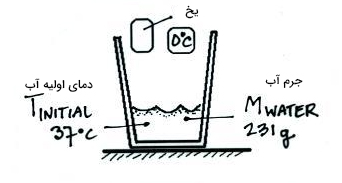
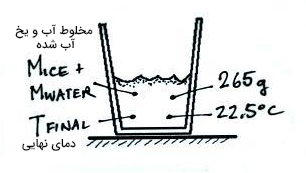
شرایط آزمایش در ابتدا را در تصویر زیر مشاهده می‌کنید.

• $$T_{initial}$$ دمای اولیه آب قبل از اضافه شدن یخ به آن است.
• $$M_{water}$$ جرم آبِ گرم است. به این نکته توجه داشته باشید که جرم آب از اندازه‌گیری حجم آن به‌دست می‌آید.
• دمای اولیه آب را صفر درجه سلسیوس در نظر می‌گیریم. زیرا یخ را پس از خارج کردن از فریزر در کاسه می‌ریزیم و تا رسیدن دمای آن به صفر درجه سلسیوس صبر می‌کنیم.

همان‌طور که در تصویر زیر دیده می‌شود، یخ را به آب گرم اضافه و تا ذوب شدن کامل آن صبر می‌کنیم. در این مرحله، یخ به طور کامل ذوب و از حالت جامد به مایع تبدیل می‌شود، اما دمای آن هنوز صفر درجه سلسیوس است. با توجه به مطالب گفته شده در بالا، تغییر فاز از حالت جامد به مایع در دمای ثابت را گرمای نهان ذوب می‌نامیم.

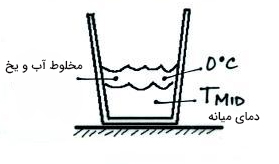
مقدار انرژی مورد نیاز برای ذوب یخ در دمای ثابت برابر است با:

$$\triangle E = M_{ice} \times L_{ice}$$

یخ انرژی گرمایی مورد نیاز برای ذوب شدن را از آب گرم دریافت می‌کند. در اثر این تبادل انرژی گرمایی بین یخ و آب، آب گرما از دست می‌دهد و دمای آن از دمای $$T_{initial}$$ به دمای $$T_{mid}$$ کاهش می‌یابد. مقدار انرژی آزاد شده توسط آب با استفاده از رابطه زیر به‌دست می‌آید:

$$\triangle E = M_{water} \times c_{water} \times (T_{initial} - T_{mid})$$

به این نکته توجه داشته باشید که مقدار این انرژی را محاسبه نمی‌کنیم، زیرا دمای $$T_{mid}$$ را نمی‌دانیم. انتقال گرما از آب با دمای بالاتر به یخِ آب شده در دمای صفر درجه سلسیوس ادامه می‌یابد. انتقال گرما تا رسیدن به دمای تعادل یعنی $$T_final$$ ادامه خواهد یافت.

آب برای رسیدن به دمای نهایی یا تعادل، مقدار دیگری انرژی گرمایی از دست می‌دهد:

$$\triangle E = M_{water} \times c_{water} \times (T_{mid} - T_{final})$$

انرژی لازم برای گرم کردن یخ ذوب شدن و افزایش دمای آن به دمای نهایی برابر است با:

$$\triangle E = M_{ice} \times c_{water} \times (T_{final} - 0 \ ^oC)$$

اکنون تمام قسمت‌ها را با یکدیگر ترکیب می‌کنیم. انرژی گرمایی دریافت شده از آب گرم دو کار انجام خواهد داد:

1. ذوب کردن تمام یخ در دمای ثابت صفر درجه سلسیوس
2. گرم کردن یخ آب شده و افزایش دمای آن از صفر به دمای تعادل

انرژی کل آزاد شده توسط آب برابر است با:

$$\triangle E = M_{water} \times c_{water} \times (T_{initial} - T_{final})$$

تمام آزمایش را در فلاسک انجام می‌دهیم، بنابراین به راحتی فرض می‌کنیم که تمام انرژی آزاد شده توسط آب گرم صرف ذوب یخ و گرم کردن آن شده است. به بیان دیگر، تبادل انرژی گرمایی با محیط اطراف را صفر در نظر می‌گیریم. با جمع انرژی گرمایی نهان یخ به هنگام ذوب شدن و انرژی جذب شده توسط یخِ آب شده برای افزایش دما، داریم:

$$\triangle E _ {used}= M_{ice} \times L + M_{ice} \times c_{ice} \times (T_{final} - 0 \ ^o C)$$

در مطالب بالا گفتیم، که بر طبق قانون پایستگی انرژی، انرژی گرمایی آزاد شده برابر انرژی گرمایی جذب شده است:

$$M_{water} \times L \times (T_{initial} - T_{final}) = M_{ice} \times L + M_{ice} \times c_{ice} \times (T_{final} - 0 \ ^o C)$$

گرمای ویژه آب برابر $$1 \ \frac{cal}{gm \ ^oC}$$ است. داده‌های زیر را اندازه گرفته‌ایم:

1. جرم آب
2. جرم یخ
3. دمای اولیه
4. دمای نهایی

با قرار دادن داده‌های بالا در رابطه به‌دست آمده، گرمای نهان یخ را محاسبه می‌کنیم.

$$M_{water} = 231 \ g \\\\\ M_{ice} = 265 \ g - 231\ g = 34 \ g \\ T_{initial} = 34 \ ^oC\\ T_{final} = 22.5 \ ^o C \\ 231 \ g \times 1 \ \frac{cal}{g \ ^o C} (37 \ ^oC - 22.5 \ ^oC) = 34 \ g\times L + 34 \ g \ \times 1 \frac{cal}{g \ ^o C} \times (22.5 \ ^o C- 0 \ ^o C) \\ 3349.5\ cal = 34 \ g \times L \\ L = 76 \ \frac{cal}{g}$$

مقدار گرمای نهان محاسبه شده برای یخ، ۸۰ کالری بر گرم است. بنابراین، عدد به‌دست آمده به عدد محاسبه شده برای گرمای نهان ذوب یخ بسیار نزدیک است.

گرمای نهان ذوب فلزات

گرمای نهان ذوب برخی از فلزات در جدول زیر نشان داده شده است:

جمع‌بندی

در این مطلب، در مورد گرمای نهان و انواع و تفاوت آن با گرمای محسوس صحبت کردیم. همچنین، با استفاده از آزمایشی ساده چگونگی اندازه‌گیری گرمای نهان یخ را توضیح دادیم.