فرادرسآموزش مثلثات — مجموعه مقالات جامع وبلاگ فرادرس
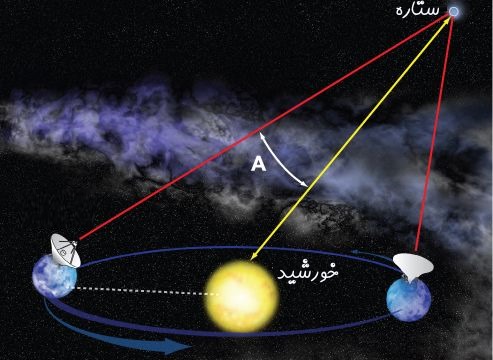
ریاضیات طرحی است که در آن تصویری از رخداد‌های طبیعت وجود دارد. با استفاده از این طرح می‌توان آینده یک جسم در حال سقوط را پیش‌بینی کرده یا یک ماشین طراحی کرد. یکی از ستون‌های اصلی ریاضی، مثلثات است. این بخش از ریاضیات به بررسی روابط طول‌ها و زاویه‌ها در مثلث می‌پردازد. جالب است بدانید از روابط مثلثاتی در ناوبری، سیستم‌های ماهواره‌ای و حتی در محاسبه فاصله میان‌ستاره‌ای استفاده می‌شود.
با توجه به اهمیت این مبحث، مجموعه مقالاتی در وبلاگ فرادرس و مرتبط با مثلثات منتشر شده که در این قسمت به طور خلاصه آن‌ها را معرفی می‌کنیم.
مثلثات چیست؟
مثلثات به بخشی از ریاضیات گفته می‌شود که به ارتباط میان طول‌ها و زوایا در اشکال هندسی می‌پردازد.
برای تعریف مفاهیم پایه‌ای مثلثات از مثلث قائم الزاویه استفاده می‌شود. در ابتدا اضلاع یک مثلث قائم الزاویه را مطابق با شکل زیر در نظر بگیرید.
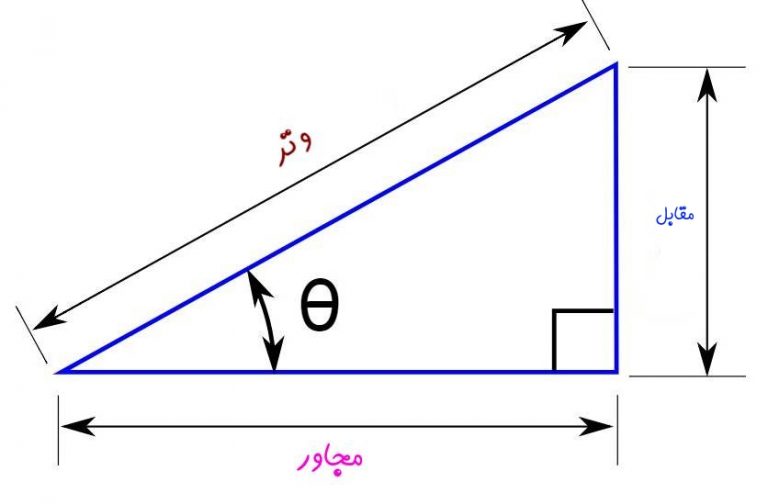
با توجه به مثلث فوق، سه نسبت مثلثاتی اصلی به صورت زیر تعریف می‌شوند.
اعمال ریاضی در مثلثات
بدیهی است که توابع مثلثاتی خانواده محبوبی در جامعه ریاضیات محسوب می‌شوند. دلیل این محبوبیت حضور فعال این خانواده در بسیاری از مسائل ریاضی و فیزیک است.
برای نمونه در حرکت پرتابی، اگر جسمی با زاویه θ پرتاب شود، ارتفاع جسم در هر لحظه با استفاده از رابطه زیر بدست می‌آید.
$$ \large y ( t ) = - { 1 \over 2 } { g t ^ 2 } + V _ 0 t \sin { \theta } $$
همان‌طور که می‌بینید در رابطه فوق از سینوس یا همان فرزند ارشد مثلثات استفاده شده است. حال اگر از رابطه فوق مشتق بگیرید، سرعت عمودی جسم پرتاب شده مطابق با رابطه زیر بدست می‌آید.
$$ V _ y ( t ) = \large -g t + V _ 0 \sin \theta $$
در رابطه فوق $$\theta $$ ثابت بود. اما در برخی از امکان دارد زاویه در یک رابطه متغیر بوده، در نتیجه نیاز باشد از تابعی مثلثاتی مشتق یا انتگرال گرفته شود.
کاربرد‌های مثلثات
همان‌طور که در بالا نیز بیان شد، مثلثات در بسیاری از مسائل ریاضی و فیزیک کاربرد دارد.
با توجه به گستردگیِ کاربرد مثلثات، نمی‌توان ادعا کرد که مقالات فوق تمامی موضوعات مرتبط با آن را پوشش داده؛ لذا مطالب مرتبط با مثلثات مرتبا به روزرسانی شده و در تلاش هستیم تا شعاع بیشتری از کاربرد‌ها و مفاهیم این مفهوم اساسی در ریاضیات را خدمت شما خواننده گرامی ارائه دهیم.
در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی آموزش‌های زیر نیز به شما پیشنهاد می‌شود:
- مجموعه آموزش‌های ریاضی و فیزیک
- مجموعه آموزش‌های دروس دبیرستان
- انتگرال گیری جزء به جزء — به زبان ساده
- روش نیوتن — به زبان ساده
- فهرست کامل مطالب ریاضی وبلاگ فرادرس
^^
با سلام و خسته نباشید خدمت کارکنان زحمتکش فرادرس. ببخشید اگر براتون مقدور هست یه کورس آموزشی جامع مثلثات بگذارید. با توجه به اهمیت این مبحث به نظر بنده خیلی ضروریه