مدل رشد جمعیت — به زبان ساده

رشد جمعیت یک فرایند پویا و دینامیکی است که می‌توان آن را با معادلات دیفرانسیل به خوبی توصیف کرد. در این آموزش، چند مدل رشد جمعیت را معرفی خواهیم کرد که توسط اقتصاددانان و فیزیکدانان مختلف ارائه شده است.

مدل رشد جمعیت مالتوس

ساده‌ترین مدل رشد جمعیت در سال ۱۷۰۹ توسط دانشمند انگلیسی، توماس رابرت مالتوس (Thomas Robert Malthus) ارائه شد. این مدل، رشد نمایی جمعیت را نشان می‌دهد و با معادله دیفرانسیل زیر توصیف می‌شود:

$$ \large \frac { { d N } } { { d t } } = a N $$

فیلم آموزش معادلات دیفرانسیل با میپل Maple در فرادرس

کلیک کنید

که در آن، $$\alpha$$ نرخ رشد (پارامتر مالتوس) است. جواب این معادله، تابع نمایی زیر است:

$$ \large N \left ( t \right ) = { N _ 0 } { e ^ { a t } } $$

که در آن، $$N_0$$ جمعیت اولیه را نشان می‌دهد.

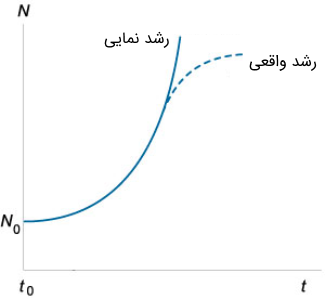
مدل رشد جمعیت ساده مالتوس به خوبی فاز اول رشد را توصیف می‌کند (برای وقتی که به دور از محدودیت‌هایش است). البته، دقت مدل نمایی در یک مرحله بعد، به دلیل اشباع یا اثرات غیرخطی کاهش می‌یابد (شکل ۱).

مدل لجستیک

این دسته از مدل‌های جمعیت توسط پیر فرانسوا فیرهلست (Pierre Francois Verhulst) در سال ۱۸۳۸ پیشنهاد شد. این مدل، مدل لجستیک (Logistic Model) نامیده می‌شود و به فرم معادله دیفرانسیل زیر است:

$$ \large \frac { { d N } } { { d t } } = a N \left ( { 1 – \frac { N } { M } } \right ) $$

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

که در آن، $$M$$ حداکثر اندازه جمعیت را نشان می‌دهد.

سمت راست این معادله به صورت زیر است:

$$ \large a N – \frac { { a { N ^ 2 } }} { M } $$

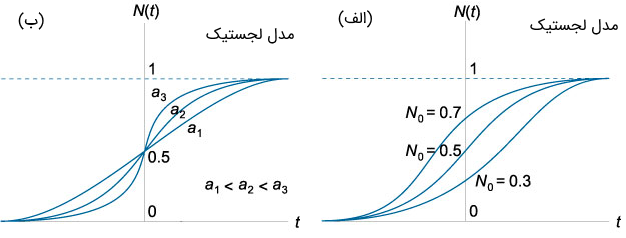
که جمله اول آن نشان دهنده رشد جمعیت است و جمله دوم، این رشد را به دلیل کمبود منابع در دسترس و سایر دلایل محدود می‌کند (شکل ۲ الف و ب).

مدل رشد جمعیت لجستیک جواب دقیق دارد و این جواب به صورت زیر است:

$$ \large { \frac { { d N } } { { d t } } = a N \left ( { 1 – \frac { N } { M } } \right ) , \; \; } \Rightarrow { \int { \frac { { d N } } { { N \left ( { 1 – \frac { N } { M } } \right ) } } } = \int { a d t } . } $$

انتگرالده انتگرال سمت راست را می‌توان با استفاده از روش تجزیه به کسرهای جزئی به دست آورد:

$$ \large \begin{align*}
& { \frac { 1 } { { N \left ( { 1 – \frac { N } { M } } \right ) } } } = { \frac { A } { N } + \frac { B } { { 1 – \frac { N } { M } } } , \; \; } \\ & \Rightarrow
{ { \frac { 1 } { { N \left ( { 1 – \frac { N } {M } } \right ) } } } = { \frac { { A \left ( { 1 – \frac { N} { M } } \right ) + B N } } { { N \left ( { 1 – \frac { N } { M } } \right ) } } , \; \; } } \\ & \Rightarrow
{ 1 \equiv A – A \frac { N } { M } + B N , \; \; } \Rightarrow
{ \left \{ { \begin {array} { * { 20 } { l } }
{ A = 1 } \\
{ B = \frac { 1 } { M } }
\end {array} } \right . . }
\end {align*} $$

در نتیجه، انتگرال سمت چپ برابر است با:

$$ \large \begin{align*}
\int { \frac { { d N } } { { N \left ( { 1 – \frac { N } { M } } \right ) } } } & = { \int { \left ( { \frac { 1 } { N } + \frac { { \frac { 1 } { M } } } { { 1 – \frac { N } { M } } } } \right ) d N } } = { \int { \frac { { d N } } { N } } + \int { \frac{ { d \left ( { \frac { N } { M } } \right ) } } { { 1 – \frac { N } { M } } } } } \\ & = { \ln \left | N \right | – \ln \left | { 1 – \frac { N } { M } } \right | } = { \ln \left | { \frac { N } { { 1 – \frac { N } { M } } } } \right | } = { \ln \frac { N } { { 1 – \frac {N } { M } } } .}
\end {align*} $$

بنابراین، جواب عمومی معادله دیفرانسیل لجستیک به صورت زیر خواهد بود:

$$ \large \begin{align*}
& { \ln \frac { N } { { 1 – \frac { N } { M } } } } = { a t + \ln C , \; \; } \Rightarrow { { \ln \frac { N } { { 1 – \frac { N } { M } } } } = { \ln { e ^ { a t } } + \ln C , \; \; } } \\ & \Rightarrow { \ln \frac { N } { { 1 – \frac { N } { M } } } = \ln C { e ^ { a t } } , \; \; } \Rightarrow { \frac { N } { { 1 – \frac { N } { M } } } = C { e ^ { a t} } . }
\end {align*} $$

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

از معادله جبری بالا می‌توان $$N$$ را به دست آورد:

$$ \large \begin {align*}
N & = C { e ^ { a t } } – \frac { N } { M } C { e ^ { a t } } , \; \; \Rightarrow { N \left ( { 1 + \frac { 1 } { M } C { e^ {a t } } } \right ) = C { e ^ { a t } } , \; \; } \\ & \Rightarrow { N = \frac { { C { e ^ { a t } } } } { { 1 + \frac { 1 } { M} C {e ^ { a t} } } } } = { \frac { { C M { e ^ { a t } } } } {{ M + C { e ^ { a t } } } } . }
\end {align*} $$

ثابت $$C$$ نیز از شرایط اولیه $$ N\left( {t = 0} \right) = {N_0} $$ به دست می‌آید:

$$ \large { { N _ 0 } = \frac { { C M \cdot 1 } } { { M + C } } , \; \; } \Rightarrow { C M = { N _ 0 } M + C { N_ 0 } , \; \; } \Rightarrow { C = \frac { { { N _ 0 } M } } { { M – { N _ 0 } } } . } $$

با جایگذاری این مقدار در جواب عمومی، خواهیم داشت:

$$ \large \begin {align*}
N \left ( t \right ) & = \frac { { \frac { { {N _ 0 } { M ^ 2 } { e ^ { a t } }} } { { M – { N _ 0 } } } } } { { M + \frac { { { N _ 0 } M { e ^ { a t } } } } { { M – { N _ 0 } } } } } = { \frac { { { N _ 0 } { M ^ 2 } { e ^ { a t } } } } { { { M ^ 2} – { N _ 0 } M + { N _ 0 } M { e ^ { a t } } } } } \\ & = { \frac { { { N _ 0 } M { e ^ { a t } } } } { { M – { N _ 0 } + { N _ 0 } { e ^ { a t } } } } } = { \frac { { { N _ 0 } M } } { { { N _ 0 } + \left ( { M – { N _ 0 } } \right ) { e ^ { – a t } } } } . }
\end {align*} $$

نمودار تابع لجستیک نمای زیبایی دارد. شکل ۲ (الف) چند منحنی لجستیک را برای مقادیر مختلف $$N_ 0 $$ نشان می‌دهد. شکل ۲ (ب) نیز، نشان می‌دهد که چگونه شکل منحنی با تغییرات نرخ رشد $$a $$ دچار تغییر می‌شود.

مدل رشد جمعیت هیپربولیک

مدل‌هایی که در بخش‌های قبل معرفی کردیم، در تحلیل فرایندهای جمعیتی در بازه قرن مفید هستند. اما اگر بخواهیم رشد جمعیت را برای چندین هزار سال بررسی کنیم (شکل ۳)، می‌بینیم که رشد انفجاری اصلی از ۲ تا ۵ میلیارد نفر، در پنجاه سال گذشته رخ داده است. این نوع وابستگی مشابه یک منحنی هیپربولیک یا هذلولوی است. یک مدل رشد جمعیت هیپربولیک که توسط چند دانشمند (فون فورستر (von Forster) در ۱۹۶۰، فون هوستر (von Hoster) در ۱۹۷۵ و  شکلوفسکی (Shklovskii ) در ۱۹۸۰) معرفی شد، به فرم زیر است:

$$ \large { N \left ( t \right ) = \frac { C } { { { T _ 1 } – t } } } = { \frac { { 2 0 0 } } { { 2 0 2 5 – t } } \, \left ( \text {bln.} \right ) } $$

فیلم آموزش هندسه دیفرانسیل برای عمران و نقشه برداری در فرادرس

کلیک کنید

همان‌طور که این مدل نشان می‌دهد، جمعیت جهان در سال ۲۰۲۵ به بینهایت می‌رسد.

با این حال، دینامیک رشد واقعی نشان می‌دهد که گذار یا انتقال جمعیت بعد از مرحله رشد انفجاری دنبال می‌شود. این حالت جدید با کاهش باروری و مرگ‌ومیر مشخص می‌شود. چنین انتقال یا گذاری قبلاً‌ در بسیاری از کشورهای توسعه یافته رخ داده است. در نتیجه گذار جمعیتی، رشد جمعیت متوقف شده و حتی ممکن است سقوط کند. کل جمعیت جهان در آغاز قرن ۲۱ وارد مرحله انتقال جمعیتی شده است.

چنین پویایی جمعیت پیچیده‌ای را می‌توان به خوبی با استفاده از معادلات دیفرانسیل بیان کرد. مدلی از این نوع، اخیراً در سال ۱۹۹۷ توسط دانشمند روسی، سرگئی کاپیتسا (Sergey Kapitsa) ارائه شد. کاپیتسا انفجار جمعیت را با معادله زیر توصیف کرد:

$$ \large \frac { { d N } } { { d t } } = \frac { C } { { { { \left ( { { T _ 0 } – t } \right ) } ^ 2 } + { \tau ^ 2 } } } $$

که در آن، $$T_0$$، $$ C $$ و $$\tau$$ پارامترهای تقریب معینی هستند. این معادله دیفرانسیل دارای جواب دقیق زیر است:

$$ \large { N \left ( t \right ) } = { \frac { C } { \tau } \text {arccot} \, \frac { { { T _ 0 } – t } } { \tau } . } $$

تابع بالا رشد جمعیت انفجاری را با پارامترهای $$ C = 1.86 \times {10^{11}}$$، $${T_0} = 2007$$ و $$ \tau = 42 $$ به خوبی توصیف می‌کند. همچنین، این مدل رشد جمعیت مرحله انتقال جمعیتی را وقتی که رشد جمعیت به اشباع می‌رسد، پوشش می‌دهد (شکل ۳).

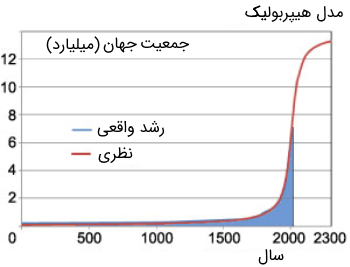
براساس این مدل رشد جمعیت ، جمعیت کل جهان در سال‌های ۲۲۰۰ تا ۲۳۰۰ به ۱۲ میلیارد نفر خواهد رسید.