مخروط، کره و استوانه — حجم و مساحت اشکال هندسی به زبان ساده

در تصویر فوق به ترتیب از راست به چپ یک استوانه، کره و مخروط را می‌بینیم. در این نوشته با این حجم‌های هندسی بیشتر آشنا شده و فرمول محاسبه حجم و مساحت آنها را معرفی می‌کنیم. البته در این لینک فرمول‌های مربوط به محاسبه این اشکال ارائه شده که در زمانی اندک می‌توانید آن‌‌ها را فرا بگیرید.

حجم یک مخروط نسبت به حجم استوانه

ار آنجا که می‌توان یک مخروط را در فضای داخل یک استوانه جای داد، برای محاسبه حجم مخروط یا استوانه از فرمول‌های زیر استفاده می‌کنیم:

فرمول‌های حجم مخروط‌ و استوانه‌ بسیار شبیه هم هستند:

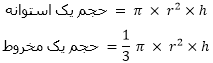
بنابراین حجم یک مخروط دقیقا یک سوم (1/3) حجم استوانه‌ای با ‌قاعده و ارتفاع برابر خودش است. با اندکی تلاش می‌توانید تجسم کنید که چگونه می‌توان 3 مخروط را داخل یک استوانه جای داد.

حجم یک کره نسبت به حجم استوانه

این بار یک استوانه را به دور یک کره محیط کنید. اکنون برای اینکه کره به خوبی درون استوانه محاط شود باید استوانه‌ای به ارتفاع 2r درست کنیم.

بنابراین برای استوانه‌ای با حجم 2، می‌توان کره‌ای با حجم 4/3 محاط کرد. یا بصورت ساده‌تر می‌توان گفت حجم کره 2/3 حجم استوانه است.

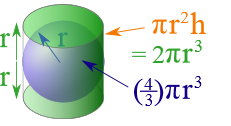
نتیجه

بنابراین می‌توان این‌گونه استنباط کرد که یک مخروط و یک کره با هم یک استوانه را ایجاد می‌کنند. بدین منظور باید فرض کنید که آن‌ها کاملا با یکدیگر متناسب هستند، بنابراین رابطه h = 2r برقرار است.

رابطه‌های ریاضی شگفت‌انگیز هستند! اینک سوالی که پیش می‌آید این است که چه رابطه‌ای بین حجم یک مخروط و حجم نصف یک کره (نیم‌کره) وجود دارد؟ مشخص است که حجم نیم‌دایره نصف حجم دایره است. بنابراین باتوجه به این که نصف 2/3 برابر با 1/3 است، پس حجم نیم‌کره و مخروط با هم برابر هستند.

مساحت سطح

در ادامه فرمول محاسبه مسات سطحی این سه حجم هندسی را ارائه کرده‌ایم. آیا می‌توانید حدس بزنید مساحت سطح این سه شکل چه رابطه‌ای دارند؟

با مقایسه مساحت سطح کره و استوانه به همان نسبت 2/3 دست یافتیم. اما چنین نظری در مورد مخروط صدق نمی‌کند. برای آشنایی با نحوه محاسبه مساحت سطح کره، پیشنهاد می‌کنیم مطلب «مساحت کره و محاسبه آن | به زبان ساده» را مطالعه کنید.