سینوس، کسینوس و تانژانت یک زاویه – به زبان ساده

مثلثات به بخشی از ریاضیات اطلاق می‌شود که ارتباط میان زوایا و طول‌ها را مورد بررسی قرار می‌دهد. در این مطلب از مجله فرادرس، سه مفهومِ مهم سینوس، کسینوس و تانژانت را به زبان ساده تعریف خواهیم کرد. احتمالا با حذف این سه‌ مفهوم از علم ریاضی، بخش اعظمی از فیزیک نیز بایستی حذف شود! البته در ریاضیات نیز این مفاهیم به دفعات مشاهده می‌شوند. برای نمونه پاسخ‌های یک معادله درجه ۳ بر حسب سینوس کسینوس ضرایب معادله بدست می‌آیند.

مثلث قائم‌الزاویه

مثلث قائم‌الزاویه به مثلثی گفته می‌شود که یکی از زوایای آن ۹۰ درجه باشد. در چنین مثلثی دو ضلع عمود بر هم وجود دارد و ضلع سوم انتهای این دو را به یکدیگر متصل می‌کند.

سینوس، کسینوس و تانژانت مفاهیمی هستند که در مثلث قائم‌الزاویه معنا و مفهوم پیدا می‌کنند. جهت توضیح روابط مربوط به این مفاهیم، در ابتدا مثلثی قائم‌الزاویه را مطابق با شکل زیر در نظر بگیرید.

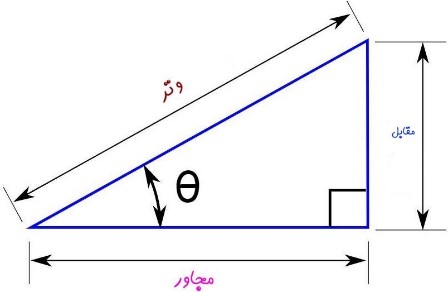
جهت درک بهتر مفاهیم، اجزا یک مثلث قائم‌الزاویه را مطابق با زیر نام‌گذاری می‌کنیم:

• ضلع مقابل: ضلع قرار گرفته مقابل زاویه θ
• ضلع مجاور: ضلع قرار گرفته کنار زاویه θ
• وتر: بزرگ‌ترین ضلع مثلث قائم‌الزاویه

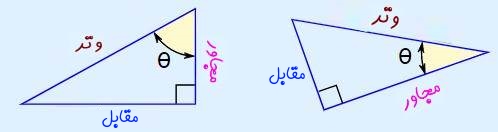
شکل فوق دو مثلث قائم‌الزاویه و اجزاء آن را نشان می‌دهد.

سینوس، کسینوس و تانژانت

مفاهیم سینوس، کسینوس و تانژانت برابر با نسبت اضلاع یک مثلث قائم‌الزاویه تعریف می‌شوند.

فیلم آموزش هندسه ۲ – پایه یازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

در زیر مثلثی قا‌ئم‌الزاویه و توابع مثلثاتی مربوط به آن تعریف شده‌اند.

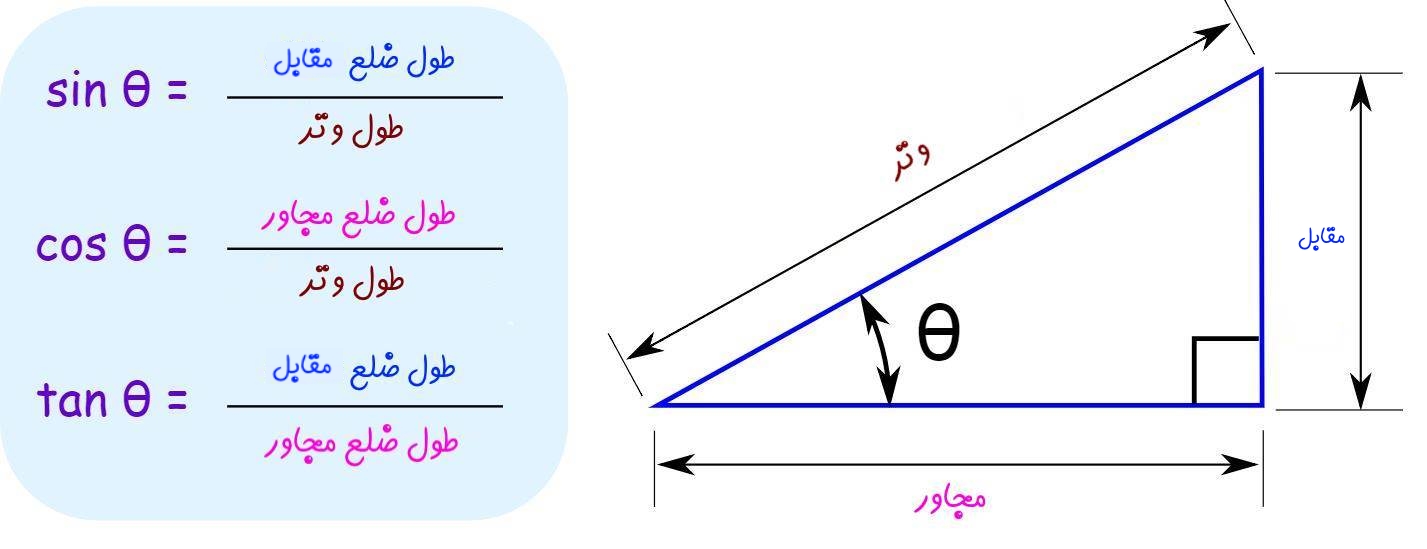
سینوس، کسینوس و تانژانت به‌ترتیب با نماد‌های cos ،sin و tan نمایش داده می‌شوند. توجه داشته باشید که برای یک زاویه‌ θ ثابت، این مقادیر ثابت هستند؛ دلیل این امر، افزایش همزمان صورت و مخرج آن‌ها است. در ادامه مثالی ذکر شده که جهت درک بهتر این مفاهیم، مطالعه آن ضروی است.

مثال ۱

مثلثی را مطابق با شکل زیر در نظر بگیرید.

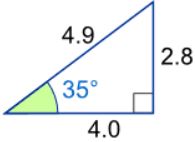
با توجه به شکل فوق، مقادیر sin 35⁰ ،cos 35⁰ وtan 35⁰ را بدست آورید.

طبق تعریف انجام شده در بالا، مقدار سینوس ۳۵ درجه (sin 35⁰) برابر است با:

هم‌چنین مقادیر $$\cos 35 ^ { \circ }$$ و $$\tan 35 ^ { \circ }$$ نیز برابرند با:

ماشین‌ حساب‌های مهندسی و علمی نیز قابلیت محاسبه مقادیر مثلثاتی - یا همان سینوس، کسینوس و تانژانت - را دارند.

البته توجه داشته باشید که یک زاویه را می‌توان در دو حالت رادیان یا درجه بیان کرد. برای نمونه ۳.۱۴ رادیان برابر با ۱۸۰ درجه است.

جهت به‌خاطر سپردن، می‌توانید از شکل‌های زیر استفاده کنید. در این اشکال، از فلش‌های صورتی رنگی استفاده شده که ابتدای آن اندازه ضلع قرار گرفته در صورت و انتهایش اندازه ضلعِ مخرجِ کسر را نشان می‌دهد.

توجه داشته باشید که مقادیر سینوس و کسینوس کمتر از ۱ و بیشتر از ۱- هستند؛ اما مقدار تانژانت می‌تواند از منفی بینهایت تا مثبت بینهایت تغییر کند.

مثال ۲

با توجه به شکل زیر، مقادیر سینو‌س، کسینوس و تانژانت زاویه ۳۰ درجه را بدست آورید.

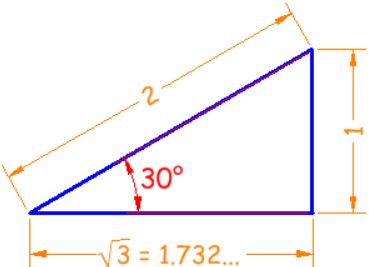
با توجه به طول‌های نشان داده شده در شکل فوق می‌توان گفت:

می‌توانید مقادیر به‌دست آمده در بالا را با استفاده از ماشین‌ حساب چک کنید.

مثال ۳

سینوس، کسینوس و تانژانت زاویه ۴۵ درجه را با توجه به شکل زیر بدست آورید.

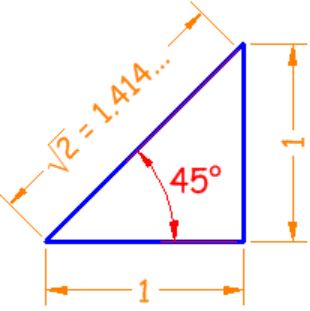
در زاویه ۴۵ درجه، مثلث، همزمان قائم‌الزاویه و متساوی‌ الساقین است؛ بنابراین طولِ اضلاع مجاور و مقابل با هم برابر هستند. از این رو همان‌طور که در ادامه نیز محاسبه شده مقادیر سینوس و کسینوس با هم برابر بوده و مقدار تانژانت نیز برابر با ۱ است. در حقیقت این مقادیر برابرند با:

در ادامه، مقدار توابع مثلثاتی برای زوایای پرکاربرد، در قالب جدول سینوس کسینوس تانژانت ذکر شده است. پیشنهاد می‌شود جدول مذکور را به خاطر بسپارید.

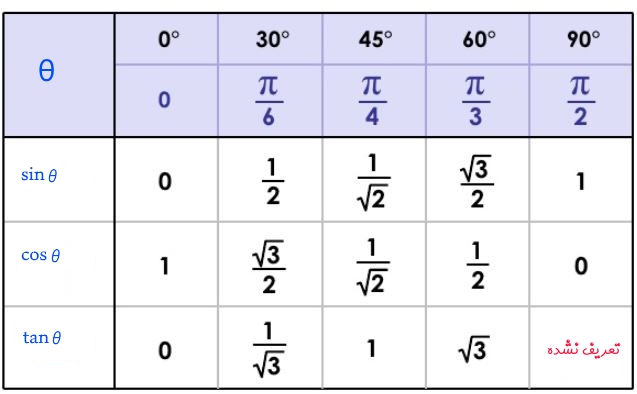
بدیهی است که حفظ کردن ۱۵ عدد به نظر دشوار می‌رسد؛‌ از این رو روشی را ارائه می‌دهیم که با استفاده از آن می‌توان مقادیر سینوس و کسینوس را محاسبه کرد. در نتیجه با داشتن این دو مقدار و تقسیم آن‌ها به یکدیگر، مقدار تانژانت نیز قابل محاسبه خواهد بود. انگشت کوچک تا شست را به ترتیب با اعداد ۰ تا ۴ نا‌مگذاری کنید. همانند شکل زیر، این انگشتان را به‌ترتیب در زوایای ۰، ۳۰، ۴۵، ۶۰ و ۹۰ درجه در نظر بگیرید.

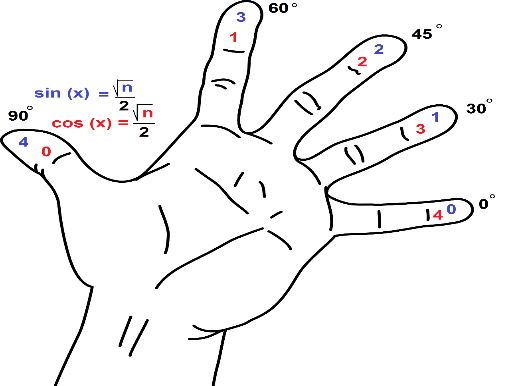
به‌منظور محاسبه سینوسِ یک زاویه، از شماره انگشت مرتبط با آن جذر گرفته و بر ۲ تقسیم کنید. برای نمونه فرض کنید می‌خواهید سینوس ۳۰ درجه را محاسبه کنید. همان‌طور که در شکل زیر نیز مشخص شده، انگشت شماره ۱ در زاویه ۳۰ درجه قرار دارد، بنابراین سینوس این زاویه برابر است با:

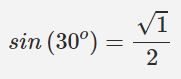
به‌منظور محاسبه کسینوس نیز دقیقا همین کار را به‌صورت عکس انجام دهید؛ یعنی شماره انگشت شست برابر با صفر و انگشت کوچک برابر با ۴ است. فرض کنید می‌خواهید کسینوس ۳۰ درجه را محاسبه کنید. همان‌گونه که در شکل فوق می‌بینید شماره ۳ در زاویه ۳۰ درجه قرار دارد (اعداد قرمز رنگ مربوط به محاسبه کسینوس هستند). در نتیجه کسینوس زاویه ۳۰ درجه برابر است با:

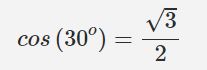
چرا این مفاهیم مهم هستند؟

به راستی چرا این‌ مفاهیم تعریف شده و دارای اهمیت‌اند؟ البته این مفاهیم دارای کاربرد‌های فراوانی هستند؛ اما اصلی‌ترین دلایل آن‌ها موارد زیر هستند.

• با دانستن زاویه یک کمیت می‌توان اندازه آن را یافت.
• با دانستن اندازه یک کمیت -برداری- می‌توان زاویه آن را یافت.

فیلم آموزش ریاضی 2 – پایه یازدهم علوم تجربی در فرادرس

کلیک کنید

شاید بیان بالا برای شما کمی گیج‌کننده باشد؛ از این رو پیشنهاد می‌کنیم که حتما مثال زیر را مطالعه فرمایید.

مثال ۴

با استفاده از مفهوم سینوس، اندازه d را در شکل زیر بیابید.

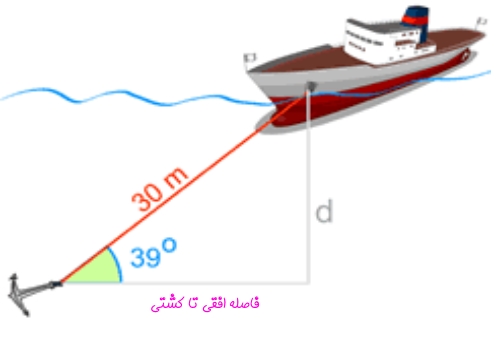
فرضیات و مجهول این مسئله به شرح زیر هستند:

• زاویه کابل با سطح افقی آب برابر با ۳۹ درجه است.
• طول کابل برابر با ۳۰ متر است.
• ?=d

همان‌طور که در شکل نیز مشخص شده می‌توان مثلث قائم‌الزاویه‌ای در نظر گرفت که در آن طولِ کابل برابر با وتر، فاصله d برابر با ضلع مقابل و فاصله افقی تا کشتی، برابر با ضلع مجاورِ زاویه ۳۹ درجه است.

در ابتدا با استفاده از ماشین‌ حساب سینوس زاویه ۳۹ درجه برابر با ۰.۶۲۹۳ بدست می‌آید. در حقیقت:

با ضرب کردن دو طرف رابطه بالا در عدد ۳۰، می‌توان گفت:

بنابراین اندازه d برابر با ۱۸.۸۸ متر بدست می‌آید.

دیگر توابع

توجه داشته باشید که در مثلثات توابع دیگری نیز وجود دارند که کمتر متداول هستند. این توابع سِکانت، کُسِکانت و کُتانژانت هستند که هرکدام از آن‌ها با استفاده از روابط زیر تعریف می‌شوند:

رابطه بالا می‌گوید:

• سکانت = معکوس کسینوس
• کسکانت = معکوس سینوس
• کتانژانت = معکوس تانژانت

آزمون سنجش یادگیری سینوس، کسینوس و تانژانت یک زاویه

در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث سینوس، کسینوس و تانژانت یک زاویه را با طرح سوال‌های چندگزینه‌ای می‌سنجیم. پس از جواب دادن به تمام سوال‌ها، نتیجه آزمون برای شما به نمایش درمی‌آید.

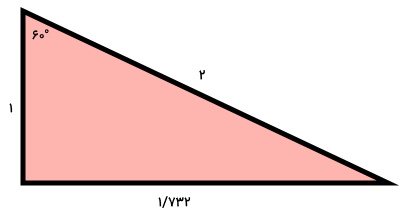
اندازه یکی زوایای مثلث قائم‌الزاویه زیر برابر با 60 درجه است. بر اساس اندازه‌های داده شده، کدامیک از گزینه‌های زیر، کسینوس این زاویه را نمایش می‌دهد؟

0/5

0/577

0/866

2

مشاهده گزینه صحیح

پاسخ تشریحی

بر اساس تعریف کسینوس در مثلث قائم‌الزاویه، داریم:

اندازه ضلع مجاور به زاویه تقسیم بر اندازه وتر = کسینوس یک زاویه

می‌خواهیم کسینوس زاویه 60 درجه را به دست بیاوریم. اندازه ضلع مجاور به این زاویه در مثلث قائم‌الزاویه برابر با 1 بوده و اندازه وتر برابر با 2 است. بنابراین:

$$\cos 60 ^ { \circ } = \frac { 1 } { 2 } = 0/5$$

در نتیجه کسینوس زاویه 60 درجه برابر با 0/5 است.

 

تانژانت زاویه 60 درجه در مثلث قائم‌الزاویه زیر چند است؟

0/5

0/577

0/866

1/732

مشاهده گزینه صحیح

پاسخ تشریحی

تانژانت یک زاویه در مثلث قائم‌الزاویه به صورت زیر تعریف می‌شود:

اندازه ضلع مقابل به زاویه تقسیم بر اندازه ضلع مجاور به زاویه = تانژانت زاویه

در این سوال، می‌خواهیم تانژانت زاویه 60 را به دست بیاوریم. اندازه ضلع مقابل به این زاویه برابر با 1/732 و اندازه ضلع مجاور به این زاویه برابر با 1 است. بنابراین، داریم:

$$\tan 60 ^ { \circ } = \frac { 1/732 } { 1 } = 1/732$$

در نتیجه، تانژانت زاویه 60 برابر با 1/732 است.

 

مثلث قائم‌الزاویه‌ای با وتری به اندازه 5 سانتی‌متر و ساق‌هایی به اندازه 3 و 4 سانتی‌متر را در نظر بگیرد. مقدار سینوس زاویه مقابل به ساق ۳ سانتی‌متری چند است؟

1/33

0/8

0/75

0/6

مشاهده گزینه صحیح

پاسخ تشریحی

برای شروع، مثلث قائم‌الزاویه مورد سوال را رسم می‌کنیم.

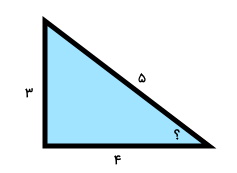
می‌خواهیم سینوس زاویه مشخص شده در تصویر بالا را به دست بیاوریم. برای این کار، زاویه مجهول را برابر با پارامتری مانند $$\theta$$ در نظر می‌گیریم و سپس ضلع مقابل به زاویه را بر وتر تقسیم می‌کنیم:

$$\sin \theta = \frac { 3 } { 5 } = 0/6$$

 

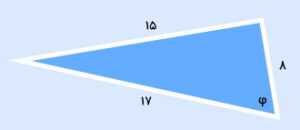
کسینوس زاویه $$\phi$$ در مثلث قائم‌الزاویه زیر چیست؟

2/125

1/875

0/47

0/8824

مشاهده گزینه صحیح

پاسخ تشریحی

کسینوس زاویه φ، از تقسیم اندازه ضلع مجاور به φ بر روی وتر به دست می‌آید:

$$\cos φ = \frac { 8 } { 17 } = 0/47$$

 

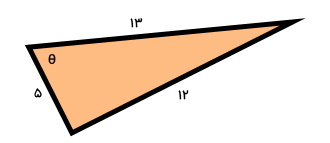
سکانت زاویه $$\theta$$ چند است؟

2/6

0/3846

2/4

1/083

مشاهده گزینه صحیح

پاسخ تشریحی

مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.

ورود / ثبت‌نام