متغیر تصادفی و توزیع کوشی (Cauchy Distribution) – به زبان ساده

براساس توزیع‌های آماری، می‌توان رفتار پدیده‌های تصادفی را شناخت. بسیاری از داده‌ها که مربوط به پدیده‌های تصادفی کسب و کار و داده‌های مالی و همینطور علوم آب (Hydrology) و فیزیک ذرات است، دارای توزیع کوشی (Cauchy Distribution) هستند. در نتیجه این توزیع از اهمیت خاصی برخوردار است. از طرف دیگر وجود خصوصیات جالب برای این توزیع، بسیاری از آماردانان را به سوی خود جلب کرده است.

از آنجایی که در این نوشتار از متغیر تصادفی و تابع احتمال صحبت به میان خواهد آمد بهتر است ابتدا مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال را مطالعه کرده باشید. همچنین مطالعه مطلب مربوط به توزیع نرمال و قضیه حد مرکزی و توزیع t-student نیز خالی از لطف نیست.

متغیر تصادفی و توزیع کوشی

این توزیع به افتخار دانشمند و ریاضیدان بزرگ فرانسوی، اگوستین کوشی (Augustin Cauchy) نام‌گذاری شده است. او در قرن ۱۷، به بررسی توابع ریاضیاتی پرداخت که از لحاظ شکل تابعی شبیه تابع احتمال کوشی هستند. در سال ۱۸۲۴، ریاضیدان بزرگ فرانسوی «پواسن» (Poisson) این تابع را به عنوان یک توزیع آماری برشمرد. او در مقاله‌ای نشان داد که واریانس برای داده‌هایی که دارای توزیع کوشی باشند، وجود ندارد. البته در فیزیک به علت تحقیقاتی مجزایی که «هنریک لورنتز» (Hendrik Lorentz) روی داده‌ها با توزیع کوشی انجام داد به توزیع لورنتز نیز شهرت دارد. به همین علت گاهی آن را به توزیع کوشی-لورنتز می‌خوانند.

توزیع کوشی، یکی از انواع «توزیع‌های پایدار» (Stable Distribution) است که تابع چگالی احتمال آن فرم بسته دارد. قابل ذکر است که توزیع نرمال نیز از گروه توزیع‌های پایدار است، به این معنی که ترکیب خطی از دو متغیر تصادفی با توزیع نرمال با پارامترهای مختلف، باز هم دارای توزیع نرمال و برحسب ترکیبی از پارامترهای آن‌ها است.

در بین توزیع‌های پایدار، توزیع نرمال (Normal Distribution)، «توزیع کوشی» (Cauchy Distribution)، «توزیع هولتس‌مارک» (Holtsmark Distribution) و «توزیع لوی» (Levy Distribution) دارای فرم بسته برای تابع چگالی احتمال هستند.

تابع چگالی احتمال متغیر تصادفی کوشی

X متغیر تصادفی با توزیع کوشی است اگر تابع چگالی احتمال آن به صورت زیر باشد:

$$\large \displaystyle f(x;\theta,\gamma )=P(x)={\frac {1}{\pi \gamma \left[1+\left({\frac {x-\theta}{\gamma }}\right)^{2}\right]}}$$

در این رابطه، $$\theta$$ پارامتر مکان و $$\gamma$$ پارامتر مقیاس گفته می‌شود. در این حالت می‌نویسیم $$X\sim Cauchy(\theta,\gamma)$$ و می‌خوانیم، X دارای توزیع کوشی با پارامتر مکان $$\theta$$ و پارامتر مقیاس $$\gamma$$ است. تکیه‌گاه این متغیر تصادفی همه اعداد حقیقی است.

گاهی برای محاسبه جرم احتمال می‌توان از رابطه‌ای که در زیر نوشته شده، نیز استفاده کرد.

$$\large f(x;\theta,\gamma )={1 \over \pi \gamma }\left[{\gamma ^{2} \over (x-\theta)^{2}+\gamma ^{2}}\right]$$

شکل تابع چگالی احتمال (Probability Density Function -PDF) برای توزیع کوشی در تصویر زیر دیده می‌شود.

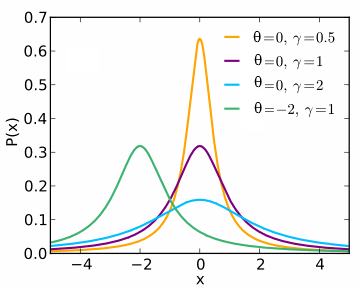
مشخص است که حداکثر این تابع در نقطه $$\theta$$ یعنی پارامتر مرکزی توزیع حاصل می‌شود. از طرفی در این توزیع با افزایش مقدار $$\gamma$$ گستردگی منحنی افزایش می‌یابد. به نوعی می‌توان پارامتر $$\gamma$$ را «نصف پهنا در نصف مقدار بیشینه» (Half Width at Half Maximum- HWHM) در نظر گرفت و دو برابر آن یعنی $$\gamma$$2 نیز نشان دهنده «پهنا در نصف مقدار بیشینه» (Full Width at Half Maximum- FWHM) است که در تصویر زیر دیده می‌شود.

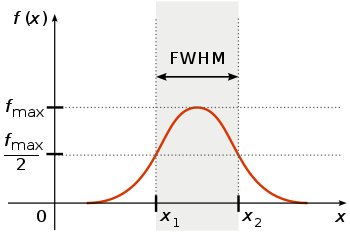
از طرفی پارامتر $$\gamma$$ را می‌توان نصف مقدار دامنه میان چارکی (Interquartile Range- IQR) نیز نامید. به این ترتیب فاصله بین چارک سوم و اول در این توزیع، دو برابر پارامتر مقیاس یعنی $$\gamma$$ در این توزیع است.

نکته: اگر مقدار پارامتر مرکزی برابر با صفر و پارامتر مقیاس نیز برابر با ۱ باشد، توزیع حاصل را کوشی استاندارد می‌نامند زیرا چنین توزیعی می‌تواند از تقسیم دو توزیع نرمال استاندارد مستقل ایجاد شود.در این حالت می‌نویسم $$X\sim Cauchy(0,1)$$ است.

در تصویر زیر مشخص است که توزیع کوشی استاندارد نسبت به توزیع نرمال استاندارد دارای دم‌های کلفت‌تری است. به این معنی که جرم احتمال در دم‌ها نسبت به توزیع نرمال استاندارد بیشتر است.

مقدار تابع توزیع احتمال تجمعی (Cumulative Distribution Function- CDF) برای این توزیع نیز براساس انتگرال روی تابع چگالی احتمال حاصل می‌شود. به این ترتیب داریم:

$$\large F_X(y)=P(X\leq y)=\int_{-\infty}^y f_x(x)dx=$$

$$\large {\frac {1}{\pi }}\arctan \left({\frac {x-\theta}{\gamma }}\right)+{\frac {1}{2}}$$

نمودار حاصل از تابع توزیع احتمال تجمعی برای این توزیع در تصویر زیر دیده می‌شود. مشخص است که با افزایش مقدار پارامتر $$\gamma$$ منحنی تابع توزیع تجمعی احتمال از حالت s بسته به s باز تبدیل می‌شود.

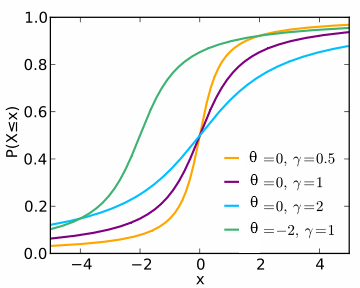
خصوصیات توزیع کوشی

با توجه به فرم تابع چگالی احتمال، امید ریاضی و واریانس برای متغیر تصادفی با توزیع کوشی وجود ندارد. بنابراین قضیه حد مرکزی را نمی‌توان برای این متغیر تصادفی به کار برد. به این معنی که مجموع n متغیر تصادفی مستقل و هم‌توزیع کوشی، نمی‌توانند برای مقدار‌های بزرگ n، دارای توزیع نرمال باشد.

فیلم آموزش متغیرهای تصادفی (الف) در آمار و احتمال مهندسی (مرور – تست کنکور ارشد) (رایگان) در فرادرس

کلیک کنید

ولی براساس نمودار و شکل تابع چگالی احتمال، مشخص است که «نما» (Mode) برای متغیر تصادفی با توزیع کوشی برابر با $$\theta$$ است. از طرفی با توجه به تقارن تابع چگالی احتمال، مشخص است که «میانه» (Median) نیز برای این متغیر تصادفی همان $$\theta$$ خواهد بود.

ارتباط با توزیع‌های دیگر

براساس تبدیلات و محاسباتی که بین متغیرهای تصادفی وجود دارد، می‌توان روابط زیر را بین توزیع کوشی و توزیع‌های دیگر مشخص کرد.

• اگر U و V دو متغیر تصادفی با توزیع نرمال استاندارد باشند، آنگاه نسبت آن‌ها دارای توزیع کوشی استاندارد است.
• اگر $$X_1,X_2,\cdots,X_n$$ متغیرهای تصادفی iid (مستقل و هم‌توزیع) با توزیع کوشی استاندارد باشند، آنگاه میانگین آن‌ها نیز دارای توزیع کوشی استاندارد است. یعنی داریم $$\bar{X}\sim Cauchy (0,1)$$.
• توزیع t با یک درجه آزادی همان توزیع کوشی استاندارد است. یعنی اگر $$X\sim t(1)$$ آنگاه $$X\sim Cauchy (0,1)$$ خواهد بود.
• اگر $$X\sim Cauchy (\theta , y)$$ آنگاه kX+l نیز دارای توزیع کوشی با پارامترهای $$\theta k +l$$ و $$\gamma|k|$$ است. یعنی داریم $$X\sim Cauchy(\theta k +l, \gamma|k|)$$ است.
• اگر $$X\sim Cauchy (\theta_1,\gamma_1)$$ و $$Y\sim Cauchy(\theta_2,\gamma_2)$$ باشند، آنگاه به شرط مستقل بودن X و Y داریم:

$$\large X+Y\sim Cauchy(\theta_1+\theta_2,\gamma_1+\gamma_2)$$

و همچنین برای تفاضل دو متغیر تصادفی کوشی مستقل می‌توان نوشت:

$$\large X-Y\sim Cauchy(\theta_1-\theta_2,\gamma_1+\gamma_2)$$

• برای متغیر تصادفی X با توزیع کوشی با پارامترهای مکان $$\theta=0$$ و $$\gamma$$ دلخواه داریم: $$\frac{1}{X}\sim Cauchy (0,\frac{1}{\gamma})$$
• اگر X یک متغیر تصادفی با توزیع یکنواخت استاندارد باشد، آنگاه تانژانت $$\pi(X-\frac{1}{2})$$ دارای توزیع کوشی استاندارد است. یعنی می‌توان نوشت:

$$\large \displaystyle X\sim {\textrm {U}}(0,1) \rightarrow \tan \left(\pi \left(X-{\tfrac {1}{2}}\right)\right)\sim {\textrm {Cauchy}}(0,1)$$

کاربرد توزیع کوشی

یکی از کاربردهای جالب برای توزیع کوشی، مسئله فانوس دریایی است. این مسئله اولین بار توسط استفن گال (Stephen Gull) در سال 1988 مطرح شد. صورت مسئله در ادامه آمده است.

فرض کنید یک فانوس دریایی به فاصله $$\beta$$ از ساحل قرار دارد. طول جغرافیایی این فانوس برابر با $$\alpha$$ است. به این معنی که روی ساحل نیز نقطه‌ای با مختصات مثلا ($$\alpha,0$$) متناظر با فانوس‌دریایی وجود دارد. فانوس دریایی به طور تصادفی ولی با توزیع یکنواخت چشمک می‌زند. در نتیجه زاویه تابش آن نیز تصادفی است.

اشعه نورانی حاصل از این چشمک‌ها، به ساحل برخورد و بوسیله حسگرهای نور، شناسایی می‌شود. ولی متاسفانه این حسگرها، زاویه نور را شناسایی نمی‌کنند، بلکه فقط مشخص می‌کنند که آیا نور به آن‌ها تابیده شده یا خیر. با استفاده از حسگرهایی که در موقعیت‌ طول‌های جغرافیایی مختلف نصب شده، N بار برخورد نور ثبت شده است. فانوس دریایی کجاست؟

با توجه به اینکه زاویه تابش تصادفی است، مسئله باید برمبنای احتمال حل شود. فرض کنید تابع احتمال برای زاویه تابش یکنواخت باشد. یعنی اگر $$\theta$$ زاویه تابش باشد داریم:

$$\large \theta \sim U(-\frac{\pi}{2},\frac{\pi}{2})$$

پس تابع احتمال برای آن به صورت زیر نوشته می‌شود:

$$\large f(\theta,\alpha,\beta)=\frac{1}{\pi}$$

خواهیم دید که توزیع متغیر تصادفی X کوشی با پارامترهای $$\alpha$$ و $$\beta$$ است که براساس داده‌های مشاهده شده می‌توان آن‌ها را برآورد و موقعیت فانوس دریایی را بدست آورد.

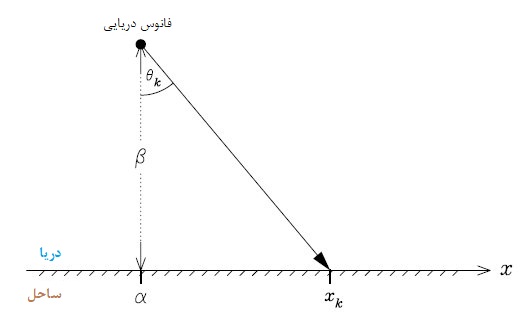
با استفاده از رابطه زیر می‌توان موقعیت x را برحسب دو پارامتر $$\alpha$$ و $$\beta$$ نوشت.

$$\large X=\beta \tan \theta +a$$

با استفاده از تغییر متغیر برای محاسبه تابع چگالی احتمال، می‌توان تابع چگالی احتمال X را برحسب زاویه یعنی $$\theta$$ بدست آورد. پس داریم:

$$\large f_X(x|\alpha,\beta)=f_{\theta}(\theta| \alpha,\beta)\mid\frac{d\theta}{dx}\mid$$

در نتیجه با استفاده از مشتق‌گیری می‌توان نوشت:

$$\large \dfrac{d\theta}{dx}=\beta \sec^2(\theta)=\dfrac{\beta}{(x-\alpha)^2+\beta^2}$$

بر این اساس تابع چگالی احتمال برای متغیر تصادفی X به صورت زیر حاصل می‌شود.

$$\large f_X(x|\alpha,\beta)=\frac{1}{\pi}\dfrac{\beta}{(x-\alpha)^2+\beta^2}$$

که همان توزیع کوشی با پارامترهای $$\alpha$$ و $$\beta$$ است. بنابراین براساس تابع درستنمایی و بیشینه‌سازی آن می‌توان پارامترهای این توزیع را به کمک داده‌های جمع‌آوری شده از همه حسگرها برآورد کرد و مختصات فانوس دریایی را بدست آورد.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آزمایش تصادفی، پیشامد و تابع احتمال
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های نرم‌افزارهای آماری
• توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها
• توزیع های آماری F و T — مفاهیم و کاربردها
• توزیع های آماری گاما و بتا — مفاهیم و کاربردها

^^