درس الگوریتم های پیشرفته | مفاهیم پایه به زبان ساده

درس الگوریتم های پیشرفته از جمله مفاد درسی مقطع کارشناسی ارشد رشتههای مهندسی کامپیوتر - نرمافزار، مهندسی کامپیوتر - الگوریتمها و محاسبات و مهندسی کامپیوتر- هوش مصنوعی است. همچنین، درس الگوریتم های پیشرفته یکی از دروس اختیاری مقطع کارشناسی ارشد رشته مهندس فناوری اطلاعات نیز محسوب میشود. علاوه بر آنکه درس الگوریتم های پیشرفته یکی از مباحث درسی رشتههای مهندسی کامپیوتر و فناوری اطلاعات است، یک مبحث پایهای برای فعالیت در حوزههای «هوش مصنوعی» (Artificial Intelligence)، «یادگیری ماشین» (Machine Learning) و «علم داده» (Data Science) نیز به شمار میآید. تسلط بر مبحث تحلیل و طراحی الگوریتم ها و نظریه الگوریتم های پیشرفته به برنامهنویسها نیز در حل بهتر مسائل برنامهنویسی و نوشتن کدهایی با کارایی و سرعت اجرای بالاتر و مصرف حافظه کمتر، کمک شایان توجهی میکند.
درس الگوریتم های پیشرفته در مقطع کارشناسی ارشد، در واقع ادامه درس تحلیل و طراحی الگوریتم ها است که در دوران کارشناسی به دانشجویان مقطع کارشناسی مهندسی کامپیوتر و مهندسی فناوری اطلاعات تدریس میشود. برای مقطع کارشناسی در دانشگاههای پیامنور، از کتاب فارسی منتشر شده توسط انتشارات همین دانشگاه و به کوشش احمد فراهی، سید ناصر آیت و جعفر تنها استفاده میشود. در دانشگاههای دولتی روزانه و شبانه، دانشگاه های غیر انتفاعی و دانشگاههای آزاد اسلامی، بر اساس نظر هیئت علمی و اساتید دانشگاه، تدریس از روی یکی از کتب مرجع به زبان انگلیسی، منابع فارسی و یا جزوههای تالیفی اساتید انجام میشود. در مقطع کارشناسی ارشد، مراکز آموزشی و پژوهشی مختلف، معمولا برای درس الگوریتم های پیشرفته از منابع انگلیسیزبان و یا جزوههای تالیفی اساتید استفاده میکنند.
با وجود این تنوع در استفاده از منابع، سرفصلهای مورد استفاده اساتید هم در مقطع کارشناسی و هم در مقطع کارشناسی ارشد برای درس تحلیل و طراحی الگوریتم ها و درس الگوریتم های پیشرفته مشابه است. البته، معمولا در برخی از دانشگاهها، در مقطع کارشناسی ارشد نیز برخی از مباحث درس تحلیل و طراحی الگوریتم ها به عنوان مقدمه یا پیشنیازی بر درس الگوریتم های پیشرفته تدریس میشود. همچنین، فعالان حوزه فناوری اطلاعات، هوش مصنوعی، یادگیری ماشین، علم داده، برنامهنویسی و دیگر حوزههایی که علاقهمند به یادگیری تحلیل، طراحی و نوشتن الگوریتم ها و درس الگوریتم های پیشرفته هستند، معمولا نیاز به شروع از مباحث اولیه تا رسیدن به موارد پیشرفتهتر دارند. در این مطلب، کلیه سرفصلهایی که برای درس تحلیل و طراحی الگوریتم ها و درس الگوریتم های پیشرفته بیان میشود، مورد بررسی قرار گرفتهاند.
الگوریتم چیست؟
در درس تحلیل و طراحی الگوریتم ها، ابتدا به مفهوم الگوریتمها پرداخته میشود. بنابراین، در اینجا نیز ابتدا واژهشناسی کلمه «الگوریتم» (Algorithm)، تعریف الگوریتم، مثالی از یک الگوریتم، کاربردهای الگوریتمها و آینده الگوریتمها مورد بررسی قرار میگیرد. کلمه الگوریتم بر خلاف تصویر بسیاری از افراد که فکر میکنند این کلمه از ریشه کلمههای یونانی Arithmos (به یونانی αριθμός) به معنای «عدد» و «Algos» (به یونانی άλγος) به معنای «درد» است، از این دو کلمه گرفته نشده است.
بلکه، این کلمه از نام دانشمند ایرانی قرن نهم میلادی، «محمد بن موسی خوارزمی» (Muhammad ibn Musa al-Khwarizmi) گرفته شده است. خوارزمی، بیشتر به خاطر نوشتن رساله «المختصر في حساب الجبر والمقابلة» (The Compendious Book on Calculation by Completion and Balancing) معروف است؛ کتابی که کلمه «جبر» (Algebra) از آن آمده است. خوارزمی در رساله دیگری نیز سیستم دهدهی نوین را برای نوشتن و دستکاری اعداد معرفی کرد.
«الگوریتم» (Algorithm) یک توالی صریح، دقیق، بدون ابهام و قابل اجرا به لحاظ مکانیکی از دستورات اولیه است که معمولا برای انجام کار و هدف خاصی، تعبیه شدهاند. در واقع، یک الگوریتم روال یا فرمولی برای حل یک مسئله بر مبنای انجام یک توالی از فعالیتها است. یک برنامه کامپیوتری را میتوان یک الگوریتم حاوی جزئیات دقیق در نظر گرفت. الگوریتمها به طور گسترده در حوزه فناوری اطلاعات مورد استفاده قرار میگیرند.
به بیانی دیگر، میتوان گفت که الگوریتم یک مجموعه از عملیات مرتب و محدود است که باید به منظور حل مسئله خاصی دنبال میشوند. این یعنی یک زنجیره از دستورالعملهای دقیق وجود دارند که باید به ترتیب خاصی دنبال شوند. هدف الگوریتم حل یک مسئله است و این یعنی الگوریتمها دارای هدف از پیش تعریف شده هستند. در واقع، هدف از نوشتن یک الگوریتم، تولید یک خروجی است.
اگر الگوریتمها برای مسائل جهان واقعی نوشته شوند، باید ضمن نوشتن آنها، کلیه حالاتی که ممکن است هنگام اجرای الگوریتم با آن مواجه شود، در نظر گرفته شوند. به همین دلیل است که الگوریتمهایی که برای مسائل دنیای واقعی نوشته میشوند، پیچیده، بزرگ و همچون درختی از دستورالعملها هستند. الگوریتم و مفهوم آن، نه فقط در درس تحلیل و طراحی الگوریتم ها که پایه و اساس درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته است.
در درس تحلیل و طراحی الگوریتم، به مباحث مقدماتیتر و برخی از انواع روشهای طراحی و ساخت الگوریتمها پرداخته شده است و در درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته روشهای پیچیدهتر ساخت الگوریتمها و مباحث پیشرفتهتر در این حوزه، مورد بررسی قرار گرفته است.
مثالی از یک الگوریتم
برنامهای بنویسید که مجموع دو عدد دلخواه را محاسبه کند. یک نمونه الگوریتم برای انجام این کار به صورت زیر است.
- گام ۱: شروع
- گام ۲: عدد دلخواه اول را دریافت کن.
- گام ۳: عدد دلخواه دوم را دریافت کن.
- گام ۴: مجموع دو عدد دریافت شده را محاسبه کن.
- گام ۵: حاصل جمع را اعلام کن.
- گام ۶. پایان.
الگوریتم لازم برای جمع دو عدد دلخواه را به صورت زیر نیز می توان نوشت.
- گام ۱: شروع.
- گام ۲: دو عدد دلخواه را دریافت کن.
- گام ۳: مجموع دو عدد دریافت شده را محاسبه کن.
- گام ۴: حاصل جمع را اعلام کن.
- گام ۵: پایان.
کاربردهای الگوریتمها و مسائلی که با الگوریتمها حل میشوند
اکنون که مفهوم الگوریتم بیان شد، جالب است که به این موضوع هم اشاره شود که همه افراد در زندگی روزمره خود، بی آنکه بدانند، روزانه از الگوریتمها برای انجام فعالیتهای روزمره خود استفاده میکنند. برای مثال، دم کردن چای یا پوشیدن لباس، هر یک الگوریتمهای خاص خود را دارند. اشخاص در مشاغل گوناگون نیز برای انجام کار روزانه خود از الگوریتمهای ذهنی یا مکتوب خاصی برای انجام کارها و انجام وظایف بهره میبرند. برنامهنویسها نیز مانند سایر افراد هستند.
اما با نگاهی جزئیتر و ویژهتر، باید گفت که هنگامی که یک برنامهنویس یک برنامه را میسازد، در واقع یک مجموعه از الگوریتمها را ساخته است. یک برنامه کامپیوتری، یک مجموعه از دستورهای داده شده به ماشین است که به زبان خاصی نوشته شدهاند تا یک مجموعه مشخص از فعالیتها را برای کسب نتیجه مشخص و از پیش تعریف شدهای انجام دهند. البته از آنجا که ماشینها در حال حاضر زبان انسان را به طور مستقیم متوجه نمیشوند، برنامهنویسها از زبانهای برنامهنویسی برای تعامل با آنها استفاده میکنند.

آینده الگوریتمها و نقش آنها در محاسبات
پیش از آنکه کامپیوترها وجود داشته باشند، الگوریتمها وجود داشتند. اما امروزه و پس از ابداع کامپیوترها، الگوریتمهای بیشتری نیز ایجاد شدند. الگوریتمها در قلب محاسبات قرار دارند. الگوریتمها در ابتدا به طور جدی برای حل مسائل «مرتبسازی» (Sorting) توسعه داده شدند، ولی امروزه در پروژههای عظیم از پروژه ژنوم انسان گرفته تا وبسایتهایی که همه روزه با حجم انبوهی از دادهها سر و کار دارند، همه و همه از الگوریتمها استفاده شده است. برخی از پژوهشگران بر این باور هستند که آینده از آن الگوریتمها است. زیرا در حقیقت، این الگوریتمها هستند که در قلب فناوریهای بسیار قدرتمندی مانند «هوش مصنوعی» (Artificial Intelligence) و «علم داده» (Data Science) قرار دارند.
الگوریتمها در حال حاضر مبنای فناوریهای یادگیری خودکار یا «یادگیری ماشین» (Machine Learning) هستند. در پس فناوریهایی مانند «دستیار مجازی» (ٰVirtual Assistants) و «اتومبیلهای خودران» نیز الگوریتمها قرار دارند. این صرفا بخشی از جایگاه فعلی الگوریتمها است و در آینده این جایگاه تغییرات قابل توجهی خواهد داشت و به همین دلیل است که برخی پژوهشگران معتقد هستند آینده در دستان الگوریتمها است. به همین دلیل است که مطالعه درس تحلیل و طراحی الگوریتم ها و درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته نه فقط به دانشجویان رشتههای مرتبط، بلکه به کلیه برنامهنویسان، کارشناسان علم داده، هوش مصنوعی و دیگر زمینههای فناوری اطلاعات توصیه میشود.
فلوچارت
«فلوچارت» (Flowchart) نوعی نمودار است که جریان کاری یا فرایند را نشان میدهد. میتوان گفت که یک فلوچارت در واقع نمایش نموداری یک الگوریتم و یک رویکرد مرحله به مرحله برای حل مسئله است. فلوچارت از اشکال هندسی تشکیل شده است که هر یک نماد نوع خاصی از عملیات هستند. این فلوچارتها با استفاده از جهتنماها به یکدیگر متصل شدهاند. این نمایش بصری در واقع مدل راهکار برای یک مسئله داده شده را نشان میدهد.
از فلوچارتها برای تحلیل، طراحی، مستندسازی یا مدیریت یک فرایند یا برنامه در زمینههای مختلف استفاده میشود. اهمیت فلوچارتها در بحث تحلیل و طراحی الگوریتمها نیز به دلیل موارد بیان شده و البته، نمایش الگوریتمها با استفاده از فلوچارتها در بسیاری از مواقع است. مبحث فلوچارتها در درس تحلیل و طراحی الگوریتم ها مورد بررسی قرار میگیرد و انتظار میرود فرد پیش از مطالعه درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته بر مبحث فلوچارتها تسلط داشته باشد.
ساختارهای داده
«ساختار داده» (Data Structure) راهکاری برای ذخیرهسازی و سازماندهی دادهها به منظور تسهیل دسترسی و ویرایش آنها است. هیچ ساختار دادهای یکتایی وجود ندارد که برای همه مسائل و اهداف خوب باشد و بنابراین، نیاز به شناخت انواع ساختار دادهها و نقاط ضعف و قوت آنها است. در این بخش، انواع ساختارهای داده (مقدماتی) که در درس تحلیل و طراحی الگوریتمها نیز وجود دارند و به طور کلی در ابتدای مسیر به آنها نیاز است، معرفی میشوند. ساختارهای داده پیشرفته نیز که مربوط به درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته هستند و به طور کلی متخصصان برای وظایف پیشرفتهتری به آنها نیاز دارند، در بخش بعدی معرفی شدهاند.
مجموعهها همانقدر برای علوم کامپیوتر اساسی محسوب میشوند که برای ریاضیات مبنا و اساس هستند. با وجود آنکه در ریاضیات مجموعهها غیر قابل تغییر هستند، اما مجموعههایی که توسط الگوریتمها دستکاری میشوند، میتوانند بزرگ یا کوچک شوند یا در گذر زمان، دستخوش تغییراتی شوند. به چنین مجموعههایی، «مجموعه پویا» (Dynamic Set) گفته میشود. در ادامه، روشهای پایهای برای نمایش و دستکاری مجموعههای پویای متناهی در کامپیوترها، معرفی شدهاند.
آرایه
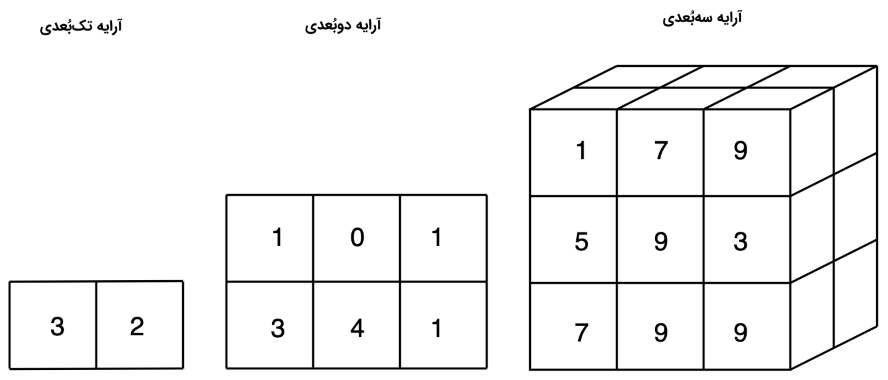
در علوم کامپیوتر، «ساختار داده آرایه» (Array Data Stucture) یا «آرایه» (Array) ساختار دادهای است که شامل عناصری (مقادیر یا متغیرها) میشود که هر یک حداقل با یک اندیس یا کلید آرایه مشخص شدهاند. آرایه به گونهای ذخیره میشود که جایگاه هر یک از عناصر آن را میتوان بر اساس «تاپل» (Tuple) اندیسها با استفاده از یک فرمول ریاضی محاسبه کرد. سادهترین نوع ساختار دادهها یک آرایه خطی است که به آن آرایه یکبُعدی نیز گفته میشود. ساختار داده آرایه جزو پایهایترین ساختارهای داده محسوب میشود و انتظار میرود که فرد پیش از مطالعه درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته به آن تسلط داشته باشد.
صف
«صف» (Queue) یک مجموعه داده پویا است که در آن، عناصر با عملیات «حذف» (Delete) پاک میشوند و با عملیات «درج» (Insert) وارد میشوند. در صف، عنصری که حذف میشود عنصری است که زودتر (اول) به صف وارد شده است و در واقع، صف به صورت «اول ورود-اول خروج» (First-In, First-Out که به اختصار به آن FIFO گفته میشود) یا خروج به ترتیب ورود پیادهسازی میشود. مثال سادهای از صف که در دنیای روزمره وجود دارد، صف نانوایی است که در آن، اولین فردی که برای دریافت نان در صف قرار میگیرد، اولین نفری نیز هست که سرویس خواهد گرفت و نان دریافت میکند.
صف انواع گوناگونی دارد که عبارتند از صف خطی، صف حلقوی و صف اولویتدار. صف اولویتدار یکی از پرکاربردترین انواع صف است. ساختار داده صف نیز مانند آرایه جزو پایهایترین ساختارهای داده محسوب میشود و انتظار میرود که فرد پیش از مطالعه درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته به آن تسلط داشته باشد.

صف اولویتدار
در علوم کامپیوتر، «صف اولویتدار» (Priority Queue) یک نوع داده انتزاعی شبیه به صف یا پشته معمولی است که در آن، هر عنصر دارای یک «اولویت» (Priority) تخصیص داده شده به آن نیز هست. در صف اولویتدار، یک عنصر با اولویت بالا، پیش از عنصری با اولویت کم خدمات دریافت میکند.
در برخی از پیادهسازیها، اگر دو عنصر اولویت یکسانی داشته باشند، مطابق با ترتیبی که در آن در صف قرار گرفتهاند خدمات دریافت میکنند، هر چند در اغلب پیادهسازیهای صف اولویتدار، داشتن عناصری با اولویت یکسان امری تعریف نشده است. ساختار داده صف اولویتدار در درس تحلیل و طراحی الگوریتم ها تشریح میشود و فرد پیش از مطالعه درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته باید به آن تسلط داشته باشد.
پشته
«پشته» (Stack) یک مجموعه داده پویا است که در آن، عناصر با عملیات «حذف» (Delete) پاک میشوند و با عملیات «درج» (Insert) وارد میشوند. در پشته، عنصری که حذف میشود، عنصری است که دیرتر (آخر) وارد شده است و در واقع، پشته به صورت «آخر ورود-اول خروج» (Last-In, First-Out که به اختصار به آن LIFO گفته میشود) است. مثال سادهای از پشته که در دنیای روزمره وجود دارد، چیدن بشقابها روی هم داخل کابینت است. آخرین بشقابی که چیده میشود (بشقابی که روی همه بشقابها قرار دارد) اولین بشقابی است که برداشته میشود. ساختار داده پشته در درس تحلیل و طراحی الگوریتم ها تشریح میشود و فرد پیش از مطالعه درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته باید به آن تسلط داشته باشد.

لیستهای پیوندی
«لیست پیوندی» (Linked List) یک ساختار داده است که در آن، اشیا برخلاف «آرایه» (Array)، به ترتیب خطی سازماندهی شدهاند. در آرایه ترتیب خطی با اندیس آرایه مشخص میشوند؛ حال آنکه در لیست پیوندی، با اشارهگرها به هر شی معلوم میشود. لیست پیوندی یک ارائه ساده و منعطف برای مجموعههای پویا را فراهم و از عملیات گوناگون لیستها، پشتیبانی میکند. لیست پیوندی انواع مختلفی دارد که لیست پیوندی یک طرفه، دو طرفه و حلقوی از جمله آنها هستند. ساختار لیست پیوندی در درس تحلیل و طراحی الگوریتم ها تشریح میشود و فرد پیش از مطالعه درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته باید به آن تسلط داشته باشد.

درختهای ریشهدار
«درخت ریشهدار» (Rooted Tree) درختی است که در آن، یک رأس «ریشه» (Root) تعیین شده است. یالهای یک درخت ریشهدار میتواند به طور طبیعی از سمت ریشه و یا به سمت ریشه باشد. درختهای ریشهدار معمولا همراه با یک یک ساختار افزوده مانند مرتبسازی همسایهها در هر رأس، یک ساختار داده کلیدی در علوم کامپیوتر محسوب میشوند.
درختها یکی از پرکاربردترین انواع ساختارهای داده هستند که برخی از انواع مقدماتیتر آن که در این بخش معرفی شدهاند در درس تحلیل و طراحی الگوریتم ها و انواع پیشرفتهتر آن که در بخش بعدی معرفی شدهاند، در درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته مورد بررسی قرار میگیرند.
درخت جستجوی دودویی
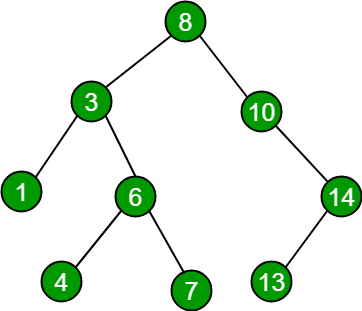
«درخت جستجوی دودویی» (Binary Search Tree)، از بسیاری از عملیات مجموعه دادههای پویا شامل جستجو (Search)، بیشینه (Maximum)، کمینه (Minimum)، ماقبل (Predecessor)، مابعد (Successor)، درج (Insert) و حذف (Delete) پشتیبانی میکند. بنابراین میتوان از یک درخت دودویی هم به عنوان «دیکشنری» (Dictionary) و هم به عنوان صف اولویت استفاده کرد. درخت دودویی همانطور که از نام آن مشخص است، به شیوهای سازماندهی شده است که هر راس میتواند حداکثر دو رأس داشته باشد.
یک درخت را می توان با ساختار داده پیوندی نمایش داد که در آن، هر گره یک شی است. درخت جستجوی دودویی در درس تحلیل و طراحی الگوریتم ها و انواع پیشرفتهتر آن که در بخش بعدی معرفی شدهاند، در درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته مورد بررسی قرار میگیرند.
درخت قرمز-مشکی
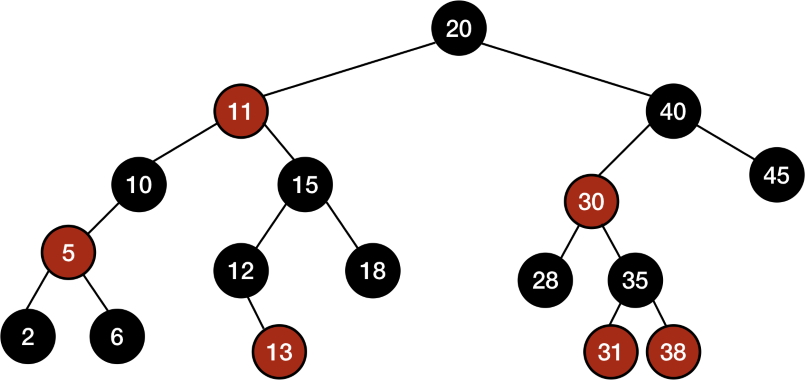
«درخت قرمز-مشکی» (Red-Black Tree) یک درخت جستجوی دودویی با یک بیت فضای اضافی به ازای هر گره است. این یک بیت اضافی، رنگ گره است که میتواند قرمز یا مشکی باشد. درخت قرمز-مشکی با محدود کردن رنگ گره در هر مسیر ساده از ریشه به برگها، اطمینان حاصل میکند که هیچ مسیری بیش از دو برابر از مسیر دیگر، بلندتر نیست و بنابراین، تقریبا «متوازن» (Balanced) است. درخت قرمز-مشکی از جمله ساختار دادههای درخت مقدماتی است. اما در برخی مواقع، این نوع ساختار داده به جای درس تحلیل و طراحی الگوریتم ها در درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته مورد بررسی قرار میگیرد.
جدول هش
در بسیاری از کاربردها، نیاز به یک مجموعه پویا است که از عملیات درج (Insert)، جستجو (Search) و حذف (Delete) (عملیات دیکشنری یا Dictionary Operation) پشتیبانی کند. برای مثال، کامپایلری که یک زبان برنامهنویسی را ترجمه میکند، یک جدول نمادها را نگهداری میکند که در آن کلیدهای عناصر رشته کاراکترهای دلخواه متناظر با شناساگرها در آن زبان برنامهنویسی هستند. «جدول هش» (Hash Table) یک ساختار داده موثر برای پیادهسازی دیکشنریها است.
جستجوی یک عنصر در جدول هش میتوانند به اندازه جستجوی عنصر در لیست پیوندی به طول بیانجامد. جدول هش به عنوان یک ساختار داده پایهای و مهم، گاه در درس تحلیل و طراحی الگوریتم ها و گاهی در درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته مورد بررسی قرار میگیرد.
ساختارهای داده تجمیعی
در برخی مسائل، استفاده از ساختار دادههایی که پیش از این بیان شد برای حل مسئله کفایت میکنند. اما در بسیاری از دیگر مسائل نیاز به خلاقیت بیشتری است. البته، معمولا در مسائل نادری نیاز به آن است که یک ساختار داده کاملا جدید ساخته شود. در اغلب موارد، تجمیع ساختار دادههایی که در بالا بیان شد برای حل مسائل کافی است. دو ساختار داده شناخته شدهای که با تجمیع کردن ساخته شدهاند، در ادامه آمدهاند. برخی از انواع ساختار دادههای تجمیعی در درس تحلیل و طراحی الگوریتم ها و برخی از دیگر انواع آن، در درس درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته مورد بررسی قرار میگیرند.
- آمارهای با ترتیب پویا (Dynamic Order Statistics)
- درختهای فاصلهای (Interval Trees)
ساختارهای داده پیشرفته
در این بخش، ساختار دادههایی مورد بررسی قرار میگیرند که از عملیات پیشرفتهتری روی مجموعه دادههای پویا پشتیبانی میکنند. البته ساختار دادههایی که در ادامه معرفی میشوند تنها ساختار دادههای پیشرفته موجود نیستند و ساختار دادههای پیشرفته دیگری مانند «درخت پویا» (Dynamic Tree)، «درخت گسترده» (Splay Tree)، «ساختار داده ماندگار» (Persistent Data Structure)، «درخت تلفیقی» (Fusion Tree)، «گراف پویا» (Dynamic Graph) و بسیاری از دیگر انواع ساختار دادههای پویا وجود دارند.
ساختار دادههایی که در ادامه معرفی شدهاند، در درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته مورد بررسی قرار میگیرند.
درختهای بی
«درختهای بی» (B-Trees) درختهای جستجوی متوازنی هستند که برای کار روی دیسکها یا دیگر دستگاههای ذخیرهسازی ثانویه دارای دسترسی مستقیم استفاده میشوند. درختهای بی شباهت زیادی به درختهای قرمز-مشکی دارند، با این تفاوت که درختهای بی عملکرد بهتری را در کاهش عملیات ورودی/خروجی (I/O) دارند.
بسیاری از سیستمهای پایگاه داده از درختهای بی یا گونههایی از درخت بی برای ذخیرهسازی اطلاعات استفاده میکند. تفاوت درخت بی با درخت قرمز-مشکی در آن است که گرههای درخت بی ممکن است تعداد زیادی فرزند داشته باشند، این تعداد از چند عدد تا چند هزار فرزند متفاوت است.
هرم فیبوناچی
ساختار داده «هرم فیبوناچی» (Fibonacci Heap) به دو هدف خدماتدهی میکند؛ اول آنکه از یک مجموعه از عملیات که چیزی با عنوان «هرم ادغام شونده» (Mergeable Heap) را تشکیل میدهند پشتیبانی میکند و دوم آنکه چندین عملیات هرم فیبوناچی در زمان استهلاکی ثابتی اجرا میشوند که موجب میشود این ساختار داده به خوبی برای کاربردهایی که مکررا به این عملیات ارجاع پیدا میکنند، مفید باشد.
درخت ون امد بوآس
در هر یک از ساختار دادههای صف اولویت دار، درخت قرمز-مشکی و هرم فیبوناچی، حداقل یک یک عملیات مهم چه در حالت استهلاکی و چه در بدترین حالت، از درجه زمانی (O (lg n است. «درخت ون امد بوآس» (Van Emde Boas Trees) با بهرهگیری از ساختار داده ویژه خود، در عین پشتیبانی از عملیاتی که سایر ساختاردادههای گفته شده از آنها پشتیبانی میکنند، این عملیات را در درجه زمانی کمتری انجام میدهد.
ساختار دادههای ویژه مجموعههای منفصل
برخی از عملیات شامل گروهبندی n عنصر متمایز در مجموعه با استفاده از «مجموعههای منفصل» (Disjoint Sets) انجام میشوند. این کاربردها معمولا به طور کلی نیاز به انجام دو عملیات دارند که عبارت هستند از پیدا کردن مجموعه یکتایی که حاوی یک عنصر داده شده است و متحد کردن دو مجموعه. در بحث «ساختار دادههای ویژه مجموعههای منفصل» (Data Structures for Disjoint Sets) راهکارهایی برای نگهداری ساختار دادههایی که عملیات بیان شده پشتیبانی کنند، مورد بررسی قرار میگیرد.
تحلیل الگوریتمها
«تحلیل الگوریتم» (Analyzing Algorithm) به معنای پیشبینی منابعی است که الگوریتم به آن نیاز دارد. گاه به گاهی، منابعی مانند حافظه، پهنای باند ارتباطی یا سختافزار کامپیوتری، نگرانی اصلی هستند؛ اما در اغلب موارد، زمان محاسبات (زمان انجام محاسبات توسط الگوریتم) است که نیاز به اندازهگیری آن است. اساسا با تحلیل چندین الگوریتم پیشنهادی برای یک مسئله، میتوان کارآمدترین الگوریتم برای یک مسئله خاص را پیدا کرد. چنین تحلیلهایی ممکن است بیش از یک کاندیدای مناسب را معرفی کنند، اما معمولا میتوان چندین مورد از بدترین موارد را کنار گذاشت.
پیش از آنکه بتوان یک الگوریتم را تحلیل کرد، باید مدلی از فناوری پیادهسازی آن داشت که شامل مدلی برای منابع آن فناوری و هزینههای آنها میشود. در برخی از منابع شامل کتاب «مقدمهای بر الگوریتمها» (Introduction to algorithms)، یک مدل «ماشین دسترسی تصادفی» (Random Access Machine | RAM) تک پردازندهای برای محاسبات به عنوان فناور پیادهسازی در نظر گرفته میشود و همچنین، بنا بر این است که الگوریتم به عنوان یک برنامه کامپیوتری پیادهسازی خواهد شد.
درجه رشد و نماد O بزرگ
در تحلیل الگوریتمها معمولا «بدترین حالت» (Worst Case)، «حالت متوسط» (Average Case) و «بهترین حالت» (Best Case) محاسبه و نتایج آن با یکدیگر و دیگر الگوریتمها مقایسه میشوند تا نتیجهگیری شود که کدام الگوریتم برای یک مسئله خاص کارآمدتر است. منظور از بدترین حالت زمان اجرا، طولانیترین زمان برای اجرای یک عملیات است. «درجه رشد» (Rate of Growth) یا «مرتبه رشد» (Order of Growth) یک الگوریتم راهکاری برای گفتن/پیشبینی زمان اجرای یک برنامه و فضا/حافظه اشغال شده توسط آن است. درجه رشد در واقع یک مشخصه کلی از کارآمدی الگوریتم ارائه و البته، به کارشناس این امکان را میدهد که کارآمدی نسبی الگوریتمهای جایگزین را بسنجد.
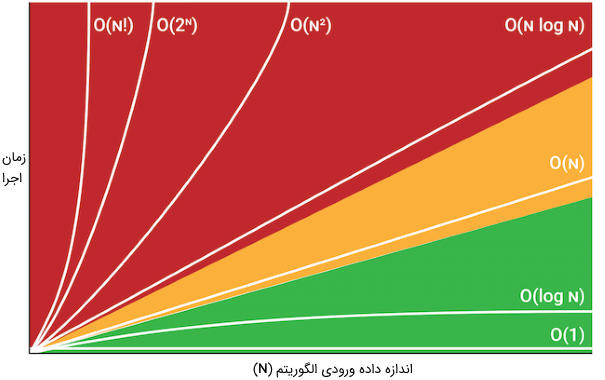
محبوبترین و متداولترین گزینه برای بیان درجه رشد، «نماد O بزرگ» (Big O Notation) است. این علامت در واقع بدترین حالت زمان اجرا برای یک الگوریتم را بیان میکند. برای مثال وقتی گفته میشود یک الگوریتم از درجه (O (n است، یعنی در بدترین حالت، برای به دست آوردن پاسخ باید n عملیات انجام دهد. نماد O بزرگ عضوی از خانواده نمادهای ابداع شده توسط «پائول گوستاو هاینریش باخمان» (Paul Gustav Heinrich Bachmann)، «ادموند لانداو» (Edmund Landau) و دیگران است که به این خانواده از نمادها «نمادهای باخمان-لانداو» (Bachmann–Landau Notation) یا «نماد تقریبی» (Asymptotic Notation) گفته میشود.
تحلیل پیشرفته الگوریتمها و آنالیز استهلاکی
در «تحلیل استهلاکی» (Amortized Analysis) که به آن «آنالیز استهلاکی» نیز گفته میشود، میانگین زمان مورد نیاز برای انجام یک توالی از عملیات ساختار داده برای کل عملیات انجام شده، محاسبه میشود. با بهرهگیری از تحلیل استهلاکی، میتوان نشان داد که اگر میانگین برای یک توالی از عملیات گرفته شود، میانگین هزینه یک عملیات کوچک است؛ حتی اگر یک عمل از عملیات در توالی بسیار پرهزینه باشد.
آنالیز استهلاکی یا همان تحلیل استهلاکی، از جمله مباحثی است که در درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته به طور کامل و جمع مورد بررسی قرار میگیرد.
ردهبندی مسائل محاسباتی
تقریبا همه الگوریتمهایی که در درس تحلیل و طراحی الگوریتم ها و درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته مورد بررسی قرار میگیرند، «الگوریتمهایی با درجه زمانی چند جملهای» (Polynomial-Time Algorithms) هستند. یعنی، برای یک ورودی با اندازه n، بدترین زمان اجرای آنها از مرتبه (O (nk است که در آن k یک عدد ثابت است.
پرسشی که ممکن است پیش بیاید این است که آیا همه الگوریتمها از درجه زمانی چند جملهای هستند؟ پاسخ منفی است. مسائلی (مانند مسئله توقف آلن تورینگ که یکی از مسائل مشهور است) وجود دارند که صرفنظر از مدت زمانی که برای اجرای آنها وجود دارد، توسط هیچ کامپیوتری قابل حل نیستند. در بحث ردهبندی مسائل محاسباتی به این موضوع پرداخته میشود. در ادامه، انواع ردههای مسائل محاسباتی موجود بیان شدهاند.
- مسائل پی (P-Problem): این مسائل جزو مسائل یک کلاس پیچیدگی پایهای در حوزه نظریه پیچیدگی محاسباتی محسوب میشوند که امکان حل آنها با «ماشین تورینگ قطعی» (Deterministic Turing Machine) در در زمان چند جملهای وجود دارد.
- مسائل انپی (NP-Problem): این عنوان مخفف عبارت «Nondeterministic Polynomial Time» (زمان چند جملهای غیر قطعی) است. این کلاس از مسائل به مسائلی اشاره دارد که پاسخ آنها در زمان چند جملهای قابل به دست آوردن است. بررسی دقیقتر تفاوت مسائل P و NP از حوصله این مطلب خارج است و تنها اشاره به این نکته ضروری است که از دیرباز بحثهایی پیرامون تفاوتهای این دو رده از مسائل یا یکدیگر، وجود دارد.
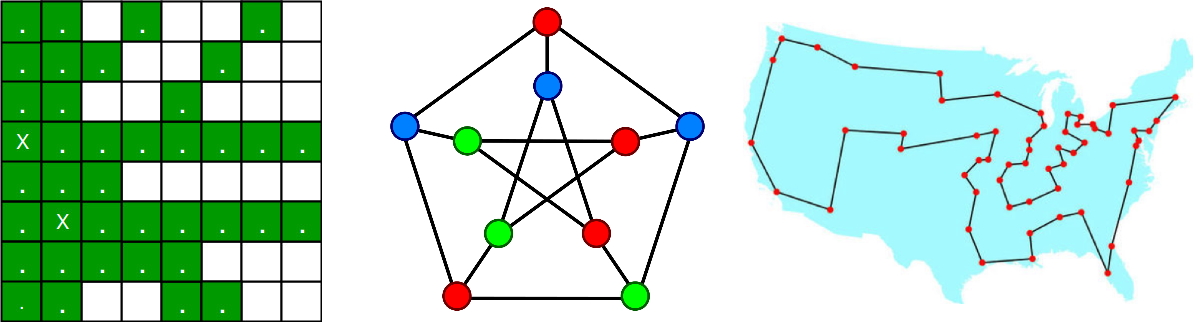
- مسائل انپی سخت (NP-Hard Problem): مسائل NP سخت (NP-Hardness) کلاسی از مسائل هستند که حداقل سختی آنها از حداکثر سختی مسائل NP بیشتر است. به عنوان یک مثال ساده از مسائل NP سخت میتوان به «مسئله جمع زیر مجموعهها» (Subset Sum Problem) اشاره کرد. از جمله مسائل NP Hard یا NP سخت معروف، «مسئله فروشنده دورهگرد» (Traveling Salesman Problem) است.
- مسائل انپی کامل (NP-Complete Problem): مسائل NP کامل (NP-Complete) به وسیله کلاس محدودی از «الگوریتمهای جستجوی جامع» (Brute-Force) قابل حل هستند. «مسئله رنگآمیزی گراف» (Graph Coloring Problem) یک مسئله NP Complete یا NP کامل است.
- مسائل قویا انپی-کامل (قویا انپی-سخت | Strongly NP-Complete Problem): «قویا انپی کامل» (Strong NP-Completeness) خصوصیتی از مسائل محاسباتی و نوعی خاصی از مسائل NP کامل است. یک مسئله را قویا NP کامل میگویند اگر حتی در صورتی که همه پارامترهای عددی آن از جهت طول ورودی به یک چند جملهای محدود شدند، باز هم NP کامل بماند.
الگوریتمهای مرتبسازی
- در علوم کامپیوتر، یک «الگوریتم مرتبسازی» (Sorting Algorithm) در واقع الگوریتمی است که عناصر یک لیست را به ترتیب خاصی قرار میدهد و اصطلاحا، مرتب میکند. متداولترین انواع مرتبسازی، «مرتبسازی عددی» (Numerical Order) و «مرتبسازی الفبایی» (Lexicographical Order) هستند. در بحث مرتبسازی، بهینهسازی کارایی الگوریتمهای مورد استفاده برای قرار دادن دادهها در یک لیست مرتب شده، (شامل الگوریتم جستجو و الگوریتم ادغام) بسیار حائز اهمیت است. از مرتبسازی برای «کانونیسازی» (Canonicalization) دادهها به منظور ساخت خروجیهای قابل درک برای انسان استفاده میشود. الگوریتمهای مرتبسازی باید دو شرطی که در ادامه آمده است را ارضا کنند.
- خروجی به ترتیب غیرکاهشی است (هر عنصر مطابق با ترتیب کامل مورد نظر، کوچکتر از عنصر پیش از خود نیست).
- خروجی یک «جایگشت» (Permutation) از ورودیها است (یک سازماندهی مجدد از ورودیها در عین حفظ همه عناصر اصلی).
الگوریتمهای مرتبسازی در سه دسته روشهای «مرتبسازی مقایسهای» (Comparison Sorts)، «مرتبسازی غیر مقایسهای» (Non-Comparison Sorts) و سایر روشها تقسیم میشوند. برخی از شناختهشدهترین و محبوبترین الگوریتمهای مرتبسازی برای هر یک از دستههای بیان شده، در ادامه آمدهاند. شایان توجه است که بخش عمده روشهای مرتبسازی در درس تحلیل و طراحی الگوریتم ها و برخی از آنها، در درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته مورد بررسی قرار میگیرند.
روشهای مرتبسازی مقایسهای
در این روشها همانطور که از نام آن نیز مشخص است، از مقایسه بین عناصر برای مرتبسازی استفاده میشود.
- مرتبسازی سریع (Quick Sort)
- مرتبسازی ادغامی (Merge Sort)
- مرتبسازی ادغامی درجا (In-Place Merge Sort)
- مرتبسازی درونگرا (Intro Sort)
- مرتبسازی هرمی (Heap Sort)
- مرتبسازی درجی (Insertion Sort)
- مرتبسازی بلوکی (Block Sort) یا مرتبسازی ادغام بلوک ( Block Merge Sort)
- مرتبسازی چهارگانه (Quad Sort)
- مرتبسازی تیم (Tim Sort)
- مرتبسازی انتخابی (Selection Sort)
- مرتبسازی مکعبی (Cube Sort)
- مرتبسازی شِل (Shell Sort)
- مرتبسازی حبابی (Bubble Sort)
- مرتبسازی درختی (Tree Sort)
- مرتبسازی دایرهای (Cycle Sort)
- مرتبسازی کتابخانهای (Library Sort)
- مرتبسازی شکیبانه (Patience Sorting)
- مرتبسازی روان (Smooth Sorting)
- مرتبسازی مسابقهای (Tournament Sort)
- مرتبسازی کوکتلی (Cocktail Shaker Sort)
- مرتبسازی شانهای (Comb Sort)
- مرتبسازی گورزاد (Gnome Sort)
- مرتبسازی زوج و فرد (Odd–Even Sort)
روشهای مرتبسازی غیرمقایسهای
در این روشهای مرتبسازی، از مقایسه عناصر برای مرتبسازی استفاده نمیشود.
- مرتبسازی لانه کبوتری (Pigeon Hole Sort)
- مرتبسازی سطلی (Bucket Sort)
- مرتبسازی شمارشی (Counting sort)
- مرتبسازی پایهای (Radix Sort) یا مرتبسازی مبنایی
- مرتبسازی گسترش یافته (Spread Sort)
- مرتبسازی انفجاری (Burst Sort)
- مرتبسازی فلش (Flash Sort)
سایر روشهای مرتبسازی
برخی از روشهای مرتبسازی نسبت به روشهای دیگری که پیشتر بیان شدند، کندتر هستند. از این الگوریتمها بیشتر برای مقاصد آموزشی استفاده میشود.
- مرتبسازی مهرهای (Bead Sort)
- مرتبسازی کلوچهای (Pancake Sorting)
- مرتبسازی اسپاگتی (Spaghetti Sort)
- شبکه مرتبسازی (Sorting Network)
- مرتبساز بایتونیک (Bitonic Merge Sort | Bitonic Sorter)
- مرتبسازی ساختگی (Bogo Sort)
- مرتبسازی دستنشانده (Stooge Sort)
روشهای طراحی الگوریتمها
با وجود آنکه افراد معمولا در صدد یادگیری الگوریتمهای آماده هستند، باید به این موضوع نیز توجه داشت که گاهی ممکن است با مسائلی مواجه شوند که نتوان یک الگوریتم آماده و از پیش تهیه شده برای آن پیدا کرد. این مسائل امروزه به طور خاص در حوزههای هوش مصنوعی و علم داده وجود دارند.
«روشهای» (Techniques) تحلیل و طراحی الگوریتمها به متخصصان کمک میکند تا الگوریتمهای اختصاصی خودشان را توسعه دهند، از اینکه آن الگوریتمها پاسخ صحیح را برای یک مسئله مییابند اطمینان حاصل کنند و همچنین، کارایی آن الگوریتمها را نیز بسنجند. در ادامه مطلب درس الگوریتم های پیشرفته برخی از این روشهای طراحی الگوریتمها مورد بررسی قرار میگیرند.
روشهای تکرار شونده
«روش تکرار شونده» (Iterative Method)، روش یا الگوریتمی است که گامهایی را با استفاده از یک یا چند حلقه، تکرار میکند. الگوریتمهایی که بر مبنای این روش ساخته میشوند، با تکرار یک یا چند گام، مسئله موجود را حل میکنند.
روشهای بازگشتی
در علوم کامپیوتری، «روش بازگشتی» (Recursive) روشی برای حل مسئله است که در آن، راهکار بسته به راهکارهایی برای نمونههای کوچکتر همان مسئله است. چنین مسائلی را میتوان به طور عمومی با روشهای تکرار شونده حل کرد، اما این کار نیازمند شناسایی و اندیسگذاری نمونههای کوچکتر در زمان برنامهنویسی است. بالعکس، بازگشت چنین مسائل بازگشتی را با استفاده از توابعی حل میکند که خودشان را از کد خودشان فراخوانی میکنند.
به بیان سادهتر، روش بازگشتی، روش یا الگوریتمی است که خودش را یک بار یا بیشتر با آرگومانهای مختلف فراخوانی میکند. در تعریف برنامهنویسی محورتری از «بازگشت» (Recursion) باید گفت که بازگشت فرایندی است که وقتی به وجود میآید که یک تابع یک کپی از خودش را روی مسئله کوچکتری فراخوانی میکند. هر تابعی که خودش را فراخوانی کند «تابع بازگشتی» (Recursive Function) است و چنین فراخوانی انجام شده توسط تابع، «فراخوانی بازگشتی» (Recursive Calls) نامیده میشود. شایان توجه است که روشهای بازگشتی قابل اعمال بر همه مسائل نیستند.
روشهای تقسیم و حل
در علوم کامپیوتر، «تقسیم و حل» (Divide and Conquer) یک پارادایم طراحی الگوریتم بر مبنای بازگشتهای چند شاخهای است. یک الگوریتم تقسیم و حل با شکستن بازگشتی یک مسئله به دو یا چند زیر مسئله از همان نوع یا انواع مرتبط تا هنگامی که این موارد به اندازهای ساده شوند که به طور مستقیم قابل حل باشند، کار میکند. الگوریتم تقسیم و حل مبنای الگوریتمهای کارآمدی برای مسائل گوناگون مانند مرتبسازی (مرتبسازی سریع، مرتبسازی ادغامی و دیگر موارد)، ضرب اعداد بزرگ (الگوریتم کاراتسوبا)، پیدا کردن نزدیکترین جفت نقاط، «تحلیل تجزیه کننده» (Syntactic Analysis) و «محاسبه تبدیل فوریه گسسته» (Discrete Fourier Transform | FFT) است.
روش شاخه و حد
روش «شاخه و حد» (Branch and Bound) که فارسی به آن انشعاب و تحدید و به اختصار به آن B&B ،BB یا BnB نیز گفته میشود، یک پارادایم طراحی الگوریتم برای مسائل «بهینهسازی گسسته» (Discrete Optimization)، «بهینهسازی ترکیبیاتی» (Combinatorial Optimization) و «بهینهسازی ریاضیاتی» (Mathematical Optimization) است. الگوریتم شاخه و حد (انشعاب و تحدید)، از شمارش منظم راهکارهای کاندید به وسیله جستجوی فضای حالت بهره میبرد. روشهای کاندید یک درخت ریشهدار را با یک مجموعه کامل به عنوان ریشه تشکیل میدهند. الگوریتم، شاخههای (انشعابهای) این درخت را اکتشاف میکند که نشانگر زیرمجموعهای از مجموعه راهکارها هستند.
روش حریصانه
«الگوریتم حریصانه» (Greedy Algorithm) به هر الگوریتمی گفته میشود که در آن، «اکتشاف حل مسئله» (Problem Solving Heuristics)، انجام انتخاب بهینه محلی با هدف رسیدن به بهینه سراسری را در هر گام دنبال کند. به زبان سادهتر، الگوریتمهای حریصانه در هر مرحله، از فرایند پیدا کردن پاسخ نهایی، بهترین پاسخ در همان مرحله را با در نظر داشتن هدف نهایی انتخاب میکنند. در بسیاری از مسائل، یک استراتژی حریصانه معمولا راهکار بهینه را تولید نمیکند، با این وجود، یک اکتشاف حریصانه ممکن است بهینه محلی را که تخمینی از راهکار بهینه سراسری است، در زمان قابل پذیرشی، به دست آورد.
برنامهنویسی خطی
«برنامهنویسی خطی» (Linear Programming | LP) که به آن «بهینهسازی خطی» (Linear Optimization) نیز گفته میشود، روشی برای به دست آوردن بهترین خروجی (مثلا بیشینه سود یا کمترین هزینه) در مدل ریاضی است که نیازمندیهای آن با روابط خطی نمایش داده میشود. به بیان رسمیتر، برنامهنویسی خطی روشی برای بهینهسازی یک تابع هدف خطی شامل معادله خطی و محدودیتهای نابرابری خطی است،
برنامهنویسی پویا
«برنامهنویسی پویا» (Dynamic Programming) هم یک روش بهینهسازی ریاضیاتی و هم یک روش برنامهنویسی کامپیوتری است. این روش توسط «ریچارد بلمن» (Richard Bellman) در سال ۱۹۵۰ توسعه پیدا کرد و کاربردهایی در حوزههای مختلف از مهندسی هوافضا گرفته تا اقتصاد دارد.
روشهای پَسگَرد
«پَسگَرد» (Backtracking) یک الگوریتم عمومی برای پیدا کردن همه (یا برخی) از راهکارها برای برخی از مسائل محاسباتی به ویژه «مسائل ارضای محدودیت» (Constraint Satisfaction Problems | CSP) است. این الگوریتم به طور افزایشی کاندیداهایی را برای راهکار میسازد و یک کاندیدا را به محض این تشخیص میدهد که آن کاندیدا احتمالا نمیتواند پاسخ مسئله باشد، فورا رها میکند (پسگرد). از جمله مسائلی که میتوان با روش پسگرد حل کرد، مسئله n وزیر است.
تحلیل احتمالی الگوریتمها
«تحلیل احتمالی» (Probabilistic Analysis) استفاده از احتمال در تحلیل مسائل است. معمولا، از تحلیل احتمالی برای تحلیل زمان اجرای الگوریتمها استفاده میشود. گاهی نیز از آن برای تحلیل دیگر کمیتها مانند هزینه استخدام در فرایند استخدام دستیار یا دیگر موارد استفاده میشود. به منظور انجام تحلیل احتمالی، باید از دانش پیرامون توزیع ورودیها و یا فرضیات درباره آن استفاده کرد. سپس، الگوریتم تحلیل و زمان اجرای میانگین محاسبه میشود که طی آن، میانگین زمان اجرا برای همه ورودیهای محتمل محاسبه میشود.
روشهای تصادفی
به منظور استفاده از تحلیل احتمالی، نیاز به دانستن چیزی پیرامون توزیع ورودیها است. در بسیاری از موارد اطلاعات کمی پیرامون توزیع ورودیها وجود دارد. حتی اگر اطلاعاتی پیرامون توزیع ورودیها نیز وجود باشد، ممکن است امکان مدل کردن این دانش به صورت محاسباتی نباشد. بنابراین، معمولا از احتمال و تصادفی بودن به عنوان ابزاری برای تحلیل و طراحی الگوریتم استفاده و بخشی از رفتار الگوریتم بهینه میشود. یک «الگوریتم تصادفی» (Randomized Algorithm) الگوریتمی است که درجهای از تصادفی بودن را به عنوان بخشی از منطق خود دارد.
چنین الگوریتمی معمولا از بیتهای دارای توزیع یکنواخت گسسته به عنوان یک ورودی کمکی برای هدایت رفتار آن به امید به دست آوردن کارایی خوب در حالت متوسط برای همه بیتهای ورودی تصادفی استفاده میکند. این دسته از روشها در درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته مورد بررسی قرار میگیرند.
روشهای چند ریسمانی
طیف وسیعی از الگوریتمهایی که در درس تحلیل و طراحی الگوریتم ها و درس الگوریتم های پیشرفته مورد بررسی قرار میگیرند، از رده الگوریتمهایی هستند که به آنها «الگوریتمهای ترتیبی» (Sequential Algorithm) یا «الگوریتمهای سریالی» (Serial Algorithm) گفته میشود. این الگوریتمها برای اجرا روی کامپیوترهای تک پردازندهای که در آنها در هر بار تنها یک دستور اجرا میشود مناسب هستند.
دسته دیگری از الگوریتمها، الگوریتمهای موازی (Parallel Algorithms) هستند که روی کامپیوترهای چندپردازندهای که امکان اجرای هم زمان چند دستور را میدهند اجرا میشوند. به طور کلی، متخصصان باید مدلهای خوبی از الگوریتمهای چند ریسمانی پویا را اکتشاف کنند که به همان میزان برای تحلیل و طراحی الگوریتمها پاسخگو هستند که در پیادهسازی عملی موثر واقع میشوند.

چند جملهای و تبدیل فوریه سریع
روش سرراست جمع زدن دو «چند جملهای» از درجه n دارای زمانی از درجه (O (n و روش سر راست ضرب کردن دو چند جملهای مذکور، زمانی از درجه (O (n2 است. «تبدیل فوریه سریع» (Fast Fourier Transform | FFT) یکی از الگوریتمهای مورد استفاده در «پردازش سیگنال» (Signal Processing) و آنالیز داده است که با استفاده از آن میتوان مدت زمان لازم برای انجام عملیات روی چندجملهایها را کاهش و مدت زمان ضرب آنها را به درجه (O (n log n میرساند.
روشهای نظریه اعداد
«نظریه اعداد» (Number-Theoretic Algorithms) در برههای از تاریخ علم، به عنوان مبحثی جذاب ولی بیکاربرد در ریاضیات محض محسوب میشد. امروزه، الگوریتمهای نظریه اعداد به طور گستردهای مورد استفاده قرار میگیرند.
از جمله این الگورتیمها میتوان به موارد زیر اشاره کرد.
- الگوریتمهای تجزیه به عاملهای عدد صحیح
- آزمون اول بودن ایکیاس (Agrawal-Kayal-Saxena)
- الگوریتم اقلیدس (Euclidean Algorithm)
- الگوریتم تعمیمیافته اقلیدس (Extended Euclidean Algorithm)
- الگوریتم جیسیدی دودویی (Binary GCD Algorithm)
- بهتوانرسانی پیمانهای (Modular Exponentiation)
- تولید اعداد اول (Generation of Primes)
روشهای تقریبی
بسیاری از مسائل حائز اهمیت عملی، NP-کامل (NP-Complete) و در عین حال، آنقدر با اهمیت هستند که نمیتوان آنها را بیپاسخ رها کرد. زیرا چگونگی پیدا کردن پاسخ بهینهای که در زمانی از درجه چند جملهای به دست بیاید، هنوز مشخص نیست. سه رویکرد کلی در برخورد با مسائل NP-کامل (NP-Complete) وجود دارد. اولین رویکرد، آن است که اگر ورودیهای واقعی بسیار کوچک باشند، الگوریتم با درجه نمایی هم ممکن است به طور رضایتبخشی کار کند. رویکرد دوم آن است که ممکن است بتوان برخی از شرایطهای مهم خاص را ایزوله و مسئله را بدین شکل در حالتی با درجه چند جملهای حل کرد. راهکار سوم، استفاده از «راهکارهای نزدیک به بهینه» (Near-Optimal Solutions) یا شبه بهینه است. روشهای تقریبی در درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته مورد بررسی قرار میگیرند.
الگوریتمهای گراف
مسائل گراف و الگوریتمهای گراف برای کار با آنها، در حوزه علوم کامپیوتر بسیار فراگیر هستند. «الگوریتمهای گراف» (Graph Algorithms) مسائل مرتبط با نظریه گراف را حل میکنند. به طور کلی، بسیاری از الگوریتمهای جذاب محاسباتی به گرافها مربوط هستند.
از جمله الگوریتمهای محبوب گراف، میتوان به موارد زیر اشاره کرد.
- الگوریتم *A
- الگوریتم دیکسترا (Dijkstra's Algorithm)
- جستجوی اول عمق (Depth-First Search)
- جستجوی اول سطح (Breadth-First Search)
- الگوریتم فلوید-وارشال (Floyd–Warshall Algorithm)
- الگوریتم فورد فالکرسون (Ford–Fulkerson Algorithm)
- الگوریتم بروکا (Borůvka's Algorithm)
- الگوریتم کروسکال (Kruskal's Algorithm)
- الگوریتم پریم (Prim's Algorithm)
- نزدیکترین همسایگی (Nearest Neighbour)
تطبیق رشته
در علوم کامپیوتر، «الگوریتمهای تطبیق رشته» (String-Matching Algorithms) که به آنها «الگوریتمهای جستجوی رشته» (String-Searching Algorithms) نیز گفته میشود، کلاس مهمی از الگوریتمهای رشته هستند که در تلاش برای پیدا کردن محل وقوع یک یا چند رشته در رشته یا متن طولانیتری هستند. از جمله الگوریتمهای معروف جستجوی رشته میتوان به موارد زیر اشاره کرد:
- الگوریتم ساده جستجوی رشته (Naive Pattern Searching Algorithm)
- الگوریتم رابین کارپ (Rabin-Karp Algorithm)
- الگوریتم بویر مور (Boyer–Moore String-Search Algorithm)
- الگوریتم تطبیق رشته آهو-کوراسیک (Aho–Corasick String Matching Algorithm)
هندسه محاسباتی
«هندسه محاسباتی» (Computational Geometry) شاخهای از علوم کامپیوتر است که در آن به مطالعه الگوریتمهای مربوط به حل مسائل هندسی پرداخته میشود. در مهندسی و ریاضیات مدرن، هندسه محاسباتی کاربردهای متعددی را در حوزهها گوناگون شامل گرافیک کامپیوتری، رباتیک، «یکپارچهسازی کلانمقیاس» (Very-Large-Scale Integration | VLSI)، «طراحی به کمک رایانه» (Computer-Aided Design)، «مدلسازی مولکولی» (Molecular modelling)، «متالورژی» (Metallurgy)، «تولید» (Manufacturing)، «طراحی پارچه» (Textile Layout)، «جنگلداری» (Forestry) و «آمار» (Statistics) کاربرد دارد.
ورودی یک مسئله هندسه محاسباتی، معمولا توصیفی از مجموعهای از اشیای هندسی مانند مجموعهای از نقاط، خطوط یا راسهای چند ضلعی در جهت حرکت عقربههای ساعت است. برخی از مسائل معروف هندسه محاسبتی، در ادامه امدهاند:
- پوش محدب (Convex Hull)
- دیاگرام ورونوی (Voronoi Diagram)
- برنامهنویسی خطی (Linear Programming)
- نزدیکترین جفت نقاط (Closest Pair of Points)
- کوتاهترین مسیر اقلیدسی (Euclidean Shortest Path)
- تولید مِش (Mesh Generation)
- نزدیکترین همسایگی (Nearest Neighbor)

کتب مرجع برای درس تحلیل و طراحی الگوریتم ها و درس الگوریتم های پیشرفته
در ادامه، تعدادی از کتب مرجع برای درس تحلیل و طراحی الگوریتم و درس الگوریتم های پیشرفته مورد بررسی قرار میگیرد. در برخی موارد، بخشهایی از کتب معرفی شده در مقطع کارشناسی و برای درس تحلیل و طراحی الگوریتم و بخشهایی از آنها در مقطع کارشناسی ارشد و برای درس الگوریتم های پیشرفته تدریس میشوند.
حال آنکه در مواردی نیز کتابی به عنوان منبع مقدماتی برای درس تحلیل و طراحی الگوریتم ها مورد استفاده قرار میگیرد و یک کتاب واحد نیز به عنوان مرجعی برای نظریه الگوریتم های پیشرفته برای تدریس درس نظریه الگوریتم پیشرفته یا همان درس الگوریتم های پیشرفته به کار میرود.
کتاب مقدمهای بر الگوریتم ها، ویرایش سوم
«کتاب مقدمهای بر الگوریتمها» (Introduction to Algorithms) که در این مطلب نیز به آن اشاره شد، به قلم «توماس اچ کورمِن» (Thomas H. Cormen)، «چارلز ای لایسرسان» (Charles E. Leiserson)، «رونالد ریوست» (Ronald L. Rivest) و «کلیفورد استین» (Clifford Stein) نوشته شده و با عنوان کتاب تحلیل و طراحی الگوریتم های CLRS (سرنام اسامی نویسندگان) یا کتاب کورمن مشهور است. این کتاب در بسیاری از دانشگاههای جهان و البته ایران به عنوان منبع و مرجع آموزش درس تحلیل و طراحی الگوریتم ها و درس الگوریتم های پیشرفته یا همان درس نظریه الگوریتم پیشرفته به کار میرود. این کتاب از جمله کتبی است که بخشهایی از آن در مقطع کارشناسی و با عنوان درس تحلیل و طراحی الگوریتمها و بخشهایی از آن برای درس نظریه الگوریتم پیشرفته یا درس الگوریتم های پیشرفته تدریس میشود.

- نویسنده(ها): توماس اچ کورمِن (Thomas H. Cormen)، چارلز ای لایسرسان (Charles E. Leiserson)، رونالد ریوست (Ronald L. Rivest) و کلیفورد استین (Clifford Stein)
- ناشر: انتشارات امآیتی (MIT Press)
- تعداد صفحات: 1292
- سال چاپ: ۳۱ جولای ۲۰۰۹ (۹ مرداد ۱۳۸۸)
کتاب مبانی الگوریتم ها با استفاده از شبه کد ++C، ویرایش سوم
«کتاب مبانی الگوریتمها با استفاده از شبهکد سیپلاسپلاس» (Foundations of Algorithms Using C++ Pseudocode) ارائه خوبی از بحث طراحی الگوریتمها، تحلیل پیچیدگی الگوریتمها و پیچیدگی محاسباتی را ارائه میکند. این کتاب نیز که با عنوان کتاب طراحی الگوریتم های نیپولیتان معروف است، به عنوان مرجعی برای درس تحلیل و طراحی الگوریتم ها و درس نظریه الگوریتم پیشرفته یا درس الگوریتم های پیشرفته استفاده میشود.

- نویسنده(ها): ریچارد نیپولیتان (Richard Neapolitan)
- ناشر: انتشارات جوج بارتلت (Jones And Bartlett Publishers)
- تعداد صفحات: 500
- سال چاپ: ۱۳ سپتامبر ۲۰۰۳ (۲۲ شهریور ۱۳۸۲)
سایر کتابهای مرجع برای درس تحلیل و طراحی الگوریتم ها و درس الگوریتم های پیشرفته
کتابهایی که معرفی شدند، بخشی از اصلیترین منابع این حوزه هستند و این در حالی است که کتابهای مرجع و محبوب دیگری نیز برای درس تحلیل و طراحی الگوریتم ها و درس الگوریتم های پیشرفته یا همان درس نظریه الگوریتم پیشرفته وجود دارد که در ادامه و به صورت کلی به آنها اشاره شده است.
- کتاب الگوریتمها، ویرایش چهارم (Algorithms, 4th Edition)
- نویسنده(ها): رابرت سجویک (Robert Sedgewick)
- ناشر: ادیسون-وزلی (Addison-Wesley Professional)
- تعداد صفحات: ۹۷۶
- سال چاپ: ۳ آوریل ۲۰۱۱ (۱۴ فروردین ۱۳۹۰)
- کتاب الگوریتمهای گروکینگ: یک راهنمای بصری برای برنامهنویسان و دیگر افراد علاقهمند (Grokking Algorithms: An illustrated guide for programmers and other curious people)
- نویسنده(ها): آدیتا بارگاوا (Aditya Bhargava)
- ناشر: منینگ (Manning)
- تعداد صفحات: ۲۵۶
- سال چاپ: ۱ می ۲۰۱۶ (۱۲ اردیبهشت ۱۳۹۵)
- کتاب قفلگشایی از الگوریتمها (Algorithms Unlocked)
- نویسنده(ها): توماس اچ کورمِن (Thomas H. Cormen)
- ناشر: انتشارات امآیتی (MIT Press)
- تعداد صفحات: ۲۴۰
- سال چاپ: ۱ مارس ۲۰۱۳ (۱۱ اسفند ۱۳۹۱)
- کتاب راهنمای طراحی الگوریتم، ویرایش دوم (The Algorithm Design Manual)
- نویسنده(ها): استیون اساس. اسکینا (Steven S S. Skiena)
- ناشر: اشپرینگر (Springer)
- تعداد صفحات: ۷۴۸
- سال چاپ: ۵ نوامبر ۲۰۱۰ (۱۴ آبان ۱۳۸۹)
- سادهسازی ساختارهای داده و الگوریتمها: ساختارهای داده و پازلهای الگوریتمی، ویرایش پنجم (Data Structures and Algorithms Made Easy: Data Structures and Algorithmic Puzzles, Fifth Edition)
- نویسنده(ها): ناراسیمها کارمانچی (Narasimha Karumanchi)
- ناشر: کریر مانک (CareerMonk Publications)
- تعداد صفحات: ۴۱۵
- سال چاپ: ۲۸ آگوست ۲۰۱۶ (۷ شهریور ۱۳۹۵)
منابع آموزشی ویدئویی برای درس تحلیل و طراحی الگوریتم ها و درس الگوریتم های پیشرفته
در ادامه، منابع آموزشی ویدئویی به زبان فارسی برای درس تحلیل و طراحی الگوریتمها و درس الگوریتم های پیشرفته یا همان درس نظریه الگوریتم پیشرفته معرفی شدهاند.

آموزش طراحی الگوریتم
این ویدئوی آموزشی توسط «مهندس فرشید شیرافکن» تدریس شده و طول مدت آن پانزده ساعت و دوازده دقیقه است. در این آموزش، مباحث مرتبه اجرایی، رابطههای بازگشتی و روش بازگشتی، روش تقسیم و حل، روش برنامهنویسی پویا، روش حریصانه، روش عقبگرد، روش شاخه و قید، الگوریتم های گراف و مسائل پی (مسائل P) و مسائل انپی (مسائل NP) مورد بررسی قرار گرفتهاند.
این دوره آموزش ویدئویی به طور خاص برای دانشجویان رشتههای مهندسی کامپیوتر و البته برای کلیه برنامهنویسان، فعالان حوزه هوش مصنوعی، علم داده و برخی از دیگر زمینهها مفید است.
آموزش طراحی الگوریتم به همراه حل مثال های عملی
این ویدئوی آموزشی توسط «مهندس مهدی اشرفی» تدریس شده و طول مدت آن هشت ساعت و شانزده دقیقه است. در این آموزش، ابتدا به آشنایی با طراحی الگوریتم پرداخته شده و سپس، مباحث روشهای بازگشتی، روشهای تقسیم و حل، روش حریصانه و روش برنامهنویسی پویا مورد بررسی قرار گرفتهاند.
آموزش طراحی الگوریتم (مرور – تست کنکور ارشد)
این ویدئوی آموزشی توسط «مهندس مهدی اشرفی» تدریس شده و طول مدت آن چهارده ساعت و چهل و هفت دقیقه است. رویکرد این آموزش مروری و با حل تستهای کنکور ارشد برای مباحث مرتبه اجرایی، روش بازگشتی، روش تقسیم و حل، روش پویا، روش حریصانه، روش عقبگرد، الگوریتمهای گراف و مسائل پی و انپی (مسائل P و مسائل NP) است.
آموزش مروری بر پیچیدگی محاسبات (Computational Complexity)
این ویدئوی آموزشی توسط «مهندس سحر اردلان» تدریس شده و طول مدت آن یک ساعت و سه دقیقه است. در این دوره آموزشی ضمن پرداختن به درآمدی بر نظریه محاسبات، مباحث محاسبهپذیری، محدودیتهای محاسبات الگوریتمی و محاسبهپذیری در زمان چند جملهای نیز مورد بررسی قرار گرفتهاند.
آموزش الگوریتم موازی و پردازش موازی
این ویدئوی آموزشی توسط «مهندس منوچهر بابایی» تدریس شده و طول مدت آن سیزده ساعت و دو دقیقه است. در این دوره، ضمن بیان مقدمهای پیرامون پردازش موازی و تحلیل الگوریتمها، مباحث مسئله انتخاب، ادغام، مرتبسازی، جستجو و عملیات ماتریسی مورد بررسی قرار میگیرند.
آموزش رابطههای بازگشتی در طراحی الگوریتم و ساختمان گسسته (مرور – تست کنکور ارشد)
این ویدئوی آموزشی توسط «مهندس فرشید شیرافکن» تدریس شده و طول مدت آن یک ساعت و پنجاه و چهار دقیقه است. رویکرد این آموزش مروری و با حل تستهای کنکور ارشد برای مبحث رابطههای بازگشتی است.
آموزش روش تقسیم و حل در طراحی الگوریتم (مرور – تست کنکور کارشناسی ارشد)
این ویدئوی آموزشی توسط «مهندس فرشید شیرافکن» تدریس شده و طول مدت آن یک ساعت و پنجاه دقیقه است. رویکرد این آموزش مروری و با حل تستهای کنکور ارشد برای مباحث روش تقسیم و حل است.
آموزش نرمافزار Raptor برای ترسیم فلوچارت
این ویدئوی آموزشی توسط «مهندس محمد جباری» تدریس شده و طول مدت آن پنجاه و سه دقیقه است. در این آموزشی چگونگی کار با نرمافزار Raptor و ترسیم فلوچارت با استفاده از آن مورد بررسی قرار گرفته است.
منابع آموزشی ساختمان داده ها
بحث ساختارهای داده و ساختمان داده ها از جمله مباحث مهمی است که در اغلب مراجع و دورههای آموزشی تحلیل و طراحی الگوریتم ها و درس الگوریتم های پیشرفته در ابعادی به آن پرداخته میشود.
هر چند که منابع جداگانه، مستق و جامعی برای این مبحث بسیار مهم وجود دارد. با توجه به ارتباط نزدیک مبحث ساختمان داده، تحلیل و طراحی الگوریتم ها و درس الگوریتم های پیشرفته، در ادامه تعدادی از منابع این حوزه نیز معرفی میشوند.
- آموزش ساختمان داده ها (مدرس: مهندس فرشید شیرافکن، طول مدت دوره: ده ساعت و بیست و هشت دقیقه)
- آموزش ساختمان داده ها همراه با پیاده سازی در ++C (مدرس: مهندس فرشید شیرافکن، طول مدت دوره: بیست و سه ساعت و شانزده دقیقه)
- آموزش ساختمان داده ها (مرور – تست کنکور ارشد) (مدرس: مهندس فرشید شیرافکن، طول مدت دوره: بیست ساعت و سی و پنج دقیقه)
- آموزش پیشرفته ساختمان داده (همراه با حل نمونه سوالات کنکور ارشد و دکتری) (مدرس: مهندس فرشید شرافکن، طول مدت دوره: هفت ساعت و پنجاه و هشت دقیقه)













مجموعههای پویا را فراهم مو از عملیات گوناگون لیستها، پشتیبانی میکند.
مو به و تبدیل بشه.
عکس درخت دودویی هم اصلاح بشه. درخت دودویی نیست و بیش از دو راس دارد
با سلام و احترام؛
صمیمانه از همراهی شما با مجله فرادرس و ارائه بازخورد سپاسگزاریم. اصلاحات لازم انجام شد.
برای شما آرزوی سلامتی و موفقیت داریم.
سلام خسته نباشید مقاله عالی ای بود.