«الگوریتم دایجسترا» (Dijkstra’s Algorithm) یا «اولین الگوریتم کوتاه‌ترین مسیر دایجسترا» (Dijkstra’s Shortest Path First Algorithm | SPF) (البته تلفظ صحیح این نام، الگوریتم دیکسترا است که به صورت متداول به آن دایجسترا گفته می‌شود)، الگوریتمی است که برای پیدا کردن کوتاه‌ترین مسیر بین دو «گره» (Node | راس) در گراف به کار می‌رود. این گراف، ممکن است نشان‌گر شبکه جاده‌ها یا موارد دیگری باشد. الگوریتم دایجسترا در سال ۱۹۵۶، توسط دانشمند کامپیوتری با نام «ادسخر ویبه دیکسترا» (Edsger Wybe Dijkstra) مطرح و سه سال بعد، منتشر شد. الگوریتم دایجسترا دارای انواع گوناگونی است. الگوریتم اصلی، کوتاه‌ترین مسیر بین دو گره را پیدا می‌کند؛ اما نوع متداول‌تر این الگوریتم، یک گره یکتا را به عنوان گره مبدا (آغازین) در نظر می‌گیرد و کوتاه‌ترین مسیر از مبدا به دیگر گره‌ها در گراف را با ساختن درخت کوتاه‌ترین مسیر پیدا می‌کند.
برای یک گره مبدا داده شده، الگوریتم، کوتاه‌ترین مسیر بین آن گره و دیگر گره‌ها را پیدا می‌کند. همچنین، الگوریتم دایجسترا برای پیدا کردن کوتاه‌ترین مسیر از یک گره یکتا به گره مقصد یکتای دیگری به کار می‌رود؛ برای انجام این کار، الگوریتم هنگامی که کوتاه‌ترین مسیر از مبدا به مقصد را پیدا کند، متوقف می‌شود. برای مثال، اگر گره‌های گراف نشان‌گر شهرها و یال‌ها هزینه سفر بین شهرهایی باشند که با جاده‌های مستقیم به هم متصل شده‌اند، از الگوریتم دایجسترا می‌توان برای پیدا کردن کوتاه‌ترین راه بین یک شهر و همه شهرهای دیگر استفاده کرد. یکی از کاربردهای اصلی الگوریتم دایجسترا، پروتکل‌های مسیریابی شبکه است که از جمله آن‌ها می‌توان به IS-IS (سیستم میانی به سیستم میانی | Intermediate System to Intermediate System) و «ابتدا کوتاه‌ترین مسیر باز» (Open Shortest Path First | OSPF) اشاره کرد.
از الگوریتم دایجسترا، به عنوان یک زیر روال نیز در برخی از دیگر الگوریتم‌ها مانند «الگوریتم جانسون» (Johnson’s Algorithm) استفاده می‌شود. الگوریتم دایجسترا از برچسب‌هایی استفاده می‌کند که اعداد صحیح یا حقیقی مثبت هستند. جالب توجه است که الگوریتم دایجسترا می‌تواند برای استفاده از برچسب‌های تعریف شده به هر شکلی، تعمیم پیدا کند. چنین تعمیمی، «تعمیم الگوریتم کوتاه‌ترین مسیر دایجسترا» نامیده می‌شود.
الگوریتم دایجسترا (Dijkstra) برای یافتن کوتاه‌ترین مسیر
فرض می‌شود که یک گراف به همراه یک راس مبدا داده شده و هدف پیدا کردن کوتاه‌ترین مسیر به همه راس‌های موجود در گراف مذکور است. الگوریتم دایجسترا شباهت زیادی به «الگوریتم پریم» (Prim’s Algorithm) برای «درخت پوشای کمینه» (Minimum Spanning Tree) دارد. در الگوریتم دایجسترا نیز درخت کوتاه‌ترین مسیر با استفاده از مبدا داده شده به عنوان ریشه، ساخته می‌شود. در هر مرحله از الگوریتم، راسی پیدا می‌شود که در مجموعه دیگر (مجموعه راس‌های در نظر گرفته نشده) قرار دارد و دارای کمترین فاصله از ریشه است. در ادامه، گام‌های مورد استفاده در الگوریتم دایجسترا به منظور یافتن کوتاه‌ترین مسیر از یک راس مبدا مجرد به دیگر راس‌ها در گراف داده شده به صورت مشروح بیان شده‌اند.
- ساخت مجموعه sptSet (مجموعه درخت کوتاه‌ترین مسیر | Shortest Path Tree Set) که به دنبال راس‌های قرار گرفته در درخت کوتاه‌ترین مسیر می‌گردد؛ یعنی، راسی که حداقل فاصله آن از مبدا محاسبه و نهایی شده است. به طور مقدماتی، این مجموعه خالی است.
- تخصیص یک مقدار فاصله به همه راس‌ها در گراف ورودی. مقداردهی اولیه همه مقادیر فاصله‌ها به عنوان INFINITE. تخصیص مقدار فاصله صفر به راس مبدا که موجب می‌شود این راس در ابتدا انتخاب شود.
- تا هنگامی که sptSet شامل همه راس‌ها نشده است، اقدامات زیر انجام می‌شود:
- راس u انتخاب می‌شود که در sptSet نیست و دارای حداقل مقدار فاصله است.
- u در sptSet قرار می‌گیرد.
- مقدار فاصله از همه راس‌های مجاور u به روز رسانی می‌شود. برای به روز رسانی مقادیر فاصله، در همه راس‌های مجاور تکرار انجام می‌شود. برای هر راس مجاور v، اگر مجموع فاصله u (از کد منبع) و وزن یال u-v کمتر از مقدار فاصله v باشد، مقدار فاصله از v به روز رسانی می‌شود.
برای درک بهتر موضوع، مثال زیر مورد بررسی قرار خواهد گرفت.
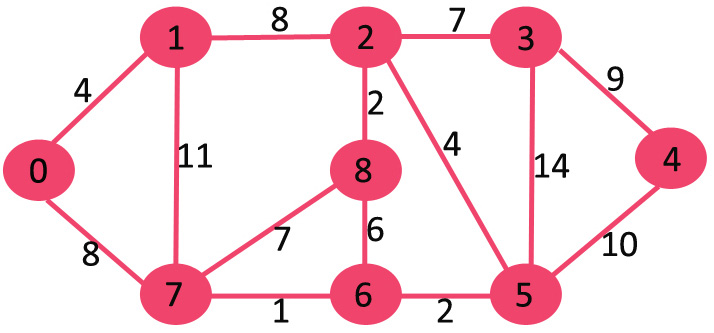
مجموعه sptSet در ابتدا خالی است و فاصله تخصیص پیدا کرده به راس‌ها برابر با { INF, INF, INF, INF, INF, INF, INF ,صفر} هستند که در آن INF نشان‌گر بی‌نهایت (Infinite) است. اکنون، باید راسی که دارای کمترین مقدار فاصله است انتخاب شود. راس ۰ انتخاب می‌شود و در sptSet قرار می‌گیرد. بنابراین، sptSet به صورت {0} می‌شود. پس از قرار دادن ۰ در sptSet، مقدار فاصله‌ها از راس‌های مجاور آن به روز رسانی می‌شوند. راس‌های مجاور ۰، راس‌های ۱ و ۷ هستند. مقدار فاصله برای ۱ و ۷، برابر با ۴ و ۸ است. زیرگراف زیر، راس‌ها و مقدار فاصله آن‌ها را نشان می‌دهد. در این گراف، تنها راس‌هایی با مقدار فاصله متناهی نشان داده شده‌اند. راس‌های موجود در SPT به رنگ سبز نمایش داده شده‌اند.
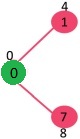
راسی که حداقل فاصله را از مبدا دارد و تاکنون انتخاب نشده است، یعنی در sptSET قرار ندارد، انتخاب می‌شود. راس ۱ انتخاب و به sptSet اضافه می‌شود. بنابراین، اکنون sptSet به صورت {۱ ,۰} خواهد بود. مقدار فاصله راس‌های مجاور ۱ به روز رسانی می‌شود. مقدار فاصله از راس ۲ برابر با ۱۲ خواهد بود.
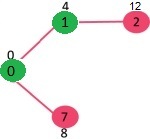
راسی با کمترین مقدار فاصله که در حال حاضر در SPT قرار ندارد باید انتخاب شود. راس ۷ انتخاب می‌شود. بنابراین، sptSet اکنون به صورت {۷ , 1 , ۰} خواهد بود. مقدار فاصله از راس‌های مجاور ۷ محاسبه می‌شود. مقدار فاصله از راس ۶ و ۸ متناهی است (به ترتیب، ۱۵ و ۹).
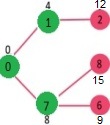
راسی با حداقل مقدار فاصله که در SPT نیز قرار ندارد باید انتخاب شود. راس ۶ انتخاب می‌شود. بنابراین، sptSet اکنون برابر با {۶ ,۷ ,۱ ,۰} است. مقدار فاصله‌ها از راس‌های مجاور ۶ باید به روز رسانی شود. مقدار فاصله برای راس‌های ۵ و ۸ به روز رسانی می‌شود.
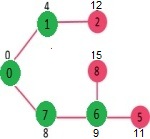
مراحل بیان شده تا جایی تکرار می‌شوند که sptSet شامل همه راس‌های گراف داده شده نباشد. در نهایت، درخت کوتاه‌ترین مسیر (SPT) زیر حاصل می‌شود.
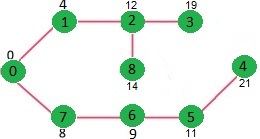
برای پیاده‌سازی الگوریتم بالا، از آرایه بولین []sptSet برای ارائه مجموعه‌ای از راس‌های قرار گرفته در SPT استفاده می‌شود. اگر مقدار [sptSet[v «درست» (True) باشد، راس v در SPT قرار می‌گیرد، در غیر این صورت، یعنی اگر [sptSet[v «غلط» (False) باشد، راس v در SPT قرار نمی‌گیرد. آرایه []dist برای ذخیره‌سازی کوتاه‌ترین مقدار فاصله از همه راس‌ها مورد استفاده قرار می‌گیرد.
کد الگوریتم دایجسترا در ++C
// A C++ program for Dijkstra's single source shortest path algorithm.
// The program is for adjacency matrix representation of the graph
#include <stdio.h>
#include <limits.h>
// Number of vertices in the graph
#define V 9
// A utility function to find the vertex with minimum distance value, from
// the set of vertices not yet included in shortest path tree
int minDistance(int dist[], bool sptSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (sptSet[v] == false && dist[v] <= min)
min = dist[v], min_index = v;
return min_index;
}
// A utility function to print the constructed distance array
int printSolution(int dist[], int n)
{
printf("Vertex Distance from Source\n");
for (int i = 0; i < V; i++)
printf("%d tt %d\n", i, dist[i]);
}
// Function that implements Dijkstra's single source shortest path algorithm
// for a graph represented using adjacency matrix representation
void dijkstra(int graph[V][V], int src)
{
int dist[V]; // The output array. dist[i] will hold the shortest
// distance from src to i
bool sptSet[V]; // sptSet[i] will be true if vertex i is included in shortest
// path tree or shortest distance from src to i is finalized
// Initialize all distances as INFINITE and stpSet[] as false
for (int i = 0; i < V; i++)
dist[i] = INT_MAX, sptSet[i] = false;
// Distance of source vertex from itself is always 0
dist[src] = 0;
// Find shortest path for all vertices
for (int count = 0; count < V-1; count++)
{
// Pick the minimum distance vertex from the set of vertices not
// yet processed. u is always equal to src in the first iteration.
int u = minDistance(dist, sptSet);
// Mark the picked vertex as processed
sptSet[u] = true;
// Update dist value of the adjacent vertices of the picked vertex.
for (int v = 0; v < V; v++)
// Update dist[v] only if is not in sptSet, there is an edge from
// u to v, and total weight of path from src to v through u is
// smaller than current value of dist[v]
if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX
&& dist[u]+graph[u][v] < dist[v])
dist[v] = dist[u] + graph[u][v];
}
// print the constructed distance array
printSolution(dist, V);
}
// driver program to test above function
int main()
{
/* Let us create the example graph discussed above */
int graph[V][V] = {{0, 4, 0, 0, 0, 0, 0, 8, 0},
{4, 0, 8, 0, 0, 0, 0, 11, 0},
{0, 8, 0, 7, 0, 4, 0, 0, 2},
{0, 0, 7, 0, 9, 14, 0, 0, 0},
{0, 0, 0, 9, 0, 10, 0, 0, 0},
{0, 0, 4, 14, 10, 0, 2, 0, 0},
{0, 0, 0, 0, 0, 2, 0, 1, 6},
{8, 11, 0, 0, 0, 0, 1, 0, 7},
{0, 0, 2, 0, 0, 0, 6, 7, 0}
};
dijkstra(graph, 0);
return 0;
}
کد الگوریتم دایجسترا در جاوا
// A Java program for Dijkstra's single source shortest path algorithm.
// The program is for adjacency matrix representation of the graph
import java.util.*;
import java.lang.*;
import java.io.*;
class ShortestPath
{
// A utility function to find the vertex with minimum distance value,
// from the set of vertices not yet included in shortest path tree
static final int V=9;
int minDistance(int dist[], Boolean sptSet[])
{
// Initialize min value
int min = Integer.MAX_VALUE, min_index=-1;
for (int v = 0; v < V; v++)
if (sptSet[v] == false && dist[v] <= min)
{
min = dist[v];
min_index = v;
}
return min_index;
}
// A utility function to print the constructed distance array
void printSolution(int dist[], int n)
{
System.out.println("Vertex Distance from Source");
for (int i = 0; i < V; i++)
System.out.println(i+" tt "+dist[i]);
}
// Funtion that implements Dijkstra's single source shortest path
// algorithm for a graph represented using adjacency matrix
// representation
void dijkstra(int graph[][], int src)
{
int dist[] = new int[V]; // The output array. dist[i] will hold
// the shortest distance from src to i
// sptSet[i] will true if vertex i is included in shortest
// path tree or shortest distance from src to i is finalized
Boolean sptSet[] = new Boolean[V];
// Initialize all distances as INFINITE and stpSet[] as false
for (int i = 0; i < V; i++)
{
dist[i] = Integer.MAX_VALUE;
sptSet[i] = false;
}
// Distance of source vertex from itself is always 0
dist[src] = 0;
// Find shortest path for all vertices
for (int count = 0; count < V-1; count++)
{
// Pick the minimum distance vertex from the set of vertices
// not yet processed. u is always equal to src in first
// iteration.
int u = minDistance(dist, sptSet);
// Mark the picked vertex as processed
sptSet[u] = true;
// Update dist value of the adjacent vertices of the
// picked vertex.
for (int v = 0; v < V; v++)
// Update dist[v] only if is not in sptSet, there is an
// edge from u to v, and total weight of path from src to
// v through u is smaller than current value of dist[v]
if (!sptSet[v] && graph[u][v]!=0 &&
dist[u] != Integer.MAX_VALUE &&
dist[u]+graph[u][v] < dist[v])
dist[v] = dist[u] + graph[u][v];
}
// print the constructed distance array
printSolution(dist, V);
}
// Driver method
public static void main (String[] args)
{
/* Let us create the example graph discussed above */
int graph[][] = new int[][]{{0, 4, 0, 0, 0, 0, 0, 8, 0},
{4, 0, 8, 0, 0, 0, 0, 11, 0},
{0, 8, 0, 7, 0, 4, 0, 0, 2},
{0, 0, 7, 0, 9, 14, 0, 0, 0},
{0, 0, 0, 9, 0, 10, 0, 0, 0},
{0, 0, 4, 14, 10, 0, 2, 0, 0},
{0, 0, 0, 0, 0, 2, 0, 1, 6},
{8, 11, 0, 0, 0, 0, 1, 0, 7},
{0, 0, 2, 0, 0, 0, 6, 7, 0}
};
ShortestPath t = new ShortestPath();
t.dijkstra(graph, 0);
}
}
//This code is contributed by Aakash Hasija
کد الگوریتم دایجسترا در #C
// A C# program for Dijkstra's single
// source shortest path algorithm.
// The program is for adjacency matrix
// representation of the graph
using System;
class GFG
{
// A utility function to find the
// vertex with minimum distance
// value, from the set of vertices
// not yet included in shortest
// path tree
static int V = 9;
int minDistance(int[] dist,
bool[] sptSet)
{
// Initialize min value
int min = int.MaxValue, min_index = -1;
for (int v = 0; v < V; v++)
if (sptSet[v] == false &&
dist[v] <= min)
{
min = dist[v];
min_index = v;
}
return min_index;
}
// A utility function to print
// the constructed distance array
void printSolution(int[] dist, int n)
{
Console.Write("Vertex Distance " +
"from Source\n");
for (int i = 0; i < V; i++)
Console.Write(i + " \t\t " +
dist[i] + "\n");
}
// Funtion that implements Dijkstra's
// single source shortest path algorithm
// for a graph represented using adjacency
// matrix representation
void dijkstra(int[,] graph, int src)
{
int[] dist = new int[V]; // The output array. dist[i]
// will hold the shortest
// distance from src to i
// sptSet[i] will true if vertex
// i is included in shortest path
// tree or shortest distance from
// src to i is finalized
bool[] sptSet = new bool[V];
// Initialize all distances as
// INFINITE and stpSet[] as false
for (int i = 0; i < V; i++)
{
dist[i] = int.MaxValue;
sptSet[i] = false;
}
// Distance of source vertex
// from itself is always 0
dist[src] = 0;
// Find shortest path for all vertices
for (int count = 0; count < V - 1; count++)
{
// Pick the minimum distance vertex
// from the set of vertices not yet
// processed. u is always equal to
// src in first iteration.
int u = minDistance(dist, sptSet);
// Mark the picked vertex as processed
sptSet[u] = true;
// Update dist value of the adjacent
// vertices of the picked vertex.
for (int v = 0; v < V; v++)
// Update dist[v] only if is not in
// sptSet, there is an edge from u
// to v, and total weight of path
// from src to v through u is smaller
// than current value of dist[v]
if (!sptSet[v] && graph[u, v] != 0 &&
dist[u] != int.MaxValue &&
dist[u] + graph[u, v] < dist[v])
dist[v] = dist[u] + graph[u, v];
}
// print the constructed distance array
printSolution(dist, V);
}
// Driver Code
public static void Main ()
{
/* Let us create the example
graph discussed above */
int[,] graph = new int[,]{{0, 4, 0, 0, 0, 0, 0, 8, 0},
{4, 0, 8, 0, 0, 0, 0, 11, 0},
{0, 8, 0, 7, 0, 4, 0, 0, 2},
{0, 0, 7, 0, 9, 14, 0, 0, 0},
{0, 0, 0, 9, 0, 10, 0, 0, 0},
{0, 0, 4, 14, 10, 0, 2, 0, 0},
{0, 0, 0, 0, 0, 2, 0, 1, 6},
{8, 11, 0, 0, 0, 0, 1, 0, 7},
{0, 0, 2, 0, 0, 0, 6, 7, 0}};
GFG t = new GFG();
t.dijkstra(graph, 0);
}
}
// This code is contributed by ChitraNayal
کد الگوریتم دایجسترا در پایتون
# Python program for Dijkstra's single
# source shortest path algorithm. The program is
# for adjacency matrix representation of the graph
# Library for INT_MAX
import sys
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
def printSolution(self, dist):
print "Vertex tDistance from Source"
for node in range(self.V):
print node,"t",dist[node]
# A utility function to find the vertex with
# minimum distance value, from the set of vertices
# not yet included in shortest path tree
def minDistance(self, dist, sptSet):
# Initilaize minimum distance for next node
min = sys.maxint
# Search not nearest vertex not in the
# shortest path tree
for v in range(self.V):
if dist[v] < min and sptSet[v] == False:
min = dist[v]
min_index = v
return min_index
# Funtion that implements Dijkstra's single source
# shortest path algorithm for a graph represented
# using adjacency matrix representation
def dijkstra(self, src):
dist = [sys.maxint] * self.V
dist[src] = 0
sptSet = [False] * self.V
for cout in range(self.V):
# Pick the minimum distance vertex from
# the set of vertices not yet processed.
# u is always equal to src in first iteration
u = self.minDistance(dist, sptSet)
# Put the minimum distance vertex in the
# shotest path tree
sptSet[u] = True
# Update dist value of the adjacent vertices
# of the picked vertex only if the current
# distance is greater than new distance and
# the vertex in not in the shotest path tree
for v in range(self.V):
if self.graph[u][v] > 0 and sptSet[v] == False and
dist[v] > dist[u] + self.graph[u][v]:
dist[v] = dist[u] + self.graph[u][v]
self.printSolution(dist)
# Driver program
g = Graph(9)
g.graph = [[0, 4, 0, 0, 0, 0, 0, 8, 0],
[4, 0, 8, 0, 0, 0, 0, 11, 0],
[0, 8, 0, 7, 0, 4, 0, 0, 2],
[0, 0, 7, 0, 9, 14, 0, 0, 0],
[0, 0, 0, 9, 0, 10, 0, 0, 0],
[0, 0, 4, 14, 10, 0, 2, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 1, 6],
[8, 11, 0, 0, 0, 0, 1, 0, 7],
[0, 0, 2, 0, 0, 0, 6, 7, 0]
];
g.dijkstra(0);
# This code is contributed by Divyanshu Mehta
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزشهای برنامهنویسی
- آموزش ساختمان داده‌ها
- مجموعه آموزشهای ساختمان داده و طراحی الگوریتم
- معرفی منابع آموزش ویدئویی هوش مصنوعی به زبان فارسی و انگلیسی
- زبان برنامهنویسی پایتون (Python) — از صفر تا صد
- آموزش ساختمان داده — مجموعه مقالات جامع وبلاگ فرادرس
^^
اگه بخوایم برنامه ها رو بنویسیم باید خط های نارنجی. و. قرمز و سبز هم بنویسیم؟
با سلام؛
از همراهی شما با مجله فرادرس سپاس‌گزاریم. آنچه در این کد به رنگ‌هایی به جز مشکی نمایش داده شده است، بخش‌های مختلف کد است که ویرایشگر کد متناسب با نوع آن بخش از کد، آن را به یکی از رنگ‌های بیان شده توسط شما درآورده است. برای مثال، توضیحات (کامنت‌ها)، توابع، شرط‌ها و دیگر موارد هر یک به رنگی درآمده‌اند. این کار توسط ویرایشگر کد به صورت خودکار و با این دلیل انجام می شود که خوانایی و عیب‌یابی کد افزایش پیدا کند. بنابراین، همه این موراد جزئی از یک کد کامل هستند. البته، توضحیات بخش غیر اجرایی و قابل حذف یک کد هستند که البته وجود آن‌ها برای افزایش خوانایی و به دلایل مهم دیگر، به نوعی الزامی است. برای مطالعه بیشتر پیرامون توضیحات، مطالعه مطلب زیر پیشنهاد می‌شود.
توضیحات در پایتون — به زبان ساده
پیروز، شاد و تندرست باشید.
سپاس
عالی
هر گونه بهرهگیری از مطالب مجله فرادرس به معنی پذیرش شرایط استفاده از آن بوده و کپی بخش یا کل هر کدام از مطالب، تنها با کسب مجوز مکتوب امکان پذیر است.
© فرادرس ۱۴۰۱
ورود / ثبت‌نام