تبدیل فوریه سریع (fft) — به زبان ساده

تبدیل فوریه سریع (Fast Fourier Transform) یا FFT یکی از مهم‌ترین الگوریتم‌های مورد استفاده در پردازش سیگنال و آنالیز داده است. در واقع FFT یک الگوریتم است که برای محاسبه تبدیل فوریه گسسته (Discrete Fourier Transform) یا DFT و نیز معکوس آن (IDFT) مورد استفاده قرار می‌گیرد. در این مطلب قصد داریم به بیان تبدیل فوریه سریع بپردازیم و روش‌های محاسبه آن را بررسی کنیم.

آنالیز فوریه می‌تواند یک سیگنال از حوزه اصلی، که معمولا زمان یا فضا است را به نمایشی در حوزه فرکانس و نیز بلعکس تبدیل کند. تبدیل فوریه گسسته معمولا از طریق تجزیه دنباله مقادیر، به عناصر با فرکانس‌های متفاوت محاسبه می‌شود. این تبدیل در بسیاری از رشته‌ها مفید است، اما مشکلی که وجود دارد این است که محاسبه مستقیم این تبدیل با استفاده از تعریف آن بسیار کند است و در عمل کاربردی ندارد. تبدیل فوریه سریع یا FFT روشی است که به وسیله آن می‌توان تبدیل فوریه گسسته را به سرعت محاسبه کرد. در واقع تبدیل فوریه سریع از طریق تجزیه ماتریس DFT به حاصلضرب ماتریس‌های تنک (Sparse) که در آن‌ها اکثر داریه‌های ماتریس صفر هستند، محاسبات را تسریع می‌بخشد.

در نتیجه، تبدیل فوریه سریع قادر است که پیچیدگی (Complexity) محاسبات DFT را از $$  \mathcal{O}[N^2] $$ به $$ \mathcal{O}[N\log N] $$ کاهش دهد. تبدیل فوریه گسسته مانند نوع آشناتر خود، یعنی تبدیل فوریه پیوسته، دارای فرم مستقیم و معکوس است.

کاربرد تبدیل فوریه

تبدیل فوریه سریع یا Fast Fourier Transform که به آن fft نیز می‌گویند، در علوم مهندسی می‌تواند برای تعیین فرکانس‌های غالب یک سیگنال ارتعاشی (Vibration Signal) به کار رود. زمانی که فرکانس‌های غالب (Dominant Frequencies) یک سیستم متناظر با فرکانس‌های طبیعی (Natural Frequency) آن باشند، ارتعاش‌های رخ داده می‌توانند به دلیل رزونانس (Resonance) تقویت شوند. این اتفاق می‌تواند تا حدی ادامه یابد که منجر به آسیب دیدن یا ریزش و تخریب یک سازه شود. فرض کنید یک سیستم صوتی در اختیار داریم و فرکانس طبیعی پنجره اتاق در حدود ۱۰۰ هرتز است. حال با استفاده از تبدیل فوریه می‌توانیم بدانیم که تا چه حد مجاز هستیم صدای صوت را بالا ببریم. در ادامه به بیان روشی برای پاسخ به این سوال و نیز سوالات مشابه می‌پردازیم.

سیگنال در حوزه زمان

تبدیل فوریه معمولا برای تبدیل یک سیگنال در طیف زمانی به سیگنالی در طیف فرکانسی مورد استفاده قرار می‌گیرد. مثال‌هایی از امواج در طیف زمانی را می‌توان سیگنال‌های صوتی، سیگنال‌های الکتریکی و ارتعاشات مکانیکی نام برد. تصویر زیر نمونه‌ای از یک سیگنال حوزه زمان را در طول ۰٫۲۵ ثانیه نشان می‌دهد.

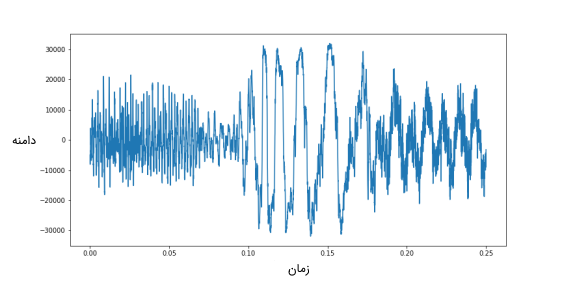
همان‌طور که از تصویر دیده می‌شود، این سیگنال شبیه به یک موج با فرکانس‌های مختلف و یا ترکیب چند موج است.

تبدیل فوریه گسسته

حال می‌خواهیم از تبدیل فوریه استفاده کنیم. تبدیل فوریه در واقع از این اصل استفاده می‌کند که هر تابع غیر خطی را می‌توان توسط مجموع بی‌نهایتِ امواج سینوسی نمایش داد. در تصویر زیر نمایی از مفهوم نمایش یک سیگنال توسط مجموع سیگنال‌های سینوسی نمایش داده شده است.

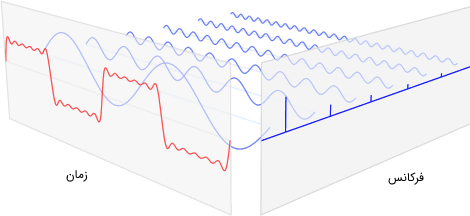
در واقع تصویر بالا نشان می‌دهد که یک تابع پله چگونه با استفاده از مجموع چندین موج سینوسی بازسازی می‌شود. نمودار قرمز رنگ نشان‌ دهنده تابع پله در حوزه زمان و نمودار آبی رنگ نشان‌ دهنده این تابع در حوزه فرکانس است. مجموع امواج سنوسی کوچک در پس زمینه تصویر می‌توانند تابع پله را بازسازی کنند.

تبدیل فوریه، یک سیگنال زمانی را تجزیه می‌کند و اطلاعاتی راجع به فرکانس‌های تمام امواج سینوسی مورد نیاز برای ساخت سیگنال حوزه زمان را در اختیار ما قرار می‌دهد.

برای یک دنباله با مقادیر فاصله برابر، فرمول تبدیل فوریه گسسته مستقیم به صورت زیر بیان می‌شود:

$$ X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-i~2\pi~k~n~/~N} $$

همچنین فرمول تبدیل فوریه گسسته معکوس به صورت زیر است:

$$ x_n = \frac{1}{N}\sum_{k=0}^{N-1} X_k e^{i~2\pi~k~n~/~N} $$

در فرمول بالا، $$ N $$ تعداد نمونه‌ها (Sample) و $$ n $$ نمونه فعلی است. همچنین $$ x_n $$ مقدار سیگنال در زمان n و $$ k $$ فرکانس فعلی (۰ هرتز تا N-1 هرتز) و $$ X_k $$ نتیجه حاصل از تبدیل فوریه گسسته است.

در واقع تبدیل از $$ x_n \to X_k $$، یک تبدیل از فضای پیکربندی به فضای فرکانس است. این تبدیل هم در بررسی طیف توان سیگنال و هم در انتقال برخی مسائل خاص به فضایی جهت انجام راحت‌تر محاسبات، بسیار مفید است.

برای سادگی ما فقط به تبدیل فوریه گسسته مستقیم می‌پردازیم؛ زیرا تبدیل فوریه گسسته معکوس را نیز می‌توان به صورت مشابه محاسبه کرد. با نگاهی دقیق‌تر به فرمول تبدیل فوریه گسسته در بالا، می‌توان به این نکته پی برد که این فرمول چیزی بیش از ضرب نقطه‌ای نیست.

همان طور که به یاد داریم، ضرب نقطه‌ای به صورت زیر ایجاد می‌شود:

$$ a \cdot b = \sum_{n=1}^{n}a_ib_i $$

بنابراین، فرمول بالا را می‌توان به این صورت بازنویسی کرد:

$$ \overrightarrow{X} = M \overrightarrow{x} $$

که در این فرمول ماتریس $$ M $$ به صورت زیر نوشته می‌شود:

$$ M_{kn} = e^{-i~2\pi~k~n~/~N}. $$

برای محاسبه ضرب نقطه‌ای در پایتون از کد زیر استفاده می‌شود:

import numpy as np

def DFT(x):
    """
    Compute the discrete Fourier Transform of the 1D array x
    :param x: (array)
    """

    N = x.size
    n = np.arange(N)
    k = n.reshape((N, 1))
    e = np.exp(-2j * np.pi * k * n / N)
    return np.dot(e, x)

اما باید به این نکته توجه کرد که اگر این برنامه را بر روی سیگنال حوزه زمان اجرا کنیم، که حدودا شامل ۱۰۰۰۰ نمونه است، آن‌گاه اجرای آن حدود ۱۰ ثانیه به طول می‌انجامد و با توجه به این‌که معمولا این دستور فقط بخشی از برنامه کلی مورد نیاز برای پروژه‌های مختلف است، می‌توان گفت سرعت بسیار پایینی دارد.

پیچیدگی محاسباتی تبدیل فوریه گسسته

همان طور که می‌دانیم، معادله تبدیل فوریه گسسته برای N نقطه از دنباله با طول محدود $$ x(n) $$ توسط فرمول زیر محاسبه می‌شود:

$$ X(k)=\sum\limits_{n=0}^{N-1}{x(n){{e}^{-j\tfrac{2\pi }{N}kn}}} $$

حال می‌خواهیم تعداد ضرب و جمع‌های مورد نیاز برای محاسبه تبدیل فوریه گسسته با استفاده از فرمول بالا را به دست آوریم. برای هر ضریب در تبدیل فوریه گسسته $$ X(k) $$، باید N عبارت را که شامل $$ x(1){{e}^{-j\tfrac{2\pi }{N}k \times 1}} $$، $$ x(0){{e}^{-j\tfrac{2\pi }{N}k \times 0}} $$ تا $$ x(N-1){{e}^{-j\tfrac{2\pi }{N}k \times (N-1)}} $$ هستند، محاسبه کنیم. سپس باید این عبارت‌ها را با هم جمع کنیم.

در حالت کلی $$ x(n) $$ یک عدد مختلط است و هر خروجی تبدیل فوریه گسسته تقریبا به N ضرب مختلط و N-1 جمع مختلط نیاز دارد. یک ضرب مختلط به تنهایی به ۴ ضرب حقیقی و ۲ جمع حقیقی نیاز دارد. به عنوان مثال، ضرب عدد مختلط $$ d_1=a_1+jb_1 $$ در $$ d_2=a_2+jb_2 $$، پاسخی برابر با $$ d_1d_2=(a_1a_2-b_1b_2)+j(b_1a_2+a_1b_2) $$ دارد.

علاوه بر این، یک جمع مختلط خود به ۲ جمع حقیقی نیاز دارد، بنابراین هر ضریب در تبدیل فوریه گسسته به $$ 4N $$ ضرب حقیقی و $$ 2N+2(N-1)=4N-2 $$ جمع حقیقی نیاز دارد. برای محاسبه تبدیل فوریه گسسته نهایی، لازم است تا معادله DFT را برای تمام N مقدار از k محاسبه کنیم. بنابراین آنالیز تبدیل فوریه N نقطه، به $$ 4N^2 $$ جمع حقیقی و $$ N(4N-2) $$ جمع حقیقی نیاز دارد. بنابراین، همان طور که قبلا نیز به آن اشاره کردیم، محاسبات مورد نیاز برای یک تبدیل فوریه گسسته N نقطه‌ای، از درجه $$ N^2 $$ خواهد بود. بنابراین با افزایش N، محاسبات مورد نیاز به سرعت افزایش می‌یابد. در شکل زیر، تعداد محاسبات ضرب حقیقی مورد نیاز بر حسب طول N تبدیل فوریه گسسته ترسیم شده است.

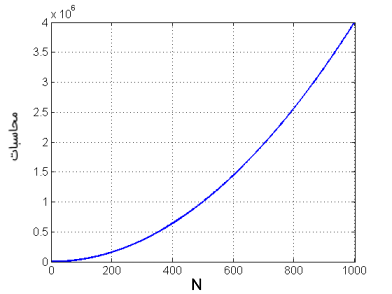
الگوریتم‌های زیادی برای بهبود مشکل تعداد بالای محاسبات و سرعت پایین در تبدیل فوریه گسسته به وجود آمده‌اند. در ادامه به بررسی یکی از این الگوریتم‌ها می‌پردازیم.

تبدیل فوریه سریع

افرادی به نام‌های کولی و توکی (Cooley and Tukey) توانستند الگوریتمی برای محاسبه تبدیل فوریه سریع یا Fast Fourier Transform به دست بیاورند. در این الگوریتم که مهم‌ترین الگوریتم تبدیل فوریه سریع است، به صورت بازگشتی (Recursively) تبدیل فوریه گسسته را به مسايل کوچک‌تر می‌شکند و زمان مورد نیاز برای انجام محاسبات را به مقدار قابل توجهی کاهش می‌دهد.

همان طور که قبلا هم اشاره شد، پیچیدگی یک مسئله تبدیل فوریه گسسته از درجه $$ \mathcal{O}[N^2] $$ به $$ \mathcal{O}[N\log N] $$ در تبدیل فوریه سریع کاهش می‌یابد. به این معنی که اگر $$ N= 10^6 $$ المان داشته باشد، انتظار می‌رود که یک الگوریتم FFT بتواند مسئله را در زمانی برابر با 50 ثانیه حل کند، اما این زمان برای تبدیل فوریه گسسته برابر با 20 ساعت خواهد بود. حال سوالی که پیش می‌آید این است که تبدیل فوریه سریع چگونه به این سرعت بالا در محاسبات دست می‌یابد؟

تقارن در تبدیل فوریه گسسته

یکی از مهم‌ترین ابزارها در ساخت یک الگوریتم در برنامه‌نویسی این است که تقارن را در حل مسئله اعمال کنیم. اگر به صورت تحلیلی بتوان نشان داد که یک قسمت از مسئله به قسمت دیگری از آن مشابه است، می‌توان به سادگی آن قسمت را یک بار محاسبه کرد و هزینه محاسباتی را کاهش داد. کولی و توکی نیز از همین روش استفاده کردند و حل مسئله تبدیل فوریه گسسته را سریع‌تر کردند.

حال می‌توان بیان روش را با این پرسش شروع کرد که مقدار $$ X_{N+k} $$ با توجه به فرمول تبدیل فوریه گسسته بالا چقدر است. پس از جایگذاری مقدار به صورت زیر به دست می‌آید:

$$ \begin{align*}
X_{N + k} &= \sum_{n=0}^{N-1} x_n \cdot e^{-i~2\pi~(N + k)~n~/~N}\\
&= \sum_{n=0}^{N-1} x_n \cdot e^{- i~2\pi~n} \cdot e^{-i~2\pi~k~n~/~N}\\
&= \sum_{n=0}^{N-1} x_n \cdot e^{-i~2\pi~k~n~/~N}
\end{align*} $$

در این فرمول از خاصیت همانندی (Identity) استفاده شده است که برای هر عدد صحیح n صحیح است.

خط آخر در فرمول بالا، مشخصه تقارن بسیار مهمی را در تبدیل فوریه گسسته نشان می‌دهد که در نتیجه آن داریم:

$$ X_{N+k} = X_k. $$

با بسط این عبارت به سادگی می‌توان نوشت که:

$$ X_{k + i \cdot N} = X_k $$

برای هر i صحیح، همان طور که در بالا نشان داده شد، این تقارن صادق است. بنابراین، تقارن را می‌توان برای محاسبه تبدیل فوریه گسسته با سرعت بالاتر نیز اعمال کرد.

اعمال تقارن و تبدیل DFT به FFT

کولی و توکی نشان دادند که این امکان وجود دارد که محاسبات لازم برای تبدیل فوریه گسسته را به دو قسمت کوچک‌تر بشکنیم. با استفاده از تعریف تبدیل فوریه گسسته داریم:

$$ \begin{align}
X_k &= \sum_{n=0}^{N-1} x_n \cdot e^{-i~2\pi~k~n~/~N} \\
&= \sum_{m=0}^{N/2 – 1} x_{2m} \cdot e^{-i~2\pi~k~(2m)~/~N} + \sum_{m=0}^{N/2 – 1} x_{2m + 1} \cdot e^{-i~2\pi~k~(2m + 1)~/~N} \\
&= \sum_{m=0}^{N/2 – 1} x_{2m} \cdot e^{-i~2\pi~k~m~/~(N/2)} + e^{-i~2\pi~k~/~N} \sum_{m=0}^{N/2 – 1} x_{2m + 1} \cdot e^{-i~2\pi~k~m~/~(N/2)}
\end{align} $$

در این حالت، تبدیل فوریه گسسته تکی را به دو عبارت تقسیم کردیم که هر کدام شباهت بسیار زیادی به عبارت تبدیل فوریه اصلی دارند و یکی بر روی اعداد فرد و دیگری بر روی اعداد زوج عمل می‌کنند. اما تا این قسمت هنوز هیچ توان محاسباتی را کاهش نداده‌ایم و هر عبارت از $$ (N/2)*N $$ محاسبه تشکیل شده است که در مجموع $$ N^2 $$ محاسبه را شامل می‌شود.

آن‌چه موجب کاهش هزینه محاسباتی می‌شود، استفاده از خاصیت تقارن در هر یک از عبارت‌های محاسبه شده است. زیرا بازه $$ k $$ برابر با $$ 0 \le k < N $$ است، در حالی که بازه $$ n $$ برابر با $$ 0 \le n < M \equiv N/2 $$ در نظر گرفته می‌شود. در خاصیت تقارن بالا نکته‌ای که وجود دارد این است که می‌توان برای هر زیر مسئله (Sub-Problem) فقط نیمی از محاسبات را انجام داد. بنابراین محاسبات $$ \mathcal{O}[N^2] $$ تبدیل به $$ \mathcal{O}[M^2] $$ می‌شود که $$ M $$ برابر با نصف اندازه $$ N $$ است.

اما روند کار در اینجا متوقف نمی‌شود. تا زمانی که تبدیل فوریه کوچک‌تر دارای مقدار M زوج باشد، می‌توانیم این روش تقسیم و غلبه (Divide-and-Conquer) را به صورت تکراری انجام دهیم و هر بار هزینه محاسباتی را نصف کنیم. این روند را تا جایی ادامه می‌دهیم که آرایه به دست آمده آنقدر کوچک باشد که استفاده از این استراتژی دیگر تاثیری در بهبود محاسبات نداشته باشد.

مثالی از تبدیل فوریه سریع با $$ N=8 $$

فرض کنید که $$ x(n) $$ دنباله‌ای متشکل از ۸ مقدار باشد. با استفاده از فرمول تبدیل فوریه گسسته، می‌توانیم مقدار DFT این سیگنال را به صورت زیر به دست آوریم:

$$ X\left(k\right)=x(0){{e}^{-j\tfrac{2\pi }{8}k\times0}}+x(1){{e}^{-j\tfrac{2\pi }{8}k\times1}}+x(2){{e}^{-j\tfrac{2\pi }{8}k\times2}}+\dots +x(7){{e}^{-j\tfrac{2\pi }{8}k\times7}} $$

همان طور که در بالا بیان شد، هدف این است که بتوانیم این دنباله هشت نقطه‌ای را ابتدا توسط دو عبارت با طول کوتاه‌تر بازنویسی کنیم. طول DFT در این حالت برابر با $$ N=8 $$ است که در مخرج عبارت نمایی مختلط ظاهر می‌شود. در ایده تبدیل فوریه سریع، می‌خواهیم برخی از عبارت‌های معادله تبدیل فوریه گسسته را به نحوی گروه‌بندی کنیم که کسر $$ -\tfrac{j2\pi}{8}kn $$ ساده‌تر شود.

بنابراین، DFTهایی با طول کوتاه‌تر را از فرمول اصلی استخراج می‌کنیم. مثلا در این حالت که N عددی زوج است، تمام عبارت‌ها با اندیس نمونه زوج، یعنی $$ x(4) $$ و $$ x(2) $$ و $$ x(0) $$ و $$ x(6) $$ را انتخاب می‌کنیم. بنابراین عبارت زیر را به دست می‌آوریم.

$$ G\left(k\right)=x(0){{e}^{-j\tfrac{2\pi }{8}k\times0}}+x(2){{e}^{-j\tfrac{2\pi }{8}k\times2}}+x(4){{e}^{-j\tfrac{2\pi }{8}k\times4}}+x(6){{e}^{-j\tfrac{2\pi }{8}k\times6}} $$

پس از ساده‌سازی کسرها در عبارات مختلط، مقدار زیر محاسبه می‌گردد:

$$ G\left(k\right)=x(0){{e}^{-j\tfrac{2\pi }{4}k\times0}}+x(2){{e}^{-j\tfrac{2\pi }{4}k\times1}}+x(4){{e}^{-j\tfrac{2\pi }{4}k\times2}}+x(6){{e}^{-j\tfrac{2\pi }{4}k\times3}} $$

با مقایسه این عبارت با فرمول اصلی محاسبه DFT مشاهده می‌کنیم که $$ G\left(k\right) $$ یک تبدیل فوریه گسسته ۴ نقطه‌ای متشکل از $$ x(4) $$ و $$ x(2) $$ و $$ x(0) $$ و $$ x(6) $$ است. تا این قسمت، نشان دادیم که نصف محاسبات در فرمول اولیه را می‌توانیم با محاسبه ۴ نقطه از تبدیل فوریه گسسته حذف کنیم. اما برای مابقی محاسبات، که متعلق به نمونه‌های با اندیس فرد هستند، عبارت زیر را داریم:

$$ H_{1}\left(k\right)=x(1){{e}^{-j\tfrac{2\pi }{8}k\times1}}+x(3){{e}^{-j\tfrac{2\pi }{8}k\times3}}+x(5){{e}^{-j\tfrac{2\pi }{8}k\times5}}+x(7){{e}^{-j\tfrac{2\pi }{8}k\times7}} $$

برای ساده‌سازی $$ -\tfrac{j2\pi}{8}kn $$، می‌توانیم از $$ e^{-j\tfrac{2\pi}{8}k} $$ فاکتور بگیریم و عبارت بالا را بازنویسی کنیم:

$$ H_{1}\left(k\right)= {{e}^{-j\tfrac{2\pi }{8}k\times1}}\left( x(1){{e}^{-j\tfrac{2\pi }{8}k\times0}}+x(3){{e}^{-j\tfrac{2\pi }{8}k\times2}}+x(5){{e}^{-j\tfrac{2\pi }{8}k\times4}}+x(7){{e}^{-j\tfrac{2\pi }{8}k\times6}} \right) $$

مقدار بالا را مجددا ساده‌سازی می‌کنیم:

$$ H_{1}\left(k\right)= {{e}^{-j\tfrac{2\pi }{8}k\times1}}\left( x(1){{e}^{-j\tfrac{2\pi }{4}k\times0}}+x(3){{e}^{-j\tfrac{2\pi }{4}k\times1}}+x(5){{e}^{-j\tfrac{2\pi }{4}k\times2}}+x(7){{e}^{-j\tfrac{2\pi }{4}k\times3}} \right) $$

حال بار دیگر این فرمول را با فرمول اولیه برای محاسبه DFT مقایسه می‌کنیم و می‌بینیم که عبارت از ضرب DFT چهار نقطه یعنی $$ x(۵) $$ و $$ x(۳) $$ و $$ x(۱) $$ و $$ x(۷) $$ به دست آمده است. بنابراین، به هدف محاسبه DFT هشت نقطه‌ای با استفاده از دو DFT کوتاه‌تر ۴ نقطه‌ای رسیدیم. نتیجه نهایی را می‌توان به صورت زیر نمایش داد:

$$ X\left(k\right)=G\left(k\right)+{{e}^{-j\tfrac{2\pi }{8}k\times1}}H\left(k\right) $$

که در این فرمول، $$ G(k) $$ و $$ H(k) $$ متناظر با تبدیل فوریه گسسته ۴ نقطه‌ای هستند. اما سوالی که به وجود می‌آید این است که چگونه $$ G(k)+e^{-\tfrac{j2\pi}{8}k \times 1}H(k) $$ بار محاسباتی را کاهش می‌دهد، در حالی که به تعداد برابری ضرب حقیقی در مقایسه با $$ X(k) $$ در فرمول اصلی نیاز دارد؟ در واقع ما فقط فرمول را بازآرایی کردیم و فاکتور ضرایب را تغییر دادیم، اما تعداد ضرب‌ها اصلا کاهش نیافته‌اند.

برای حل این تضاد ظاهری، باید سه نکته را به یاد داشته باشیم. اولا، یک عبارت نمایی مختلط گسسته $$ e^{-\tfrac{j2\pi}{N}kn} $$ یک تابع متناوب از k با تناوب N است. دوما، بازه k در این مثال از ۰ تا ۷ است.

سوما، زمانی که معادله $$ X\left(k\right)=x(0){{e}^{-j\tfrac{2\pi }{8}k\times0}}+x(1){{e}^{-j\tfrac{2\pi }{8}k\times1}}+x(2){{e}^{-j\tfrac{2\pi }{8}k\times2}}+\dots +x(7){{e}^{-j\tfrac{2\pi }{8}k\times7}} $$ متشکل از عبارات نمایی با تناوب ۸، یعنی $$ e^{-j\tfrac{2\pi}{8}kn} $$ باشد، آن‌گاه معادله $$ X\left(k\right)=G\left(k\right)+{{e}^{-j\tfrac{2\pi }{8}k\times1}}H\left(k\right) $$ متشکل از دو تبدیل فوریه گسسته ۴ نقطه|‌ی $$ G(k) $$ و $$ H(k) $$ است که مجموع عبارات نمایی مختلط با تناوب ۴ هستند.

این رفتار متناوب، به ما اجازه می‌دهد تا پیچیدگی محاسباتی کلی را کاهش دهیم.

به عنوان مثال، زمانی که $$ X(k) $$ و $$ X(k+4) $$ را محاسبه می‌کنیم، بر اساس معادله اول، مجبوریم که عبارات معادله را دو بار حساب کنیم. اما با استفاده از معادله دوم که به دست آوردیم، داریم:

$$ X\left(k\right)=G\left(k\right)+{{e}^{-j\tfrac{2\pi }{8}k\times1}}H\left(k\right) $$

$$ X\left(k+4\right)=G\left(k+4\right)+{{e}^{-j\tfrac{2\pi }{8}(k+4)\times1}}H\left(k+4\right) $$

چون $$ G(k) $$ و $$ H(k) $$ متناوب با دوره تناوب ۴ هستند، بنابراین معادله آخر را می‌توان به صورت زیر بازنویسی کرد:

$$ X\left(k+4 \right)=G\left(k\right)+{{e}^{-j\tfrac{2\pi }{8}\left (k+4 \right) \times1}}H\left(k\right) $$

با مقایسه این معادله با معادله اصلی تبدیل فوریه گسسته، مشخص می‌شود که چگونه شکستن DFT هشت نقطه‌ای به دو DFT چهار نقطه‌ای، باعث می‌شود از محاسباتی تقریبا یکسان برای $$ X(k) $$ و $$ X(k+4) $$ استفاده کنیم. در نتیجه به صورت قابل توجهی تعداد محاسبات از طریق مشخصه تناوب این توابع، کاهش می‌یابد.

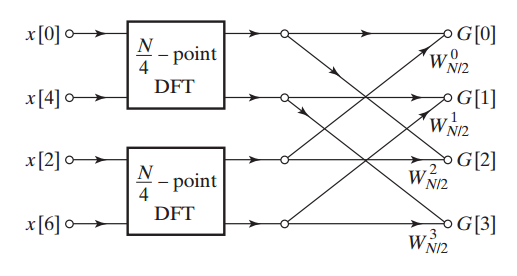
تصویر زیر نمایی از تجزیه تبدیل فوریه گسسته ۸ نقطه‌ای به دو تبدیل فوریه ۴ نقطه‌ای را نشان می‌دهد. در این نمودار $$ W_{N}^{k}=e^{-j\tfrac{2\pi}{N}k} $$ است.

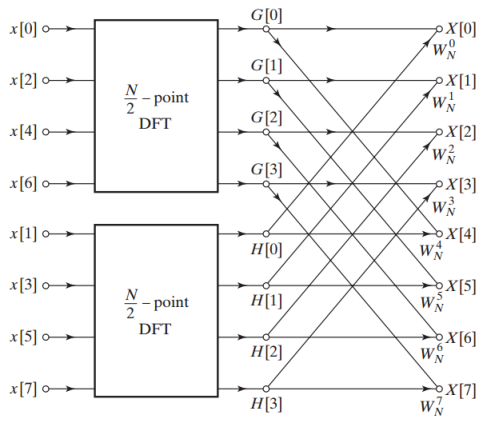
زمانی که از معادله اصلی تبدیل فوریه گسسته استفاده می‌کنیم، نیاز است تا از $$ 4N^2=256 $$ ضرب حقیقی برای هشت نقطه استفاده کنیم، در حالی که با الگوریتم توضیح داده شده، می‌توان دو تبدیل فوریه ۴ نقطه‌ای را با استفاده از N ضرب مختلط و $$ 2\times 4 \times (\tfrac{N}{2})^2=2\times 4 \times 4^2=128 $$ ضرب حقیقی محاسبه کرد. N ضرب مختلط خود به $$ 4N=4 \times 8=32 $$ ضرب حقیقی نیاز دارند. بنابراین الگوریتم در حالت کلی به ۱۶۰ ضرب حقیقی نیاز دارد. این عدد در مقایسه با 256 ضرب حقیقی در حالت قبلی، کمتر است. این بهبود قابل توجهی است، اما می‌توان از طریق اعمال روش یاد شده به DFT چهار نقطه‌ای به بهبود بیشتری نیز دست یافت. دیدیم که نقطه شروع الگوریتم، طول DFT است که زوج در نظر گرفته می‌شود و ما قادریم که عبارت نمایی مختلط از اندیس زوج را ساده کنیم. به همین دلیل، برای اینکه بار دیگر الگوریتم را ساده‌سازی کنیم، نیاز داریم که $$ \tfrac{N}{2} $$ مضربی از دو باشد. در این مثال خاص، $$ \tfrac{N}{2}=4 $$ است و با استفاده از الگوریتم بالا می‌توانیم هر کدام از دو تبدیل فوریه ۴ نقطه‌ای را به دو تبدیل فوریه ۲ نقطه‌ای تجزیه کنیم. به عنوان مثال، تبدیل فوریه گسسته $$ \tfrac{N}{2} $$ نقطه اولی در نمودار شکل بالا را می‌توان به صورت زیر نشان داد.

با جایگذاری نمودار بالا در هر کدام از تبدیل فوریه‌های گسسته ۴ نقطه‌ای، می‌توان به نمودار جدید زیر رسید.

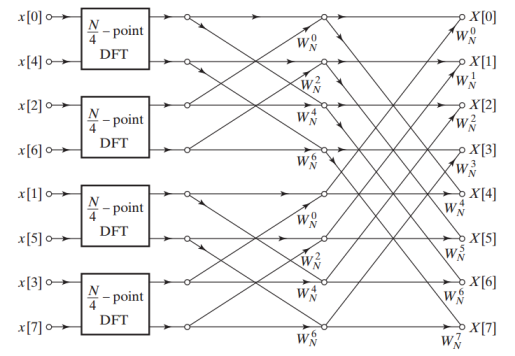
توجه داشته باشید که این نمودار، هر کدام از ضرایب $$ W_{\tfrac{N}{2}} $$ را با ضریب $$ W_{N}^{2} $$ جایگزین می‌کند؛ زیرا $$ e^{-j\tfrac{2\pi}{(\tfrac{N}{2})}}=e^{-j\tfrac{2\pi}{N} \times 2}  $$ است.

سرانجام، می‌توانیم تبدیل فوریه دو نقطه‌ای در تصویر بالا را نیز با نمودار زیر جایگزین کنیم.

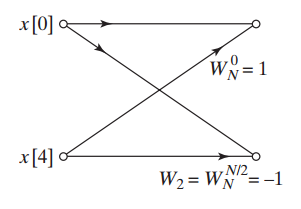
بعد از جایگذاری، در نهایت به نمودار زیر می‌رسیم.

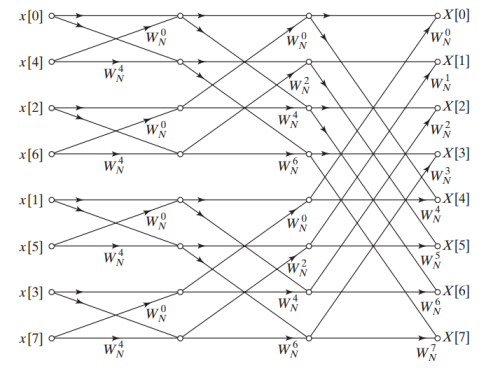
در مثال بررسی شده، نشان داده شد که به منظور پیاده‌سازی تکنیک به صورت تکراری، تا زمان باقی ماندن تبدیل فوریه گسسته دو نقطه‌ای، باید طول تبدیل فوریه گسسته اصلی را از توان دو انتخاب کنیم. به عبارت دیگر باید $$ N=2^{\nu} $$ برقرار باشد. در این حالت پس از $$ log_{2}(N) $$ تکرار، به دو تبدیل فوریه گسسته دو نقطه‌ای می‌رسیم. همان‌ طور که از تصویر آخر نیز می‌توان مشاهده کرد، هر گام از الگوریتم به $$ Nlog_{2}(N) $$ ضرب مختلط نیاز دارد. مثلا در مورد تبدیل فوریه هشت نقطه‌ای $$ 8log_{2}(8)=24 $$ ضرب مختلط و $$ 24 \times 4=96 $$ ضرب حقیقی نیاز داریم، در حالی که محاسبه مستقیم این DFT به ۲۵۶ ضرب حقیقی نیاز دارد. بنابراین در محاسبه تبدیل فوریه گسسته برای داده‌های طولانی، این الگوریتم می‌تواند منجر به کاهش محاسبات به اندازه قابل توجهی شود.

پیاده‌سازی بازگشتی تبدیل فوریه سریع

این روش بازگشتی را می‌توان در پایتون به سادگی پیاده‌سازی کرد. همان طور که در قسمت قبل هم بیان شد، تبدیل فوریه گسسته را می‌توان به صورت زیر در پایتون اجرا کرد:

import numpy as np
def DFT_slow(x):
    """Compute the discrete Fourier Transform of the 1D array x"""
    x = np.asarray(x, dtype=float)
    N = x.shape[0]
    n = np.arange(N)
    k = n.reshape((N, 1))
    M = np.exp(-2j * np.pi * k * n / N)
    return np.dot(M, x)

حال تبدیل فوریه سریع به صورت زیر نوشته می‌شود:

def FFT(x):
    """A recursive implementation of the 1D Cooley-Tukey FFT"""
    x = np.asarray(x, dtype=float)
    N = x.shape[0]
    
    if N % 2 > 0:
        raise ValueError("size of x must be a power of 2")
    elif N <= 32:  # this cutoff should be optimized
        return DFT_slow(x)
    else:
        X_even = FFT(x[::2])
        X_odd = FFT(x[1::2])
        factor = np.exp(-2j * np.pi * np.arange(N) / N)
        return np.concatenate([X_even + factor[:N / 2] * X_odd,
                               X_even + factor[N / 2:] * X_odd])

با استفاده از قطعه کد زیر می‌توان از صحیح بودن برنامه نوشته شده اطمینان حاصل کرد:

x = np.random.random(1024)
np.allclose(FFT(x), np.fft.fft(x))

خروجی این کد True است.

می‌توانیم زمان اجرای این برنامه را توسط کد زیر محاسبه کرد:

%timeit DFT_slow(x)
%timeit FFT(x)
%timeit np.fft.fft(x)

خروجی کد به صورت زیر است:

10 loops, best of 3: 77.6 ms per loop
100 loops, best of 3: 4.07 ms per loop
10000 loops, best of 3: 24.7 µs per loop

این روش دارای سرعت بسیار بالاتری نسبت به ورژن اصلی تبدیل فوریه گسسته است. الگوریتم بازگشتی به صورت مجانبی $$ \mathcal{O}[N\log N] $$ است. آن‌چه که پیاده‌سازی شد، تبدیل فوریه سریع نام دارد.

به این نکته توجه کنید که هنوز با سرعت الگوریتم توکار (Built-in) برای FFT در پکیج numpy فاصله داریم و البته این اختلاف امری قابل پیش بینی است. الگوریتم FFTPACK در پکیج numpy یک پیاده‌سازی در فورترن (Fortran) است که حاصل سال‌ها تنظیم و بهینه‌سازی است. علاوه بر این، از آنجایی که برنامه پیشنهادی ما (که مبتنی بر کتابخانه Numpy است.) از فرایندهایی بازگشتی پشته‌ای (Python-Stack Recursion) (مبتنی بر پشته) و اختصاص حافظه به تعداد زیادی از آرایه‌های موقت (Temporary Array) در زبان پایتون استفاده می‌کند، بار محاسباتی قابل توجهی به سیستم تحمیل می‌شود.

یک استراتژی مناسب برای افزایش سرعت اجرای کد نوشته شده برای تبدیل فوریه سریع، استفاده از محاسبات برداری تا حد امکان است. برای اجرای کد بالا می‌توانیم از این روش استفاده کنیم و فراخوانی توابع بازگشتی را حذف کنیم و برنامه FFT در پایتون را حتی از این هم سریع‌تر و کاراتر کنیم.

پیاده‌سازی تبدیل فوریه سریع با استفاده از محاسبات برداری

به این نکته توجه کنید که در پیاده‌سازی FFT به روش بازگشتی، در پایین‌ترین سطح بازگشت، حاصلضرب بردار در ماتریس را انجام دادیم. کارایی الگوریتم در این حالت می‌تواند با استفاده از محاسبه ضرب بردار در ماتریس به صورت ضرب یکباره ماتریس در ماتریس بهبود یابد. همچنین، در هر مرحله از برنامه، عملیات تکراری انجام می‌گیرد که می‌تواند توسط محاسبات برداری انجام شود. پکیج numpy در این نوع محاسبات بسیار عالی عمل می‌کند و ما نیز می‌توانیم از این ویژگی استفاده کنیم و ورژن برداری برنامه تبدیل فوریه سریع را پیاده‌سازی کنیم.

def FFT_vectorized(x):
    """A vectorized, non-recursive version of the Cooley-Tukey FFT"""
    x = np.asarray(x, dtype=float)
    N = x.shape[0]

    if np.log2(N) % 1 > 0:
        raise ValueError("size of x must be a power of 2")

    # N_min here is equivalent to the stopping condition above,
    # and should be a power of 2
    N_min = min(N, 32)
    
    # Perform an O[N^2] DFT on all length-N_min sub-problems at once
    n = np.arange(N_min)
    k = n[:, None]
    M = np.exp(-2j * np.pi * n * k / N_min)
    X = np.dot(M, x.reshape((N_min, -1)))

    # build-up each level of the recursive calculation all at once
    while X.shape[0] < N:
        X_even = X[:, :X.shape[1] / 2]
        X_odd = X[:, X.shape[1] / 2:]
        factor = np.exp(-1j * np.pi * np.arange(X.shape[0])
                        / X.shape[0])[:, None]
        X = np.vstack([X_even + factor * X_odd,
                       X_even - factor * X_odd])

    return X.ravel()

برنامه در این حالت اندکی مبهم است، اما در واقع یک بازآرایی مجدد از عملگرهای استفاده شده در ورژن بازگشتی برنامه است، با این تفاوت که این بار از تقارن در محاسبه factor استفاده کرده‌ایم و تنها نصفی از آرایه را محاسبه کرده‌ایم. مجددا برای اطمینان از صحت کارکرد برنامه کد زیر را اجرا می‌کنیم:

x = np.random.random(1024)
np.allclose(FFT_vectorized(x), np.fft.fft(x))

خروجی این قطعه کد نیز True است. برای اثبات این مسئله که الگوریتم دارای کارکرد بهینه‌تری است، می‌توان با استفاده از کد زیر بر روی یک آرایه بسیار بزرگ، زمان اجرای این برنامه با برنامه‌های حالت‌های قبل را مقایسه کرد:

x = np.random.random(1024 * 16)
%timeit FFT(x)
%timeit FFT_vectorized(x)
%timeit np.fft.fft(x)

خروجی این کد به صورت زیر خواهد بود:

10 loops, best of 3: 72.8 ms per loop
100 loops, best of 3: 4.11 ms per loop
1000 loops, best of 3: 505 µs per loop

همان طور که دیده می‌شود، خروجی این برنامه نسبت به برنامه قبل بهبود یافته است، اما باز هم نسبت به تابع توکار numpy زمان زیادی را برای محاسبات لازم دارد.

طیف فرکانسی تبدیل فوریه سریع

برای درک تاثیر استفاده از تبدیل فوریه سریع، ابتدا کد زیر را برای ایجاد یک سیگنال فرضی در پایتون اجرا می‌کنیم. توسط این کد ابتدا سیگنالی را تعریف می‌کنیم که حاصل جمع دو سیگنال سینوسی باشد. یکی از این سیگنال‌ها فرکانس ۴۰ هرتز و دیگری فرکانس ۹۰ هرتز دارد.

t = np.linspace(0, 0.5, 500)
s = np.sin(40 * 2 * np.pi * t) + 0.5 * np.sin(90 * 2 * np.pi * t)

plt.ylabel("Amplitude")
plt.xlabel("Time [s]")
plt.plot(t, s)
plt.show()

تصویر زیر، سیگنال را در حوزه زمان نشان می‌دهد.

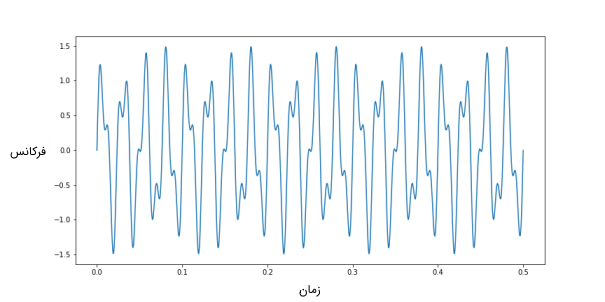
برای به دست آوردن طیف فرکانسی سیگنال زمانی به دست آمده در بالا، باید از سیگنال تبدیل فوریه سریع بگیریم. قطعه کد زیر این کار را با استفاده از تابع توکار پایتون انجام می‌دهد.

fft = np.fft.fft(s)


for i in range(2):
    print("Value at index {}:\t{}".format(i, fft[i + 1]), "\nValue at index {}:\t{}".format(fft.size -1 - i, fft[-1 - i]))

خروجی این کد به صورت زیر خواهد بود.

Value at index 0: (0.0003804834928402556-0.060555031761900024j) 
Value at index 499: (0.0003804834928403944+0.060555031761903175j)
Value at index 1: (0.0015317714831371565-0.12188808528069561j) 
Value at index 498: (0.0015317714831373785+0.1218880852806919j)

در قطعه کد بالا، تبدیل فوریه سریع دو سیگنال سینوسی با فرکانس های متفاوت را به دست آوردیم و سپس دو مقدار اول و دو مقدار آخر دنباله تبدیل فوریه سریع را در خروجی نشان دادیم. همان طور که دیده می‌شود، این مقادیر اعداد مختلط هستند. اگر مقدار اول در این دنباله، که با اندیس ۰ نشان داده شده است را با آخرین عدد از دنباله، که با اندیس ۴۹۹ نشان داده شده است، مقایسه کنیم، می‌توانیم به این نکته پی ببریم که قسمت حقیقی هر دو عدد با یکدیگر برابر هستند و مقدار موهومی این اعداد هم دامنه برابری دارند و فقط در علامت متفاوت هستند، یکی از آن‌ها مثبت و دیگری منفی است. در واقع اعداد مختلط مزدوج هستند. این قاعده برای تمام اعداد در دنباله FFT صادق است.

به دلیل این که نیمه دوم دنباله، هیچ اطلاعات جدیدی را به ما نمی‌دهد، پس می‌توانیم نتیجه بگیریم که نیمه اول دنباله FFT، همان خروجی مورد نظر ما محسوب می‌شود. اعداد خروجی مختلط حاوی اطلاعات زیر هستند:

• دامنه مربوط به فرکانس‌های خاصی از موج سینوسی که نشان دهنده انرژی سیگنال هستند.
• انحراف فاز مربوط به فرکانس‌های خاصی از موج سینوسی.

دامنه را می‌توان با محاسبه قدر مطلق اعداد خروجی و انحراف فاز را با محاسبه زاویه اعداد به دست آورد.

انرژی هر فرکانس از اهمیت بالایی برخوردار است، بنابراین می‌توان مقدار مطلق خروجی تبدیل فوریه سریع را محاسبه کرد. برای به دست آوردن درک بهتر از طیف، باید انرژی را بر حسب فرکانس ترسیم کنیم. هر خروجی عدد گسسته FFT، متناظر با یک فرکانس خاص است. رزولوشن فرکانسی توسط فرمول زیر محاسبه می‌شود:

$$ \Delta f = \frac{f_s}{N} $$

با کنار هم گذاشتن تمام موارد، می‌توانیم طیف فرکانسی در مثال ساده سیگنال سینوسی را به دست آوریم. لازم است تا فقط نصفی از طیف را ترسیم کنیم؛ زیرا تمام اطلاعات در همین نیمه به دست می‌آید. قطعه کد زیر را در پایتون اجرا می‌کنیم:

fft = np.fft.fft(s)
T = t[1] - t[0]  # sampling interval 
N = s.size

# 1/T = frequency
f = np.linspace(0, 1 / T, N)

plt.ylabel("Amplitude")
plt.xlabel("Frequency [Hz]")
plt.bar(f[:N // 2], np.abs(fft)[:N // 2] * 1 / N, width=1.5)  # 1 / N is a normalization factor
plt.show()

تصویر زیر به عنوان خروجی این کد ترسیم می‌شود.

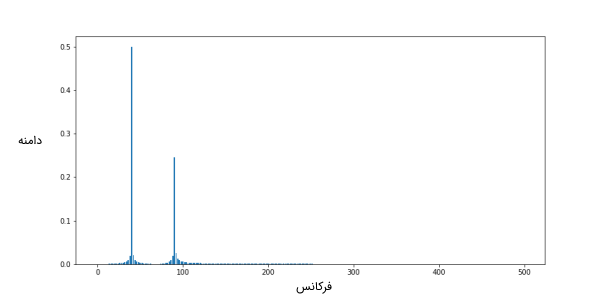
همان طور که می‌بینیم، تبدیل FFT سیگنال به دست می‌آید و اطلاعاتی راجع به فرکانس‌های امواجی که در حوزه زمان بودند، در اختیار ما قرار می‌دهد. FFT یک مبادله بین اطلاعات در حوزه زمان و اطلاعات در حوزه فرکانس است. با گرفتن تبدیل FFT از یک سیگنال در حوزه زمان، تمام اطلاعات زمانی سیگنال را از دست داده و در عوض اطلاعات فرکانسی آن را به دست می‌آوریم. برای داشتن اطلاعات هم در حوزه زمان و هم در حوزه فرکانس در یک طیف، باید از طیف نگاره (Spectrogram) استفاده کنیم.

تصویر زیر FFT یک سیگنال موسیقی را نشان می‌دهد.

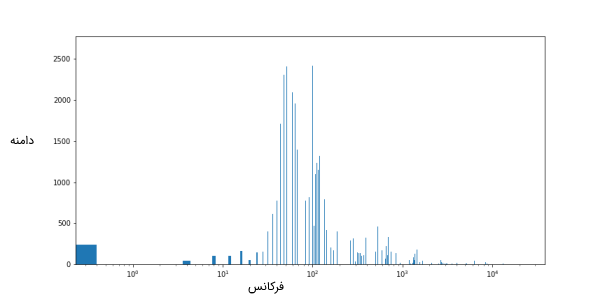
فرکانس این نمودار در مقیاس لگاریتمی ترسیم شده است. همان طور که در تصویر دیده می‌شود فرکانس غالب این سیگنال بین $$ 10^{1.5} $$ و $$ 10^{2.2} $$ هرتز (30 تا 158 هرتز) است. اگر مطابق مثال ابتدای متن، پنجره‌ای با فرکانس طبیعی 100 هرتز داشته باشیم، آن‌گاه می‌توان به این نکته پی برد که فرکانس طبیعی پنجره دقیقا در میان این بازه فرکانسی غالب سیگنال صوتی است و با بالا بردن صدای موسیقی، این امکان وجود دارد که پدیده رزونانس به وجود بیاید.

برنامه تبدیل فوریه سریع در جاوا

با استفاده از برنامه زیر می‌توان تبدیل فوریه سریع را در زبان برنامه‌نویسی جاوا محاسبه کرد.

/* 
 * Free FFT and convolution (Java)
 


public final class Fft {
	
	/* 
	 * Computes the discrete Fourier transform (DFT) of the given complex vector, storing the result back into the vector.
	 * The vector can have any length. This is a wrapper function.
	 */
	public static void transform(double[] real, double[] imag) {
		int n = real.length;
		if (n != imag.length)
			throw new IllegalArgumentException("Mismatched lengths");
		if (n == 0)
			return;
		else if ((n & (n - 1)) == 0)  // Is power of 2
			transformRadix2(real, imag);
		else  // More complicated algorithm for arbitrary sizes
			transformBluestein(real, imag);
	}
	
	
	/* 
	 * Computes the inverse discrete Fourier transform (IDFT) of the given complex vector, storing the result back into the vector.
	 * The vector can have any length. This is a wrapper function. This transform does not perform scaling, so the inverse is not a true inverse.
	 */
	public static void inverseTransform(double[] real, double[] imag) {
		transform(imag, real);
	}
	
	
	/* 
	 * Computes the discrete Fourier transform (DFT) of the given complex vector, storing the result back into the vector.
	 * The vector's length must be a power of 2. Uses the Cooley-Tukey decimation-in-time radix-2 algorithm.
	 */
	public static void transformRadix2(double[] real, double[] imag) {
		// Length variables
		int n = real.length;
		if (n != imag.length)
			throw new IllegalArgumentException("Mismatched lengths");
		int levels = 31 - Integer.numberOfLeadingZeros(n);  // Equal to floor(log2(n))
		if (1 << levels != n)
			throw new IllegalArgumentException("Length is not a power of 2");
		
		// Trigonometric tables
		double[] cosTable = new double[n / 2];
		double[] sinTable = new double[n / 2];
		for (int i = 0; i < n / 2; i++) {
			cosTable[i] = Math.cos(2 * Math.PI * i / n);
			sinTable[i] = Math.sin(2 * Math.PI * i / n);
		}
		
		// Bit-reversed addressing permutation
		for (int i = 0; i < n; i++) {
			int j = Integer.reverse(i) >>> (32 - levels);
			if (j > i) {
				double temp = real[i];
				real[i] = real[j];
				real[j] = temp;
				temp = imag[i];
				imag[i] = imag[j];
				imag[j] = temp;
			}
		}
		
		// Cooley-Tukey decimation-in-time radix-2 FFT
		for (int size = 2; size <= n; size *= 2) {
			int halfsize = size / 2;
			int tablestep = n / size;
			for (int i = 0; i < n; i += size) {
				for (int j = i, k = 0; j < i + halfsize; j++, k += tablestep) {
					int l = j + halfsize;
					double tpre =  real[l] * cosTable[k] + imag[l] * sinTable[k];
					double tpim = -real[l] * sinTable[k] + imag[l] * cosTable[k];
					real[l] = real[j] - tpre;
					imag[l] = imag[j] - tpim;
					real[j] += tpre;
					imag[j] += tpim;
				}
			}
			if (size == n)  // Prevent overflow in 'size *= 2'
				break;
		}
	}
	
	
	/* 
	 * Computes the discrete Fourier transform (DFT) of the given complex vector, storing the result back into the vector.
	 * The vector can have any length. This requires the convolution function, which in turn requires the radix-2 FFT function.
	 * Uses Bluestein's chirp z-transform algorithm.
	 */
	public static void transformBluestein(double[] real, double[] imag) {
		// Find a power-of-2 convolution length m such that m >= n * 2 + 1
		int n = real.length;
		if (n != imag.length)
			throw new IllegalArgumentException("Mismatched lengths");
		if (n >= 0x20000000)
			throw new IllegalArgumentException("Array too large");
		int m = Integer.highestOneBit(n) * 4;
		
		// Trignometric tables
		double[] cosTable = new double[n];
		double[] sinTable = new double[n];
		for (int i = 0; i < n; i++) {
			int j = (int)((long)i * i % (n * 2));  // This is more accurate than j = i * i
			cosTable[i] = Math.cos(Math.PI * j / n);
			sinTable[i] = Math.sin(Math.PI * j / n);
		}
		
		// Temporary vectors and preprocessing
		double[] areal = new double[m];
		double[] aimag = new double[m];
		for (int i = 0; i < n; i++) {
			areal[i] =  real[i] * cosTable[i] + imag[i] * sinTable[i];
			aimag[i] = -real[i] * sinTable[i] + imag[i] * cosTable[i];
		}
		double[] breal = new double[m];
		double[] bimag = new double[m];
		breal[0] = cosTable[0];
		bimag[0] = sinTable[0];
		for (int i = 1; i < n; i++) {
			breal[i] = breal[m - i] = cosTable[i];
			bimag[i] = bimag[m - i] = sinTable[i];
		}
		
		// Convolution
		double[] creal = new double[m];
		double[] cimag = new double[m];
		convolve(areal, aimag, breal, bimag, creal, cimag);
		
		// Postprocessing
		for (int i = 0; i < n; i++) {
			real[i] =  creal[i] * cosTable[i] + cimag[i] * sinTable[i];
			imag[i] = -creal[i] * sinTable[i] + cimag[i] * cosTable[i];
		}
	}
	
	
	/* 
	 * Computes the circular convolution of the given real vectors. Each vector's length must be the same.
	 */
	public static void convolve(double[] x, double[] y, double[] out) {
		int n = x.length;
		if (n != y.length || n != out.length)
			throw new IllegalArgumentException("Mismatched lengths");
		convolve(x, new double[n], y, new double[n], out, new double[n]);
	}
	
	
	/* 
	 * Computes the circular convolution of the given complex vectors. Each vector's length must be the same.
	 */
	public static void convolve(double[] xreal, double[] ximag,
			double[] yreal, double[] yimag, double[] outreal, double[] outimag) {
		
		int n = xreal.length;
		if (n != ximag.length || n != yreal.length || n != yimag.length
				|| n != outreal.length || n != outimag.length)
			throw new IllegalArgumentException("Mismatched lengths");
		
		xreal = xreal.clone();
		ximag = ximag.clone();
		yreal = yreal.clone();
		yimag = yimag.clone();
		transform(xreal, ximag);
		transform(yreal, yimag);
		
		for (int i = 0; i < n; i++) {
			double temp = xreal[i] * yreal[i] - ximag[i] * yimag[i];
			ximag[i] = ximag[i] * yreal[i] + xreal[i] * yimag[i];
			xreal[i] = temp;
		}
		inverseTransform(xreal, ximag);
		
		for (int i = 0; i < n; i++) {  // Scaling (because this FFT implementation omits it)
			outreal[i] = xreal[i] / n;
			outimag[i] = ximag[i] / n;
		}
	}
	
}

تبدیل فوریه سریع در زبان متلب

با استفاده از برنامه زیر می‌توان تبدیل فوریه سریع را در زبان متلب محاسبه کرد.

function [spectrum, freq] = autofft(xs, ts, fftset)

%% nargin check
if nargin < 2
    error('Not enough input arguments.');
elseif nargin > 3
    error('Too many input arguments.');
end
%
%% Convert row vectors to column vectors if needed
if size(xs, 1) == 1         % samples
    xs = xs(:);                     
end
if size(ts(:), 1) == 1      % sampling frequency
	fs = ts;                    
else
    fs = 1 / (ts(2) - ts(1)); 
end
%
%% Specify default fftset
defset = struct('nwin', size(xs, 1), ...
                'twin', size(xs, 1) / fs, ...
                'overlap', 50, ...
                'lowpass', fs/2, ...
                'window', 'u', ...
                'averaging', 'lin', ...
                'jw', '1', ...
                'unit', 'pow');
deffields = fieldnames(defset);
%
%% Set analyser parameters
if nargin == 2  % use default fftset
    fftset = defset;
else            % use user-defined fftset  
    % Check whether there is user-defined 'nwin' or 'twin' parameter
    if isfield(fftset, 'nwin')
        fftset.twin = fftset.nwin / fs;
    elseif isfield(fftset, 'twin')
        fftset.nwin = round(fftset.twin * fs);
    end
    % Set unspecified parameters to default
    for i = 1:numel(deffields)        
        if isfield(fftset, deffields{i}) == 0
            fftset.(deffields{i}) = defset.(deffields{i});
        end
    end
end
% Generate frequency vector
freq = (fs * (0:(fftset.nwin/2)) / fftset.nwin)';
% Set allowed frequencies for the low-pass filtering
freq = freq(freq <= fftset.lowpass);
% Set handling of the last spectral line
if freq(end) == fs/2
    sh = 1; % Nyquist frequency is at the last spectral line
else
	sh = 0; % Nyquist frequency is not at the last spectral line
end
% Set number of overlaping samples
fftset.overlap = round(fftset.nwin * fftset.overlap / 100);
% Set indices for the signal segmentation
imax = floor((size(xs, 1)-fftset.overlap) / (fftset.nwin-fftset.overlap));
                                                % number of windows
ind = zeros(imax,2);                            % matrix of indices
ni = 1;                                         % pointer
for i = 1:imax                                  % cycle through windows
    ind(i,1) = ni; 
    ni = ni + fftset.nwin - 1;
    ind(i,2) = ni;
    ni = ni - fftset.overlap + 1;
end
% Generate the time weighting window
[fftset.window, fftset.noiseband] = timeweight(fftset.window, fftset.nwin, fs);
% Set constant for the jw weigthing
switch lower(fftset.jw)
    case '1/jw2'
        fftset.jw = - 1 ./ (4 * pi^2 * freq.^2);
    case '1/jw'
        fftset.jw = 1 ./ (2i * pi * freq);
    case 'jw'
        fftset.jw = 2i * pi * freq;
    case 'jw2'
        fftset.jw = - 4 * pi^2 * freq.^2;
    otherwise
        fftset.jw = 1;
end
%
%% Spectral analyser
spectrum = zeros(size(freq, 1), size(xs, 2));
%
for i = 1:size(xs, 2)
    % Preallocate an array for temporary spectra
    spectra = zeros(size(freq, 1), imax);
    % Frequency analysis of individual segments
    for j = 1:imax
        % Fast Fourier transformation of the weighted segment
        fftSamp = fft(fftset.window .* xs(ind(j,1):ind(j,2), i), ...
                      fftset.nwin) / fftset.nwin;
        % Application of the jw weigthing and the low-pass filtering
        spectra(:, j) = fftset.jw .* fftSamp(1:size(freq, 1));
        % Evaluation of spectral unit
        switch lower(fftset.unit)
            case 'rms'           % Linear spectrum with rms magnitude
                spectra(2:end-sh,j) = (2/sqrt(2))*abs(spectra(2:end-sh,j));
                spectra(end-sh+1:end,j) = abs(spectra(end-sh+1:end,j))/sqrt(2);
            case 'pk'            % Linear spectrum with 0-peak magnitude
                spectra(2:end-sh,j) = 2 * abs(spectra(2:end-sh,j));
            case 'pp'            % Linear spectrum with peak-peak magnitude
                spectra(2:end-sh,j) = 4 * abs(spectra(2:end-sh,j));
                spectra(end-sh+1:end,j) = 2 * abs(spectra(end-sh+1:end,j));
            case 'psd'           % Power spectral density
                spectra(2:end-sh,j) = sqrt(2) * spectra(2:end-sh,j);
                spectra(:,j)        = (1 / fftset.noiseband) * spectra(:,j) ...
                                       .* conj(spectra(:,j));
            case {'rsd','rmspsd'}% Root mean square of PSD 
                spectra(2:end-sh,j) = sqrt(2) * spectra(2:end-sh,j);
                spectra(:,j)        = sqrt((1 / fftset.noiseband) * ...
                                       spectra(:,j) .* conj(spectra(:,j)));                
            otherwise            % Autospectrum
                spectra(2:end-sh,j) = sqrt(2) * spectra(2:end-sh,j);
                spectra(:,j)        = spectra(:,j) .* conj(spectra(:,j));
        end
    end
    % Spectral averaging
    switch lower(fftset.averaging)
        case {'energy', 'rms'}   % Energy averaging
            spectrum(:, i) = sqrt(sum(spectra.^2, 2) ./ imax);
        case {'max', 'peak'}     % Maximum peak hold averaging
            spectrum(:, i) = max(spectra, [], 2);
        case 'min'              % Minimum peak hold averaging
            spectrum(:, i) = min(spectra, [], 2);
        case 'none'             % No averaging
            if size(xs, 2) == 1
                spectrum = spectra;
            else
                spectrum{i} = spectra;
            end
        otherwise               % Linear averaging
            spectrum(:, i) = mean(spectra, 2);
    end
    % Remove imaginary part (residue due to spectra .* conj(spectra))
    spectrum = real(spectrum);
end
% End of main fucntion
end
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% Subfunction weightsig generates the time weighting window
%
% Input
%   - sym - symbol for the time weighting window
%   - n   - length of the time weighting window (samples)
%   - fs  - sampling frequency (Hz) 
%
% Output
%   - window    - the time weighting window
%   - noiseband - the noise power bandwidth of the time weighting window
%  
function [window, noiseband] = timeweight(sym, n, fs)
    % Generate the specified time weighting window
    switch sym(1)
        case 'b'    % Blackmann-Harris
            window = blackmanharris(n);
        case 'f'    % flat-top
            window = flattopwin(n);
        case 'h'    % Hann
            window = hann(n);
        case 'k'    % Kaiser-Bessel
            if length(sym) == 1
                % window with default beta = 0.5
                window = kaiser(n, 0.5);
            else
                % window with user specified beta
                window = kaiser(n, str2double(sym(2:end)));
            end
        case 'm'    % Hamming
            window = hamming(n);
        otherwise   % uniform
            window = rectwin(n);
    end
    % Adjust magnitude of the generated time weighting window
    window = window / mean(window);
    % Calculate the noise power bandwidth in Hz
    noiseband = enbw(window, fs);
end

تبدیل فوریه سریع در زبان C

با استفاده از برنامه زیر می‌توان تبدیل فوریه سریع را در زبان C محاسبه کرد.

/* 
 * Free FFT and convolution (C)
 *

#include <math.h>
#include <stddef.h>
#include <stdint.h>
#include <stdlib.h>
#include <string.h>
#include "fft.h"


// Private function prototypes
static size_t reverse_bits(size_t x, int n);
static void *memdup(const void *src, size_t n);


bool Fft_transform(double real[], double imag[], size_t n) {
	if (n == 0)
		return true;
	else if ((n & (n - 1)) == 0)  // Is power of 2
		return Fft_transformRadix2(real, imag, n);
	else  // More complicated algorithm for arbitrary sizes
		return Fft_transformBluestein(real, imag, n);
}


bool Fft_inverseTransform(double real[], double imag[], size_t n) {
	return Fft_transform(imag, real, n);
}


bool Fft_transformRadix2(double real[], double imag[], size_t n) {
	// Length variables
	bool status = false;
	int levels = 0;  // Compute levels = floor(log2(n))
	for (size_t temp = n; temp > 1U; temp >>= 1)
		levels++;
	if ((size_t)1U << levels != n)
		return false;  // n is not a power of 2
	
	// Trignometric tables
	if (SIZE_MAX / sizeof(double) < n / 2)
		return false;
	size_t size = (n / 2) * sizeof(double);
	double *cos_table = malloc(size);
	double *sin_table = malloc(size);
	if (cos_table == NULL || sin_table == NULL)
		goto cleanup;
	for (size_t i = 0; i < n / 2; i++) {
		cos_table[i] = cos(2 * M_PI * i / n);
		sin_table[i] = sin(2 * M_PI * i / n);
	}
	
	// Bit-reversed addressing permutation
	for (size_t i = 0; i < n; i++) {
		size_t j = reverse_bits(i, levels);
		if (j > i) {
			double temp = real[i];
			real[i] = real[j];
			real[j] = temp;
			temp = imag[i];
			imag[i] = imag[j];
			imag[j] = temp;
		}
	}
	
	// Cooley-Tukey decimation-in-time radix-2 FFT
	for (size_t size = 2; size <= n; size *= 2) {
		size_t halfsize = size / 2;
		size_t tablestep = n / size;
		for (size_t i = 0; i < n; i += size) {
			for (size_t j = i, k = 0; j < i + halfsize; j++, k += tablestep) {
				size_t l = j + halfsize;
				double tpre =  real[l] * cos_table[k] + imag[l] * sin_table[k];
				double tpim = -real[l] * sin_table[k] + imag[l] * cos_table[k];
				real[l] = real[j] - tpre;
				imag[l] = imag[j] - tpim;
				real[j] += tpre;
				imag[j] += tpim;
			}
		}
		if (size == n)  // Prevent overflow in 'size *= 2'
			break;
	}
	status = true;
	
cleanup:
	free(cos_table);
	free(sin_table);
	return status;
}


bool Fft_transformBluestein(double real[], double imag[], size_t n) {
	bool status = false;
	
	// Find a power-of-2 convolution length m such that m >= n * 2 + 1
	size_t m = 1;
	while (m / 2 <= n) {
		if (m > SIZE_MAX / 2)
			return false;
		m *= 2;
	}
	
	// Allocate memory
	if (SIZE_MAX / sizeof(double) < n || SIZE_MAX / sizeof(double) < m)
		return false;
	size_t size_n = n * sizeof(double);
	size_t size_m = m * sizeof(double);
	double *cos_table = malloc(size_n);
	double *sin_table = malloc(size_n);
	double *areal = calloc(m, sizeof(double));
	double *aimag = calloc(m, sizeof(double));
	double *breal = calloc(m, sizeof(double));
	double *bimag = calloc(m, sizeof(double));
	double *creal = malloc(size_m);
	double *cimag = malloc(size_m);
	if (cos_table == NULL || sin_table == NULL
			|| areal == NULL || aimag == NULL
			|| breal == NULL || bimag == NULL
			|| creal == NULL || cimag == NULL)
		goto cleanup;
	
	// Trignometric tables
	for (size_t i = 0; i < n; i++) {
		unsigned long long temp = (unsigned long long)i * i;
		temp %= (unsigned long long)n * 2;
		double angle = M_PI * temp / n;
		cos_table[i] = cos(angle);
		sin_table[i] = sin(angle);
	}
	
	// Temporary vectors and preprocessing
	for (size_t i = 0; i < n; i++) {
		areal[i] =  real[i] * cos_table[i] + imag[i] * sin_table[i];
		aimag[i] = -real[i] * sin_table[i] + imag[i] * cos_table[i];
	}
	breal[0] = cos_table[0];
	bimag[0] = sin_table[0];
	for (size_t i = 1; i < n; i++) {
		breal[i] = breal[m - i] = cos_table[i];
		bimag[i] = bimag[m - i] = sin_table[i];
	}
	
	// Convolution
	if (!Fft_convolveComplex(areal, aimag, breal, bimag, creal, cimag, m))
		goto cleanup;
	
	// Postprocessing
	for (size_t i = 0; i < n; i++) {
		real[i] =  creal[i] * cos_table[i] + cimag[i] * sin_table[i];
		imag[i] = -creal[i] * sin_table[i] + cimag[i] * cos_table[i];
	}
	status = true;
	
	// Deallocation
cleanup:
	free(cimag);
	free(creal);
	free(bimag);
	free(breal);
	free(aimag);
	free(areal);
	free(sin_table);
	free(cos_table);
	return status;
}


bool Fft_convolveReal(const double x[], const double y[], double out[], size_t n) {
	bool status = false;
	double *ximag = calloc(n, sizeof(double));
	double *yimag = calloc(n, sizeof(double));
	double *zimag = calloc(n, sizeof(double));
	if (ximag == NULL || yimag == NULL || zimag == NULL)
		goto cleanup;
	
	status = Fft_convolveComplex(x, ximag, y, yimag, out, zimag, n);
cleanup:
	free(zimag);
	free(yimag);
	free(ximag);
	return status;
}


bool Fft_convolveComplex(
		const double xreal[], const double ximag[],
		const double yreal[], const double yimag[],
		double outreal[], double outimag[], size_t n) {
	
	bool status = false;
	if (SIZE_MAX / sizeof(double) < n)
		return false;
	size_t size = n * sizeof(double);
	
	double *xr = memdup(xreal, size);
	double *xi = memdup(ximag, size);
	double *yr = memdup(yreal, size);
	double *yi = memdup(yimag, size);
	if (xr == NULL || xi == NULL || yr == NULL || yi == NULL)
		goto cleanup;
	
	if (!Fft_transform(xr, xi, n))
		goto cleanup;
	if (!Fft_transform(yr, yi, n))
		goto cleanup;
	
	for (size_t i = 0; i < n; i++) {
		double temp = xr[i] * yr[i] - xi[i] * yi[i];
		xi[i] = xi[i] * yr[i] + xr[i] * yi[i];
		xr[i] = temp;
	}
	if (!Fft_inverseTransform(xr, xi, n))
		goto cleanup;
	
	for (size_t i = 0; i < n; i++) {  // Scaling (because this FFT implementation omits it)
		outreal[i] = xr[i] / n;
		outimag[i] = xi[i] / n;
	}
	status = true;
	
cleanup:
	free(yi);
	free(yr);
	free(xi);
	free(xr);
	return status;
}


static size_t reverse_bits(size_t x, int n) {
	size_t result = 0;
	for (int i = 0; i < n; i++, x >>= 1)
		result = (result << 1) | (x & 1U);
	return result;
}


static void *memdup(const void *src, size_t n) {
	void *dest = malloc(n);
	if (n > 0 && dest != NULL)
		memcpy(dest, src, n);
	return dest;
}

تبدیل فوریه سریع در زبان #C

با استفاده از کد زیر، می‌توان تبدیل فوریه سریع را با زبان #C پیاده‌سازی کرد.

/* 
 * Free FFT and convolution (C#)
 * 


using System;
using System.Numerics;


public sealed class Fft {
	
	/* 
	 * Computes the discrete Fourier transform (DFT) or inverse transform of the given complex vector, storing the result back into the vector.
	 * The vector can have any length. This is a wrapper function. The inverse transform does not perform scaling, so it is not a true inverse.
	 */
	public static void Transform(Complex[] vector, bool inverse) {
		int n = vector.Length;
		if (n == 0)
			return;
		else if ((n & (n - 1)) == 0)  // Is power of 2
			TransformRadix2(vector, inverse);
		else  // More complicated algorithm for arbitrary sizes
			TransformBluestein(vector, inverse);
	}
	
	
	/* 
	 * Computes the discrete Fourier transform (DFT) of the given complex vector, storing the result back into the vector.
	 * The vector's length must be a power of 2. Uses the Cooley-Tukey decimation-in-time radix-2 algorithm.
	 */
	public static void TransformRadix2(Complex[] vector, bool inverse) {
		// Length variables
		int n = vector.Length;
		int levels = 0;  // compute levels = floor(log2(n))
		for (int temp = n; temp > 1; temp >>= 1)
			levels++;
		if (1 << levels != n)
			throw new ArgumentException("Length is not a power of 2");
		
		// Trigonometric table
		Complex[] expTable = new Complex[n / 2];
		double coef = 2 * Math.PI / n * (inverse ? 1 : -1);
		for (int i = 0; i < n / 2; i++)
			expTable[i] = Complex.Exp(new Complex(0, i * coef));
		
		// Bit-reversed addressing permutation
		for (int i = 0; i < n; i++) {
			int j = (int)((uint)ReverseBits(i) >> (32 - levels));
			if (j > i) {
				Complex temp = vector[i];
				vector[i] = vector[j];
				vector[j] = temp;
			}
		}
		
		// Cooley-Tukey decimation-in-time radix-2 FFT
		for (int size = 2; size <= n; size *= 2) {
			int halfsize = size / 2;
			int tablestep = n / size;
			for (int i = 0; i < n; i += size) {
				for (int j = i, k = 0; j < i + halfsize; j++, k += tablestep) {
					Complex temp = vector[j + halfsize] * expTable[k];
					vector[j + halfsize] = vector[j] - temp;
					vector[j] += temp;
				}
			}
			if (size == n)  // Prevent overflow in 'size *= 2'
				break;
		}
	}
	
	
	/* 
	 * Computes the discrete Fourier transform (DFT) of the given complex vector, storing the result back into the vector.
	 * The vector can have any length. This requires the convolution function, which in turn requires the radix-2 FFT function.
	 * Uses Bluestein's chirp z-transform algorithm.
	 */
	public static void TransformBluestein(Complex[] vector, bool inverse) {
		// Find a power-of-2 convolution length m such that m >= n * 2 + 1
		int n = vector.Length;
		if (n >= 0x20000000)
			throw new ArgumentException("Array too large");
		int m = 1;
		while (m < n * 2 + 1)
			m *= 2;
		
		// Trignometric table
		Complex[] expTable = new Complex[n];
		double coef = Math.PI / n * (inverse ? 1 : -1);
		for (int i = 0; i < n; i++) {
			int j = (int)((long)i * i % (n * 2));  // This is more accurate than j = i * i
			expTable[i] = Complex.Exp(new Complex(0, j * coef));
		}
		
		// Temporary vectors and preprocessing
		Complex[] avector = new Complex[m];
		for (int i = 0; i < n; i++)
			avector[i] = vector[i] * expTable[i];
		Complex[] bvector = new Complex[m];
		bvector[0] = expTable[0];
		for (int i = 1; i < n; i++)
			bvector[i] = bvector[m - i] = Complex.Conjugate(expTable[i]);
		
		// Convolution
		Complex[] cvector = new Complex[m];
		Convolve(avector, bvector, cvector);
		
		// Postprocessing
		for (int i = 0; i < n; i++)
			vector[i] = cvector[i] * expTable[i];
	}
	
	
	/* 
	 * Computes the circular convolution of the given complex vectors. Each vector's length must be the same.
	 */
	public static void Convolve(Complex[] xvector, Complex[] yvector, Complex[] outvector) {
		int n = xvector.Length;
		if (n != yvector.Length || n != outvector.Length)
			throw new ArgumentException("Mismatched lengths");
		xvector = (Complex[])xvector.Clone();
		yvector = (Complex[])yvector.Clone();
		Transform(xvector, false);
		Transform(yvector, false);
		for (int i = 0; i < n; i++)
			xvector[i] *= yvector[i];
		Transform(xvector, true);
		for (int i = 0; i < n; i++)  // Scaling (because this FFT implementation omits it)
			outvector[i] = xvector[i] / n;
	}
	
	
	private static int ReverseBits(int val) {
		int result = 0;
		for (int i = 0; i < 32; i++, val >>= 1)
			result = (result << 1) | (val & 1);
		return result;
	}
	
}

تبدیل فوریه سریع در زبان جاوا اسکریپت

جهت دسترسی به کدهای پیاده‌سازی تبدیل فوریه سریع یا fft در جاوا اسکریپت، روی این لینک کلیک کنید و فایل مربوطه حاوی کدهای جاوا اسکریپت را دریافت کنید.

اگر مطلب بالا برای شما مفید بوده و علاقه‌مند به موضوعات مرتبط با آن‌ هستید، پیشنهاد می‌کنیم آموزش‌های زیر را نیز ببینید:

• مجموعه آموزش‌های پردازش سیگنال
• آموزش پردازش سیگنال‌های دیجیتال با متلب
• مجموعه آموزش‌‌های مهندسی الکترونیک
• آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎
• تبدیل موجک — از صفر تا صد
• سری فوریه مختلط — به زبان ساده
• شبکه عصبی در متلب — از صفر تا صد

^^