الگوریتم *A — به زبان ساده

در این مطلب، «الگوریتم *A» به طور جامع و همراه با مثال مورد بررسی قرار گرفته و پیادهسازی آن در زبانهای برنامهنویسی گوناگون شامل ++C، «پایتون» (Python Programming Language) و «جاوا» (Java Programming Language) انجام شده است. در علوم کامپیوتر، الگوریتم *A (تلفظ آن، A Star است)، الگوریتمی است که به طور گسترده برای «مسیریابی» (Pathfinding) و «پیمایش گراف» (Graph Traversal) مورد استفاده قرار میگیرد. پیمایش گراف، فرایند پیدا کردن مسیر بین نقاط گوناگونی است که به آنها «گره» (Node) گفته میشود. الگوریتم *A به دلیل کارایی و صحتی که دارد، به طور گسترده در کاربردهای گوناگون مورد استفاده قرار میگیرد. البته، در سیستمهای عملی مسیریابی سفر، معمولا بهتر است از الگوریتمهایی استفاده شود که میتوانند گراف را برای حصول کارایی بهتر، «پیشپردازش» (Preprocess) کنند. هر چند بر اساس برخی از پژوهشهای انجام شده، در این سیستمها نیز الگوریتم *A نسبت به دیگر رویکردها، دارای عملکرد بهتری است.
«پیتر هارت» (Peter Hart)، «نیلز نیلسون» (Nils Nilsson) و «برترام رافائل» (Bertram Raphael) از «موسسه پژوهشی استنفورد» (Stanford Research Institute) که اکنون با عنوان «اسآرآی اینترنشنال» (SRI International) فعالیت میکند، برای اولینبار، مقالهای پیرامون الگوریتم *A را در سال ۱۹۶۳ منتشر کردند. این الگوریتم را میتوان به عنوان افزونهای از «الگوریتم دیکسترا» (Dijkstra's Algorithm) در نظر گرفت که توسط «ادسخر دیکسترا» (Edsger Dijkstra) در سال ۱۹۵۹ ارائه شده است. الگوریتم *A با بهرهگیری از «الگوریتم جستجوی کاشف» (جستجوی هیوریستیک | Heuristics Search) برای هدایت فرایند جستجو، به کارایی بهتری دست پیدا میکند.
الگوریتم *A در یک نگاه
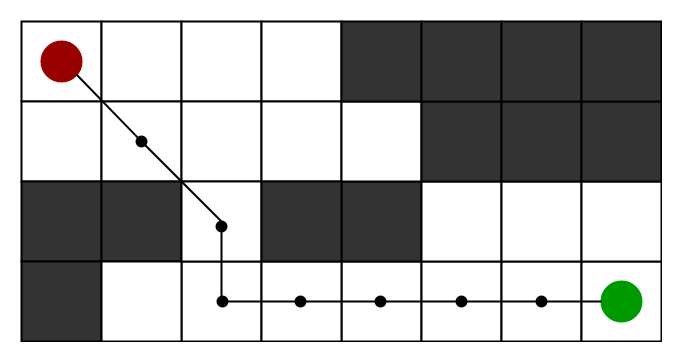
از الگوریتم *A برای تخمین کوتاهترین مسیر در مسائل جهان واقعی مانند نقشهها و بازیهایی که امکان دارد موانع زیادی در آنها باشد، استفاده میشود. میتوان یک شبکه 2D را در نظر گرفت که دارای چندین مانع است؛ کار جستجو در این شبکه، از سلول منبع (به رنگ قرمز رنگآمیزی شده است) برای رسیدن به سلول هدف آغاز میشود (به رنگ سبز، رنگآمیزی شده است).
الگوریتم جستجوی *A یکی از بهترین و محبوبترین روشهای مورد استفاده در مسیریابی و پیمایش گراف است.
چرا الگوریتم جستجوی *A
الگوریتم *A برخلاف دیگر روشهای پیمایش گراف، دارای «مغز» است. این یعنی، *A الگوریتم بسیار هوشمندی است و همین ویژگی، موجب تمایز آن از دیگر الگوریتمهای مرسوم میشود. این موضوع، همراه با جزئیات بیشتر در ادامه تشریح میشود. شایان ذکر است که بسیاری از بازیها و نقشههای مبتنی بر وب، از الگوریتم *A برای پیدا کردن کوتاهترین مسیر به طور کاملا موثر، استفاده میکنند.
روش کار الگوریتم *A
یک شبکه مربعی که موانع زیادی در آن وجود دارد مفروض است. همچنین، یک خانه به عنوان خانه شروع و یک خانه به عنوان خانه مقصد (هدف) در نظر گرفته میشود. کاربر میخواهد (در صورت امکان) از خانه شروع آغاز به کار کند و با سریعترین حالت ممکن به خانه مقصد برسد. در اینجا، الگوریتم جستجوی *A نقشآفرین میشود.
کاری که الگوریتم *A انجام میدهد آن است که در هر گام، گره را متناسب با مقدار «f» که پارامتری مساوی با مجموع دو پارامتر دیگر g و h است انتخاب میکند. در هر گام، گره/خانهای که دارای کمترین مقدار f است را انتخاب و آن گره/خانه را پردازش میکند. g و h به روش سادهای که در زیر بیان شده است محاسبه میشوند.
g: هزینه حرکت از نقطه آغاز به یک مربع خاص در شبکه، با دنبال کردن مسیری که برای رسیدن به آن تولید شده است.
h: هزینه تخمین زده شده برای حرکت از یک خانه داده شده در شبکه به مقصد نهایی است. از h معمولا با عنوان هیوریستیک یاد میشود. هیوریستیک چیزی به جز نوعی حدس هوشمندانه نیست. کاربر واقعا فاصله واقعی را تا هنگام یافتن مسیر نمیداند، زیرا هر مانعی (دیوار، آب و سایر موانع) ممکن است در مسیر باشد. راههای زیادی برای محاسبه h وجود دارد که در ادامه به آنها اشاره شده است.
الگوریتم *A
ابتدا باید دو لیست «Open List» و «Closed List» ساخته شوند. این مورد، مشابه با کاری است که در الگوریتم دیکسترا انجام میشود. شایان توجه است که در این متن، «گره بعدی» معادلی برای واژه «Successor» است.
//الگوریتم جستجوی *A
- Open List را مقداردهی اولیه کن.
- Closed List را مقداردهی اولیه کن.
- گره آغازین را در Open List قرار بده (میتوان f آن را برابر با صفر قرار داد).
- تا هنگامی که open list خالی نیست:
- گرهای با کمترین f را در open list قرار بده و آن را «q» نامگذاری کن.
- q را از open list خارج کن.
- هشت گره بعدی (رو به جلو) را تولید کن و q را والد آنها قرار بده.
- برای هر گره بعدی:
- اگر گره بعدی هدف است، جستجو را متوقف کن.
- گره بعدی × g = فاصله بین q و گره بعدی + q.g
- گره بعدی × h = فاصله از هدف تا گره بعدی (این کار با استفاده از راهکارهای زیادی قابل انجام است؛ از هیوریستیک منهتن، قطری و اقلیدسی میتوان برای این کار استفاده کرد.)
- گره بعدی × f = گرهبعدی × g + گره بعدی × h
- اگر یک گره با موقعیت مشابه به عنوان گره بعدی در OPEN list قرار دارد و دارای f کمتر از گره بعدی است، از این گره بعدی صرف نظر کن.
- اگر یک گره با موقعیت مشابه با والد، در CLOSED list قرار دارد و دارای f کمتر از گره بعدی است، از این گره بعدی صرف نظر کن. در غیر این صورت، گره را به open list اضافه کن.
- پایان (حلقه for)
- q را در CLOSED list قرار بده (حلقه while).
به عنوان مثال اگر هدف، رسیدن به سلول هدف از سلول منبع باشد، الگوریتم جستجوی *A مسیری مانند آنچه در زیر آمده است را طی میکند. شایان توجه است که تصویر زیر، با استفاده از هیوریستیک فاصله اقلیدسی ساخته شده است.
هیوریستیک
میتوان g را محاسبه کرد؛ اما چطور باید h را محاسبه کرد؟ در این راستا، میتوان اقدامات زیر را انجام داد.
- محاسبه مقدار دقیق h (که قطعا زمانبر است)
یا
- تخمین مقدار h با استفاده از برخی از هیوریستیکها (کمتر زمانبر است)
هر دو روش بالا، در ادامه بیشتر تشریح میشوند.
هیوریستیک دقیق
میتوان مقدار دقیق h را پیدا کرد، اما این کار بسیار زمانبر است. در ادامه، روشهایی برای محاسبه مقدار دقیق h بیان شده است.
- پیشمحاسبه فاصله بین هر جفت از سلولها، پیش از اجرای الگوریتم جستجوی *A.
- اگر هیچ سلول مسدود شدهای (دارای مانع) وجود نداشته باشد، میتواند مقدار دقیق h را بدون هر گونه پیشمحاسبهای با استفاده از «فاصله اقلیدسی» (Euclidean Distance) محاسبه کرد.
هیوریستیکهای تخمین
به طور کلی، سه هیوریستیک تخمین برای محاسبه h وجود دارد که در ادامه بیان شدهاند.
فاصله منهتن
«فاصله منهتن» (Manhattan Distance) در واقع قدر مطلق تفاضل مختصات x خانه هدف از مختصات x خانه کنونی و مختصات y خانه هدف از y خانه کنونی است.
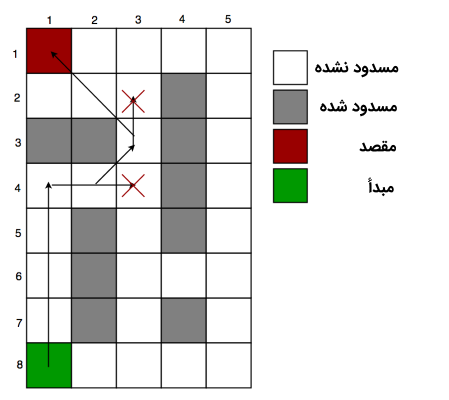
پرسشی که در این وهله مطرح میشود آن است که چه هنگامی میتوان از این هیوریستیک استفاده کرد؟ پاسخ این پرسش آن است که وقتی میتوان از فاصله منهتن استفاده کرد که حرکت تنها در چهار جهت (راست، چپ، بالا و پایین) پذیرفته شده باشد. هیوریستیک فاصله منهتن در تصویر زیر نمایش داده شده است (نقطه قرمز به عنوان خانه مبدا و نقطه سبز به خانه عنوان مقصد در نظر گرفته شده است).

فاصله قطری
«فاصله قطری» (Diagonal Distance) در واقع بیشینه مقادیر قدر مطلق تفاضل مختصات x خانه هدف از مختصات x خانه کنونی و مختصات y خانه هدف از y خانه کنونی است.
در پاسخ به این پرسش که چه زمان میتوان از این هیوریستیک استفاده کرد باید گفت، هنگامی که امکان حرکت در هشت جهت وجود دارد (مانند شاه در شطرنج). هیوریستیک فاصله قطری در تصویر زیر نشان داده شده است (نقطه قرمز به عنوان خانه مبدا و نقطه سبز به عنوان خانه مقصد در نظر گرفته شده است).

فاصله اقلیدسی
همانطور که از نام این هیوریستیک مشخص است، «فاصله اقلیدسی» (Euclidean Distance) در واقع فاصله بین خانه کنونی و خانه هدف با استفاده از فرمول فاصله است.
پرسشی که در این وهله مطرح میشود آن است که این هیوریستیک چه هنگامی قابل استفاده است؟ در پاسخ به این پرسش باید گفت که این هیوریستیک هنگامی قابل استفاده است که امکان حرکت در هر جهتی وجود داشته باشد. هیوریستیک فاصله اقلیدسی در تصویر زیر نمایش داده شده است (نقطه قرمز به عنوان خانه مبدا و نقطه سبز به عنوان خانه مقصد در نظر گرفته شده است).
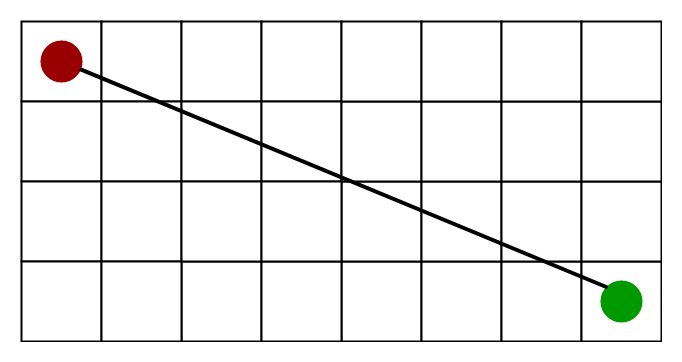
باید توجه داشت همانطور که پیش از این نیز بیان شد، الگوریتم دیکسترا حالت خاصی از الگوریتم *A است که در آن، برای همه گرهها h = 0 است.
تاریخچه الگوریتم *A
الگوریتم *A به عنوان بخشی از پروژه «Shakey The Robot» که هدف آن ساخت یک ربات موبایل بود که میتوانست فعالیتهای خودش را برنامهریزی کند، ساخته شد. نیلز نیلسون، در اصل «الگوریتم پیمایش گراف» (Graph Traversal Algorithm) را برای برنامهریزی مسیر Shakey ارائه کرد. پیمایش گراف در الگوریتم Graph Traverser به وسیله تابع هیوریستیک (h(n، فاصله تخمین زده شده از n تا گره هدف، هدایت میشد و به طور کلی (g(n را که فاصله از گره آغازین (مبدا) به گره n بود نادیده میگرفت.
بترام رافائل پیشنهاد داد تا از مجموع (g(n) + h(n استفاده شود. پیتر هارت مفاهیمی را ابداع کرد که امروزه به آنها «پذیرفتگی» (Admissibility) و «ثبات» (Consistency) تابع هیوریستیک گفته میشود. الگوریتم *A در اصل برای پیدا کردن مسیر با کمترین هزینه طراحی شده بود که در آن، هزینه یک مسیر مجموع هزینه یالها بود؛ اما در ادامه ثابت شد که الگوریتم *A را میتوان برای پیدا کردن مسیر بهینه برای هر مسئلهای که شرایط جبر هزینه را محقق کند، استفاده کرد.
مقاله اصلی الگوریتم *A که در سال ۱۹۶۸ منتشر شد، حاوی نظریهای بود مبنی بر اینکه هیچ الگوریتم شبه *A نمیتواند گرههای کمتری را نسبت به الگوریتم *A گسترش دهد، اگر تابع هیوریستیک «ثابت» (Consistent) باشد و قاعده «رفع گرهخوردگی» (Tie-Breaking) به صورت مناسبی انتخاب شده باشد. اصلاحاتی چند سال بعد منتشر شد که نشان داد، نیاز به ثبات نیست و پذیرفتگی کافی است. اگرچه، چیزی که واقعا نشان میداد آن بود که هیچ الگوریتم مشابهی، با توجه به مجموعه گرههای توسعه یافته، نمیتواند اکیدا کارآمدتر از *A باشد.
چنانکه در پژوهشهای «دچتر» (Dechter) و «پیرل» (Pearl) پیرامون بهینگی (اکنون به آن کارایی بهینه گفته میشود) الگوریتم *A، نشان داده شده است که این امکان برای الگوریتمهای درست دیگر وجود دارد که در برخی گرافها کارایی بهتری نسبت به الگوریتم *A داشته باشند؛ در حالیکه در برخی از دیگر گرافها و یا برای گسترش گرههایی که حاوی مجموعه گرههای گسترش یافته با *A است و یا گرههایی در آن قرار دارند ، نتیجه را به *A واگذار میکنند و در واقع الگوریتم *A عملکرد بهتری دارد.
الگوریتم *A از جمله «الگوریتمهای جستجوی آگاهانه» (Informed Search Algorithm) یا «جستجوی اول بهترین» (Best-First Search) است؛ بدین معنا که برای گرافهای وزندار فرموله شده است. در این الگوریتم، با شروع از یک گره مشخص آغازین از گراف، هدف پیدا کردن مسیری به یک گره هدف داده شده است که کمترین هزینه را دارد (کمترین فاصله پیموده شده، کمترین زمان پیمایش و دیگر موارد). الگوریتم *A این کار را با نگهداری یک درخت از مسیرهایی که از گره آغازین (مبدا) نشأت میگیرند و گسترش دادن آن مسیرها به اندازه یک یال در هر زمان تا هنگامی که معیارهای توقف محقق شود، انجام میدهد. در هر تکرار از حلقه اصلی، الگوریتم *A نیاز به تعیین این دارد که کدام یک از مسیرها را باید گسترش بدهد. الگوریتم، این کار را بر اساس هزینه مسیر و یک تخمین از هزینه مورد نیاز برای گسترش مسیر از آن گره تا گره هدف انجام میدهد. به طور خاص، الگوریتم *A مسیری را انتخاب میکند که تابع زیر را کمینه میکند:
f(n) = g(n) + h(n)
در تابع بالا، n گره بعدی در مسیر، (g(n هزینه مسیر از مبدا تا گره n و (h(n تابع هیوریستیکی است که هزینه ارزانترین مسیر از گره n تا هدف را مشخص میکند. الگوریتم *A هنگامی متوقف میشود که مسیری که برای گسترش انتخاب کرده، مسیری باشد از مبدا تا هدف و یا هیچ گره مطلوب دیگری برای گسترش وجود نداشته باشد. انتخاب تابع هیوریستیک، مبتنی بر مسئله است. اگر تابع هیوریستیک پذیرفتنی باشد، بدین معنا که هزینه واقعی برای رسیدن به هدف را هیچگاه بیش از اندازه واقعی تخمین نمیزد، الگوریتم *A تضمین میکند که مسیری با کمترین هزینه از مبدا تا هدف (مقصد) را پیدا کند.
پیادهسازی متداول *A «از صف اولویتدار» (Priority Queue) برای انجام تکرار انتخاب (انتخاب تکرار شونده) استفاده و گرههای دارای کمترین هزینه (تخمین زده شده) جهت گسترش را انتخاب میکند. این صف اولویتدار، تحت عنوان «مجموعه باز» (Open Set) یا «فرینج» (Fringe) نامیده میشود. در هر گام از الگوریتم، گره دارای کمترین مقدار (f(x از صف حذف میشود، مقادیر f و g نیز متعاقبا از همسایههای آن به روز رسانی میشوند و این همسایهها، به صف اضافه میشوند. الگوریتم کار را تا جایی ادامه میدهد که گره هدف، دارای مقدار f کمتری نسبت به هر گره دیگری در صف باشد (یا تا هنگامی که صف خالی است). مقدار f هدف، هزینه کوتاهترین مسیر است، زیرا h در هدف، در یک هیوریستیک پذیرفتنی، برابر با صفر است.
الگوریتمی که تاکنون تشریح شده است، فقط طول کوتاهترین مسیر را به دست میدهد. برای پیدا کردن توالی واقعی گامها، الگوریتم میتواند به سادگی معکوس شود، بنابراین هر گره اجداد خود را دنبال میکند. پس از اینکه این الگوریتم اجرا شد، گره پایانی (مقصد) به اجداد خود اشاره میکند و به همین ترتیب، تا رسیدن اجداد گرهها به گره آغازین (مبدا)، کار ادامه پیدا میکند. به عنوان مثال، هنگام جستجو برای کوتاهترین مسیر روی یک نقشه، (h(x ممکن است فاصله خط مستقیم از هدف را نشان دهد؛ زیرا به لحاظ فیزیکی، کمترین فاصله بین دو نقطه است. اگر هیوریستیک h شرط اضافی (h(x) ≤ d(x, y) + h(y را برای هر یال (x, y) در گراف محقق کند (که در آن، d نشانگر طول یال است)، h را «یکنواخت» (Monotone) یا «ثابت» (Consistent) گویند. در این شرایط، *A را میتوان به صورت کارآمدتری پیادهسازی کرد؛ در واقع، هیچ گرهای نیاز به پیادهسازی بیش از یکبار ندارد و الگوریتم *A برابر با اجرای الگوریتم دیکسترا با هزینه کاهش یافته (d'(x, y) = d(x, y) + h(y) − h(x است.
شبه کد الگوریتم *A
شبه کد الگوریتم دیکسترا، در ادامه آمده است.
1function reconstruct_path(cameFrom, current)
2 total_path := {current}
3 while current in cameFrom.Keys:
4 current := cameFrom[current]
5 total_path.append(current)
6 return total_path
7
8function A_Star(start, goal)
9 // The set of nodes already evaluated
10 closedSet := {}
11
12 // The set of currently discovered nodes that are not evaluated yet.
13 // Initially, only the start node is known.
14 openSet := {start}
15
16 // For each node, which node it can most efficiently be reached from.
17 // If a node can be reached from many nodes, cameFrom will eventually contain the
18 // most efficient previous step.
19 cameFrom := an empty map
20
21 // For each node, the cost of getting from the start node to that node.
22 gScore := map with default value of Infinity
23
24 // The cost of going from start to start is zero.
25 gScore[start] := 0
26
27 // For each node, the total cost of getting from the start node to the goal
28 // by passing by that node. That value is partly known, partly heuristic.
29 fScore := map with default value of Infinity
30
31 // For the first node, that value is completely heuristic.
32 fScore[start] := heuristic_cost_estimate(start, goal)
33
34 while openSet is not empty
35 current := the node in openSet having the lowest fScore[] value
36 if current = goal
37 return reconstruct_path(cameFrom, current)
38
39 openSet.Remove(current)
40 closedSet.Add(current)
41
42 for each neighbor of current
43 if neighbor in closedSet
44 continue // Ignore the neighbor which is already evaluated.
45
46 // The distance from start to a neighbor
47 tentative_gScore := gScore[current] + dist_between(current, neighbor)
48
49 if neighbor not in openSet // Discover a new node
50 openSet.Add(neighbor)
51 else if tentative_gScore >= gScore[neighbor]
52 continue
53
54 // This path is the best until now. Record it!
55 cameFrom[neighbor] := current
56 gScore[neighbor] := tentative_gScore
57 fScore[neighbor] := gScore[neighbor] + heuristic_cost_estimate(neighbor, goal)شایان توجه است که در شبه کد بالا اگر به یک گره از یک مسیر رسیده شد، از openSet حذف شده و متعاقبا به وسیله مسیر کم هزینهتری به آن رسیده شود، مجددا به openSet اضافه میشود. این مورد برای تضمین آنکه مسیر بازگردانده شده بهینه است اگر تابع هیوریستیک پذیرفتنی و نه ثابت است، امری حیاتی محسوب میشود. اگر هیوریستیک ثابت باشد، هنگامی که یک گره از openSet حذف میشود، تضمین میشود که مسیر به آن گره بهینه است، بنابراین «tentative_gScore < gScore[neighbor]» همواره در صورتی که مجددا به گره رسیده شود، با شکست مواجه خواهد شد.
مثالی از الگوریتم *A
مثالی از حل یک مسئله با الگوریتم *A در ادامه ارائه شده است. در گراف زیر، شهرها به صورت راسهایی هستند که با یالها (راهها) به یکدیگر متصل شدهاند.
(h(x فاصله خط راست از نقطه هدف است.
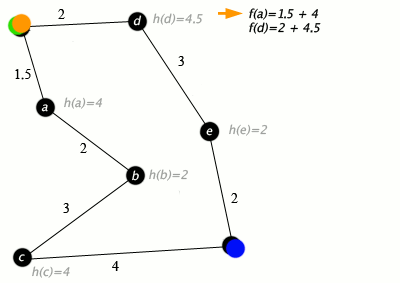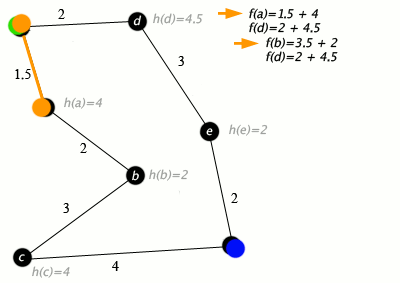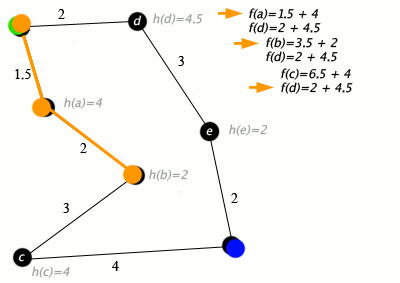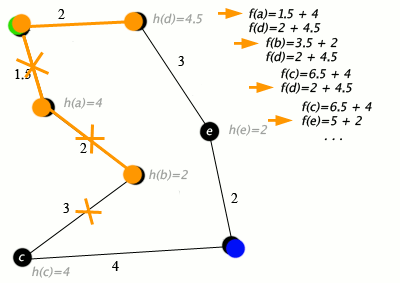
در گراف بالا، راس سبز رنگ، نقطه شروع یا مبدا، و راس آبی، هدف یا همان مقصد است. موارد نارنجی نیز راسها و یالهای ملاقات شده هستند. الگوریتم *A کاربردهای جهان واقعی نیز دارد. در این مثال، یالها جادههای ریلی و (h(x فاصله دایره بزرگ (کوتاهترین مسیر ممکن روی کره) از هدف است. الگوریتم در صدد یافتن مسیر بین «واشینگتون دی.سی» (Washington, D.C) و «لس آنجلس» (Los Angeles) است.
حالات خاص الگوریتم *A
الگوریتم دیکسترا، مثال دیگری از الگوریتم جستجوی دارای هزینه یکنواخت (Uniform-Cost) است که میتوان آن را به عنوان گونه خاصی از *A در نظر گرفت که در آن برای همه xها ۰ = (h(x است. الگوریتم «جستجوی اول عمق» (Depth-First Search) عمومی را میتوان با استفاده از *A و با در نظر داشتن اینکه یک شمارنده سراسری C با یک مقدار بسیار بزرگ مقداردهی اولیه شده است، پیادهسازی کرد.
پس از هر بار تخصیص، شمارنده C یک واحد کاهش داده میشود. بنابراین، هر چه زودتر یک گره کشف شود، مقدار (h(x آن بالاتر خواهد بود. هم الگوریتم دیکسترا و هم جستجوی اول عمق را میتوان به صورت کاراتر بدون در نظر گرفتن (h(x در هر گره، پیادهسازی کرد.
جزئیات پیادهسازی الگوریتم *A
بهینهسازیهای ساده یا جزئیات بهینهسازی وجود دارد که میتواند به طور موثر کارایی پیادهسازی الگوریتم *A را تحت تاثیر قرار دهد. اولین جزئیاتی که باید به آن دقت کرد، روشی است که صف اولویت گرههای (Ties) صف را مدیریت میکند؛ این موضوع در برخی شرایط، تاثیر قابل توجهی روی کارایی دارد. اگر گرهها (Ties) شکسته شده باشند، صف با حالت LIFO خودش عمل خواهد کرد و در نتیجه، *A مانند جستجوی اول عمق در میان مسیرهایی با هزینه یکسان رفتار میکند (اجتناب از اکتشاف بیش از یک راهکار با بهینگی مشابه).
هنگامی که یک مسیر در پایان جستجو مورد نیاز باشد، متداول است که با هر گره یک ارجاع به والد آن گره نگهداری شود. در پایان جستجو، این مراجع را میتوان برای یافتن مسیر بهینه استفاده کرد. اگر این مراجع نگهداری شوند، حائز اهمیت است که گره مشابه در صف اولویت بیش از یک بار ظاهر نشود (هر ورودی مربوط به مسیر متفاوتی به گره و هر کدام با هزینه متفاوتی).
یک راهکار استاندارد بررسی این است که یک گره افزوده شده، در صف اولویت ظاهر شود. اگر چنین باشد، اشارهگرهای اولویت و والد برای مربوط شدن به مسیر دارای هزینه کمتر، تغییر پیدا میکنند. یک «هرم دودویی» (Binary Heap) استاندارد، بر مبنای صف اولویت به طور مستقیم عملیات جستجو برای یکی از عناصر آن را پشتیبانی نمیکند، اما میتواند با «جدول هش» که عناصر را به جایگاه خودشان در هرم نگاشت میکنند تکمیل (تجمیع) شود، که این امکان را فراهم میکند که عملیات کاهش اولویت در زمان لگاریتمی انجام شود. به طور جایگزین، یک هرم فیبوناچی میتواند عملیات کاهش اولویت مشابهی را در زمان استهلاکی ثابتی انجام دهد.
پذیرش و بهینگی
الگوریتم *A پذیرفتنی است و در برخی شرایط، گرههای کمتری را نسبت به دیگر الگوریتمهای جستجوی پذیرفتنی با هیوریستیک مشابه در نظر میگیرد. این امر به دلیل آن است که *A از یک تخمین «خوشبینانه» هزینه مسیر از هر گره، استفاده میکند که خوشبینانه در نظر میگیرد که هزینه واقعی مسیر از یک گره به هدف دستکم به بزرگی تخمین زده شده است. اما، با نگاهی منتقدانه میتوان گفت تخمین بهینه فقط همانقدر که *A «فکر میکند» قابل دستیابی است. برای اثبات پذیرفتنی بودن *A، مسیر راهکار بازگردانده شده توسط الگوریتم، به صورت زیر مورد استفاده قرار میگیرد.
هنگامی که *A به جستجوی خود پایان میدهد، مسیری را یافته که هزینه آن از هزینه تخمین زده شده برای هر مسیر دیگر از طریق هر گره بازی، کمتر است. اما با توجه به اینکه این تخمینها بهینه هستند، *A میتواند با امنیت آن گرهها را نادیده انگارد. به بیان دیگر، *A هرگز احتمال مسیر با هزینه کمتر را نادیده نمیگیرد و بنابراین، پذیرفتنی است.
اکنون، فرض میشود که یک الگوریتم هیوریستیک دیگر B جستجوی خود را با مسیری که هزینه واقعی آن کمتر از هزینه تخمین زده شده از طریق گرههای باز است، متوقف میکند. بر مبنای اطلاعات هیوریستیکی که B دارد، الگوریتم B نمیتواند احتمال اینکه مسیر از طریق آن گرهها دارای کمترین هزینه است را غیر محتمل بشمارد. بنابراین، در حالی که B ممکن است گرههای کمتری را نسبت به *A در نظر بگیرد، پذیرفتنی نیست. بر این اساس، *A کمترین گرهها را نسبت به هر الگوریتم جستجوی پذیرفتنی دیگری، در نظر میگیرد. این موضوع تنها هنگامی درست است که:
- *A از یک هیوریستیک پذیرفتنی استفاده کند. در غیر این صورت، *A تضمین نمیکند که گرههای کمتری را نسبت به دیگر الگوریتمها با هیوریستیک مشابه، گسترش دهد.
- *A تنها یک مسئله جستجو را به جای مجموعهای از مسائل جستجوی مشابه، حل میکند. در غیر این صورت، *A تضمین نمیکند که گرههای کمتری را نسبت به الگوریتمهای جستجوی هیوریستیک افزایشی گسترش دهد.
آزادسازی محدود (Bounded Relaxation)
در حالی که معیار پذیرفتنی یک مسیر راهکار بهینه را تضمین میکند، بدین معنا است که *A باید همه مسیرهایی که به طور مشابه شایسته انتخاب مسیر بهینه هستند را مورد آزمون قرار دهد. برای محاسبه تقریب کوتاهترین مسیر، این امکان وجود دارد که جستجو را در هزینه بهینهسازی با آزادسازی معیار پذیرش سرعت ببخشد.
گاهی، کاربر تمایل دارد که این آزادسازی را محدود کند، بنابراین میتواند تضمین کند که مسیر راهکار بیش از (1 + ε) برابر مسیر راهکار بهینه بدتر نیست. این تضمین جدید، با عنوان ε-پذیرفتنی (ε-admissible) نامیده میشود. تعدادی الگوریتم ε-پذیرفتنی وجود دارند که در ادامه معرفی شدهاند.
- *A وزندار/وزندهی ایستا (Weighted A*/Static Weighting): اگر (ha(n یک تابع هیوریستیک پذیرفتنی باشد، در نسخه وزندار جستجوی *A از hw(n) = ε ha(n), ε > 1 به عنوان تابع هیوریستیک استفاده میشود و جستجوی *A به طور متداول (که در نهایت سریعتر از استفاده از ha به وقوع میپیوندد، زیرا گرههای کمتری گسترش پیدا کردهاند) انجام میشود. بدین ترتیب، مسیر یافته شده توسط الگوریتم جستجو میتواند هزینهای حداکثر ε برابر مسیر با کمترین هزینه در گراف را داشته باشد.
- وزندهی پویا (Dynamic Weighting): از تابع هزینه (f(n) = g(n) + (1+εw(n))h(n استفاده میکند که در آن ، که (d(n عمق جستجو و N طول پیشبینی شده مسیر راهکار است.
- وزندهی پویای نمونهگیری شده (Sampled Dynamic Weighting): از نمونهگیری از گرهها برای تخمین بهتر و رفع سوگیری خطای هیوریستیک استفاده میکند.
- : از دو تابع هیوریستیک استفاده میکند. اولین تابع، لیست FOCAL است که برای انتخاب گرههای کاندید مورد استفاده قرار میگیرد و دومین مورد، hF برای انتخاب امیدوارکنندهترین گره از لیست FOCAL به کار میرود.
- : گرهها را با تابع Af(n)+Bh_{f}(n) انتخاب میکند که در آنها A و B ثابتها هستند. اگر هیچ گرهای قابل انتخاب نباشد، الگوریتم با تابع پسگرد میکند که در آن، C و D ثابتها هستند.
- *AlphA: برای ارتقای استخراج اول عمق با ترجیح دادن گرههایی که اخیرا گسترش یافتهاند تلاش میکند. *AlphA از تابع هزینه استفاده میکند که در آن، ، که در این رابطه λ و Λ مقادیر ثابت با است و والد n و گره اخیرا گسترش یافته است.
پیچیدگی
پیچیدگی زمانی الگوریتم *A بستگی به هیوریستیک دارد. در بدترین حالت از فضای جستجوی نامحدود، تعداد گرهها به صورت نمایی در عمق راهکار گسترش یافتهاند (کوتاهترین مسیر) (d: O(bd که در آن، b ضریب انشعاب است. در اینجا فرض میشود که حالت هدف وجود دارد و از حالت ابتدایی دسترسیپذیر است. در غیر این صورت، و در حالتی که فضای حالت نامتناهی باشد، الگوریتم متوقف نمیشود.
تابع هیوریستیک، دارای یک اثر کلی در کارایی عملی الگوریتم *A است، زیرا یک هیوریستیک خوب این امکان را فراهم میکند که *A بسیاری از گرههای bd را که جستجوی ناآگاهانه گسترش میدهد، هرس کند. کیفیت این الگوریتم را میتوان با استفاده از ضریب انشعاب موثر *b سنجید که میتواند به صورت تجربی برای یک نمونه مساله با اندازهگیری تعداد گرههای گسترش یافته، N و عمق راهکار و سپس حل معادله زیر تعیین کرد.
N + 1 = 1 + b* + (b*)2+...+(b*)d
هیوریستیکهای خوب، مواردی هستند که دارای ضریب انشعاب کمتری هستند (بهینگی با b* = 1). هنگامی که فضای جستجو یک درخت است، یک حالت هدف وجود دارد، تابع هیوریستیک h شرایط معادله زیر را برآورده میکند و پیچیدگی زمانی چندجملهای خواهد بود.
|h(x) - H*(x)| = O(log h*(x))
که در آن *h یک هیوریستیک بهینه و هزینه دقیق رسیدن از x به هدف است. به عبارت دیگر، خطای h سریعتر از لگاریتم «هیوریستیک کامل» (Perfect Heuristic) یعنی *h که مقدار صحیح فاصله x از هدف را باز میگرداند، رشد نخواهد کرد.
کاربردها
الگوریتم *A به طور متداول برای مسائل مسیریابی در مواردی مانند بازیها مورد استفاد میگیرد، اما در اصل، برای الگوریتم پیمایش کلی گراف طراحی شده بود. این الگوریتم، کاربردهایی در مسائل گوناگون دارد که از این جمله میتوان به مساله «تجزیه کننده» (Parsing) با استفاده از «گرامر تصادفی» (Stochastic Grammars) در «پردازش زبان طبیعی» (Natural Language Processing) اشاره کرد. دیگر موارد شامل «جستجوی اطلاعاتی» (Informational Search) با «یادگیری آنلاین» (Online Learning) میشوند.
ارتباط با دیگر الگوریتمها
آنچه الگوریتم *A را از «الگوریتم حریصانه جستجوی اول بهترین» (Greedy Best-First Search Algorithm) متمایز میکند، این است که این الگوریتم هزینهای/فاصلهای که تاکنون پیموده شده است، یعنی (g(n را در محاسبات خود دخیل میکند.
گونههای متداولی از الگوریتم دیکسترا وجود دارند که میتوان به آنها به عنوان نوع خاصی از الگوریتم *A نگاه کرد و در آنها، برای همه گرهها داریم که هیوریستیک 0 = (h(n است. هر دو الگوریتم دیکسترا و *A به نوبه خود، گونه خاصی از «برنامهنویسی پویا» (Dynamic Programming) محسوب میشوند. *A خود، گونه خاصی از تعمیم الگوریتم «شاخه و حد» (Branch and Bound) است و میتواند از الگوریتم اولیه-دوگان (Primal-Dual Algorithm) برای «برنامهنویسی خطی» (Linear Programming) مشتق شود.
گونههای الگوریتم *A
الگوریتم *A گونههای مختلفی دارد که عناوین برخی از آنها در ادامه بیان شدهاند.
- جستجوی هیوریستیک افزایش (Incremental heuristic search)
- *A اصلاح در هر زمان (*Anytime Repairing A* | ARA)
- *A مسدود
- *D
- *D زمینه
- فرینج (Fringe)
- فرینج سیوینگ *A (به اختصار *Fringe Saving A*| FSA)
- *A تعمیم یافته تطبیقپذیر (*Generalized Adaptive A* | GAA)
- *A تکرار شونده عمیقتر
- جستجوی اطلاعاتی (Informational search)
- جستجوی نقطه پرش (Jump Point Search)
- *A برنامهریزی طول عمر (*Lifelong Planning A)
- *A ساده شده حافظه محدود (*Simplified Memory bounded A)
- تتا* (*Theta)
- *A هر زمان (*Anytime A)
- *A پویای هر زمان (*Anytime Dynamic A)
- *A زمان محدود (*Time-Bounded A* | TBA)
کد الگوریتم *A در ++C
میتوان از هر ساختاری برای پیادهسازی open list و closed list استفاده کرد؛ اما برای داشتن بهترین کارایی، از ساختار داده set در C++ STL (به صورت یک درخت سرخ-سیاه پیادهسازی شده است) و «جدول درهمسازی بولین» (Boolean Hash Table) برای یک closed list استفاده شده است.
پیادهسازی الگوریتم *A نیز مشابه با الگوریتم دیکسترا است. در صورت استفاده از هرم فیبوناچی برای پیادهسازی open list به جای هرم دودویی/درخت خودمتوازن، کارایی بهتر خواهد شد (زیرا هرم فیبوناچی زمانی از درجه O(1) برای درج کردن در open list و کاهش کلید میبرد). همچنین، برای کاهش زمان مورد نیاز برای محاسبه g، از «برنامهنویسی پویا» (Dynamic Programming) استفاده خواهد شد.
1// A C++ Program to implement A* Search Algorithm
2#include<bits/stdc++.h>
3using namespace std;
4
5#define ROW 9
6#define COL 10
7
8// Creating a shortcut for int, int pair type
9typedef pair<int, int> Pair;
10
11// Creating a shortcut for pair<int, pair<int, int>> type
12typedef pair<double, pair<int, int>> pPair;
13
14// A structure to hold the neccesary parameters
15struct cell
16{
17 // Row and Column index of its parent
18 // Note that 0 <= i <= ROW-1 & 0 <= j <= COL-1
19 int parent_i, parent_j;
20 // f = g + h
21 double f, g, h;
22};
23
24// A Utility Function to check whether given cell (row, col)
25// is a valid cell or not.
26bool isValid(int row, int col)
27{
28 // Returns true if row number and column number
29 // is in range
30 return (row >= 0) && (row < ROW) &&
31 (col >= 0) && (col < COL);
32}
33
34// A Utility Function to check whether the given cell is
35// blocked or not
36bool isUnBlocked(int grid[][COL], int row, int col)
37{
38 // Returns true if the cell is not blocked else false
39 if (grid[row][col] == 1)
40 return (true);
41 else
42 return (false);
43}
44
45// A Utility Function to check whether destination cell has
46// been reached or not
47bool isDestination(int row, int col, Pair dest)
48{
49 if (row == dest.first && col == dest.second)
50 return (true);
51 else
52 return (false);
53}
54
55// A Utility Function to calculate the 'h' heuristics.
56double calculateHValue(int row, int col, Pair dest)
57{
58 // Return using the distance formula
59 return ((double)sqrt ((row-dest.first)*(row-dest.first)
60 + (col-dest.second)*(col-dest.second)));
61}
62
63// A Utility Function to trace the path from the source
64// to destination
65void tracePath(cell cellDetails[][COL], Pair dest)
66{
67 printf ("\nThe Path is ");
68 int row = dest.first;
69 int col = dest.second;
70
71 stack<Pair> Path;
72
73 while (!(cellDetails[row][col].parent_i == row
74 && cellDetails[row][col].parent_j == col ))
75 {
76 Path.push (make_pair (row, col));
77 int temp_row = cellDetails[row][col].parent_i;
78 int temp_col = cellDetails[row][col].parent_j;
79 row = temp_row;
80 col = temp_col;
81 }
82
83 Path.push (make_pair (row, col));
84 while (!Path.empty())
85 {
86 pair<int,int> p = Path.top();
87 Path.pop();
88 printf("-> (%d,%d) ",p.first,p.second);
89 }
90
91 return;
92}
93
94// A Function to find the shortest path between
95// a given source cell to a destination cell according
96// to A* Search Algorithm
97void aStarSearch(int grid[][COL], Pair src, Pair dest)
98{
99 // If the source is out of range
100 if (isValid (src.first, src.second) == false)
101 {
102 printf ("Source is invalid\n");
103 return;
104 }
105
106 // If the destination is out of range
107 if (isValid (dest.first, dest.second) == false)
108 {
109 printf ("Destination is invalid\n");
110 return;
111 }
112
113 // Either the source or the destination is blocked
114 if (isUnBlocked(grid, src.first, src.second) == false ||
115 isUnBlocked(grid, dest.first, dest.second) == false)
116 {
117 printf ("Source or the destination is blocked\n");
118 return;
119 }
120
121 // If the destination cell is the same as source cell
122 if (isDestination(src.first, src.second, dest) == true)
123 {
124 printf ("We are already at the destination\n");
125 return;
126 }
127
128 // Create a closed list and initialise it to false which means
129 // that no cell has been included yet
130 // This closed list is implemented as a boolean 2D array
131 bool closedList[ROW][COL];
132 memset(closedList, false, sizeof (closedList));
133
134 // Declare a 2D array of structure to hold the details
135 //of that cell
136 cell cellDetails[ROW][COL];
137
138 int i, j;
139
140 for (i=0; i<ROW; i++)
141 {
142 for (j=0; j<COL; j++)
143 {
144 cellDetails[i][j].f = FLT_MAX;
145 cellDetails[i][j].g = FLT_MAX;
146 cellDetails[i][j].h = FLT_MAX;
147 cellDetails[i][j].parent_i = -1;
148 cellDetails[i][j].parent_j = -1;
149 }
150 }
151
152 // Initialising the parameters of the starting node
153 i = src.first, j = src.second;
154 cellDetails[i][j].f = 0.0;
155 cellDetails[i][j].g = 0.0;
156 cellDetails[i][j].h = 0.0;
157 cellDetails[i][j].parent_i = i;
158 cellDetails[i][j].parent_j = j;
159
160 /*
161 Create an open list having information as-
162 <f, <i, j>>
163 where f = g + h,
164 and i, j are the row and column index of that cell
165 Note that 0 <= i <= ROW-1 & 0 <= j <= COL-1
166 This open list is implenented as a set of pair of pair.*/
167 set<pPair> openList;
168
169 // Put the starting cell on the open list and set its
170 // 'f' as 0
171 openList.insert(make_pair (0.0, make_pair (i, j)));
172
173 // We set this boolean value as false as initially
174 // the destination is not reached.
175 bool foundDest = false;
176
177 while (!openList.empty())
178 {
179 pPair p = *openList.begin();
180
181 // Remove this vertex from the open list
182 openList.erase(openList.begin());
183
184 // Add this vertex to the closed list
185 i = p.second.first;
186 j = p.second.second;
187 closedList[i][j] = true;
188
189 /*
190 Generating all the 8 successor of this cell
191
192 N.W N N.E
193 \ | /
194 \ | /
195 W----Cell----E
196 / | \
197 / | \
198 S.W S S.E
199
200 Cell-->Popped Cell (i, j)
201 N --> North (i-1, j)
202 S --> South (i+1, j)
203 E --> East (i, j+1)
204 W --> West (i, j-1)
205 N.E--> North-East (i-1, j+1)
206 N.W--> North-West (i-1, j-1)
207 S.E--> South-East (i+1, j+1)
208 S.W--> South-West (i+1, j-1)*/
209
210 // To store the 'g', 'h' and 'f' of the 8 successors
211 double gNew, hNew, fNew;
212
213 //----------- 1st Successor (North) ------------
214
215 // Only process this cell if this is a valid one
216 if (isValid(i-1, j) == true)
217 {
218 // If the destination cell is the same as the
219 // current successor
220 if (isDestination(i-1, j, dest) == true)
221 {
222 // Set the Parent of the destination cell
223 cellDetails[i-1][j].parent_i = i;
224 cellDetails[i-1][j].parent_j = j;
225 printf ("The destination cell is found\n");
226 tracePath (cellDetails, dest);
227 foundDest = true;
228 return;
229 }
230 // If the successor is already on the closed
231 // list or if it is blocked, then ignore it.
232 // Else do the following
233 else if (closedList[i-1][j] == false &&
234 isUnBlocked(grid, i-1, j) == true)
235 {
236 gNew = cellDetails[i][j].g + 1.0;
237 hNew = calculateHValue (i-1, j, dest);
238 fNew = gNew + hNew;
239
240 // If it isn’t on the open list, add it to
241 // the open list. Make the current square
242 // the parent of this square. Record the
243 // f, g, and h costs of the square cell
244 // OR
245 // If it is on the open list already, check
246 // to see if this path to that square is better,
247 // using 'f' cost as the measure.
248 if (cellDetails[i-1][j].f == FLT_MAX ||
249 cellDetails[i-1][j].f > fNew)
250 {
251 openList.insert( make_pair(fNew,
252 make_pair(i-1, j)));
253
254 // Update the details of this cell
255 cellDetails[i-1][j].f = fNew;
256 cellDetails[i-1][j].g = gNew;
257 cellDetails[i-1][j].h = hNew;
258 cellDetails[i-1][j].parent_i = i;
259 cellDetails[i-1][j].parent_j = j;
260 }
261 }
262 }
263
264 //----------- 2nd Successor (South) ------------
265
266 // Only process this cell if this is a valid one
267 if (isValid(i+1, j) == true)
268 {
269 // If the destination cell is the same as the
270 // current successor
271 if (isDestination(i+1, j, dest) == true)
272 {
273 // Set the Parent of the destination cell
274 cellDetails[i+1][j].parent_i = i;
275 cellDetails[i+1][j].parent_j = j;
276 printf("The destination cell is found\n");
277 tracePath(cellDetails, dest);
278 foundDest = true;
279 return;
280 }
281 // If the successor is already on the closed
282 // list or if it is blocked, then ignore it.
283 // Else do the following
284 else if (closedList[i+1][j] == false &&
285 isUnBlocked(grid, i+1, j) == true)
286 {
287 gNew = cellDetails[i][j].g + 1.0;
288 hNew = calculateHValue(i+1, j, dest);
289 fNew = gNew + hNew;
290
291 // If it isn’t on the open list, add it to
292 // the open list. Make the current square
293 // the parent of this square. Record the
294 // f, g, and h costs of the square cell
295 // OR
296 // If it is on the open list already, check
297 // to see if this path to that square is better,
298 // using 'f' cost as the measure.
299 if (cellDetails[i+1][j].f == FLT_MAX ||
300 cellDetails[i+1][j].f > fNew)
301 {
302 openList.insert( make_pair (fNew, make_pair (i+1, j)));
303 // Update the details of this cell
304 cellDetails[i+1][j].f = fNew;
305 cellDetails[i+1][j].g = gNew;
306 cellDetails[i+1][j].h = hNew;
307 cellDetails[i+1][j].parent_i = i;
308 cellDetails[i+1][j].parent_j = j;
309 }
310 }
311 }
312
313 //----------- 3rd Successor (East) ------------
314
315 // Only process this cell if this is a valid one
316 if (isValid (i, j+1) == true)
317 {
318 // If the destination cell is the same as the
319 // current successor
320 if (isDestination(i, j+1, dest) == true)
321 {
322 // Set the Parent of the destination cell
323 cellDetails[i][j+1].parent_i = i;
324 cellDetails[i][j+1].parent_j = j;
325 printf("The destination cell is found\n");
326 tracePath(cellDetails, dest);
327 foundDest = true;
328 return;
329 }
330
331 // If the successor is already on the closed
332 // list or if it is blocked, then ignore it.
333 // Else do the following
334 else if (closedList[i][j+1] == false &&
335 isUnBlocked (grid, i, j+1) == true)
336 {
337 gNew = cellDetails[i][j].g + 1.0;
338 hNew = calculateHValue (i, j+1, dest);
339 fNew = gNew + hNew;
340
341 // If it isn’t on the open list, add it to
342 // the open list. Make the current square
343 // the parent of this square. Record the
344 // f, g, and h costs of the square cell
345 // OR
346 // If it is on the open list already, check
347 // to see if this path to that square is better,
348 // using 'f' cost as the measure.
349 if (cellDetails[i][j+1].f == FLT_MAX ||
350 cellDetails[i][j+1].f > fNew)
351 {
352 openList.insert( make_pair(fNew,
353 make_pair (i, j+1)));
354
355 // Update the details of this cell
356 cellDetails[i][j+1].f = fNew;
357 cellDetails[i][j+1].g = gNew;
358 cellDetails[i][j+1].h = hNew;
359 cellDetails[i][j+1].parent_i = i;
360 cellDetails[i][j+1].parent_j = j;
361 }
362 }
363 }
364
365 //----------- 4th Successor (West) ------------
366
367 // Only process this cell if this is a valid one
368 if (isValid(i, j-1) == true)
369 {
370 // If the destination cell is the same as the
371 // current successor
372 if (isDestination(i, j-1, dest) == true)
373 {
374 // Set the Parent of the destination cell
375 cellDetails[i][j-1].parent_i = i;
376 cellDetails[i][j-1].parent_j = j;
377 printf("The destination cell is found\n");
378 tracePath(cellDetails, dest);
379 foundDest = true;
380 return;
381 }
382
383 // If the successor is already on the closed
384 // list or if it is blocked, then ignore it.
385 // Else do the following
386 else if (closedList[i][j-1] == false &&
387 isUnBlocked(grid, i, j-1) == true)
388 {
389 gNew = cellDetails[i][j].g + 1.0;
390 hNew = calculateHValue(i, j-1, dest);
391 fNew = gNew + hNew;
392
393 // If it isn’t on the open list, add it to
394 // the open list. Make the current square
395 // the parent of this square. Record the
396 // f, g, and h costs of the square cell
397 // OR
398 // If it is on the open list already, check
399 // to see if this path to that square is better,
400 // using 'f' cost as the measure.
401 if (cellDetails[i][j-1].f == FLT_MAX ||
402 cellDetails[i][j-1].f > fNew)
403 {
404 openList.insert( make_pair (fNew,
405 make_pair (i, j-1)));
406
407 // Update the details of this cell
408 cellDetails[i][j-1].f = fNew;
409 cellDetails[i][j-1].g = gNew;
410 cellDetails[i][j-1].h = hNew;
411 cellDetails[i][j-1].parent_i = i;
412 cellDetails[i][j-1].parent_j = j;
413 }
414 }
415 }
416
417 //----------- 5th Successor (North-East) ------------
418
419 // Only process this cell if this is a valid one
420 if (isValid(i-1, j+1) == true)
421 {
422 // If the destination cell is the same as the
423 // current successor
424 if (isDestination(i-1, j+1, dest) == true)
425 {
426 // Set the Parent of the destination cell
427 cellDetails[i-1][j+1].parent_i = i;
428 cellDetails[i-1][j+1].parent_j = j;
429 printf ("The destination cell is found\n");
430 tracePath (cellDetails, dest);
431 foundDest = true;
432 return;
433 }
434
435 // If the successor is already on the closed
436 // list or if it is blocked, then ignore it.
437 // Else do the following
438 else if (closedList[i-1][j+1] == false &&
439 isUnBlocked(grid, i-1, j+1) == true)
440 {
441 gNew = cellDetails[i][j].g + 1.414;
442 hNew = calculateHValue(i-1, j+1, dest);
443 fNew = gNew + hNew;
444
445 // If it isn’t on the open list, add it to
446 // the open list. Make the current square
447 // the parent of this square. Record the
448 // f, g, and h costs of the square cell
449 // OR
450 // If it is on the open list already, check
451 // to see if this path to that square is better,
452 // using 'f' cost as the measure.
453 if (cellDetails[i-1][j+1].f == FLT_MAX ||
454 cellDetails[i-1][j+1].f > fNew)
455 {
456 openList.insert( make_pair (fNew,
457 make_pair(i-1, j+1)));
458
459 // Update the details of this cell
460 cellDetails[i-1][j+1].f = fNew;
461 cellDetails[i-1][j+1].g = gNew;
462 cellDetails[i-1][j+1].h = hNew;
463 cellDetails[i-1][j+1].parent_i = i;
464 cellDetails[i-1][j+1].parent_j = j;
465 }
466 }
467 }
468
469 //----------- 6th Successor (North-West) ------------
470
471 // Only process this cell if this is a valid one
472 if (isValid (i-1, j-1) == true)
473 {
474 // If the destination cell is the same as the
475 // current successor
476 if (isDestination (i-1, j-1, dest) == true)
477 {
478 // Set the Parent of the destination cell
479 cellDetails[i-1][j-1].parent_i = i;
480 cellDetails[i-1][j-1].parent_j = j;
481 printf ("The destination cell is found\n");
482 tracePath (cellDetails, dest);
483 foundDest = true;
484 return;
485 }
486
487 // If the successor is already on the closed
488 // list or if it is blocked, then ignore it.
489 // Else do the following
490 else if (closedList[i-1][j-1] == false &&
491 isUnBlocked(grid, i-1, j-1) == true)
492 {
493 gNew = cellDetails[i][j].g + 1.414;
494 hNew = calculateHValue(i-1, j-1, dest);
495 fNew = gNew + hNew;
496
497 // If it isn’t on the open list, add it to
498 // the open list. Make the current square
499 // the parent of this square. Record the
500 // f, g, and h costs of the square cell
501 // OR
502 // If it is on the open list already, check
503 // to see if this path to that square is better,
504 // using 'f' cost as the measure.
505 if (cellDetails[i-1][j-1].f == FLT_MAX ||
506 cellDetails[i-1][j-1].f > fNew)
507 {
508 openList.insert( make_pair (fNew, make_pair (i-1, j-1)));
509 // Update the details of this cell
510 cellDetails[i-1][j-1].f = fNew;
511 cellDetails[i-1][j-1].g = gNew;
512 cellDetails[i-1][j-1].h = hNew;
513 cellDetails[i-1][j-1].parent_i = i;
514 cellDetails[i-1][j-1].parent_j = j;
515 }
516 }
517 }
518
519 //----------- 7th Successor (South-East) ------------
520
521 // Only process this cell if this is a valid one
522 if (isValid(i+1, j+1) == true)
523 {
524 // If the destination cell is the same as the
525 // current successor
526 if (isDestination(i+1, j+1, dest) == true)
527 {
528 // Set the Parent of the destination cell
529 cellDetails[i+1][j+1].parent_i = i;
530 cellDetails[i+1][j+1].parent_j = j;
531 printf ("The destination cell is found\n");
532 tracePath (cellDetails, dest);
533 foundDest = true;
534 return;
535 }
536
537 // If the successor is already on the closed
538 // list or if it is blocked, then ignore it.
539 // Else do the following
540 else if (closedList[i+1][j+1] == false &&
541 isUnBlocked(grid, i+1, j+1) == true)
542 {
543 gNew = cellDetails[i][j].g + 1.414;
544 hNew = calculateHValue(i+1, j+1, dest);
545 fNew = gNew + hNew;
546
547 // If it isn’t on the open list, add it to
548 // the open list. Make the current square
549 // the parent of this square. Record the
550 // f, g, and h costs of the square cell
551 // OR
552 // If it is on the open list already, check
553 // to see if this path to that square is better,
554 // using 'f' cost as the measure.
555 if (cellDetails[i+1][j+1].f == FLT_MAX ||
556 cellDetails[i+1][j+1].f > fNew)
557 {
558 openList.insert(make_pair(fNew,
559 make_pair (i+1, j+1)));
560
561 // Update the details of this cell
562 cellDetails[i+1][j+1].f = fNew;
563 cellDetails[i+1][j+1].g = gNew;
564 cellDetails[i+1][j+1].h = hNew;
565 cellDetails[i+1][j+1].parent_i = i;
566 cellDetails[i+1][j+1].parent_j = j;
567 }
568 }
569 }
570
571 //----------- 8th Successor (South-West) ------------
572
573 // Only process this cell if this is a valid one
574 if (isValid (i+1, j-1) == true)
575 {
576 // If the destination cell is the same as the
577 // current successor
578 if (isDestination(i+1, j-1, dest) == true)
579 {
580 // Set the Parent of the destination cell
581 cellDetails[i+1][j-1].parent_i = i;
582 cellDetails[i+1][j-1].parent_j = j;
583 printf("The destination cell is found\n");
584 tracePath(cellDetails, dest);
585 foundDest = true;
586 return;
587 }
588
589 // If the successor is already on the closed
590 // list or if it is blocked, then ignore it.
591 // Else do the following
592 else if (closedList[i+1][j-1] == false &&
593 isUnBlocked(grid, i+1, j-1) == true)
594 {
595 gNew = cellDetails[i][j].g + 1.414;
596 hNew = calculateHValue(i+1, j-1, dest);
597 fNew = gNew + hNew;
598
599 // If it isn’t on the open list, add it to
600 // the open list. Make the current square
601 // the parent of this square. Record the
602 // f, g, and h costs of the square cell
603 // OR
604 // If it is on the open list already, check
605 // to see if this path to that square is better,
606 // using 'f' cost as the measure.
607 if (cellDetails[i+1][j-1].f == FLT_MAX ||
608 cellDetails[i+1][j-1].f > fNew)
609 {
610 openList.insert(make_pair(fNew,
611 make_pair(i+1, j-1)));
612
613 // Update the details of this cell
614 cellDetails[i+1][j-1].f = fNew;
615 cellDetails[i+1][j-1].g = gNew;
616 cellDetails[i+1][j-1].h = hNew;
617 cellDetails[i+1][j-1].parent_i = i;
618 cellDetails[i+1][j-1].parent_j = j;
619 }
620 }
621 }
622 }
623
624 // When the destination cell is not found and the open
625 // list is empty, then we conclude that we failed to
626 // reach the destiantion cell. This may happen when the
627 // there is no way to destination cell (due to blockages)
628 if (foundDest == false)
629 printf("Failed to find the Destination Cell\n");
630
631 return;
632}
633
634
635// Driver program to test above function
636int main()
637{
638 /* Description of the Grid-
639 1--> The cell is not blocked
640 0--> The cell is blocked */
641 int grid[ROW][COL] =
642 {
643 { 1, 0, 1, 1, 1, 1, 0, 1, 1, 1 },
644 { 1, 1, 1, 0, 1, 1, 1, 0, 1, 1 },
645 { 1, 1, 1, 0, 1, 1, 0, 1, 0, 1 },
646 { 0, 0, 1, 0, 1, 0, 0, 0, 0, 1 },
647 { 1, 1, 1, 0, 1, 1, 1, 0, 1, 0 },
648 { 1, 0, 1, 1, 1, 1, 0, 1, 0, 0 },
649 { 1, 0, 0, 0, 0, 1, 0, 0, 0, 1 },
650 { 1, 0, 1, 1, 1, 1, 0, 1, 1, 1 },
651 { 1, 1, 1, 0, 0, 0, 1, 0, 0, 1 }
652 };
653
654 // Source is the left-most bottom-most corner
655 Pair src = make_pair(8, 0);
656
657 // Destination is the left-most top-most corner
658 Pair dest = make_pair(0, 0);
659
660 aStarSearch(grid, src, dest);
661
662 return(0);
663}کد الگوریتم *A در پایتون
1from queue import PriorityQueue
2
3#Creating Base Class
4class State(object):
5 def __init__(self, value, parent, start = 0, goal = 0):
6 self.children = []
7 self.parent = parent
8 self.value = value
9 self.dist = 0
10 if parent:
11 self.start = parent.start
12 self.goal = parent.goal
13 self.path = parent.path[:]
14 self.path.append(value)
15
16 else:
17 self.path = [value]
18 self.start = start
19 self.goal = goal
20
21 def GetDistance(self):
22 pass
23 def CreateChildren(self):
24 pass
25
26
27# Creating subclass
28class State_String(State):
29 def __init__(self, value, parent, start = 0, goal = 0 ):
30 super(State_String, self).__init__(value, parent, start, goal)
31 self.dist = self.GetDistance()
32
33 def GetDistance(self):
34 if self.value == self.goal:
35 return 0
36 dist = 0
37 for i in range(len(self.goal)):
38 letter = self.goal[i]
39 dist += abs(i - self.value.index(letter))
40 return dist
41
42 def CreateChildren(self):
43 if not self.children:
44 for i in range(len(self.goal)-1):
45 val = self.value
46 val = val[:i] + val[i+1] + val[i] + val[i+2:]
47 child = State_String(val, self)
48 self.children.append(child)
49
50# Creating a class that hold the final magic
51class A_Star_Solver:
52 def __init__(self, start, goal):
53 self.path = []
54 self.vistedQueue =[]
55 self.priorityQueue = PriorityQueue()
56 self.start = start
57 self.goal = goal
58
59 def Solve(self):
60 startState = State_String(self.start,0,self.start,self.goal)
61
62 count = 0
63 self.priorityQueue.put((0,count, startState))
64 while(not self.path and self.priorityQueue.qsize()):
65 closesetChild = self.priorityQueue.get()[2]
66 closesetChild.CreateChildren()
67 self.vistedQueue.append(closesetChild.value)
68 for child in closesetChild.children:
69 if child.value not in self.vistedQueue:
70 count += 1
71 if not child.dist:
72 self.path = child.path
73 break
74 self.priorityQueue.put((child.dist,count,child))
75 if not self.path:
76 print("Goal Of is not possible !" + self.goal )
77 return self.path
78
79# Calling all the existing stuffs
80if __name__ == "__main__":
81 start1 = "hema"
82 goal1 = "mahe"
83 print("Starting....")
84 a = A_Star_Solver(start1,goal1)
85 a.Solve()
86 for i in range(len(a.path)):
87 print("{0}){1}".format(i,a.path[i]))کد الگوریتم *A در جاوا
1/** Find the path from start to goal using A-Star search
2 *
3 * @param start The starting location
4 * @param goal The goal location
5 * @return The list of intersections that form the shortest path from
6 * start to goal (including both start and goal).
7 */
8 public List<GeographicPoint> aStarSearch(GeographicPoint start,
9 GeographicPoint goal)
10 {
11
12 MapNode startNode = pointNodeMap.get(start);
13 MapNode endNode = pointNodeMap.get(goal);
14
15 // setup for A*
16 HashMap<MapNode,MapNode> parentMap = new HashMap<MapNode,MapNode>();
17 HashSet<MapNode> visited = new HashSet<MapNode>();
18 Map<MapNode, Double> distances = initializeAllToInfinity();
19
20 Queue<MapNode> priorityQueue = initQueue();
21
22 // enque StartNode, with distance 0
23 startNode.setDistanceToStart(new Double(0));
24 distances.put(startNode, new Double(0));
25 priorityQueue.add(startNode);
26 MapNode current = null;
27
28 while (!priorityQueue.isEmpty()) {
29 current = priorityQueue.remove();
30
31 if (!visited.contains(current) ){
32 visited.add(current);
33 // if last element in PQ reached
34 if (current.equals(endNode)) return reconstructPath(parentMap, startNode, endNode, 0);
35
36 Set<MapNode> neighbors = getNeighbors(current);
37 for (MapNode neighbor : neighbors) {
38 if (!visited.contains(neighbor) ){
39
40 // calculate predicted distance to the end node
41 double predictedDistance = neighbor.getLocation().distance(endNode.getLocation());
42
43 // 1. calculate distance to neighbor. 2. calculate dist from start node
44 double neighborDistance = current.calculateDistance(neighbor);
45 double totalDistance = current.getDistanceToStart() + neighborDistance + predictedDistance;
46
47 // check if distance smaller
48 if(totalDistance < distances.get(neighbor) ){
49 // update n's distance
50 distances.put(neighbor, totalDistance);
51 // used for PriorityQueue
52 neighbor.setDistanceToStart(totalDistance);
53 neighbor.setPredictedDistance(predictedDistance);
54 // set parent
55 parentMap.put(neighbor, current);
56 // enqueue
57 priorityQueue.add(neighbor);
58 }
59 }
60 }
61 }
62 }
63 return null;
64 }اگر مطلب بالا برای شما مفید بوده، آموزشهای زیر نیز به شما پیشنهاد میشود:
- مجموعه آموزشهای هوش مصنوعی
- آموزش هوش مصنوعی – تکمیلی
- مجموعه آموزشهای الگوریتمهای بهینهسازی هوشمند
- شبیه سازی تبرید (Simulated Annealing) — به زبان ساده
- جست و جوی هیوریستیک (Heuristic Search) در پایتون — راهنمای کاربردی
- الگوریتم دایجسترا (Dijkstra) — از صفر تا صد
^^













توضیخات بسیار عالی و کامل بود
ممنون
خیلی عالی بود
ممنون از توضیحات جامع و کاملتون