مرتب سازی حبابی و پیاده سازی آن — از صفر تا صد

«مرتب‌سازی حبابی» (Bubble Sort)، یکی از انواع الگوریتم‌های مرتب‌سازی محسوب می‌شود. این الگوریتم مرتب‌سازی از جمله الگوریتم‌های مبتنی بر مقایسه است که در آن، جفت عنصرهای هم‌جوار با یکدیگر مقایسه شده و در صورتی که دارای ترتیب صحیحی نباشند، با یکدیگر جا به جا می‌شوند. الگوریتم مرتب سازی حبابی برای مجموعه داده‌های بزرگ مناسب نیست، زیرا پیچیدگی زمانی آن در حالت میانگین و بدترین حالت برابر با (Ο(n² است، که در آن n تعداد کل عناصر مجموعه داده محسوب می‌شود. در این مطلب، ابتدا یک مثال از الگوریتم مرتب‌سازی حبابی ارائه و سپس، «روندنما» (Flow Chart)، شبه کد و پیاده‌سازی آن در زبان‌های «پایتون» (Python)، «جاوا» (Java)، «سی» (C) و «سی‌پلاس‌پلاس» (++C)، «پی‌اچ‌پی» (PHP) و «سی‌شارپ» (#C) ارائه شده است. شایان توجه است که الگوریتم‌های مرتب‌سازی از جمله مباحث بسیار مهم در «ساختمان داده» (Data Structure) هستند.

الگوریتم مرتب سازی حبابی چطور کار می‌کند؟

برای تشریح چگونگی عملکرد الگوریتم مرتب سازی حبابی، از یک مثال استفاده شده است. در این مثال، یک آرایه غیر مرتب در نظر گرفته شده است. با توجه به اینکه الگوریتم مرتب سازی حبابی از مرتبه (Ο(n² است، آرایه انتخاب شده کوچک در نظر گرفته می‌شود. آرایه در نظر گرفته شده: ( ۴ ۲ ۸ ۱ ۵ ) است. مرتب‌سازی حبابی برای این آرایه، به صورت زیر انجام می‌شود.

۱. ابتدا، دو عنصر اول آرایه با یکدیگر مقایسه می‌شوند و با توجه به آنکه ۵ از ۱ بزرگتر است (۱<۵)، این دو عنصر با یکدیگر جا به جا می‌شوند.

( 5 1 4 2 8 ) –> ( 1 5 4 2 8 )

۲. در اینجا، عناصر دوم و سوم آرایه مقایسه می‌شوند و با توجه به اینکه ۵ از ۴ بزرگ‌تر است (۴<۵)، این دو عنصر با یکدیگر جا به جا می‌شوند.

( 1 5 4 2 8 ) –> ( 1 4 5 2 8 )

۳. اکنون، عنصر سوم و چهارم آرایه مقایسه می‌شوند و با توجه به اینکه ۲ از ۵ کوچک‌تر است (۲<۵)، این دو عنصر با یکدیگر جا به جا می‌شوند.

( 1 4 5 2 8 ) –>  ( 1 4 2 5 8 )

۴. در اینجا، عنصر چهارم و پنجم آرایه مقایسه می‌شود و چون ۵ از ۸ کوچک‌تر است (۵<۸) دو عنصر در جای خود بدون هر گونه جا به جایی باقی می‌مانند؛ چون در واقع، ترتیب (صعودی) در آن‌ها رعایت شده است.

( 1 4 2 5 8 ) –> ( 1 4 2 5 8 )

اکنون یک دور کامل در آرایه زده شد. دومین دور نیز به شیوه بیان شده در بالا انجام می‌شود.

۱. جا به جایی اتفاق نمی‌افتد.

( 1 4 2 5 8 ) –> ( 1 4 2 5 8 )

۲. با توجه به بزرگ‌تر بودن ۴ از ۲ (۲<۴)، این دو عنصر با یکدیگر جا به جا می‌شوند.

( 1 4 2 5 8 ) –> ( 1 2 4 5 8 )

۳. جا به جایی اتفاق نمی‌افتد.

( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )

۴. جا به جایی اتفاق نمی‌افتد.

( 1 2 4 5 8 ) –>  ( 1 2 4 5 8 )

در حال حاضر، آرایه مرتب شده است، اما الگوریتم نمی‌داند که آیا کار به پایان رسیده یا خیر؛ بنابراین، به یک دور کامل دیگر بدون انجام هرگونه جا به جایی نیاز دارد تا بفهمد که مرتب‌سازی با موفقیت به پایان رسیده است.

( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )

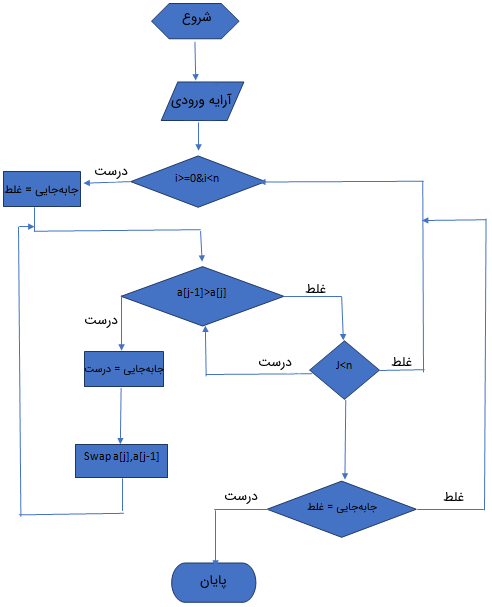
شبه کد الگوریتم مرتب سازی حبابی

Bubble Sort(a[],n)
	For i=0 to n-1
	Swap=false
	For j=i+1 to n
		if a[j-1] >a[j]
			Swap(a[j-1],a[j])
			Swap=true
		Break if not swapped

در ادامه، پیاده‌سازی الگوریتم مرتب سازی حبابی در زبان‌های برنامه‌نویسی گوناگون انجام شده و آرایه {۹۰ ,۱۱ ,۲۲ ,12 ,۲۵ ,۳۴ ,۶۴} به عنوان ورودی به قطعه کدها داده شده است. بنابراین، خروجی نهایی همه قطعه کدها، به صورت زیر خواهد بود.

11 12 22 25 34 64 90

پیاده‌سازی الگوریتم مرتب سازی حبابی در پایتون

# Python program for implementation of Bubble Sort 
  
def bubbleSort(arr): 
    n = len(arr) 
  
    # Traverse through all array elements 
    for i in range(n): 
  
        # Last i elements are already in place 
        for j in range(0, n-i-1): 
  
            # traverse the array from 0 to n-i-1 
            # Swap if the element found is greater 
            # than the next element 
            if arr[j] > arr[j+1] : 
                arr[j], arr[j+1] = arr[j+1], arr[j] 
  
# Driver code to test above 
arr = [64, 34, 25, 12, 22, 11, 90] 
  
bubbleSort(arr) 
  
print ("Sorted array is:") 
for i in range(len(arr)): 
    print ("%d" %arr[i]),

پیاده‌سازی الگوریتم مرتب سازی حبابی در جاوا

// Java program for implementation of Bubble Sort 
class BubbleSort 
{ 
    void bubbleSort(int arr[]) 
    { 
        int n = arr.length; 
        for (int i = 0; i < n-1; i++) 
            for (int j = 0; j < n-i-1; j++) 
                if (arr[j] > arr[j+1]) 
                { 
                    // swap arr[j+1] and arr[i] 
                    int temp = arr[j]; 
                    arr[j] = arr[j+1]; 
                    arr[j+1] = temp; 
                } 
    } 
  
    /* Prints the array */
    void printArray(int arr[]) 
    { 
        int n = arr.length; 
        for (int i=0; i<n; ++i) 
            System.out.print(arr[i] + " "); 
        System.out.println(); 
    } 
  
    // Driver method to test above 
    public static void main(String args[]) 
    { 
        BubbleSort ob = new BubbleSort(); 
        int arr[] = {64, 34, 25, 12, 22, 11, 90}; 
        ob.bubbleSort(arr); 
        System.out.println("Sorted array"); 
        ob.printArray(arr); 
    } 
} 
/* This code is contributed by Rajat Mishra */

پیاده‌سازی الگوریتم مرتب سازی حبابی در C و ++C

// C program for implementation of Bubble sort 
#include <stdio.h> 
  
void swap(int *xp, int *yp) 
{ 
    int temp = *xp; 
    *xp = *yp; 
    *yp = temp; 
} 
  
// A function to implement bubble sort 
void bubbleSort(int arr[], int n) 
{ 
   int i, j; 
   for (i = 0; i < n-1; i++)       
  
       // Last i elements are already in place    
       for (j = 0; j < n-i-1; j++)  
           if (arr[j] > arr[j+1]) 
              swap(&arr[j], &arr[j+1]); 
} 
  
/* Function to print an array */
void printArray(int arr[], int size) 
{ 
    int i; 
    for (i=0; i < size; i++) 
        printf("%d ", arr[i]); 
    printf("n"); 
} 
  
// Driver program to test above functions 
int main() 
{ 
    int arr[] = {64, 34, 25, 12, 22, 11, 90}; 
    int n = sizeof(arr)/sizeof(arr[0]); 
    bubbleSort(arr, n); 
    printf("Sorted array: \n"); 
    printArray(arr, n); 
    return 0; 
}

پیاده‌سازی الگوریتم مرتب سازی حبابی در PHP

<?php  
// PHP program for implementation  
// of Bubble Sort 
  
function bubbleSort(&$arr) 
{ 
    $n = sizeof($arr); 
  
    // Traverse through all array elements 
    for($i = 0; $i < $n; $i++)  
    { 
        // Last i elements are already in place 
        for ($j = 0; $j < $n - $i - 1; $j++)  
        { 
            // traverse the array from 0 to n-i-1 
            // Swap if the element found is greater 
            // than the next element 
            if ($arr[$j] > $arr[$j+1]) 
            { 
                $t = $arr[$j]; 
                $arr[$j] = $arr[$j+1]; 
                $arr[$j+1] = $t; 
            } 
        } 
    } 
} 
  
// Driver code to test above 
$arr = array(64, 34, 25, 12, 22, 11, 90); 
  
$len = sizeof($arr); 
bubbleSort($arr); 
  
echo "Sorted array : \n"; 
  
for ($i = 0; $i < $len; $i++) 
    echo $arr[$i]." ";  
  
// This code is contributed by ChitraNayal. 
?>

پیاده‌سازی الگوریتم مرتب سازی حبابی در سی شارپ

// C# program for implementation  
// of Bubble Sort 
using System; 
  
class GFG 
{  
    static void bubbleSort(int []arr) 
    { 
        int n = arr.Length; 
        for (int i = 0; i < n - 1; i++) 
            for (int j = 0; j < n - i - 1; j++) 
                if (arr[j] > arr[j + 1]) 
                { 
                    // swap temp and arr[i] 
                    int temp = arr[j]; 
                    arr[j] = arr[j + 1]; 
                    arr[j + 1] = temp; 
                } 
    } 
  
    /* Prints the array */
    static void printArray(int []arr) 
    { 
        int n = arr.Length; 
        for (int i = 0; i < n; ++i) 
            Console.Write(arr[i] + " "); 
        Console.WriteLine(); 
    } 
  
    // Driver method 
    public static void Main() 
    { 
        int []arr = {64, 34, 25, 12, 22, 11, 90}; 
        bubbleSort(arr); 
        Console.WriteLine("Sorted array"); 
        printArray(arr); 
    } 
  
} 
  
// This code is contributed by Sam007

پیاده سازی بهینه الگوریتم مرتب سازی حبابی

تابع معرفی شده در بالا در حالت متوسط و بدترین حالت، برابر با (O(n*n است. بدترین حالت تنها هنگامی به وقوع می‌پیوندد که آرایه به ترتیب معکوسی مرتب شده باشد. پیچیدگی زمانی تابع مذکور در بهترین حالت برابر با (O(n است و این حالت تنها هنگامی اتفاق می‌افتد که آرایه مرتب شده باشد. تابع بالا را می‌توان به این شکل بهینه کرد که اگر حلقه داخلی منجر به هیچ جا به جایی نشود، فرایند متوقف شود. در ادامه، نمونه کد مربوط به تابع بهینه شده، در زبان‌های برنامه‌نویسی گوناگون از جمله پایتون (نسخه ۳) ارائه شده است.

پیاده‌سازی بهینه الگوریتم مرتب سازی حبابی در پایتون

# Python3 Optimized implementation 
# of Bubble sort 
  
# An optimized version of Bubble Sort 
def bubbleSort(arr): 
    n = len(arr) 
   
    # Traverse through all array elements 
    for i in range(n): 
        swapped = False
  
        # Last i elements are already 
        #  in place 
        for j in range(0, n-i-1): 
   
            # traverse the array from 0 to 
            # n-i-1. Swap if the element  
            # found is greater than the 
            # next element 
            if arr[j] > arr[j+1] : 
                arr[j], arr[j+1] = arr[j+1], arr[j] 
                swapped = True
  
        # IF no two elements were swapped 
        # by inner loop, then break 
        if swapped == False: 
            break
           
# Driver code to test above 
arr = [64, 34, 25, 12, 22, 11, 90] 
   
bubbleSort(arr) 
   
print ("Sorted array :") 
for i in range(len(arr)): 
    print ("%d" %arr[i],end=" ") 
  
# This code is contributed by Shreyanshi Arun

پیاده‌سازی بهینه الگوریتم مرتب سازی حبابی در جاوا

// Optimized java implementation 
// of Bubble sort 
import java.io.*; 
  
class GFG  
{ 
    // An optimized version of Bubble Sort 
    static void bubbleSort(int arr[], int n) 
    { 
        int i, j, temp; 
        boolean swapped; 
        for (i = 0; i < n - 1; i++)  
        { 
            swapped = false; 
            for (j = 0; j < n - i - 1; j++)  
            { 
                if (arr[j] > arr[j + 1])  
                { 
                    // swap arr[j] and arr[j+1] 
                    temp = arr[j]; 
                    arr[j] = arr[j + 1]; 
                    arr[j + 1] = temp; 
                    swapped = true; 
                } 
            } 
  
            // IF no two elements were  
            // swapped by inner loop, then break 
            if (swapped == false) 
                break; 
        } 
    } 
  
    // Function to print an array  
    static void printArray(int arr[], int size) 
    { 
        int i; 
        for (i = 0; i < size; i++) 
            System.out.print(arr[i] + " "); 
        System.out.println(); 
    } 
  
    // Driver program 
    public static void main(String args[]) 
    { 
        int arr[] = { 64, 34, 25, 12, 22, 11, 90 }; 
        int n = arr.length; 
        bubbleSort(arr, n); 
        System.out.println("Sorted array: "); 
        printArray(arr, n); 
    } 
} 
  
  
// This code is contributed  
// by Nikita Tiwari.

پیاده‌سازی بهینه الگوریتم مرتب سازی حبابی در ++C

// Optimized implementation of Bubble sort 
#include <stdio.h> 
  
void swap(int *xp, int *yp) 
{ 
    int temp = *xp; 
    *xp = *yp; 
    *yp = temp; 
} 
  
// An optimized version of Bubble Sort 
void bubbleSort(int arr[], int n) 
{ 
   int i, j; 
   bool swapped; 
   for (i = 0; i < n-1; i++) 
   { 
     swapped = false; 
     for (j = 0; j < n-i-1; j++) 
     { 
        if (arr[j] > arr[j+1]) 
        { 
           swap(&arr[j], &arr[j+1]); 
           swapped = true; 
        } 
     } 
  
     // IF no two elements were swapped by inner loop, then break 
     if (swapped == false) 
        break; 
   } 
} 
  
/* Function to print an array */
void printArray(int arr[], int size) 
{ 
    int i; 
    for (i=0; i < size; i++) 
        printf("%d ", arr[i]); 
    printf("n"); 
} 
  
// Driver program to test above functions 
int main() 
{ 
    int arr[] = {64, 34, 25, 12, 22, 11, 90}; 
    int n = sizeof(arr)/sizeof(arr[0]); 
    bubbleSort(arr, n); 
    printf("Sorted array: \n"); 
    printArray(arr, n); 
    return 0; 
}

پیاده‌سازی بهینه الگوریتم مرتب سازی حبابی در PHP

<?php  
// PHP Optimized implementation 
// of Bubble sort 
  
// An optimized version of Bubble Sort 
function bubbleSort(&$arr) 
{ 
    $n = sizeof($arr); 
  
    // Traverse through all array elements 
    for($i = 0; $i < $n; $i++) 
    { 
        $swapped = False; 
  
        // Last i elements are already 
        // in place 
        for ($j = 0; $j < $n - $i - 1; $j++) 
        { 
              
            // traverse the array from 0 to 
            // n-i-1. Swap if the element  
            // found is greater than the 
            // next element 
            if ($arr[$j] > $arr[$j+1]) 
            { 
                $t = $arr[$j]; 
                $arr[$j] = $arr[$j+1]; 
                $arr[$j+1] = $t; 
                $swapped = True; 
            } 
        } 
  
        // IF no two elements were swapped 
        // by inner loop, then break 
        if ($swapped == False) 
            break; 
    } 
} 
          
// Driver code to test above 
$arr = array(64, 34, 25, 12, 22, 11, 90);  
$len = sizeof($arr); 
bubbleSort($arr); 
  
echo "Sorted array : \n"; 
  
for($i = 0; $i < $len; $i++) 
    echo $arr[$i]." "; 
      
// This code is contributed by ChitraNayal. 
?>

پیاده‌سازی بهینه الگوریتم مرتب سازی حبابی در #C

// Optimized C# implementation 
// of Bubble sort 
using System; 
  
class GFG 
{  
    // An optimized version of Bubble Sort 
    static void bubbleSort(int []arr, int n) 
    { 
        int i, j, temp; 
        bool swapped; 
        for (i = 0; i < n - 1; i++)  
        { 
            swapped = false; 
            for (j = 0; j < n - i - 1; j++)  
            { 
                if (arr[j] > arr[j + 1])  
                { 
                    // swap arr[j] and arr[j+1] 
                    temp = arr[j]; 
                    arr[j] = arr[j + 1]; 
                    arr[j + 1] = temp; 
                    swapped = true; 
                } 
            } 
  
            // IF no two elements were  
            // swapped by inner loop, then break 
            if (swapped == false) 
                break; 
        } 
    } 
  
    // Function to print an array  
    static void printArray(int []arr, int size) 
    { 
        int i; 
        for (i = 0; i < size; i++) 
            Console.Write(arr[i] + " "); 
        Console.WriteLine(); 
    } 
  
    // Driver method  
    public static void Main() 
    { 
        int []arr = {64, 34, 25, 12, 22, 11, 90}; 
        int n = arr.Length; 
        bubbleSort(arr,n); 
        Console.WriteLine("Sorted array"); 
        printArray(arr,n); 
    } 
  
} 
// This code is contributed by Sam007

جمع‌بندی

الگوریتم مرتب‌سازی حبابی با توجه به سادگی که دارد، معمولا برای معرفی مفهوم مرتب‌سازی مورد استفاده قرار می‌گیرد. در گرافیک کامپیوتری، این الگوریتم مرتب‌سازی با توجه به توانایی که برای تشخیص خطاهای خیلی کوچک (مانند جا به جایی تنها دو عنصر) در آرایه‌های تقریبا مرتب شده و رفع آن با پیچیدگی خطی (2n) دارد، از محبوبیت زیادی برخوردار است. برای مثال، در الگوریتم «پر کردن چند ضلعی» (Polygon Filling Algorithm) که خط‌های محدود کننده به وسیله مختصات x در یک خط اسکن مشخص مرتب‌سازی شده‌اند (خطی موازی محور x) و با افزایش y ترتیب آن‌ها در تقاطع دو خط تغییر می‌کند (دو عنصر جا به جا می‌شوند)، مورد استفاده قرار می‌گیرد.

• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• آموزش ساختمان داده‌ها با C و ++C (همراه با حل نمونه سوالات کنکور ارشد)
• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• ساختمان داده (Data Structure) — راهنمای جامع و کاربردی
• آموزش ساختمان داده — مجموعه مقالات جامع وبلاگ فرادرس

^^