دنباله فیبوناچی چیست؟ — اعداد فیبوناچی، الگوی فیبوناچی

در ریاضیات، دنبالهها و رفتار آنها بسیار مورد توجه قرار گرفته است. بخصوص دنبالهها و سریهایی که در طبیعت نیز به وضوح دیده میشوند. یکی از این سریها، دنباله فیبوناچی است که در بسیاری از تناسبها (مثل اعداد طلایی) دیده میشود. در این متن از سری مطالب ریاضی مجله فرادرس میخواهیم بدانیم که دنباله فیبوناچی چیست ؟ اعداد فیبوناچی، الگوی فیبوناچی هر یک به چه معنی است و به چه کار میآیند.
برای آشنایی بیشتر با مباحث به کار رفته در این متن بهتر است مطالب دیگری از مجله فرادرس با عنوان الگوها و دنباله های متداول عددی — به زبان ساده را مطالعه کنید. همچنین خواندن سری همگرا و واگرا — از صفر تا صد و آموزش فیبوناچی در تحلیل تکنیکال بورس | به زبان ساده نیز خالی از لطف نیست.
دنباله فیبوناچی چیست ؟
اعداد فیبوناچی برای ایجاد شاخصهای فنی با استفاده از توالی ریاضی ساخته و توسط ریاضیدان ایتالیایی، «لئونارد پیزانو بوگولو» (Leonardo Pisano Bogollo) در ابتدای قرن سیزدهم معرفی شد. البته نام خانوادگی او در سالهای بعد به «فیبوناچی» (Fibonacci) تغییر یافت. در واقع فیبوناچی لقب وی به معنی «پسر بوناچی» بوده است. فیبوناچی علاوه بر شهرتی که به خاطر دنباله فیبوناچی دارد، به علت گسترش اعداد هندی – عربی (همان اعداد معمول در ریاضی امروزی 9 ,8 ,7 ,6 ,5 ,4 ,3 ,2 ,1 ) در اروپا به جای اعداد رومی ( … I, II, III, IV, V) نیز مشهور شده است.
روز 23 نوامبر (2 آذر) به نام روز فیبوناچی نامگذاری شده است. چرا که این روز در تقویم میلادی به صورت 11/23 نشان داده میشود که ابتدای دنباله فیبوناچی است.

نکته: باید اشاره کنیم که فیبوناچی اولین شخصی نبود که این دنباله را کشف کرده است و این دنباله صدها سال پیش از وی در هند شناخته شده و به کار میرفت.
توالی اعداد در سری یا دنباله فیبوناچی، با صفر و یک شروع میشود، با جمع کردن دو عدد قبلی در هر گام، یک عدد دیگر از این دنباله ایجاد خواهد شد. به عنوان مثال، قسمت اولیه دنباله 0، 1، 1، 2، 3، 5، 8، 13، 21، 34، 55، 89، 144، 233، 377 و غیره است. همانطور که میبینید از سمت راست به چپ، جمع هر دو عدد متوالی، عدد بعدی را ساخته است. این توالی را میتوان به نسبتهایی تقسیم کرد که برخی معتقدند سرنخی را درباره مکان حرکت یک بازار مالی مشخص ارائه میدهد. در مورد این موضوع در ادامه متن صحبت خواهیم کرد.
نکته: جالب است که بدانید، دنباله فیبوناچی ابتدا برای مشخص کردن جمعیت خرگوشها به کار رفت. لئونارد پیزانو، قصد داشت بداند در پایان یک سال با داشتن یک زوج خرگوش، چند خرگوش زاد و ولد کرده و تعدادشان به چه عددی میرسد.
اعداد فیبوناچی
اگر بخواهیم این دنباله را به بیان ریاضی نمایش دهیم، از رابطههای زیر کمک خواهیم گرفت. در اینجا $$F_i$$ عدد فیبوناچی در گام یا مرحله $$i$$ام است.
$$ \large F_0 = 0 $$
$$ \large F_1 = 1 $$
$$ \large F_i = F_{i-1} + F_{i-2} $$
به این ترتیب اگر مقدار $$i$$ را از صفر آغاز کنیم، دنباله یا سری فیبوناچی تولید خواهد شد.
نکته: در دنبالهای که شخص فیبوناچی ابداع کرد، $$i$$ از مقدار ۱ آغاز میشود و داریم $$F_1 = F_2 = 1 $$.
براساس رابطههای گفته شده میتوانیم ۲۱ عدد ابتدایی دنباله فیبوناچی را به صورت زیر در نظر بگیریم.
| F0 | 0 | F11 | 89 |
| F1 | 1 | F12 | 144 |
| F2 | 1 | F13 | 233 |
| F3 | 2 | F14 | 377 |
| F4 | 3 | F15 | 610 |
| F5 | 5 | F16 | 987 |
| F6 | 8 | F17 | 1597 |
| F7 | 13 | F18 | 2584 |
| F8 | 21 | F19 | 4181 |
| F9 | 34 | F20 | 6765 |
| F10 | 55 |
در تصویر زیر نمایش میزان رشد اعداد فیبوناچی را مشاهده میکنید. این نمودار را به سادگی در اکسل میتوانید ترسیم کنید.
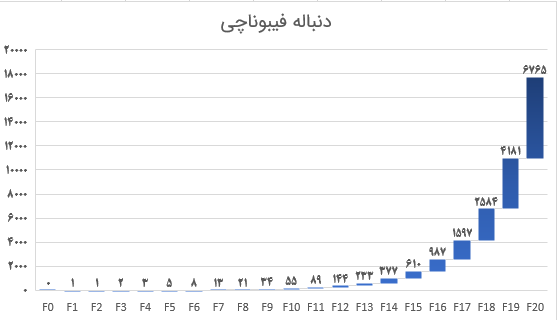
همین دنباله را میتوان برای اعداد منفی نیز ساخت. در این صورت رابطه بین مقادیر این دنباله به صورت زیر خواهد بود.
$$ \large {\displaystyle F_{-i} = (-1)^{i+1} F_{i}} $$
به این ترتیب دنبالهای به شکل زیر خواهیم داشت.
| F−8 | −21 | F0 | 0 |
| F−7 | 13 | F1 | 1 |
| F−6 | −8 | F2 | 1 |
| F−5 | 5 | F3 | 2 |
| F−4 | −3 | F4 | 3 |
| F−3 | 2 | F5 | 5 |
| F−2 | −1 | F6 | 8 |
| F−1 | 1 | F7 | 13 |
| — | — | F8 | 21 |
این بار نمودار مربوط به این دادهها را ترسیم کرده و با شکل قبلی مقایسه میکنیم.
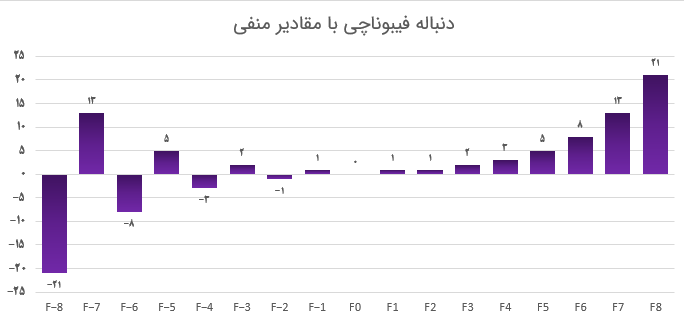
به خوبی تناوب یا تغییر مقادیر مثبت به منفی در مجموعه مقادیر منفی دنباله فیبوناچی دیده میشود. ولی برای اعداد مثبت در دنباله فیبوناچی، تناوب وجود ندارد.
به این ترتیب مشخص شد که اعداد فیبوناچی چیست و الگوی فیبوناچی به چه شکلی است. در ادامه در مورد نسبت طلایی حاصل از همگرایی نسبت اعداد فیبوناچی صحبت خواهیم کرد و در انتها نیز یکی از کاربردهای این نسبت طلایی و اعداد الگوی فیبوناچی را در بازارهای مالی و بخصوص بورس مورد بررسی قرار میدهیم.
نسبت طلایی و الگوی فیبوناچی
دنباله فیبوناچی به دلیل آن که یک نسبت خاص بین اعداد متوالی آن وجود دارد، اهمیت زیادی پیدا کرده است. این نسبت که به نام نسبت اعداد طلایی نیز شناخته میشود برابر است با 1٫618. واضح است که این نسبت از تقسیم عدد بزرگتر بر عدد کوچکتر در دنباله فیبوناچی بدست میآید.
برای مثال دو عدد متوالی (به جز صفر) را در نظر بگیرید. در اینجا ۵ و ۸ را مثال میزنیم. نسبت یا تقسیم ۸ بر ۵ برابر است با تقریبا ۱٫۶۱۸ با سه رقم اعشار. البته این عدد یک عدد گویا نیست و باید آن را از جمله مقادیر گنگ یا اصم در نظر گرفت. نکته جالب این است که این عدد اصم یا نسبت طلایی، براساس اعداد صحیح یا طبیعی ساخته شده است. به نتیجه تقسیم و بدست آمدن اعداد طلایی بعدی در ادامه توجه کنید.
$$ \large \dfrac{3}{2} \approx 1.500 $$
$$ \large \dfrac{5}{3} \approx 1.667 $$
$$ \large \dfrac{8}{5} \approx 1.6 $$
$$ \large \dfrac{13}{8} \approx 1.625 $$
$$ \large \dfrac{21}{13} \approx 1.615 $$
$$ \large \dfrac{34}{21} \approx 1.619 $$
$$ \large \dfrac{55}{34} \approx 1.618 $$
$$ \large \dfrac{89}{55} \approx 1.618 $$
$$ \large \dfrac{144}{89} \approx 1.618 $$
$$ \large \dfrac{233}{144} \approx 1.618 $$
$$ \large \dfrac{377}{233} \approx 1.618 $$
همانطور که دیده میشود، هر چه اعداد فیبوناچی بزرگتر شوند، این نسبت به ۱٫۶۱۸ نزدیکتر خواهد شد. این امر نشان میدهد که اگر نسبت طلایی را با $$\varphi$$ نشان دهیم، حد نسبت دو عدد متوالی از دنباله فیبوناچی به نسبت طلایی میل خواهد کرد. این موضوع را به صورت رابطه حدی زیر نشان میدهیم.
$$ \large {\displaystyle \lim_{i \to \infty }{\dfrac {F_{i +1}}{F_{i}}} =\varphi } $$
فرض کنید مقدار $$\varphi$$ را به صورت زیر در نظر گرفتهایم.
$$ \large {\displaystyle \varphi = {\dfrac { 1+ {\sqrt {5}} }{2}} \approx 1.61803\,39887 \ldots } $$
نکته: مقدار $$\varphi$$ را همان نسبت طلایی گویند.
به این ترتیب دنباله یا سری فیبوناچی را میتوان به شکلی نوشت که با $$\varphi$$ در رابطه باشد.
$$ \large {\displaystyle F_{i}= {\dfrac {\varphi ^{i}- \psi ^{i}}{ \varphi -\psi }} ={\dfrac { \varphi ^{i}- \psi ^{i} }{ \sqrt {5} }},} $$
که در آن $$\psi$$ با $$\varphi$$ در رابطه زیر صدق میکنند.
$$ \large {\displaystyle \psi ={\dfrac {1- {\sqrt {5}}}{2}} =1 -\varphi = -{1 \over \varphi } \approx -0.61803 \,39887 \ldots } $$
البته اگر نسبت را عکس کنیم، مقدار حاصل برابر با ۰٫۱۸۸ است. به این معنی که اگر عدد کوچکتر را به عدد بزرگتر در دنباله فیبوناچی تقسیم کنیم، دنباله حاصل از تقسیم به ۰٫۱۸۸، همگرا خواهد بود.
از آنجایی که $$\psi = - \varphi^{-1} $$ رابطه اخیر برای دنباله فیبوناچی را به صورت زیر خواهیم نوشت.
$$ \large {\displaystyle F_{n} ={ \dfrac {\varphi ^{n} -( -\varphi )^{- n}}{\sqrt {5}}} ={\dfrac {\varphi ^{n} -(-\varphi )^{-n}}{ 2\varphi -1} }} $$
نکته: توجه داشته باشید که رابطه بین $$\varphi$$ و $$\psi$$ نشانگر آن است که آنها ریشههای معادلات درجه ۲ زیر هستند. واضح است که با فاکتورگیری $$X^{n-2}$$ در معادله دوم، میتوان آن را به یک معادله درجه ۲ تبدیل کرد. البته انجام این محاسبه از حوصله این متن خارج است. بهتر است به مباحث دیگر مجله فرادرس که در رابطه با حل معادله مرتبط است، مراجعه کنید.
$$ \large {\displaystyle x^{2} = x+1 \quad , \quad x^{n} = x^{n-1} + x^{n -2}} $$
پس میتوان بین مقادیر نسبتهای فیبوناچی ($$\varphi$$) نیز یک رابطه بازگشتی (Recursion) مانند دنباله فیبوناچی نوشت.
$$ \large {\displaystyle \varphi ^{n} =\varphi ^{n- 1}+ \varphi ^{n-2}}$$
و به همین ترتیب برای $$\psi$$ نیز به رابطه زیر خواهیم رسد.
$$ \large {\displaystyle \psi ^{n} = \psi ^{n -1}+ \psi ^{n -2}}$$
در یکی از آموزشهای فرادرس که در رابطه با بورس و اوراق بهادار است، به موضوع پیشبینی بازار به کمک دنباله فیبونانچی اشاره شده است. بهتر است این فیلم آموزشی را مشاهده کنید. لینک دسترسی به این آموزش در ادامه دیده میشود.
نسبت طلایی از نظر ماهیت در همه جا موجود است و همه چیز را توصیف میکند، از تعداد رگهای برگ گرفته تا تشدید مغناطیسی چرخش در بلورهای کبالت نیوبات. همه به شکلی به اعداد فیبوناچی و همچنین نسبت طلایی مرتبط هستند. در تصویر زیر یک نمونه از نمایش نسبت طلایی در بین مربعهایی دیده میشود که قطر آنها به صورت یک منحنی به هم متصل شده است. توجه داشته باشید که طول ضلع هر یک از این مربعها، یکی از اعداد فیبوناچی است.
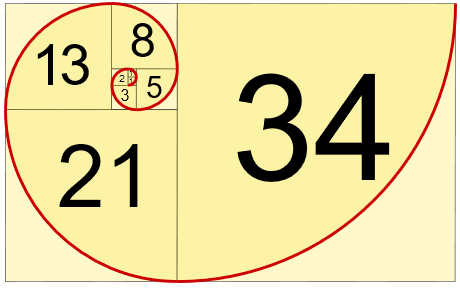
چنین مارپیچی را در طبیعت نیز میتوان یافت. برای مثال، اشکالی که در مرکز گل آفتابگردان ساخته میشود، الگوی به شکل تصویر بالا دارد.

خصوصیات جالب برای اعداد یا سری فیبوناچی
دوباره به دنباله یا سری فیبناچی نگاهی بیاندازیم.
$$ \large \{ 0 , 1 , 1 , 2, 3, 5, 8, 13, 21, 34, 55 , 89, 144, 233, 377, 610, 98, 1597, 2584, 4181, 6765, \ldots \}$$
به عنصر سوم از این دنباله نگاه کنید. مقدار آن برابر با 2 است. میتوان دید که هر عددی با فاصله ۲ از عنصر سوم این دنباله، به شکل مضرب ۲ از این عدد نوشته میشود. به بیان ریاضی خواهیم داشت.
$$ \large F_{i+3} = kF_{3} =2k $$
که در آن $$i= 3, 6 \ldots$$. به این ترتیب با تغییر مقدار $$i$$ مقدارهای بعدی به شکل زیر حاصل میشوند که همگی مضرب ۲ (یعنی مضربی از مقدار $$F_3$$) میباشند. در نتیجه مشخص است که همه آنها مقادیر زوج هستند. به این ترتیب به مجموعه زیر خواهیم رسید.
$$ \large \{ 2, 8, 34, 144, 610, \ldots \} $$
نکته: مقدار $$k$$ در رابطه بالا یک عدد طبیعی در نظر گرفته میشود. مشخص است که با اجرای عمل ضرب به شکل $$2 \times k$$، نتیجه مضربی از ۲ خواهد بود.
همین عمل را برای $$F_4=3$$ در نظر میگیریم. به نظر میرسد که هر عددی با فاصله ۴ از عنصر چهارم، مضربی از ۳ خواهد بود.
$$ \large F_{i+4} = k F_{4} =3k $$
این مجموعه نیز به شکل زیر خواهد بود.
$$ \large \{ 3, 21, 144, 987, \ldots \} $$
باز هم مضربهایی به شکل $$3k$$ برای مقادیر طبیعی از $$k$$، مقادیری هستند که همگی بر ۳ بخشپذیر بوده در نتیجه مضربهای ۳ را تشکیل میدهند.
این بار به سراغ عنصر $$F_5 = 5 $$ میریم. انتظار داریم که مقادیری با فاصله ۵ از آن، همگی مضربی از ۵ باشند. پس میتوان هر یک از آنها را به ۵ تقسیم کرد یا بیان نمود که چنین اعدادی بر ۵ بخشپذیر هستند.
$$ \large F_{i+5} = k F_{5} =5k $$
به مجموعه مقادیر زیر توجه کنید که در رابطه بالا صادق هستند. اینها همگی از مقدار ۵، ۵ شماره فاصله دارند.
$$ \large \{ 5, 55, 610, 6765, \ldots \} $$
این بار هم با توجه به مضربهایی به شکل $$5k$$ به ازاء مقادیر طبیعی $$k$$، اعداد حاصل همگی در یکان مقدار ۵ یا صفر را دارند در نتیجه بر ۵ بخشپذیر هستند.
و به این ترتیب این الگو ادامه می یابد و هر عدد فیبوناچی با i فاصله از اعداد قبلی، مضربی از $$F_i$$ است.
$$ \large F_{i+n} = k F_{n} $$
شاید محاسبه و پیدا کردن اعداد فیبوناچی ساده به نظر آید ولی همین عمل جمعکردن برای مقادیر بزرگ ممکن است با خطای محاسباتی همراه باشد. به این دلیل برای تولید اعداد فیبوناچی از رایانه و برنامههای رایانهای کمک میگیرند. به منظور دستیابی به برنامه تولید اعداد فیبوناچی میتوانید به مطلب برنامه محاسبه nامین عدد فیبوناچی — به زبان ساده مراجعه کنید. پیادهسازی اعداد فیبوناچی در این مطلب براساس زبانهای برنامهنویسی ++C، «جاوا» (Java)، «پایتون» (Python)، «سیشارپ» (#C) و «پیاچپی» (PHP) صورت گرفته است.
استفاده از اعداد فیبوناچی در بازارهای مالی
همانطور که در متن خواندید میدانید که اعداد فیبوناچی یک فرمول نیستند بلکه به عنوان یک دنباله یا توالی از اعداد محسوب میشوند. در این دنباله هر مقدار وابسته به دو مقدار قبلی خود است. اعداد و خطوط فیبوناچی در نمودارهای مربوط به بورس با نسبتهایی که در توالی یا دنباله فیبوناچی وجود دارد، ایجاد میشوند. اعداد رایج فیبوناچی در بازارهای مالی 0٫236 ، 0٫382 ، 0٫618 ، 1٫618 ، 2٫618 ، 4٫236 است. این نسبتها یا درصدها را میتوان با تقسیم اعداد خاصی در توالی یا دنباله فیبوناچی بر اعداد دیگر پیدا کرد. البته به یاد داشته باشید که اعداد 0٫5، 1٫0 و 2٫0 به طور رسمی اعداد فیبوناچی نیستند ولی بسیاری از معامله گران از آنها نیز استفاده میکنند.
این اعداد نشان دهنده این است که قیمت پس از یک حرکت قیمت دیگر میتواند تا کجا به پیش رود. به عنوان مثال، اگر سهام از 1 واحد به 2 واحد برسد، میتوان اعداد فیبوناچی را برای آن اعمال کرد. سقوط قیمت نیز میتواند به 1٫76 واحد باشد که در این حالت 23٫6٪ اصلاح قیمت رخ داده است. در نمودار زیر، خطوط مربوط به نمودار ارزش سهام رسم شده که به آنها خطوط حمایت، خط بازگشت و ... میگویند.
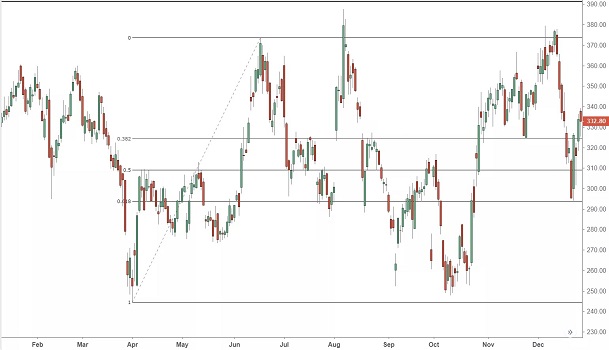
برای آشنایی بیشتر با موضوع استفاده از اعداد فیبوناچی در بازارهای مالی پیشنهاد میشود که آموزش فیبوناچی در تحلیل تکنیکال بورس | به زبان ساده از مجله فرادرس را مطالعه کنید. همچنین یک فیلم آموزشی از فرادرس نیز برای آشنایی با شاخصها یا اندیکاتورهای بازار بورس در ادامه معرفی شده است.
تحلیل تکنیکال (Technical Analysis) در بازار سرمایه اغلب به صورت خودکار و به کمک نشانگر یا اندیکاتورهایی قابل اجرا است. از آنجایی که یکی از رایجترین اندیکاتورهای بازارهای مالی، اندیکاتور (MACD (Moving Average Convergence Divergence است این آموزش از فرادرس به این گروه از نشانگرهای مالی میپردازد در این بین آموزش پیشرو به اعداد طلایی و دنباله فیبوناچی و نقش آن در پیشبینی بازارهای مالی اهمیت ویژهای داده و به عنوان یکی از درسها به مفهوم واگرایی و همگرایی سری فیبوناچی پرداخته است.
بحث میانگین متحرک (Moving Average) که یکی از موضوعات مربوط به سری زمانی است و امکان هموارسازی دنباله را دارد در این فرادرس، آموخته شده و روشهای مختلف آن مورد بحث و بررسی قرار گرفته است. فهرست سرفصلها و رئوس مطالب مطرح شده در این مجموعه آموزشی، در ادامه آمده است.
- درس یکم: مقدمهای بر اندیکاتور MACD
- درس دوم: مروری بر مفاهیم مقدماتی تحلیل تکنیکال
- درس سوم: اندیکاتورها
- درس چهارم: واگرایی معمولی
- درس پنجم: واگرایی مخفی
- درس ششم: واگرایی زمانی
- درس هفتم: نمونههای معاملاتی بازار ایران
این آموزش برای علاقهمندان به بورس و بازارهای مالی مفید بوده و کاربردهای زیادی دارد. زمان این آموزش ۴ ساعت و ۲۳ دقیقه بوده و در هفت درس منتشر شده است.
خلاصه و جمعبندی
همانطور که در متن خواندید، اعداد فیبوناچی، الگوی فیبوناچی یا سری فیبوناچی، دارای ویژگیهای خاصی است که آن را نسبت به سریهای دیگر در ریاضیات متمایز میکند. از طرفی کاربردهای آن در بورس اوراق بهادار و بازارهای مالی به وفور دیده میشود، بطوری که یک روش برای پیشبینی آینده چنین بازارهایی محسوب میشود. از نظر هندسی و تناسب شکلها و اجسام در طبیعت نیز از نسبت اعداد فیبوناچی که همان اعداد طلایی است الهام گرفته میشود. مجسمهسازها، نقاشها شاید به طور ناخودگاه از این تناسب برای ایجاد مجسمه یا تابلوهای نقاشی بهره میبرند. هر چند آگاهی از علم ریاضیات و اعداد کار سختی به نظر میبرسد ولی همواره به یاد داشته باشیم که این علم به منظور بیان ویژگیها و پدیدههای طبیعی بوجود آمده و همین امر به زیبایی ریاضی و درک عملکرد آن میافزاید.











سلام.عالی و کاربردی .با ارزوی توفیق روزافزون.منتظر امزش های بعدی شما هستم.با تشکرو احترام فراوان
ممنون از شما
سلام
وقت بخیر
در همه جا نوشته که نسبت طلایی برابر است با ۱.۶۱۸۰۳۳ و… اما کتابی را مطالعه میکنم که تاکید دارد نسبت طلایی برابر است با ۰.۶۱۸ ، بالاخره ۱.۶۱۸ است یا ۰.۶۱۸ ؟
در قسمتی هم میگوید اگر عدد ۰.۶۱۸ را در هر یک از اعداد ضرب کنید، عدد ماقبل را بدست میآورید در صورتی که اکثر حاصل بدست آمده تقریبا نزدیک است به عدد ماقبل و دقیقا خود آن عدد نیست. مثلا ۱.۸۵۴=۰.۶۱۷×۳
ممنون میشم در این دو سوال من را راهنمایی کنید.
با احترام
با سلام؛
نسبت طلایی و دنبالههای بعد از آن همگی با عدد ۱٫۶۱۸۰۳۳۹۸۸۷۵ تعریف میشوند.
با تشکر از همراهی شما با مجله فرادرس
عالی و بسیار کاربردی
متشکرم