جایگشت و ترکیب — به زبان ساده

اغلب افراد معمولاً جایگشت و ترکیبِ اعداد را با همدیگر اشتباه میگیرند و نمیدانند که هر یک به چه معنا است. در این نوشته روش آسانی برای بهخاطرسپاری کارکرد هر کدام از این مفاهیم ارائه میدهیم. جایگشت به نظر پیچیده میآید و در واقعیت هم چنین است. وقتی از جایگشت صحبت میکنیم، هر گونه جزییاتی هر چند کوچک اهمیت دارند. «آلیس، باب و چارلی» با «چارلی، باب و آلیس» متفاوت است!
از طرفی ترکیب بسیار سادهتر است و در آن جزییات اهمیتی ندارند. در این زمینه تفاوتی بین «آلیس، باب و چارلی» با «چارلی، باب و آلیس» وجود ندارد. بدین ترتیب جایگشتها در مورد لیستها به کار میروند و ترتیب در مورد آنها مهم است؛ در حالی که ترکیبها در مورد گروهها کاربرد دارند و ترتیب هیچ اهمیتی ندارد. در این مطلب از مجله فرادرس با تعریف جایگشت و ترکیب و تفاوت آنها با یکدیگر آشنا میشویم.
جایگشت
در ابتدا مفهوم جایگشت را بررسی میکنیم. جایگشت به معنی پیدا کردن تمامی روشهای ممکن برای انجام یک کار است. به این دلیل از واژه جذاب جایگشت استفاده میکنیم که قرار است در مورد همه جزییات دقیق باشیم و این جزییات شامل ترتیب همه آیتمها نیز میشود.
فرض کنید 8 نفر وجود دارند:
- آلیس (Alice)
- باب (Bob)
- چارلی (Charlie)
- دیوید (David)
- حوا (Eve)
- فرانک (Frank)
- جرج (George)
- هوراسیو (Horatio)
چند روش برای اهدای جوایز مقام اول، دوم و سوم بین این هشت نفر وجود دارد؟
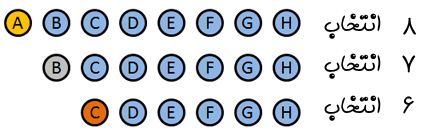
در این جا باید از جایگشت استفاده کنیم، چون ترتیب اهدای این مدالها مهم هستند. روش کار به صورت زیر است:
- مدال طلا: 8 گزینه به صورت A B C D E F G H وجود دارد. (حالا دلیل انتخاب این اسامی را متوجه شدهاید.) A یا آلیس مدال طلا را میبرد.
- مدال نقره: 7 گزینه به صورت B C D E F G H وجود دارد. فرض میکنیم B یعنی باب مدال طلا را ببرد.
- مدال برنز: 6 گزینه به صورت C D E F G H وجود دارد. فرض کنید C یعنی چارلی مدال برنز را ببرد.
گرچه ما افراد معینی را برای دریافت مدالها انتخاب کردیم، اما مهم نیست این افراد چه کسانی باشند. ما در ابتدا هشت گزینه داریم، سپس 7 گزینه و در نهایت 6 گزینه، پس مجموع تعداد گزینهها برابر با 336 = 8 × 7 × 6 است.
توضیح بیشتر
اینک نگاهی به جزییات میاندازیم. ما باید سه نفر را از میان 7 نفر انتخاب کنیم. برای انجام این کار با همه گزینهها (8) آغاز میکنیم و هر بار یکی از آنها را انتخاب میکنیم (7 و سپس 6) تا این که همه مدالها اهدا شده باشند.
میدانیم که فاکتوریل 8 به صورت زیر است:
1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 =!8
متأسفانه این محاسبه با نتایج ما همخوانی ندارد. ما چگونه میتوانیم فاکتوریل را در عدد 5 متوقف کنیم؟ این همان جایی است که جایگشت به کار میآید. چگونه میتوانیم از شر حاصلضرب 1 × 2 × 3 × 4 × 5 خلاص شویم؟ میدانیم که این مقدار برابر با !5 است. بنابراین اگر !8 را بر !5 تقسیم کنیم، نتیجه مطلوب حاصل میشود:
و اگر بپرسید چرا از عدد 5 استفاده کردیم، باید بگوییم چون این تعداد افرادی است که پس از دریافت مدالها باقی میمانند، 3 نفر مدال میگیرند و 5 نفر بدون مدال باقی میمانند. بنابراین یک روش بهتر برای نوشتن عبارت فوق به صورت زیر است:
عبارت فوق تنها یک روش جذاب برای گفتن این است که «از 3 عدد نخست، از 8 تا استفاده کن». اگر در مجموع n آیتم داشته باشیم و بخواهیم k تا را با ترتیب خاصی از میان آنها انتخاب کنیم، فرمول کلی به صورت زیر خواهد بود:
این همان فرمول جذاب جایگشت است. n آیتم داریم و میخواهیم تعداد روشهایی که میتوان k آیتم را از میان آنها با ترتیب معین انتخاب کرد، به دست آوریم:
ترکیب
ترکیبها نسبت به جایگشت سادهتر هستند. در این مورد ترتیب اهمیتی ندارد. میتوانید آیتمها را با هم مخلوط کنید و نتیجه یکسان خواهد بود. فرض کنید بودجه محدودی داریم و نمیتوانیم مدالهای جداگانه طلا، نقره و برنز اهدا کنیم. در واقع بودجه ما صرفاً کفاف قوطیهای حلبی خالی را میدهد!
به چند روش میتوان 3 قوطی حلبی را به 8 نفر اهدا کرد؟
در این مورد ترتیبی که افراد را انتخاب میکنیم اهمیتی ندارد. اگر یک قوطی را به آلیس بدهیم، یک قوطی به باب و یکی هم به چارلی بدهیم، هیچ فرقی ندارد با این که اول قوطی را به چارلی بدهیم، بعد به آبی و در نهایت به آلیس. در هر صورت قوطیها به طور یکسانی توزیع میشوند.
کسر افزونگیها
در این جا نکته جالبی پیش میآید. در واقع افزونگیهایی وجود دارند: آلیس باب چارلی = چارلی باب آلیس. اینک برای لحظهای اجازه بدهید ببینیم به چند طریق میتوانیم این 3 نفر را بازآرایی کنیم؟ ما 3 انتخاب برای نفر اول، 2 انتخاب برای نفر دوم و 1 انتخاب برای نفر سوم داریم. بنابراین بازآرایی 3 نفر اول به 1 × 2 × 3 روش امکانپذیر است.
لحظهای صبر کنید، اما این شبیه همان جایگشت است. در واقعیت هم چنین است. اگر N نفر داشته باشیم و بخواهیم بدانیم برای همه آنها چند بازآرایی وجود دارد، این تعداد برابر با N فاکتوریل (!N) خواهد بود.
بنابراین اگر 3 قوطی حلبی داشته باشیم که بخواهیم آنها را اهدا کنیم، !3 یا 6 روش برای هر انتخاب وجود دارد. اگر بخواهیم بدانیم که چه تعداد ترکیب داریم، میبایست همه جایگشتها را محاسبه کنیم و آن را بر همه موارد تکراری تقسیم کنیم. در این مورد ما قبلاً حساب کردیم که 336 جایگشت داریم و میخواهیم بر 6 افزونگی برای هر جایگشت تقسیم کنیم، بنابراین 336/6 = 56.
نهایتا فرمول کلی ترکیب به صورت زیر بیان میشود:
یعنی «همه روشهایی که میتوان k نفر را از میان n نفر انتخاب کرد را پیدا کن و آن را بر !K تقسیم کن.» با نوشتن این عبارت، «فرمول ترکیب» یا تعداد روشهای ترکیب K آیتم از مجموعه n شیء را به دست میآوریم:
برخی اوقات (c(n,k به صورت زیر نیز نوشته میشود:
که ضریب دوجملهای نام دارد.
چند مثال
در ادامه چند مثال از جایگشت (که ترتیب اهمیت دارد) و ترکیب (که ترتیب اهمیتی ندارد) را ارائه کردهایم:
- ترکیب: انتخاب تیمی 3 نفره از گروهی متشکل از 10 نفر. C(10,3) = 10!/(7! × 3!) = 10 × 9 × 8 / (3 × 2 × 1) = 120
- جایگشت: انتخاب یک رئیس، نایبرئیس و معاون از گروهی 10 نفره. P(10,3) = 10!/7! = 10 × 9 × 8 = 720
- ترکیب: انتخاب 3 دسر از منویی که 10 آیتم دارد: C(10,3) = 120
- جایگشت: فهرست بندی 3 مورد از دسرهای مورد علاقه با ترتیب اولویت از منویی حاوی 10 آیتم.
در این مطلب از مجله فرادرس با تعریف ترکیب و جایگشت آشنا شدیم. توصیه میکنیم که صرفاً به حفظ کردن فرمولها نپردازید و تلاش کنید طرز کار آنها را یاد بگیرید. ترکیب سادهتر از جایگشت به نظر میرسد و در واقعیت نیز چنین است. همیشه تعداد ترکیبها کمتر از جایگشتها هستند.


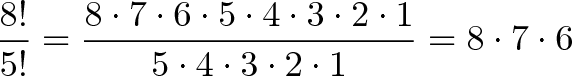
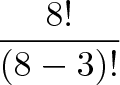
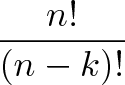
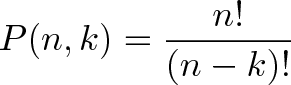
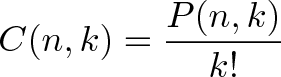
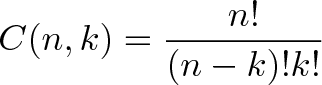
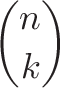












مثال مدال و قوطی حلبی عالی بود من بعد از کلی خوندن با این مثال تازه متوجه مطلب شدم، ممنون از شما:)
سلام ، یک سوال :شخصی از هر کدام از سکه های یک،دو،سه،چهار،پنج،شش،هفت،هشت،نه و ده هزار تومانی،یک عدد دارد به چند روش می توان این ده سکه را بین 3 نفر تقسیم کرد ؟که مجموع هر گروه یکسان باشد
از عدد یک تا چهل ونه چند عدد شش رقمی مختلف میشه نوشت ؟؟؟مثلا با دو عدد چهار عدد مختلف میشه نوشت و با سه عدد نه عدد مختلف میشه نوشت که فکر کنم فرمولش برای دو مثالی که نوشتم اعداد عدد به توان خودش منهای یک یا بعلاوه یک باشه یعنی در هر عدد به توان خودش (منها یا بعلاوه یک ) تعداد اعداد متفاوت و میشه مشخص کرد اما اگر از بین این اعداد تعداد محدودی لازم باشد چی ؟؟مثلا با چهل و نه عدد میشه چهل و نه به توان چهل ونه عدد نوشت (اعداد چهل و نه رقمی منظورم است )ولی اگر تعداد اعداد شش رقمی و از بینشون مشخص کنیم چند عدد ممکنه نوشت ؟؟؟امیدوارم درست توضیح داده باشم
سلام شما میخواین یک عدد ۶ رقمی بسازید با رقم های متفاوت پس میتونم بگم ک شما تو ی جایگاه نمیتونی دو عدد بزاری از نظر من شما این عدد ۶ رقمی رو بازم باید از بین اعداد ۱_۹انتخاب کنید و ب همون ترتیب فاکتوریل از ۹ تا ۴ پیش برید .اگ اشتباه شرمنده
سلام هفت کشور که هرکدام سه تیم راهی مسابقات کردن تعداد حالت هایی که میتوان به گروه هفت تیمی درست کردکه دو تیم ازیه کشور در گروه هفت تیمی نباشد
ترکیب ۱ از ۳ کلا به توان ۷
میشه 3⁷
بسیار عالی، ممنون
بسیار عالی
ازبین ۹لامپ ۳لامپ معیوب است انتخاب ۴لامپ که ۲عدد معیوب و۲عدد سالم به چند روش،ممکن است؟
سلام ودرود
۱۰ نقطه روی دایره داریم برای کشیدن وتر میشود
C(10,2)
؟
سلام
عالی
ممنون از شما
در این قسمت
ترکیب: انتخاب تیمی 3 نفره از گروهی متشکل از 10 نفر. C(10,3) = 10!/(7! × 3!) = 10 × 9 × 8 / (3 × 2 × 1) = 120
7! از کجا آمده ؟
7 تعداد ایتم های است که انتخاب نکردیم
سلام و وقت بخیر دوست عزیز؛
چنان که در تصویر ماقبل آخر این نوشته نیز اشاره شده است، برای محاسبه ترکیب k=3 از n=10 مقدار 10! را بر حاصلضرب k! در (n-k)! یعنی 7! تقسیم میکنیم. این 7! که اشاره کردید نتیجه تفریق 3 از 10 است.
از توجه و همراهی شما با مجله فرادرس سپاسگزاریم.
خوب ومفید
سه نفر زن و نه نفر مرد را میخواهیم به گروه های سه نفری و چهار نفری و پنج نفری تقسیم کنسم بطوریکه در هر گروه یک زن باشد.به پند طریق امکان این کار هست؟
یک خانواده سه نفری پنج شنبه یا جمعه متولد شده اند .احتمال اینکه هم پنج شنبه و هم جمعه تولد بگیرند چقدر است؟ یک بار سه نفر را عیر متمایز و یک بار هم متمایز بگیرید
ممنون میشم کمکم کنید دو روز هست وقت منو گرفته اخر هم موفق نشدم
سلام ممنون میشم بهم کمک کنید
با ارقام 0,2,3,4,6,8,9 یک عدد چها رقمی بدون تکرار میسازیم احتمال اینکه عدد حاصل بر 4 بخش پذیر باشد کدام است ؟
بسیار عالی… اینکه در پایان سعی کردید با مثال تفاوتهاشون رو بیان کنید به نظرم بسیار کار رو تکمیل تر کرد. سپاسگزارم.
سلام
ممنون میشوم اگر برای حل این مسئله به من کمک کنید
سه گروه داریم که هر گروه شامل 11 عدد مشابه به شرح می باشد
( 0 و 0.1 و 0.2 و 0.3 و 0.4 و 0.5 و 0.6 و 0.7 و 0.8 و 0.9 و 1 ) =a
( 0 و 0.1 و 0.2 و 0.3 و 0.4 و 0.5 و 0.6 و 0.7 و 0.8 و 0.9 و 1 ) =b
( 0 و 0.1 و 0.2 و 0.3 و 0.4 و 0.5 و 0.6 و 0.7 و 0.8 و 0.9 و 1 ) =c
به چند حالت می توان یک گروه سه عضوی ساخت به طوری که در هر گروه ساخته شده مجموع اعداد برابر یک شود و همچنین ترتیب هم مهم است.
یعنی (0.2و0.3و0.5) و (0.3و0.2و0.5) دو حالت مختلف هستند
با تشکر
با سلام.
ببینید شما برای عدد اول یا باید صفر بگذارید یا ۰.۱ یا …. تا ۱ ( که میشه یازده تا) حالا تک تک میریم جلو. اگه عدد اول رو صفر بگذارم در واقع صفر را تثبیت کردم و می خوام روی دو تا عدد بعدی بحث کنم که میشه یازده احتمال= (۰،۱،۰) (۰,۰.۹,۰.۱)… الی آخر. خب حالا میخوام عدد اول رو ۰.۱ بگذارم. الآن احتمال یکی کم میشه= ۱۰ احتمال( چون دیگه یک نمی تونی بذاری. اگه یک بذاری که جمعش بیشتر از یک میشه) عدد بعدی ۰.۲ که میشه ۹ تا. همین جور باید ادامه بدیم تا ۰.۹.( ۰.۹ دو تا احتمال داره. پس باید از یازده جمع کنیم تا دو.) اما ما یک هم داریم. یعنی یک رو هم می تونم رقم اول در نظر بگیرم. که اگه یک اول باشه یک حالت بیشتر به وجود نمیاد= ۱,۰,۰. خب پس حالا باید از یازده تا یک جمع کنی= ۱۱+۱۰+۹+…+۱= ۶۶.
سلام اگه ۳تا انتخاب از n تا داشته باشیم که برابر ۳۵ شده ، n چند بوده ؟
سلام وقت شما بخیر؛
به یاد دارید که فرمول مربوط به ترکیب ۳ شي از n شي به صورت (3n) است. پس از ساده سازی و استفاده از طرفین وسطین به رابطه زیر خواهیم رسید.
n (n-1) (n-2) = 35 * 6
که یک معادله درجه ۳ است و حل آن مشکل به نظر می رسد. ولی می توان برای پیدا کردن پاسخ، سه عدد دنبال هم را در نظر بگیریم که حاصل ضرب آنها برابر با ۲۱۰ (یعنی حاصل ضرب ۳۵ و ۶) باشد. با کمی سعی و خطا به اعداد ۵ و ۶و ۷و می رسید که مشخص می شود مقدار n= 7 است.
برای آگاهی از نحوه حل چنین معادلاتی بهتر است حل معادله درجه ۳ — به زبان ساده را مشاهده کنید.
پیروز و موفق باشید.
با سلام در یک آپارتمان هشت طبقه آسانسور فقط در طبقات فرد میایستد اگر ۷نفر در آسانسور باشند به چند طریق می توانند از آسانسور پیاده شوند
در یک مسابقه لاتاری شش عدد باید از بین چهل و نه عدد انتخاب شود چند جواب (هر شش عدد را یک جواب فرض میکنیم ) میتوان تعیین کرد ؟؟؟امیدوارم درست توضیح داده باشمد
خیلی ساده و روان آموزش دادید. سپاس
چه تعداد جایگشت های حروف کلمه summit شامل یکی از الگو های it و sum میباشد؟
خودتو گیج نگن و به جای پیاده شدن از یه واژه دیگه استفاده کن
فکر کن ۴ تا طبقه هست یک سه پنج هفت
که میخوای بدیشون به ۷ نفر
حالا ترتیب هم مهم نیست همه طبقهدها مثل همه
پس ترکیب ۷ از ۴ ، ۳۵ حالت میشه
البته مطمین نیستم
برای هر نفر ۴ انتخاب وجود داره با این حساب فکر میکنم بشه چهار بتوان هفت حالت
بسیار عالی. سالم باشید
سلام ما سه گروه داریم که این سه گروه هر کدوم سه عضو دارن میخوایم یه گروه سه عضوی با این اعضا بسازیم به چند حالت میتونیم؟ اینجا باید از ترکیب استفاده کرد؟ ترتیب قرار گیری اعضا مهم نیست ولی مثلا عضو اول از گروه اول با عضو اول از گروه دوم و عضو اول از گروه سوم میشه یک انتخاب؛ عضو اول از گروه اول با عضو اول از گروه دوم و عضو دوم از گروه سوم میشه یه انتخاب دیگه و به همین ترتیب. چطور باید حل کرد؟
سلام به نظر من زیاد سخت نیست و میشه به راحتی این رو حل کرد
اول اینکه با خودت فکر کن که از گروه اول سه انتخاب و از گروه دوم و سوم هم هر کدوم سه انتخاب داریم . که تعداد حالت های ممکن میشه 27 حالت
همین رو از راه ترکیب هم میشه انجام داد و به جواب رسید
مرسی از شما
من از درس چیزی نمی فهمیدم ولی خداروشکر با توضیح شما فهمیدم ممنونم
سلام ما سه گروه داریم که این سه گروه هر کدوم سه عضو دارن میخوایم یه گروه سه عضوی با این اعضا بسازیم به چند حالت میتونیم اینجا باید از ترکیب استفاده کرد؟ ترتیب قرار گیری اعضا مهم نیست ولی مثلا اینکه عضو اول از گروه اول با عضو اول از گروه دوم و عضو اول از گروه سوم مثلا میشه یک انتخاب. عضو اول از گروه اول با عضو اول از گروه دوم و عضو دوم از گروه سوم میشه یه انتخاب دیگه و به همین ترتیب. چطور باید حل کرد؟
سلام
خیلی ممنون از توضیحات خوبتون.
یه تست هست که من نمیتونم حلش کنم…اگه کمکم کنین ممنون میشم.
توی یک لیگ ۱۶ تیم وجود دارند.چه تعداد حالت وجود دارد که تیم B بین دو تیم A و C قرار گیرد؟
سلام,من این سوال رو حل کردم اما ممکنه که اشتباه باشه!اگر اشتباه بود بنده رو ببخشد!
بسته ABC رو بساز (در نظر بگیر این 3 تیم یک تیم واحد هستند) یعنی به جای 16 تا تیم حالا 14 تا تیم وجود داره. حالا اول در نظر بگیر این بسته ABC یا همون 3 تا تیممون که ادغام کردیم به همراه 13 تیم دیگر در چند جایگاه میتواند قرار بگیره؟14! چون 14 تا تیم هستن در کل!سوال بعد اینه که در بسته ABC (یا همون تیم ترکیب شده از سه تیممون) در وسطش(تیم B) چند جایگاه میتونه قرار بگیره؟12 تا جایگاه چون توی جدول فرضی از تیم ها که هستن 14 تا تیم وجود داره که منهای دو تیم A و B که نمیتوانند در جای B باشند(تیم تکراری که وجود نداره!) 12 تیم وجود داره که میتونیم B در نظر بگیریمشون. سپس این اعداد رو ضرب در 2 میکنیم چون تیم ادغام شدمون یا همون بسته ABC دارای حالت CBA هم هست به این معنی که جای A و C میتواند عوض شود!پس تا اینجا اعدادمون که باید در هم ضرب شوند عبارتند از !14- 2 – 12 که همه باید در هم ضرب بشوند!
یادآوردی:14! برای حالات 14 تیم بود 12 برای تیم هایی که میتوانند جای B باشند و 2 برای جابجایی A و C که در نهایت میشود ! 2X12X14 که مساوی است با یه عدد خیلی گنده!(ازتون نمیخوان)!….
امیدوارم که اشتباه حل نکرده باشم! اما به هر حال منم دانش آموزم و پر از اشتباه!
جایگشت اینکه در یک صف 7 نفره 2 تا مرد 3 تا زن 2تامرد کنار هم باشه رو چطور حساب می کنند
جواب میشه
!2*!14
( ترکیب 3 از 16 ) * 14! * 2!
عالی بود
ممنونم از شما
خواستم بعد از بیش از 30 سال این درس را مرور کنم
در اون سالها به جایگشت تبدیل هم میگفتن
با سلام و وقت بخیر
چطور باید این را ثابت کرد؟
انتخاب با جایگذاری و بدون رعایت ترتیب
فرمولش هست: r تا از n+r-1
سلام و درود بر شما خواننده گرامی،
در یکی دیگر از نوشتارهای مجله فرادرس به نام متغیر تصادفی و توزیع دو جمله ای منفی — به زبان ساده این موضوع مشخص و توضیح داده شده است.
از این که همراه مجله فرادرس هستید، سپاسگزاریم.
شاد و تندرست و پیروز باشید.
بسیار عالی و جذاب و روان
مرسی استاد عزیز
خیلی عالی بود یک ساعت به جزوه نیگاه کردم هیچی نمیفهنیدم . خوب توزیح دادین .
عالی بود ممنون از شما
با سلام و احترام
یه سوالی داشتم
اگر شرکتی بیمه ای بخواهد برای بیمه شدگان کدی انتخاب کند که از ۴ حرف فارسی و یک شماره ۵ رقمی تشکیل شده به چند بیمه شده می تواند کد دهد?
O my god, o my god, o my god.
عاااااااااااااااااااااااااااااااااااااااااااااالی بود عااااااااااااااااااااااااااااااالی بود. نمیدونم چطوری تشکر کنم.
ﻋﺎﻟﯽ ﺑﻮﺩ ﻣﻤﻨﻮﻥ ﺍﺯ ﻧﻮﻳﺴﻨﺪﻩ و ﺳﺎﻳﺖ ﻓﺮﺍﺩﺭﺱ
سلام
۹ توپ شامل ۳ توپ از سه رنگ قرمز ک زرد و ابی داریم بین ۳ نفر تصادفی تقسیم کنیم احتمال اینکه هرکدوم از سه رنگ داشته باشن چنده؟
دمتون گرم
صد هزار تومان رو به چند روش میشود با پول های 1000 و 2000 و 5000 و 10000 نوشت!؟ لطفت با فرمول بنویسید ممنون