تبدیل فوریه (Fourier Transform) و محاسبه آن — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

در مطالب قبلی وبلاگ فرادرس آموختیم که سری فوریه، روشی برای بیان یک تابع به صورت چندین موج سینوسی و کسینوسی است. در این مطلب تبدیل فوریه مورد مطالعه قرار میگیرد. تبدیل فوریه یک ابزار ریاضی است که شکل موج معلوم را به شکلهای دلخواه تبدیل میکند. در واقع تبدیل فوریه، یک تابع یا سیگنال در حوزه زمان را به حوزه فرکانس انتقال میدهد.
در این مطلب، ابتدا مفهوم تبدیل فوریه و روابط حاکم بر آن به صورت دقیق مورد مطالعه قرار میگیرد. در ادامه، تبدیل فوریه چند تابع خاص با جزئیات بررسی میشوند و در نهایت برای سادگی محاسبه تبدیلات فوریه در توابع مختلف، ویژگیهای گوناگون این تبدیلات مورد مطالعه قرار میگیرند. پیشنهاد میشود قبل از مطالعه این مطلب، مبحث توابع متعامد را مطالعه فرمایید.
مقدمهای بر تبدیل فوریه
هر چیزی که به صورت تابعی از زمان، مکان و یا متغیرهای دیگر باشد را میتوان با استفاده از یک شکل موج مورد مطالعه قرار داد. برای مثال میتوان به امواج صوتی و میدانهای مغناطیسی اشاره کرد. همچنین ارتفاع یک تپه بر حسب موقعیت و موجودی انبار شما را نیز میتوان به صورت یک شکل موج نمایش داد. تبدیل فوریه به ما ابزار قدرتمندی برای بررسی این شکل موجها ارائه میدهد.
تبدیل فوریه، کاربرد بسیار زیادی در ریاضیات، مهندسی و علم فیزیک دارد. یکی از شاخههای تبدیل فوریه، «تبدیل فوریه گسسته» (Discrete Fourier Transform) است که به صورت اختصاری با نماد DFT نمایش داده میشود. این عملگر به صورت رایج با استفاده از «تبدیل فوریه سریع» (Fast Fourier Transform) قابل محاسبه است. تبدیل فوریه سریع به صورت اختصاری با نماد FFT نمایش داده میشود. پیدایش مفهوم FFT باعث پیشرفت بسیار زیاد در علم الکترونیک و مهندسی برق نیز شده است.
تبدیل فوریه یک تابع با نماد (f(x که میتواند شامل اعداد حقیقی و مختلط باشد را با نماد (F(s نمایش میدهند، که یک فرایند برگشت پذیر است. توجه کنید که در اینجا حاصل ضرب x و s عبارتی بیبعد خواهد بود و به طور معمول x زمان در نظر گرفته میشود (بنابراین تابع f، نشان دهنده سیگنال در حوزه زمان است) و s معکوس زمان و یا فرکانس (در این حالت F نشان دهنده سیگنال در حوزه فرکانس است) را نشان میدهد.
تبدیل فوریه تابع (f(x با استفاده از رابطه زیر تعریف میشود.
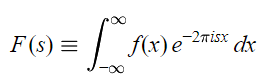
همانطور که اشاره شد تبدیل فوریه یک فرایند برگشت پذیر است، بنابراین در صورتی که تبدیل فوریه یک تابع را داشته باشیم و خود تابع مجهول باشد، از رابطه زیر برای محاسبه تابع مجهول میتوان استفاده کرد. این رابطه به تبدیل فوریه معکوس معروف است.
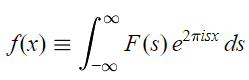
در عبارت بالا i با استفاده از رابطه زیر تعریف میشود.
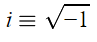
عبارت نمایی مختلط موجود در تبدیل فوریه، مهمترین بخش تبدیل فوریه است. این عبارت عدد مختلطی را نشان میدهد که قسمت حقیقی و موهومی آن، یک تابع نوسانی است و با استفاده از «فرمول اویلر» (Euler's Formula) به شکل زیر نمایش داده میشود.
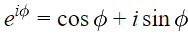
برای مثال در صورتی که در رابطه فوق، برابر با باشد، فرمول اویلر به شکل زیر بازنویسی خواهد شد.
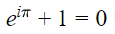
انجام محاسبات با استفاده از توابع مختلط نمایی، بسیار راحت تر از انجام محاسبات روی توابع مثلثاتی است. نکته دیگر این است که نمایش توابع نمایی بسیار کوتاهتر و سادهتر از توابع مثلثاتی به نظر میرسد و بیان عبارت تبدیل فوریه با استفاده از آن، به سادهترین شکل ممکن انجام شده است.

تبدیل فوریه گسسته
تبدیل فوریه پیوسته، یک سیگنال در حوزه زمان در بازه نامحدودی را به یک طیف پیوسته تبدیل میکند که از تعداد نامحدودی تابع سینوسی تشکیل شده است. در برخی از علوم، با سیگنالهایی در تماس هستیم که به صورت گسسته و در بازه محدودی به وجود آمدهاند. در این حالت، تنها تعداد محدودی از توابع سینوسی برای تبدیل این سیگنال مورد نیاز است و در این گونه مسائل تبدیل فوریه گسسته کاربرد بسیار زیادی دارد.
همانطور که اشاره شد، تبدیل فوریه گسسته به صورت اختصاری با نماد DFT نمایش داده میشود. در صورتی که N داده یکنواخت به فرم xj داشته باشیم که در آن، j از 0 تا N-1 تغییر میکند، تبدیل فوریه گسسته این دادهها به شکل زیر نمایش داده میشود.
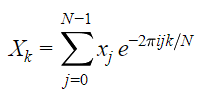
تبدیل فوریه معکوس این دادههای گسسته نیز به شکل زیر قابل محاسبه است.
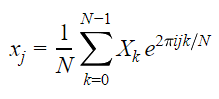
در این دو رابطه، متغیر پیوسته s با متغیر گسسته k عوض شده است. بنابراین از رابطه بالا نتیجه میشود که اگر تبدیل فوریه گسسته روی تعداد N ورودی در حوزه زمان اعمال شود، خروجی آن به صورت طیف فرکانس شامل N نقطه با فرکانس و دامنه معلوم خواهد بود.
محدوده فرکانس (k) بین (N/2 - 1)- و N/2 نیز میتواند تغییر کند. خروجی این تبدیل فوریه گسسته، به فرم یک دامنه Ak و یک فاز Φk خواهد بود. بنابراین هر متغیر گسسته خروجی این تبدیل را میتوان به صورت خلاصه مطابق با رابطه زیر نمایش داد.
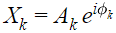
تبدیل فوریه گسسته هیچ اطلاعاتی را از سیستم حذف نمیکند و اطلاعاتی را نیز به آن نمیافزاید.
تبدیل فوریه گسسته در مطالعات مختلف به صورت رایج با یک الگوریتم معروف به نام تبدیل فوریه سریع محاسبه میشود. همانطور که بیان شد، الگوریتم تبدیل فوریه سریع را به صورت خلاصه با نماد FFT نمایش میدهند. این الگوریتم اولین بار توسط «گاوس» (Gauss) در سال 1805 به وجود آمد ولی استفاده از آن به شکل رایج، اولین بار در سال 1965 در تحقیقات James W. Cooley و John W. Tukey مشاهده شده است. روش FFT نسبت به روش DFT پیچیدگی و خطای کمتری دارد.
تبدیلات پایه
تبدیلات فوریه پایه در شکل زیر به تصویر کشیده شدهاند. با ترکیب این تبدیلات و بررسی قوانین حاکم بر آنها میتوان تبدیلات فوریه برای توابع مختلف را مورد بررسی قرار داد.
تبدیل فوریه تابع ثابت
در صورتی که تابع ثابتی به فرم 1=(f(x داشته باشیم. تبدیل فوریه آن به شکل زیر در خواهد آمد.
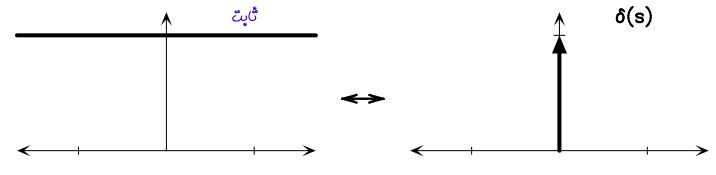
شکل سمت چپ، تابع 1=(f(x را نشان میدهد و شکل سمت راست تبدیل فوریه آن را به تصویر کشیده است. همانطور که مشاهده میشود، تبدیل فوریه تابع ثابت ۱ برابر با تابع دلتای دیراک است. این تابع فقط در 0=x مقداری برابر با بینهایت دارد و در باقی نقاط، اندازه آن صفر است.

تبدیل فوریه تابع Boxcar
فرض کنید که یک تابع Boxcar داشته باشیم، در این صورت تابع مورد نظر با استفاده از رابطه زیر تعریف میشود.
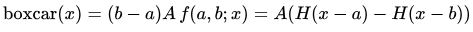
این رابطه نشان میدهد که تابع مربوطه تنها در بازه مشخصی، مقداری ثابت دارد و در باقی نقاط، مقدار این تابع برابر با صفر است. تبدیل فوریه این تابع به شکل زیر محاسبه خواهد شد.
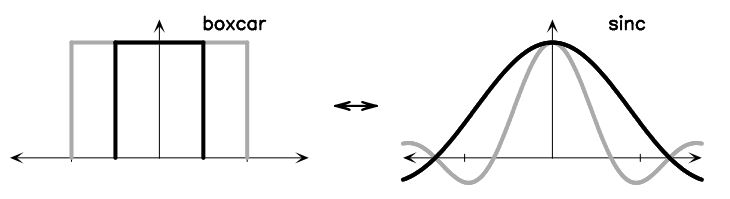
دو تابع مختلف Boxcar در سمت چپ تصویر فوق نشان داده شدهاند. تبدیل فوریه این دو تابع در سمت راست شکل بالا نشان داده شده است. مشاهده میشود که تبدیل فوریه یک تابع Boxcar برابر با «تابع سینک» (Sink Function) است. رابطه تابع سینک به صورت کلی مطابق با معادله زیر بیان میشود.
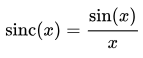
همانطور که مشاهده میشود، هرچه تابع Boxcar عریض تر باشد، تبدیل فوریه آن در نزدیکی محور مختصات نازک تر میشود.
تبدیل فوریه تابع مثلثی
در این قسمت تبدیل فوریه یک «تابع مثلثی» (Triangle Function) مورد بررسی قرار میگیرد. تابع مثلثی، تابعی است که در محدوده خاصی، مقدار دارد و مقدار این تابع در خارج از این محدوده، برابر با صفر در نظر گرفته میشود. برای مثال، رابطه یک تابع مثلثی به شکل زیر قابل نمایش است.
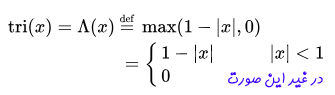
شکل زیر تبدیل فوریه یک تابع مثلثی را نشان میدهد.
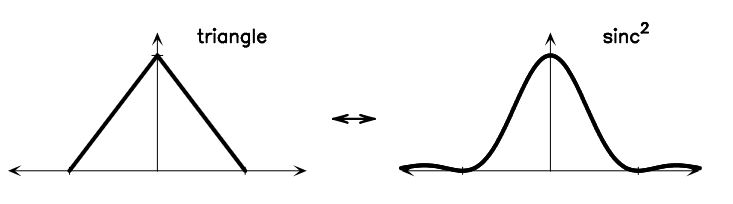
در شکل بالا، نمودار سمت چپ، تابع مثلثی را نشان میدهد و نمودار سمت راست تبدیل فوریه تابع مذکور را به تصویر کشیده است. همانطور که مشاهده میشود گوشههای مثلث با استفاده از تبدیل فوریه به منحنی تبدیل شده است و این موضع کاربرد بسیار زیادی در تحلیل مسائل مختلف دارد.
نکته دیگر این است که تبدیل فوریه یک تابع مثلثی به شکل مجذور تابع سینک بیان میشود. همانطور که در قسمت قبل بیان شد، تابع سینک برابر با حاصل تقسیم سینوس یک عبارت تقسیم بر خود آن عبارت است.

تبدیل فوریه تابع گاوسی (توزیع طبیعی)
در این قسمت، تبدیل فوریه یک «تابع گوسی» (Gaussian Function) مورد بررسی قرار میگیرد. تابع گوسی در ریاضیات به صورت کلی مطابق با رابطه زیر تعریف میشود.
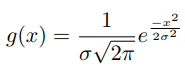
یکی از مهمترین ویژگیهای تابع گاوسی در رابطه زیر بیان شده است. این رابطه نشان میدهد که انتگرال تابع گوسی در بازه منفی بینهایت تا مثبت بینهایت برابر با ۱ است.
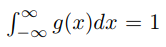
در شکل زیر تبدیل فوریه این تابع مورد بررسی قرار گرفته است. همانطور که مشاهده میشود، تبدیل فوریه یک تابع گاوسی یک تابع گاوسی دیگر را نتیجه میدهد.
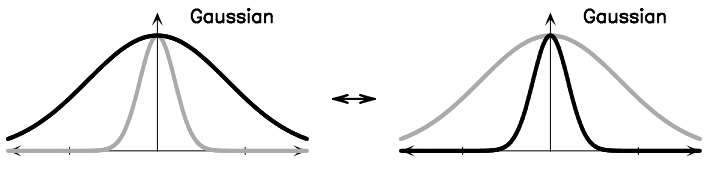
تبدیل فوریه تابع گوسی که رابطه آن بیان شد، به صورت زیر قابل محاسبه است.
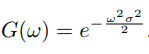
در این رابطه (G(ω، تبدیل فوریه تابع (g(x را نشان میدهد.
تبدیل فوریه دیراک کام
در این قسمت به بررسی تبدیل فوریه یک تابع «دیراک کام» (Dirac Comb) پرداخته میشود. این تابع به تابع شاه (Shah Function) نیز معروف است و کاربرد بسیار زیادی در ریاضیات و مهندسی برق دارد. تابع دیراک کام را میتوان به شکل کلی زیر تعریف کرد.
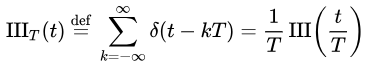
T در این رابطه، دوره تناوب را نشان میدهد. تبدیل فوریه تابع دیراک کام به شکل زیر بیان میشود.
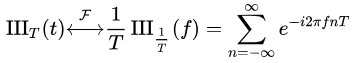
در حالتی که دوره تناوب برابر با یک باشد، تبدیل فوریه تابع دیراک کام با خود آن برابر است. بنابراین داریم:
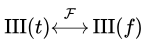
نمودار این تابع و تبدیل فوریه آن در شکل زیر به تصویر کشیده شده است. همانطور که مشاهده میشود این تابع و تبدیل فوریه آن با یکدیگر برابر هستند.

تبدیل فوریه تابع پله
در ادامه به بررسی تبدیل فوریه «تابع پله» (Step Function) پرداخته میشود. تابع پله در ریاضیات یکی از مهمترین توابع برای سادهسازی معادلات مختلف است. این تابع به صورت عمومی به شکل زیر نمایش داده میشود.
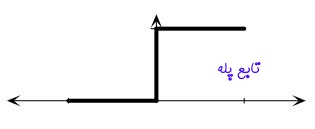
همانطور که مشاهده میشود، تابع پله، تابعی است که مقدار آن در یک عدد مشخصی (در اینجا این عدد مشخص مبدا مختصات است) دچار ناپیوستگی میشود. مقدار تابع قبل از این مقدار مشخص، برابر با صفر و بعد از آن برابر با یک است.
شکل زیر رابطه و شیوه نمایش تبدیل فوریه تابع پلهای که در بالا نشان داده شده را نمایش میدهد.
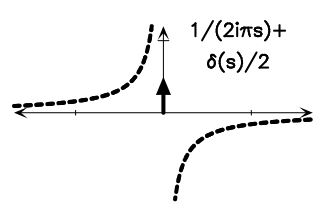
همانطور که مشاهده میشود، تبدیل فوریه تابع پله در مبدا مختصات تعریف نشده و مقدار آن با افزایش فاصله از محورهای مختصات به سمت صفر میکند.
انواع مختلف تبدیلات فوریه در این مطلب مورد بررسی قرار گرفتند. استفاده از این روابط، کمک بسیار زیادی به محاسبه تبدیل فوریه توابع مختلف و استفاده از آن در مسائل گوناگون میکند. در ادامه به بررسی خواص حاکم بر تبدیلات فوریه پرداخته میشود. این خواص، کاربرد بسیار زیادی در مسائل مهندسی و محاسبه سادهتر تبدیل فوریه توابع گوناگون دارد.
خواص پایه تبدیل فوریه
این قسمت به بررسی خواص حاکم بر تبدیلات فوریه میپردازد. این خواص، کاربرد بسیار زیادی برای محاسبه تبدیل فوریه یک تابع پیچیده دارد. برای مثال میتوان یک تابع پیچیده را به مجموع و حاصل ضرب و یا مشتق یک تابع سادهتر تبدیل کرد و در ادامه به کمک روابط داده شده، تبدیل فوریه آن را محاسبه کرد.
خاصیت جمعپذیری
تبدیل فوریه دو تابع (f(x و (g(x را به ترتیب به فرم (F(s و (G(s در نظر بگیرید. در این حالت، تبدیل فوریه مجموع این دو تابع برابر با مجموع تبدیل فوریه هرکدام از این دو تابع است. این موضوع به صورت رابطه زیر نشان داده شده است.
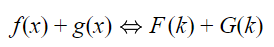
این نتیجه، نشان میدهد که تبدیلات فوریه، خاصیت خطی دارند. در واقع یکی از خواص جالب در این حالت این است که وقتی a یک ثابت در نظر گرفته شود میتوان رابطه زیر را برای حاصل ضرب a در تابع مربوطه بیان کرد.
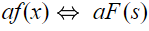
به صورت کلی میتوان این خاصیت را به شکل زیر نمایش داد. این خاصیت به خاصیت «جمعپذیری» (Addition) معروف است.
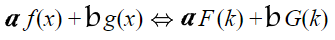
خاصیت شیفت
تبدیل فوریه تابع (f(x را به فرم (F(s در نظر بگیرید. فرض کنید تابع (f(x در طول محور x به اندازه a حرکت و یا به اصطلاح «شیفت» (Shift) کند، در این صورت این تابع با نماد (f(x-a نمایش داده میشود. در این حالت،تبدیل فوریه تابع (f(x-a را میتوان به شکل زیر بیان کرد.
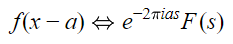
این رابطه، کاربرد بسیار زیادی در محاسبه تبدیل فوریه برخی از توابع پیچیده دارد. در صورتی که این تابع به سمت منفی محور مختصات حرکت کند، علامت منفی در رابطه بالا به فرم مثبت در میآید و خاصیت شیفت به شکل زیر برای تبدیل فوریه این تابع محاسبه خواهد شد.
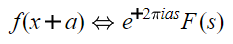

خاصیت تشابه
تبدیل فوریه تابع (f(x را به فرم (F(s در نظر بگیرید. در صورتی که محور x با ضریب ثابت a، مقیاس شود، تابعی به فرم (f(ax خواهیم داشت. در این حالت تبدیل فوریه تابع (f(ax به شکل زیر خواهد بود.
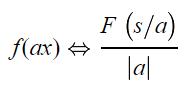
این ویژگی از تبدیلات فوریه، به خاصیت «تشابه» (Similarity) معروف است. طبق رابطه بالا، یک تابع عریض در حوزه زمان به یک تابع نازک در حوزه فرکانس تبدیل خواهد شد. این موضوع به عنوان مطلب پایه در اصل عدم قطعیت مکانیک کوانتوم شناخته میشود.
خاصیت مدولاسیون
در این بخش به بررسی مفهوم «مدولاسیون» (Modulation) دامنه در یک تابع پرداخته میشود. در صورتی که تابع (f(x را در تابع (cos(2πfx ضرب کنیم، تبدیل فوریه تابع حاصل به شکل زیر در میآید.
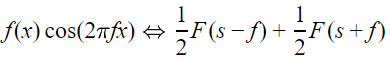
همانطور که مشاهده میشود، تبدیل فوریه ضرب دو تابع مختلف به صورت جمع بیان شده است. این موضوع در علوم مختلف بسیار حائز اهمیت در نظر گرفته میشوند.
خاصیت مشتق
تبدیل فوریه مشتق یک تابع در این قسمت مورد بررسی قرار میگیرد. در صورتی که تابعی با نماد (f(x داشته باشیم، تبدیل فوریه مشتق آن به صورت زیر محاسبه میشود.
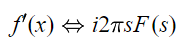
کانولوشن
«کانولوشن» (Convolution)، یکی از مهمترین ویژگیهایی است که در تبدیلات فوریه مشاهده میشود و کاربرد بسیار زیادی در علوم مختلف دارد. این عبارت با نماد * نمایش داده میشود. کانولوشن دو تابع f و g به شکل رابطه زیر قابل نمایش است.
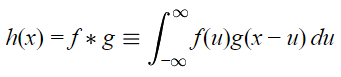
شکل زیر نمونهای از کاربرد کانولوشن را نمایش میدهد. همانطور که نشان داده شده است کانولوشن دو تابع بالا و پایین سمت چپ شکل زیر به فرم تابع نشان داده شده در سمت راست شکل در میآیند.
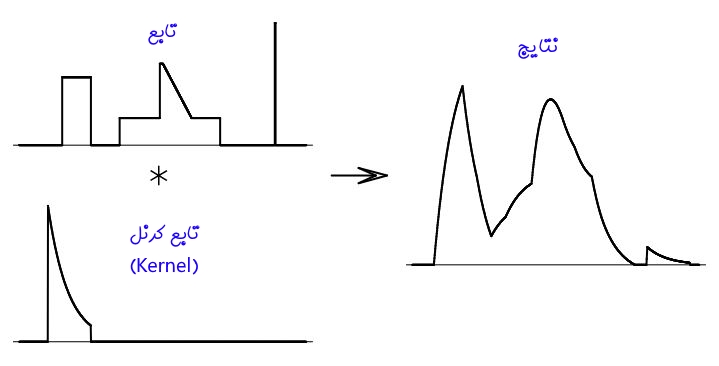
در واقع کانولوش دو تابع را میتوان به فرم انتگرال حاصل ضرب دو تابع در حالیکه یکی از آنها منفی شده و شیفت یافته، بیان کرد. این موضوع با استفاده از رابطه زیر هم قابل محاسبه است. در واقع این رابطه نشان میدهد که به صورت کلی فرقی نمیکند که f و یا g شیفت پیدا کند.
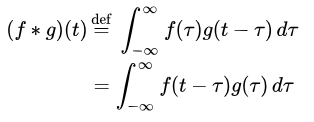
نکته دیگری نیز در تبدیلات فوریه مشاهده میشود که به «تئوری کانولوشن» (Convolution Theorem) مشهور است. این تئوری بیان میکند که تبدیل فوریه کانولوشن دو تابع دلخواه f و g برابر با حاصل ضرب تبدیل فوریه این دو تابع در یکدیگر است. این موضوع در رابطه زیر نشان داده شده است.
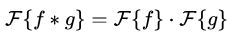
همانطور که اشاره شد، تبدیل فوریه ابزاری ریاضی است که یک شکل موج معلوم را به شکلهای موج دلخواه تبدیل میکند. تبدیل فوریه به ما ابزار قدرتمندی برای بررسی شکل موجهای مختلف ارائه میدهد. در واقع تبدیل فوریه نشان میدهد که هر شکل موج را میتوان به صورت مجموع توابع سینوسی بیان کرد.
این مطلب به صورت دقیق به بررسی مفهوم تبدیل فوریه و روابط حاکم بر آن پرداخته است. در ادامه تبدیل فوریه چند تابع خاص به صورت کامل، مورد مطالعه قرار گرفتند و در نهایت ویژگیهای مختلف تبدیلات فوریه بیان شدند. این ویژگیها کاربرد بسیار زیادی در محاسبه تبدیل فوریه توابع مختلف دارند.












سلام اگه تبدیل فوریه رو روی داده های گسسته برحسب سانتی متر انجام بدیم
نتیجه همون سانتی متر میمونه یا تغییر میکنه؟
سلام اثبات روابط تبدیل فوریه را می خواستم.شما می توانید کمکم کنید؟
برای سیگنال زمان گسسته تابع ضربه چجوری میتونیم ضرایب سری فوریه رو بدست بیاریم؟!
سلام خالد عزیز.
پیشنهاد میکنیم به آموزشهای «تبدیل فوریه گسسته — از صفر تا صد»، «تابع دلتای دیراک — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» و «پاسخ ضربه – به زبان ساده (+ دانلود فیلم آموزش رایگان)» مراجعه کنید.
خوشحالیم که همراه مجله فرادرس هستید.
خیلی خوب بود
خوبه ممنون
خوبه
عالی بود
سلام وقت بخیر
طریقه محاسبه تبدیل فوریه(یک تقسیم بر x)= f(x)
رو لطف میکنید توضیح بدید.
میدونم میشه تابع علامت ولی طریقه حلشو میخوام.
واقعاً از اینکه این مطالب رو با مثالهای بسیار ساده و کاربردی و به صورت رایگان در اختیار ما قرار دادید، سپاسگزارم.
توضیحات عالی.ممنون
سلام وقت بخیر
من دنبال مطالبی راجع به تبدیل فوریه زمان کوتاه هستم . چطور میتونم همه اطلاعات در این مورد رو پیدا کنم ؟
ممنون
تبدیل فوریه سریع تو نرم افزارهای عمرانی چه کاربردی داره؟
سلام.
یکی از کاربردهای تبدیل فوریه سریع، تعیین فرکانسهای غالب یک سیگنال ارتعاشی است که در تحلیل سازه نیز کاربرد دارد. برای آشنایی بیشتر، پیشنهاد میکنیم مطلب «تبدیل فوریه سریع (FFT) — به زبان ساده» را مطالعه کنید.
از اینکه با مجله فرادرس همراه هستید، خوشحالیم.
سلام
این روابطی که در بخش خواص تبدیل فوریه گفتین ، دو طرفه اس یا فقط به همون شکله که در فیلم ها هست ؟
سلام.
روابط برای هر دو برقرارند.
از همراهی شما سپاسگزاریم.
مطلب مفیدی بود. در واقع بسیار مفید. خیلی ممنون
عالی بود و مفید
ممنون از شما
عالی. خیلی استفاده کردم. ممنون