برنامه ریزی خطی در متلب – به زبان ساده (+ دانلود فیلم آموزش رایگان)

برنامه ریزی خطی (Linear Programming) یا LP، یک روش بهینه‌سازی برای سیستمی خطی از قیود یا محدودیت‌ها و یک تابع هدف است که در آن، کمیتی برای بهینه کردن تعریف شده است. هدف از برنامه‌ریزی خطی، یافتن مقادیری از متغیرها است که به ازای آن‌ها تابع هدف کمینه یا بیشینه می‌شود. در این آموزش، در قالب یک مثال ساده، با برنامه‌ریزی خطی آشنا می‌شویم.

مثال ۱

کارخانه‌ای عروسک و فرفره تولید می‌کند. این کارخانه برای تولید هر عروسک ۲ تومان هزینه و ۳ ساعت زمان صرف می‌کند. همچنین، برای تولید هر فرفره ۴ تومان هزینه می‌کند و زمان ساخت آن نیز ۲ ساعت است. کارخانه در یک هفته ۲۲۰ تومان و ۱۵۰ ساعت زمان در اختیار دارد که محصولات خود را تولید کند.

اگر این تولیدی، هر عروسک را ۶ تومان و هر فرفره را ۷ تومان بفروشد، آنگاه باید چه تعداد از هر محصول تولید کند تا در این یک هفته حداکثر سود را داشته باشد؟

برای حل این نوع مسائل، برنامه‌ریزیی خطی گزینه بسیار مناسبی است. زیرا:

• روابط قابل کمیت پذیر در مسئله خطی است.
• مقادیر متغیرها دارای محدودیت یا قید است.
• هدف، یافتن مقادیری از متغیرها است که به ازای آن‌ها یک کمیت بیشینه شود.

برنامه‌ریزی خطی در بسیاری از مسائل که برخاسته از بهینه‌سازی هستند کاربرد دارد. از این روش می‌توان در بهینه‌سازی سود کارخانه‌ها برای تعیین تعداد بهینه نیروی کار و ماشین‌آلات استفاده کرد. از کاربردهای دیگر برنامه‌ریزی خطی می‌توان به تدارکات اشاره کرد که در آن، برای کمینه کردن زمان، تصمیم گرفته می‌شود که چگونه از منابع استفاده گردد.

چه زمانی از برنامه ریزی خطی استفاده می‌کنیم؟

از برنامه‌ریزی خطی می‌توان در مسائلی استفاده کرد که در آن‌ها، هدف بیشینه کردن یک کمیت است و دستگاهی از نامعادلات قیود مسئله را تعریف می‌کنند.

تعریف قید: یک قید یا محدودیت (Constraint)، یک نامساوی است که تعریف می‌کند متغیرهای مسئله چگونه محدودیت دارند. برای استفاده از برنامه‌ریزی خطی، همه قیود باید به صورت نامساوی‌های خطی باشند.

اکنون به مثالی که بیان کردیم باز می‌گردیم.

ادامه مثال ۱

توجه کنید که تولید هر بخش هزینه متناظر با خود را دارد. هزینه هر عروسک ۲ تومان و هزینه هر فرفره ۴ تومان است. همان‌طور که گفتیم، حداکثر هزینه‌ای که کارخانه در یک هفته می‌تواند متقبل شود، ۲۲۰ تومان است. بنابراین، تولید با محدودیت همراه است. متغیر $$x$$ را به عنوان تعداد عروسک‌ها و $$y$$ را به عنوان تعداد فرفره‌های تولیدی در نظر می‌گیریم. بنابراین، قید هزینه شرکت را می‌توان با نامعادله زیر بیان کرد:

$$ \large 2 x + 4 y \le 2 2 0 . $$

 علاوه بر هزینه، برای زمان تولید محصولات نیز محدودیت وجود دارد. هر عروسک در ۳ ساعت و هر فرفره در ۲ ساعت ساخته می‌شوند و کارخانه در هر هفته ۱۵۰ ساعت زمان کاری دارد. قید زمان تولید را نیز می‌توانیم به صورت زیر بیان کنیم:

$$ \large 3 x + 2 y \le 1 5 0 . $$

علاوه بر این قیود، یک درک عام نیز داریم که تعداد قطعات نمی‌تواند کوچک‌تر از صفر باشد و آن را به صورت زیر می‌نویسیم:

$$ \large \begin {aligned} x & \ge 0 \\ y & \ge 0 . \end {aligned} $$

این قیود، قیود نامنفی (Non-negative Constraints) نامیده می‌شوند. در نهایت همه قیود مسئله به صورت زیر هستند:

$$ \large \begin {cases} \begin {aligned} 2 x + 4 y & \le 2 2 0 \\ 3 x + 2 y & \le 1 5 0 \\ x & \ge 0 \\ y & \ge 0 . \end {aligned} \end {cases} $$

نمودار این نامعادلات در صفحه مختصات یک چندضلعی مطابق شکل زیر است.

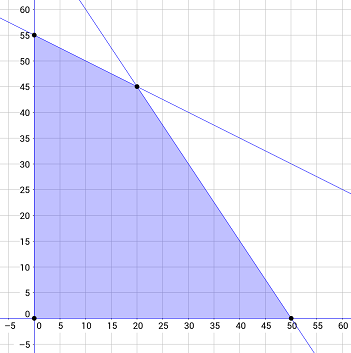
ناحیه سایه زده شده شکل بالا، ناحیه شدنی مسئله نامیده می‌شود.

تعریف ناحیه شدنی: ناحیه‌ای که به قیود سیستم محدود می‌شود، ناحیه شدنی (Feasible Region) نامیده می‌شود. این ناحیه، مقادیر ممکن متغیرهایی را نشان می‌دهد که در همه قیود صدق می‌کنند. برای آنکه برنامه‌ریزی خطی قابل اعمال باشد، ناحیه شدنی باید یک چندبر یا چندسقفی محدب (Convex Polytope) باشد (در حالت دوبعدی، یک چندضلعی محدب و در حالت سه‌بعدی، یک چندوجهی محدب و...).

یافتن ناحیه شدنی تنها برای جواب‌های ممکن مسئله کافی است. هدف برنامه‌ریزی خطی یافتن بهترین جواب برای مسئله است. این کار با کمینه‌سازی یا بیشینه‌سازی تابع هدف انجام می‌شود.

تعریف تابع هدف: تابع هدف (Objective Function) تابعی است که کمیتی را که باید کمینه یا بیشینه شود تعریف می‌کند. متغیرهای تابع هدف همان متغیرهایی هستند که در قیود وجود دارند. برای آنکه بتوانیم از برنامه‌ریزی خطی استفاده کنیم، تابع هدف باید خطی باشد.

ادامه مثال ۱

گفتیم که هزینه ساخت عروسک‌ها ۲ تومان است و هر یک ۶ تومان به فروش می‌رسند. در نتیجه، به ازای تولید هر عروسک ۴ تومان سود وجود خواهد داشت. به همین ترتیب، هزینه تولید و فروش هر فرفره، به ترتیب، ۴ و ۷ تومان است و سودی برابر با ۳ تومان خواهد داشت. تابع سود را به صورت زیر تعریف می‌کنیم:

$$ \large p ( x , y ) = 4 x + 3 y . $$

تابع بالا، همان تابع هدف مسئله است که قصد داریم آن را بیشینه کنیم.

به نظر می‌رسد اکنون باید زوج مرتب‌های ناحیه شدنی را تا یافتن یک سود حداکثر آزمایش کنیم. البته یک روش کارآمدتر برای بیشینه‌سازی تابع وجود دارد.

ادامه مثال ۱

فرض کنید $$P$$ حداکثر سود در ناحیه شدنی باشد:

 $$ \large P = 4 x + 3 y . $$

با حل معادله بالا برای $$y$$، داریم:

$$ \large y = - \frac { 4 } { 3 } x + \frac { P } { 3 } . $$

این حداکثر سود معادله یک خط است. هر نقطه‌ای از ناحیه شدنی که روی این خط قرار داشته باشد، جواب بهینه است. عرض از مبدأ این خط $$ \frac{P}{3} $$ است. از آنجایی که $$P$$ بیشینه شده است، این عرض از مبدأ نیز باید حداکثر باشد.

نمودار چند خط با شیب مشابه $$ - \frac {4}{3}$$ در شکل زیر نشان داده شده است.

خطی که عرض از مبدأ را بیشینه می‌کند، همانی است که از رأس $$(20, 45)$$ چندضلعی، محل تقاطع دو قید عبور می‌کند. خطوط بالاتر از این خط در ناحیه شدنی قرار ندارند. خط‌های پایین‌تر از آن نیز از بیش از دو نقطه از ناحیه شدنی عبور می‌کنند و عرض از مبدأ خط را بیشینه نمی‌کنند.

در نهایت، پس از حل مسئله می‌توان گفت که کارخانه باید ۲۰ عروسک و ۴۵ فرفره تولید کند. با این شرایط، کارخانه ۲۱۵ تومان سود خواهد کرد.

برنامه‌ریزی خطی با دو متغیر

در مثال ادامه‌دار قبلی دیدیم که جواب بهینه یکی از رئوس ناحیه شدنی بود. این مورد در همه مسائل برنامه‌ریزی خطی برقرار است.

قضیه: برای یک ناحیه شدنیِ چندضلعی محدب و یک تابع هدف خطی، جوابی که تابع هدف را کمینه یا بیشینه می‌کند، در یکی از رئوس ناحیه شدنی واقع شده است.

اثبات: تابع هدف $$ f ( x , y ) = a x + b y $$ را در نظر بگیرید. فرض کنید حداکثر مقدار این تابع $$P$$ و حداقل مقدار آن $$Q $$ باشد. بنابراین، خطوطی وجود دارند که هر یک از جواب‌های بهینه $$ (x , y ) $$ می‌گذرند:

$$ \large \begin {aligned} a x + b y & = P & & \qquad ( 1 ) \\ a x + b y & = Q & & \qquad ( 2 ) \\\\ \Rightarrow y & = - \frac { a }{ b } x + \frac { P } { b } & & \qquad ( 1 ) \\ y & = - \frac { a } { b } x + \frac { Q } { b } . & & \qquad ( 2 ) \end {aligned} $$

از آنجایی که $$P$$ مقدار بیشینه تابع هدف است، معادله (۱) دارای عرض از مبدئی برای خطی با شیب $$ - \frac { a } { b } $$ است که از ناحیه شدنی عبور می‌کند. به طور مشابه، معادله (۲)، دارای یک مقدار عرض از مبدأ کمینه برای خطی با شیب $$- \frac { a } { b } $$ است که از ناحیه شدنی می‌گذرد. از برهان خلف استفاده می‌کنیم.

فرض کنید (۱) یا (۲) از نقطه‌ای می‌گذرند که از رئوس ناحیه شدنی نیست.

• حالت اول: نقطه تقاطع روی یکی از اضلاع ناحیه شدنی قرار دارد که با خطوط (۱) و (۲) موازی است. اگر این حالت رخ دهد، آنگاه خط (۱) یا (۲) نیز شامل یک رأس از ناحیه شدنی هستند که با توجه به فرض بالا می‌دانیم چنین چیزی نمی‌تواند رخ دهد.
• حالت دوم: نقطه تقاطع در جایی درون ناحیه شدنی است. در این حالت، خط در بیش از یک نقطه با ناحیه شدنی تقاطع خواهد داشت. در نتیجه، یک نقطه دیگر، بالاتر یا پایین‌تر، در ناحیه شدنی وجود خواهد داشت که با خطی موازی از آن می‌گذرد. اگر (۱) یا (۲) یک عرض از مبدأ برای خطی داشته باشد که از ناحیه شدنی عبور می‌کند، این مورد نیز نمی‌تواند رخ دهد.

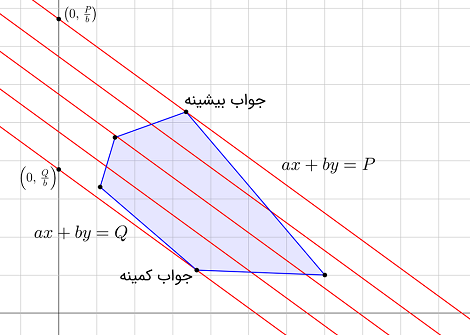
بنابراین، (۱) و (۲) باید یک رأس از ناحیه شدنی را قطع کنند و هر جواب بهینه روی یک رأس ناحیه شدنی واقع شده است.

قضیه‌ای که بیان شد، منجر به روشی ساده برای یافتن جواب بهینه یک مسئله برنامه‌ریزی خطی دومتغیره می‌شود.

فرایند یافتن جواب بهینه یک مسئله برنامه‌ریزی خطی دومتغیره به صورت زیر است:

• مطمئن شوید ناحیه شدنی یک چندضلعی محدب بوده و تابع هدف خطی است.
• زوج مرتب مربوط به هر یک از رئوس ناحیه شدنی را به دست آورید.
• هریک از زوج مرتب‌ها را در تابع هدف جایگذاری کنید تا جوابی که آن را کمینه یا بیشینه می‌کند به دست آید.

مثال ۲

کشاورزی به گاوهایش یک خوراک مکمل ترکیبی می‌دهد تا علاوه بر علوفه اصلی از آن نیز تغذیه کنند. او از دو نوع ماده غذایی برای این ترکیب استفاده می‌کند: یکی ذرت که در هر یک کیلوگرم از آن ۱۰۰ گرم پروتئین و ۷۵۰ گرم نشاسته وجود دارد و دیگری گندم که هر کیلوگرم آن حاوی ۱۵۰ گرم پروتئین و ۷۵۰ گرم نشاسته است. هر گاو باید در طول روز ۷ کیلوگرم مکمل بخورد. کشاورز می‌خواهد هر گاو حداقل ۶۵۰ گرم پروتئین و ۴۰۰۰ گرم نشاسته در روز دریافت کند. اگر هزینه تهیه هر کیلوگرم ذرت و گندم، به ترتیب، ۰٫۴۰ و ۰٫۴۵ تومان باشد، چه ترکیبی از گندم و ذرت هزینه را به حداقل می‌رساند؟

حل: فرض کنید در روز $$c$$ کیلوگرم ذرت و $$w$$ کیلوگرم گندم به هر گاو داده شود. سیستم قیود به صورت زیر خواهد بود:

$$ \large \begin {cases} \begin {aligned} 0 . 1 c + 0 .1 5 w & \ge 0 . 6 5 \\ 0 . 7 5 c + 0 . 7 w & \ge 4 \\ c + w & \le 7 \\ c & \ge 0 \\ w & \ge 0 . \end {aligned} \end {cases} $$

تابع هدف برابر است با:

$$ \large \text {Minimize:} \ f ( c , w ) = 0 . 4 0 c + 0 . 4 5 w . $$

شکل زیر ناحیه شدنی را نشان می‌دهد که در آن، خطوطِ مربوط به قیود یکدیگر را قطع کرده‌اند.

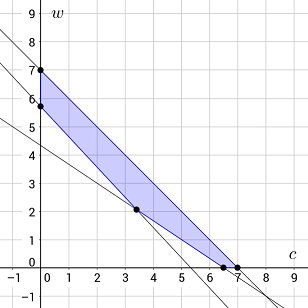
اکنون زوج مرتب متناظر با هر یک از رئوس چندضلعی را از تقاطع خطوط به دست آمده محاسبه می‌کنیم. برای مثال، برای به دست آوردن مختصات رأس ربع اول، دستگاه معادلات زیر را حل می‌کنیم:‌

$$ \large \begin {cases} \begin {aligned} 0 . 1 c + 0 . 1 5 w & = 0 . 6 5 \\ 0 . 7 5 c + 0 . 7 w & = 4 . \end {aligned} \end{cases} $$

با حل دستگاه فوق، مقادیر $$ c \approx 3.411 $$ و $$ w \approx 2.059 $$ به دست می‌آید. این مقادیر را در تابع هدف جایگذاری کرده و هزینه خوراک مکمل را محاسبه می‌کنیم:

$$ \large f ( 3 . 4 1 1, 2 . 0 5 9) = 2 . 2 9 . $$

توجه کنید که لازم نیست مختصات رئوس دیگر را به دست آوریم. از آنجایی که هدف مسئله یافتن یک مقدار کمینه است و شیب تابع هزینه منفی است، جواب بهینه باید روی قسمت زیرین ناحیه شدنی باشد. جواب متناظر با رئوس دیگر به صورت زیر است:

$$ \large \begin {cases} \begin {aligned} 0 . 7 5 c + 0 . 7 w & = 4 \\ c & = 0 \end {aligned} \end {cases} \implies c = 0 , w \approx 5.714 \implies f ( 0 , 5 . 71 4 )= 2.57 $$

$$ \large \begin {cases} \begin {aligned} 0. 1c +0 . 1 5 w & = 0 . 6 5 \\ w & = 0 \end {aligned} \end {cases} \implies c = 6 . 5 , w = 0 \implies f ( 6 . 5 , 0 ) = 2.60 . $$

در نهایت می‌توان گفت که ترکیبی از خوراک مکمل که هزینه را کمینه می‌کند، حاوی ۳۴۱۱ گرم ذرت و ۲۰۵۹ گرم گندم است.

برنامه ریزی خطی در متلب

فرض کنید یک مسئله برنامه‌ریزی خطی با تابع هدف سود زیر داریم:

$$ \large \text{max} \; 143 x + 60 y $$

که در آن، قیود به صورت زیر است:

$$ \large \begin {cases}
\begin {aligned} x + 4 & \le 75 \\
110 x + 30 y & \le 4000 \\
120 x + 210 y & \le 15000 \\
x & \ge 0 \\ y & \ge 0 .
\end {aligned}
\end {cases} $$

برنامه متلب مربوط به نمودار قیود و ناحیه شدنی به صورت زیر است:

>> x = 0:80; % range for graph
>> y1 = max(75 - x,0); % x + y <= 75 farm land
>> y2 = max((4000-110*x)/30,0); % 110x + 30y <= 4000 storage
>> y3 = max((15000 - 120*x)/210,0); % 120x + 210y <= 15000 expenses
>> ytop = min([y1; y2; y3]); % array of minima
>> area(x,ytop); % filled area plot

شکل زیر، نتیجه اجرای برنامه بالا است:‌

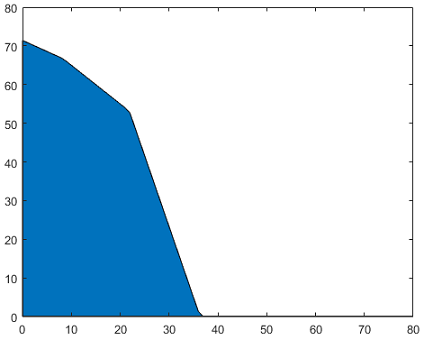
خطوط سود موازی، با برنامه زیر قابل رسم هستند:

>> hold on;
>> [u v] = meshgrid(0:80, 0:80);
>> contour(u,v,143*u + 60*v);
>> hold off;

شکل برنامه بالا به صورت زیر است.

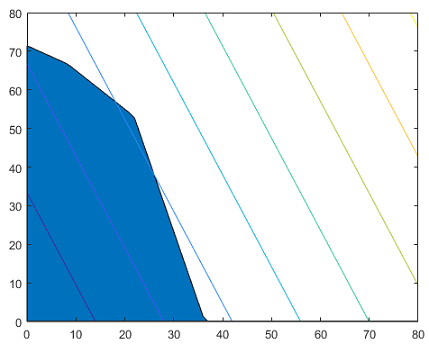
حال که نمایش بصری مسئله را در متلب دیدیم، می‌خواهیم جواب بهینه را به دست آوریم.

دستور linprog

دستور linprog از جعبه‌ابزار بهینه‌سازی متلب، برای حل یک مسئله برنامه‌ریزی خطی به فرم زیر، از الگوریتم سیمپلکس - که در آموزش‌های بعدی آن را توضیح خواهیم داد - استفاده می‌شود:

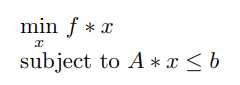
که در آن، $$f$$ یک بردار و $$ A $$ یک ماتریس است و $$b$$ قیود خطی را تعریف می‌کند.

بنابراین، مسئله اصلی را می‌توان به صورت زیر نوشت:‌

به تغییر علامت‌ها برای تبدیل $$\text{max}$$ به $$\text{min}$$ دقت کنید. دوگانی (Duality) در برنامه‌ریزی خطی یک مفهوم بسیار مهم است. برای مثال، در اقتصاد، طبق قاعده دوگانی، کمینه‌سازی هزینه تولید معادل با بیشینه‌سازی سود است.

اکنون می‌توانیم مسئله را در متلب حل کنیم. ابتدا بردارها و ماتریس را به صورت زیر تعریف می‌کنیم:

>> f = [-143 -60]
>> A = [120 210; 110 30; 1 1; -1 0; 0 -1]
>> b = [15000; 4000; 75; 0; 0]

با استفاده از دستور linprog جعبه ابزار بهینه‌سازی متلب، داریم:

>> linprog(f,A,b) % optimize
>> -f*ans % compute profit

پاسخ اجرای این دستورها به صورت زیر است:

Optimal solution found.


ans =

 21.8750
 53.1250

ans =

 6.3156e+03

فیلم آموزش تحقیق در عملیات (برنامه‌ریزی خطی)

برای آشنایی بیشتر با مبحث برنامه‌ریزی خطی می‌توانید به آموزش ویدئویی «تحقیق در عملیات (برنامه‌ریزی خطی)» مراجعه کنید. در این آموزش که مدت آن ۲ ساعت و ۴۶ دقیقه است، علاوه بر مفاهیم برنامه‌ریزی خطی و مدل‌سازی، روش‌های حل مسائل برنامه‌ریزی خطی از قبیل روش ترسیمی، سیمپلکس و M بزرگ به طور کامل توضیح داده شده است. مباحث پیشرفته‌تری مانند جبر ماتریسی و سیمپلکس اصلاح شده، دوگان مسائل برنامه‌ریزی خطی و تحلیل حساسیت و برنامه‌ریزی پارامتریک نیز از دیگر مطالب این آموزش به حساب می‌آیند که با جزئیات مناسبی شرح داده شده‌اند.

• برای دیدن فیلم آموزش تحقیق در عملیات (برنامه ریزی خطی) + اینجا کلیک کنید.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های الگوریتم‌‌های بهینه‌‌سازی هوشمند
• آموزش تحقیق در عملیات (برنامه‌ریزی خطی)
• مجموعه آموزش‌های دروس ریاضیات
• گنجینه آموزش‌های تحقیق در عملیات
• قاعده سیمپسون — به زبان ساده
• روش نیوتن — به زبان ساده
• مشتق‌گیری عددی – به زبان ساده

^^

فیلم‌ های آموزش برنامه ریزی خطی در متلب – به زبان ساده (+ دانلود فیلم آموزش رایگان)

فیلم آموزشی مدلسازی برنامه‌ریزی خطی

فیلم آموزشی حل برنامه‌ریزی خطی

فیلم آموزشی برنامه ریزی خطی در متلب