حل مساله بیشینه جریان — راهنمای جامع

در این مطلب، روش حل مساله بیشینه جریان (Maximum Flow Problem) بیان و راهکار بیان شده برای آن در زبان‌های برنامه‌نویسی گوناگون شامل «سی‌پلاس‌پلاس» (++C)، «جاوا» (Java)، «پایتون» (Python) و «سی‌شارپ» (#C) پیاده‌سازی شده است. یک گراف داده شده که نشانگر یک «شبکه جریان» (Flow Network) است و در آن، هر «یال» (Edge) دارای ظرفیت است. همچنین، دو راس s (مبدا | Source) و t (مقصد | Sink) در گراف داده شده است. هدف پیدا کردن بیشینه جریان ممکنی است که از s به t با در نظر داشتن محدودیت‌های زیر، شکل می‌گیرد.

• جریان روی یک یال از ظرفیت داده شده روی آن یال سر ریز نمی‌کند.
• جریان ورودی برای هر راس، به جز s و t، مساوی با جریان خروجی است.

برای مثال، می‌توان گراف زیر را در نظر گرفت.

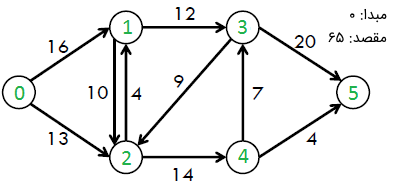
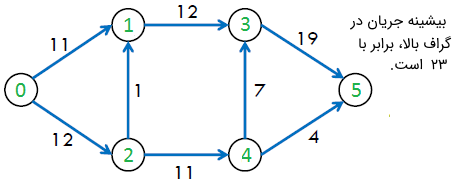
بیشینه جریان ممکن در گراف بالا برابر با ۲۳ است.

الگوریتم فورد–فالکرسون برای حل مساله بیشینه جریان

در ادامه، «الگوریتم فورد–فالکرسون» (Ford-Fulkerson Algorithm) برای حل مساله بیشینه جریان ارائه شده است.

•  با جریان اولیه ۰ شروع کن.
• تا هنگامی که یک مسیر تجمعی از مبدا به مقصد وجود دارد، این «مسیر-جریان» (Path-Flow) را به «جریان» اضافه کن.
• جریان را بازگردان.

پیچیدگی زمانی الگوریتم بالا از درجه O(max_flow * E)‎ است. هنگامی که یک مسیر تجمعی وجود داشته باشد، یک حلقه اجرا می‌شود. در بدترین حالت، ممکن است ۱ واحد جریان در هر تکرار اضافه شود. بنابراین، پیچیدگی زمانی برابر با O(max_flow * E)‎ خواهد شد.

پیاده‌سازی الگوریتم ساده بالا

برای پیاده‌سازی الگوریتم بالا، ابتدا باید مفهوم «گراف باقیمانده» (Residual Graph) تعریف شود که برای درک این پیاده‌سازی مورد نیاز است. گراف باقیمانده از یک شبکه جریان، گرافی است که جریان اضافی ممکن را نشان می‌دهد. اگر مسیری از مبدا به مقصد وجود داشته باشد، این امکان وجود دارد که جریان اضافه شود. هر یال از گراف دارای مقداری است که به آن ظرفیت باقیمانده گفته می‌شود. ظرفیت باقیمانده برابر با ظرفیت اصلی یال‌ها منهای جریان کنونی است. ظرفیت باقیمانده اساسا ظرفیت کنونی یال‌ها است.

اکنون، پیرامون جزئیات پیاده‌سازی صحبت خواهد شد. اگر هیچ یالی بین دو راس از گراف باقیمانده وجود نداشته باشد، ظرفیت باقیمانده برابر با ۰ است. می‌توان با توجه به اینکه هیچ جریان اولیه‌ای وجود ندارد، به گراف باقیمانده مقداردهی اولیه کرد. همچنین، ظرفیت باقیمانده اولیه برابر با ظرفیت اصلی است. برای پیدا کردن مسیر تجمعی، می‌توان از الگوریتم «جستجوی اول سطح» (Breadth-First Search) یا «جستجوی اول عمق» (Depth-First Search) استفاده کرد. در پیاده‌سازی زیر، برای پیدا کردن مسیر تجمعی از BFS استفاده شده است.

با استفاده از BFS، می‌توان بررسی کرد که آیا مسیری از مبدا به مقصد وجود دارد یا خیر. همچنین، BFS، آرایه parent[]‎ را می‌سازد. با استفاده از آرایه parent[]‎، پیمایش در مسیر یافته شده انجام و جریان احتمالی از طریق این مسیر با پیدا کردن ظرفیت باقیمانده در طول مسیر پیدا می‌شود. در ادامه، جریان مسیر یافت شده به جریان کلی اضافه می‌شود. نکته مهم آن است که به روز رسانی ظرفیت باقیمانده‌ها در گراف باقیمانده مورد نیاز است. جریان مسیر از همه یال‌ها در طول مسیر کسر می‌شود و جریان مسیر در امتداد یال‌های معکوس اضافه می‌شود. نیاز به اضافه کردن جریان مسیر در طول یال‌های معکوس است، زیرا ممکن است بعدا نیاز به ارسال جریان در جهت معکوس باشد.

حل مساله بیشینه جریان در ++C

// C++ program for implementation of Ford Fulkerson algorithm 
#include <iostream> 
#include <limits.h> 
#include <string.h> 
#include <queue> 
using namespace std; 
  
// Number of vertices in given graph 
#define V 6 
  
/* Returns true if there is a path from source 's' to sink 't' in 
  residual graph. Also fills parent[] to store the path */
bool bfs(int rGraph[V][V], int s, int t, int parent[]) 
{ 
    // Create a visited array and mark all vertices as not visited 
    bool visited[V]; 
    memset(visited, 0, sizeof(visited)); 
  
    // Create a queue, enqueue source vertex and mark source vertex 
    // as visited 
    queue <int> q; 
    q.push(s); 
    visited[s] = true; 
    parent[s] = -1; 
  
    // Standard BFS Loop 
    while (!q.empty()) 
    { 
        int u = q.front(); 
        q.pop(); 
  
        for (int v=0; v<V; v++) 
        { 
            if (visited[v]==false && rGraph[u][v] > 0) 
            { 
                q.push(v); 
                parent[v] = u; 
                visited[v] = true; 
            } 
        } 
    } 
  
    // If we reached sink in BFS starting from source, then return 
    // true, else false 
    return (visited[t] == true); 
} 
  
// Returns the maximum flow from s to t in the given graph 
int fordFulkerson(int graph[V][V], int s, int t) 
{ 
    int u, v; 
  
    // Create a residual graph and fill the residual graph with 
    // given capacities in the original graph as residual capacities 
    // in residual graph 
    int rGraph[V][V]; // Residual graph where rGraph[i][j] indicates  
                     // residual capacity of edge from i to j (if there 
                     // is an edge. If rGraph[i][j] is 0, then there is not)   
    for (u = 0; u < V; u++) 
        for (v = 0; v < V; v++) 
             rGraph[u][v] = graph[u][v]; 
  
    int parent[V];  // This array is filled by BFS and to store path 
  
    int max_flow = 0;  // There is no flow initially 
  
    // Augment the flow while tere is path from source to sink 
    while (bfs(rGraph, s, t, parent)) 
    { 
        // Find minimum residual capacity of the edges along the 
        // path filled by BFS. Or we can say find the maximum flow 
        // through the path found. 
        int path_flow = INT_MAX; 
        for (v=t; v!=s; v=parent[v]) 
        { 
            u = parent[v]; 
            path_flow = min(path_flow, rGraph[u][v]); 
        } 
  
        // update residual capacities of the edges and reverse edges 
        // along the path 
        for (v=t; v != s; v=parent[v]) 
        { 
            u = parent[v]; 
            rGraph[u][v] -= path_flow; 
            rGraph[v][u] += path_flow; 
        } 
  
        // Add path flow to overall flow 
        max_flow += path_flow; 
    } 
  
    // Return the overall flow 
    return max_flow; 
} 
  
// Driver program to test above functions 
int main() 
{ 
    // Let us create a graph shown in the above example 
    int graph[V][V] = { {0, 16, 13, 0, 0, 0}, 
                        {0, 0, 10, 12, 0, 0}, 
                        {0, 4, 0, 0, 14, 0}, 
                        {0, 0, 9, 0, 0, 20}, 
                        {0, 0, 0, 7, 0, 4}, 
                        {0, 0, 0, 0, 0, 0} 
                      }; 
  
    cout << "The maximum possible flow is " << fordFulkerson(graph, 0, 5); 
  
    return 0; 
}

حل مساله بیشینه جریان در جاوا

// Java program for implementation of Ford Fulkerson algorithm 
import java.util.*; 
import java.lang.*; 
import java.io.*; 
import java.util.LinkedList; 
  
class MaxFlow 
{ 
    static final int V = 6;    //Number of vertices in graph 
  
    /* Returns true if there is a path from source 's' to sink 
      't' in residual graph. Also fills parent[] to store the 
      path */
    boolean bfs(int rGraph[][], int s, int t, int parent[]) 
    { 
        // Create a visited array and mark all vertices as not 
        // visited 
        boolean visited[] = new boolean[V]; 
        for(int i=0; i<V; ++i) 
            visited[i]=false; 
  
        // Create a queue, enqueue source vertex and mark 
        // source vertex as visited 
        LinkedList<Integer> queue = new LinkedList<Integer>(); 
        queue.add(s); 
        visited[s] = true; 
        parent[s]=-1; 
  
        // Standard BFS Loop 
        while (queue.size()!=0) 
        { 
            int u = queue.poll(); 
  
            for (int v=0; v<V; v++) 
            { 
                if (visited[v]==false && rGraph[u][v] > 0) 
                { 
                    queue.add(v); 
                    parent[v] = u; 
                    visited[v] = true; 
                } 
            } 
        } 
  
        // If we reached sink in BFS starting from source, then 
        // return true, else false 
        return (visited[t] == true); 
    } 
  
    // Returns tne maximum flow from s to t in the given graph 
    int fordFulkerson(int graph[][], int s, int t) 
    { 
        int u, v; 
  
        // Create a residual graph and fill the residual graph 
        // with given capacities in the original graph as 
        // residual capacities in residual graph 
  
        // Residual graph where rGraph[i][j] indicates 
        // residual capacity of edge from i to j (if there 
        // is an edge. If rGraph[i][j] is 0, then there is 
        // not) 
        int rGraph[][] = new int[V][V]; 
  
        for (u = 0; u < V; u++) 
            for (v = 0; v < V; v++) 
                rGraph[u][v] = graph[u][v]; 
  
        // This array is filled by BFS and to store path 
        int parent[] = new int[V]; 
  
        int max_flow = 0;  // There is no flow initially 
  
        // Augment the flow while tere is path from source 
        // to sink 
        while (bfs(rGraph, s, t, parent)) 
        { 
            // Find minimum residual capacity of the edhes 
            // along the path filled by BFS. Or we can say 
            // find the maximum flow through the path found. 
            int path_flow = Integer.MAX_VALUE; 
            for (v=t; v!=s; v=parent[v]) 
            { 
                u = parent[v]; 
                path_flow = Math.min(path_flow, rGraph[u][v]); 
            } 
  
            // update residual capacities of the edges and 
            // reverse edges along the path 
            for (v=t; v != s; v=parent[v]) 
            { 
                u = parent[v]; 
                rGraph[u][v] -= path_flow; 
                rGraph[v][u] += path_flow; 
            } 
  
            // Add path flow to overall flow 
            max_flow += path_flow; 
        } 
  
        // Return the overall flow 
        return max_flow; 
    } 
  
    // Driver program to test above functions 
    public static void main (String[] args) throws java.lang.Exception 
    { 
        // Let us create a graph shown in the above example 
        int graph[][] =new int[][] { {0, 16, 13, 0, 0, 0}, 
                                     {0, 0, 10, 12, 0, 0}, 
                                     {0, 4, 0, 0, 14, 0}, 
                                     {0, 0, 9, 0, 0, 20}, 
                                     {0, 0, 0, 7, 0, 4}, 
                                     {0, 0, 0, 0, 0, 0} 
                                   }; 
        MaxFlow m = new MaxFlow(); 
  
        System.out.println("The maximum possible flow is " + 
                           m.fordFulkerson(graph, 0, 5)); 
  
    } 
} 

حل مساله بیشینه جریان در پایتون

# Python program for implementation of Ford Fulkerson algorithm 
   
from collections import defaultdict 
   
#This class represents a directed graph using adjacency matrix representation 
class Graph: 
   
    def __init__(self,graph): 
        self.graph = graph # residual graph 
        self. ROW = len(graph) 
        #self.COL = len(gr[0]) 
          
   
    '''Returns true if there is a path from source 's' to sink 't' in 
    residual graph. Also fills parent[] to store the path '''
    def BFS(self,s, t, parent): 
  
        # Mark all the vertices as not visited 
        visited =[False]*(self.ROW) 
          
        # Create a queue for BFS 
        queue=[] 
          
        # Mark the source node as visited and enqueue it 
        queue.append(s) 
        visited[s] = True
           
         # Standard BFS Loop 
        while queue: 
  
            #Dequeue a vertex from queue and print it 
            u = queue.pop(0) 
          
            # Get all adjacent vertices of the dequeued vertex u 
            # If a adjacent has not been visited, then mark it 
            # visited and enqueue it 
            for ind, val in enumerate(self.graph[u]): 
                if visited[ind] == False and val > 0 : 
                    queue.append(ind) 
                    visited[ind] = True
                    parent[ind] = u 
  
        # If we reached sink in BFS starting from source, then return 
        # true, else false 
        return True if visited[t] else False
              
      
    # Returns tne maximum flow from s to t in the given graph 
    def FordFulkerson(self, source, sink): 
  
        # This array is filled by BFS and to store path 
        parent = [-1]*(self.ROW) 
  
        max_flow = 0 # There is no flow initially 
  
        # Augment the flow while there is path from source to sink 
        while self.BFS(source, sink, parent) : 
  
            # Find minimum residual capacity of the edges along the 
            # path filled by BFS. Or we can say find the maximum flow 
            # through the path found. 
            path_flow = float("Inf") 
            s = sink 
            while(s !=  source): 
                path_flow = min (path_flow, self.graph[parent[s]][s]) 
                s = parent[s] 
  
            # Add path flow to overall flow 
            max_flow +=  path_flow 
  
            # update residual capacities of the edges and reverse edges 
            # along the path 
            v = sink 
            while(v !=  source): 
                u = parent[v] 
                self.graph[u][v] -= path_flow 
                self.graph[v][u] += path_flow 
                v = parent[v] 
  
        return max_flow 
  
   
# Create a graph given in the above diagram 
  
graph = [[0, 16, 13, 0, 0, 0], 
        [0, 0, 10, 12, 0, 0], 
        [0, 4, 0, 0, 14, 0], 
        [0, 0, 9, 0, 0, 20], 
        [0, 0, 0, 7, 0, 4], 
        [0, 0, 0, 0, 0, 0]] 
  
g = Graph(graph) 
  
source = 0; sink = 5
   
print ("The maximum possible flow is %d " % g.FordFulkerson(source, sink)) 
  
#This code is contributed by Neelam Yadav 

حل مساله بیشینه جریان در #C

// C# program for implementation  
// of Ford Fulkerson algorithm 
using System; 
using System.Collections.Generic; 
  
public class MaxFlow 
{ 
    static readonly int V = 6; //Number of vertices in graph 
  
    /* Returns true if there is a path 
    from source 's' to sink 't' in residual 
    graph. Also fills parent[] to store the 
    path */
    bool bfs(int [,]rGraph, int s, int t, int []parent) 
    { 
        // Create a visited array and mark  
        // all vertices as not visited 
        bool []visited = new bool[V]; 
        for(int i = 0; i < V; ++i) 
            visited[i] = false; 
  
        // Create a queue, enqueue source vertex and mark 
        // source vertex as visited 
        List<int> queue = new List<int>(); 
        queue.Add(s); 
        visited[s] = true; 
        parent[s] = -1; 
  
        // Standard BFS Loop 
        while (queue.Count != 0) 
        { 
            int u = queue[0]; 
                queue.RemoveAt(0); 
  
            for (int v = 0; v < V; v++) 
            { 
                if (visited[v] == false && rGraph[u, v] > 0) 
                { 
                    queue.Add(v); 
                    parent[v] = u; 
                    visited[v] = true; 
                } 
            } 
        } 
  
        // If we reached sink in BFS  
        // starting from source, then 
        // return true, else false 
        return (visited[t] == true); 
    } 
  
    // Returns tne maximum flow 
    // from s to t in the given graph 
    int fordFulkerson(int [,]graph, int s, int t) 
    { 
        int u, v; 
  
        // Create a residual graph and fill  
        // the residual graph with given  
        // capacities in the original graph as 
        // residual capacities in residual graph 
  
        // Residual graph where rGraph[i,j]  
        // indicates residual capacity of  
        // edge from i to j (if there is an  
        // edge. If rGraph[i,j] is 0, then  
        // there is not) 
        int [,]rGraph = new int[V, V]; 
  
        for (u = 0; u < V; u++) 
            for (v = 0; v < V; v++) 
                rGraph[u, v] = graph[u, v]; 
  
        // This array is filled by BFS and to store path 
        int []parent = new int[V]; 
  
        int max_flow = 0; // There is no flow initially 
  
        // Augment the flow while tere is path from source 
        // to sink 
        while (bfs(rGraph, s, t, parent)) 
        { 
            // Find minimum residual capacity of the edhes 
            // along the path filled by BFS. Or we can say 
            // find the maximum flow through the path found. 
            int path_flow = int.MaxValue; 
            for (v = t; v != s; v = parent[v]) 
            { 
                u = parent[v]; 
                path_flow = Math.Min(path_flow, rGraph[u,v]); 
            } 
  
            // update residual capacities of the edges and 
            // reverse edges along the path 
            for (v = t; v != s; v = parent[v]) 
            { 
                u = parent[v]; 
                rGraph[u,v] -= path_flow; 
                rGraph[v,u] += path_flow; 
            } 
  
            // Add path flow to overall flow 
            max_flow += path_flow; 
        } 
  
        // Return the overall flow 
        return max_flow; 
    } 
  
    // Driver code 
    public static void Main () 
    { 
        // Let us create a graph shown in the above example 
        int [,]graph =new int[,] { {0, 16, 13, 0, 0, 0}, 
                                    {0, 0, 10, 12, 0, 0}, 
                                    {0, 4, 0, 0, 14, 0}, 
                                    {0, 0, 9, 0, 0, 20}, 
                                    {0, 0, 0, 7, 0, 4}, 
                                    {0, 0, 0, 0, 0, 0} 
                                }; 
        MaxFlow m = new MaxFlow(); 
  
        Console.WriteLine("The maximum possible flow is " + 
                        m.fordFulkerson(graph, 0, 5)); 
  
    } 
} 
  
/* This code contributed by PrinciRaj1992 */

خروجی قطعه کدهای بالا به صورت زیر است.

The maximum possible flow is 23

پیاده‌سازی بالا از الگوریتم فورد–فالکرسون را «الگوریتم ادموندز کارپ» (Edmonds-Karp Algorithm) می‌گویند. ایده اصلی نهفته در پس استفاده از الگوریتم ادموندز کارپ، استفاده از BFS است؛ زیرا BFS همیشه مسیری با کمترین تعداد یال را انتخاب می‌کند.

هنگامی که BFS مورد استفاده قرار می‌گیرد، پیچیدگی زمانی بدترین حالت را می‌توان به O(VE²)‎ کاهش داد. پیاده‌سازی بالا از ارائه ماتریس مجاورت استفاده می‌کند و BFS دارای پیچیدگی زمانی از درجه O(V²)‎ است.

این مسأله با توجه به اینکه در بسیاری از موقعیت‌های عملی به وقوع می‌پیوندد، بسیار حائز است. از جمله مثال‌هایی برای مسأله بیشینه جریان می‌توان زد، افزایش حمل و نقل با توجه به محدودیت‌های ترافیکی داده شده و افزایش جریان بسته‌ها در شبکه‌های کامپیوتری است.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• الگوریتم بازی مار و پله همراه با کد — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده

^^