۵ الگوریتم مرتب سازی در پایتون — راهنمای کاربردی

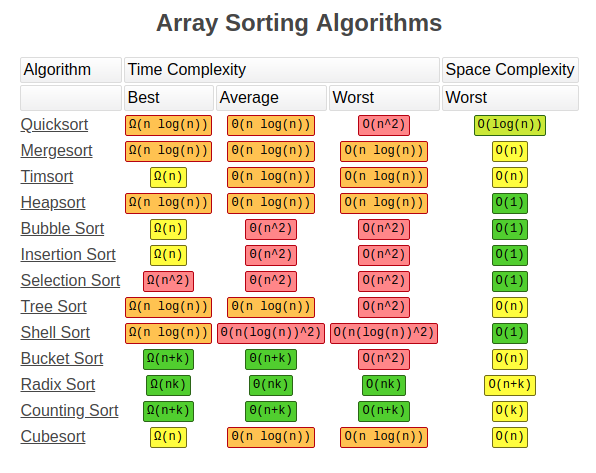
مرتب سازی یکی از مهارت‌هایی است که هر مهندس نرم‌افزار و توسعه‌دهنده‌ای باید از آن مطلع باشد. این مهارت نه تنها جهت موفقیت در مصاحبه‌های شغلی بلکه به عنوان یک دانش عمومی برنامه‌نویسی همواره مورد نیاز است. الگوریتم‌های مرتب‌سازی مختلف به خوبی نشان می‌دهند که چگونه یک طراحی مناسب می‌تواند چنان تأثیر شگرفی روی پیچیدگی، سرعت و کارایی برنامه داشته باشند. در این نوشته به مقایسه 5 الگوریتم مرتب‌ سازی در پایتون می‌پردازیم که کارایی بیشتری دارند و سپس نحوه پیاده‌سازی آن‌ها را نیز مرور خواهیم کرد.

مرتب‌سازی حبابی (Bubble Sort)

مرتب‌سازی حبابی یکی از الگوریتم‌هایی است که معمولاً در دوره‌های مقدماتی کلاس‌های علوم رایانه ارائه می‌شود، چون به روشنی طرز کار مرتب‌سازی را نشان می‌دهد و همزمان درک آن نیز ساده و آسان است.

فیلم آموزش الگوریتم های مرتب سازی در زبان برنامه نویسی پایتون با مثال (رایگان) در فرادرس

کلیک کنید

مراحل مرتب‌سازی حبابی از طریق یک لیست و مقایسه عناصر مجاور صورت می‌گیرد. در این فرایند وقتی عناصر در ترتیب نادرستی باشند، با هم دیگر تعویض می‌شوند. این عملیات روی آرایه‌ها تا زمانی که هیچ دو عنصر مجاوری در ترتیب نادرست نباشند، ادامه می‌یابد. از آنجا که مرتب‌سازی حبابی به طور مکرر روی بخش مرتب نشده لیست انجام می‌یابد، مقدار پیچیدگی آن در بدترین حالت برابر با $$O(n^2)$$ است.

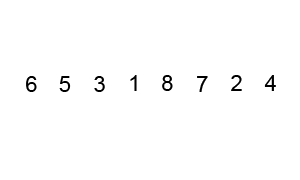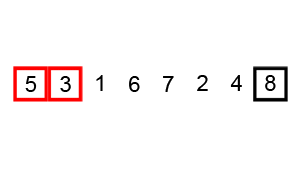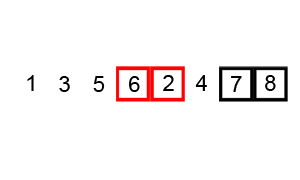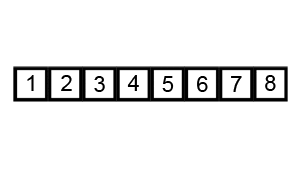
def bubble_sort(arr):
    def swap(i, j):
        arr[i], arr[j] = arr[j], arr[i]

    n = len(arr)
    swapped = True
    
    x = -1
    while swapped:
        swapped = False
        x = x + 1
        for i in range(1, n-x):
            if arr[i - 1] > arr[i]:
                swap(i - 1, i)
                swapped = True
                    
return arr

مرتب‌سازی انتخابی (Selection Sort)

مرتب‌سازی انتخابی کاملاً ساده است؛ اما با این حال در اغلب موارد عملکردی بهتر از مرتب‌سازی حبابی دارد. اگر قرار است یکی از این دو روش را انتخاب کنید، در اغلب موارد بدون بررسی می‌توان گفت که مرتب‌سازی انتخابی، گزینه بهتری است. ما در مرتب‌سازی انتخابی، لیست یا آرایه ورودی خود را به دو بخش تقسیم می‌کنیم. یک بخش زیرمجموعه مرتب شده است و بخش دیگر زیرمجموعه‌ای است که همچنان منتظر مرتب‌سازی است. ابتدا کوچک‌ترین عنصر را در زیرمجموعه نامرتب انتخاب کرده و آن را در انتهای زیرمجموعه مرتب قرار می‌دهیم. از این رو به طور مرتب کوچک‌ترین عنصر نامرتب را بر می‌داریم و آن را در انتهای زیرمجموعه مرتب قرار می‌دهیم. این فرایند تا زمانی که کل عناصر به لیست مرتب انتقال یابند ادامه می‌یابد.

def selection_sort(arr):        
    for i in range(len(arr)):
        minimum = i
        
        for j in range(i + 1, len(arr)):
            # Select the smallest value
            if arr[j] < arr[minimum]:
                minimum = j

        # Place it at the front of the 
        # sorted end of the array
        arr[minimum], arr[i] = arr[i], arr[minimum]
            
return arr

مرتب‌سازی درجی (Insertion Sort)

مرتب‌سازی درجی از هر دو روش مرتب‌سازی حبابی و انتخابی که در بخش فوق اشاره کردیم هم سریع‌تر و هم ساده‌تر است. این روش تا حدود زیادی شبیه روش مرتب‌سازی کارت‌های بازی است که اغلب افراد به طور غریزی انجام می‌دهند. در این روش در هر تکرار یک عنصر از آرایه برداشته می‌شود. سپس موقعیت آن عنصر در آرایه در صورتی که مرتب باشد پیدا می‌شود. این فرایند تا زمانی که همه عناصر ورودی جایگاه خود را در آرایه مرتب بیابند تداوم می‌یابد.

def insertion_sort(arr, simulation=False):
        
    for i in range(len(arr)):
        cursor = arr[i]
        pos = i
        
        while pos > 0 and arr[pos - 1] > cursor:
            # Swap the number down the list
            arr[pos] = arr[pos - 1]
            pos = pos - 1
        # Break and do the final swap
        arr[pos] = cursor

return arr

مرتب‌سازی ادغامی (Merge Sort)

مرتب‌سازی ادغامی یک نمونه کاملاً عالی از الگوریتم تقسیم و حل (Divide and Conquer) محسوب می‌شود. در این روش مرتب سازی صرفاً از 2 مرحله آن الگوریتم استفاده می‌شود که شامل تقسیم پیوسته و ادغام مکرر است.

تقسیم پیوسته

در این مرحله لیست نامرتب به طور پیوسته تقسیم می‌شود تا این که به N زیرمجموعه برسیم. در این حالت هر زیرمجموعه 1 عنصر دارد که نامرتب است و N تعداد عناصر لیست اصلی است.

ادغام مکرر

این همان مرحله حل در الگوریتم تقسیم و حل است و در آن زیرمجموعه‌ها دو به دو با هم ادغام می‌شوند تا زیرمجموعه‌های جدید مرتبی را شکل بدهند. این کار تا زمانی که همه زیرمجموعه‌ها با هم ادغام شوند و یک آرایه کامل مرتب تشکیل دهند ادامه می‌یابد.

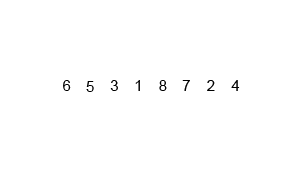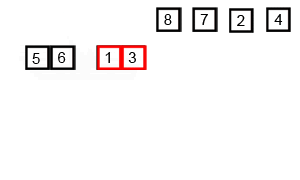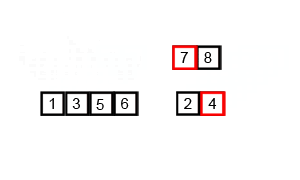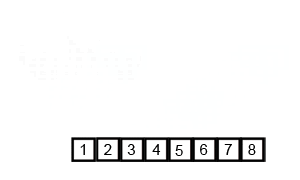
def merge_sort(arr):
    # The last array split
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    # Perform merge_sort recursively on both halves
    left, right = merge_sort(arr[:mid]), merge_sort(arr[mid:])

    # Merge each side together
    return merge(left, right, arr.copy())


def merge(left, right, merged):

    left_cursor, right_cursor = 0, 0
    while left_cursor < len(left) and right_cursor < len(right):
      
        # Sort each one and place into the result
        if left[left_cursor] <= right[right_cursor]:
            merged[left_cursor+right_cursor]=left[left_cursor]
            left_cursor += 1
        else:
            merged[left_cursor + right_cursor] = right[right_cursor]
            right_cursor += 1
            
    for left_cursor in range(left_cursor, len(left)):
        merged[left_cursor + right_cursor] = left[left_cursor]
        
    for right_cursor in range(right_cursor, len(right)):
        merged[left_cursor + right_cursor] = right[right_cursor]

return merged

مرتب‌سازی سریع (Quick Sort)

مرتب‌سازی سریع نیز یک الگوریتم «تقسیم و حل» مانند مرتب‌سازی ادغامی است. با این که این روش کمی پیچیده‌تر است؛ اما در اغلب موارد، پیاده‌سازی استاندارد آن به طور قابل توجهی سریع‌تر از مرتب‌سازی ادغامی عمل می‌کند و به ندرت به پیچیدگی بدترین حالت خود یعنی $$O(n^2)$$ می‌رسد. این روش مرتب‌سازی 3 مرحله به صورت زیر دارد.

1. در ابتدا یک عنصر از آرایه انتخاب می‌کنیم که آن را محور (pivot) آرایه می‌نامیم.
2. همه عناصر کوچک‌تر از محور را به سمت چپ آن انتقال می‌دهیم. سپس همه عناصر بزرگ‌تر از محور را به سمت راست آن انتقال می‌دهیم. این کار عملیات افراز نامیده می‌شود.
3. دو مرحله فوق را به صورت بازگشتی و جداگانه روی هر یک از زیرمجموعه‌های عناصر به صورت مقادیر بزرگ‌تر و کوچک‌تر از آخرین محور اجرا می‌کنیم.

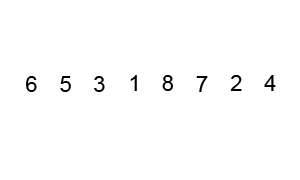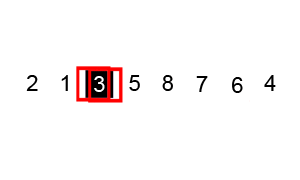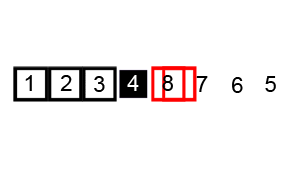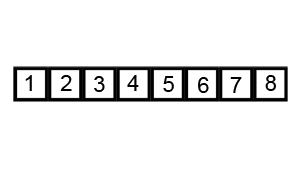
def partition(array, begin, end):
    pivot_idx = begin
    for i in xrange(begin+1, end+1):
        if array[i] <= array[begin]:
            pivot_idx += 1
            array[i], array[pivot_idx] = array[pivot_idx], array[i]
    array[pivot_idx], array[begin] = array[begin], array[pivot_idx]
    return pivot_idx

def quick_sort_recursion(array, begin, end):
    if begin >= end:
        return
    pivot_idx = partition(array, begin, end)
    quick_sort_recursion(array, begin, pivot_idx-1)
    quick_sort_recursion(array, pivot_idx+1, end)

def quick_sort(array, begin=0, end=None):
    if end is None:
        end = len(array) - 1
    
return quick_sort_recursion(array, begin, end)

اگر این مطلب برای شما مفید بوده است و علاقه‌مند به یادگیری بیشتر در این زمینه هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های برنامه نویسی پایتون
• آموزش ساختمان داده ها
• مجموعه آموزش‌های مهندسی نرم افزار
• معرفی تکنیک های مرتب سازی (Sorting Techniques) — ساختار داده و الگوریتم ها
• آموزش روش تقسیم و حل در طراحی الگوریتم
• مرتب سازی نتایج (Sorting Results) در MySQL — راهنمای جامع
• آموزش آرایه ها در زبان برنامه نویسی C

==