یافتن مسیرهای بهینه در برنامه نویسی دینامیک (پویا) – به زبان ساده

در علوم رایانه و ریاضیات، برنامه نویسی دینامیک روشی کارآمد برای حل مسائل جستجو و بهینه‌سازی با استفاده از دو خصیصه «زیر مسئله‌های هم‌پوشان» و «زیرساخت‌های بهینه» است. برخلاف برنامه‌ریزی خطی، چارچوب استانداردی برای فرموله کردن مسائل برنامه نویسی دینامیک وجود ندارد. در واقع، برنامه‌نویسی دینامیک صرفاً یک روش برخورد کلی جهت حل این نوع مسائل در اختیار ما قرار می‌دهد و در هر مورد، باید معادلات و روابط ریاضی مخصوصی که با شرایط آن مسئله تطبیق دارد نوشته شود.

در این راهنما به بررسی یک مسئله برنامه‌نویسی دینامیک می‌پردازیم تا روش یافتن مسیرهای بهینه را معرفی کنیم. مسئله ما چنین است:

یک شبکه با اندازه N*M (یعنی N ردیف و M ستون) داریم. هر مربع در این شبکه می‌تواند با استفاده از یک جفت عدد صحیح (A,B) اندیس شود که 0≤A < N و 0≤B < M. یک ماشین در آغاز در فیلد (0,0) قرار دارد. این ماشین دو نوع حرکت می‌تواند انجام دهد:

• حرکت از فیلد (A,B) به فیلد (A+1,B)

یا

• حرکت از فیلد (A,B) به فیلد (A,B+1)

این ماشین در طی حرکت خود روی شبکه همه سکه‌هایی که در خانه‌های مسیرش قرار دارد را جمع می‌کند. اکنون مسئله چنین است:

یک تابع بنویسید که با فرض وجود یک ماتریس N*M، تعداد سکه‌های موجود در هر خانه یک شبکه با اندازه N*M را توصیف کرده و تعداد بیشینه سکه‌هایی که ماشین می‌تواند با حرکت از خانه (0, 0) به خانه (N−1, M−1) به روش توصیف شده در بالا جمع کند را بازگشت دهد.

نخستین راه‌حل

ما در نخستین تلاش خود برای حل این مسئله به کدی مانند زیر رسیدیم، هر چند حالت‌های خاص و مشابه آن‌ها در این کد لحاظ نشده‌اند:

function solutionAttempt(A){
 
 //First finding the values of P and Q
  const P= A.length
  const Q= A[0].length

  let x =0
  let y =0
  let total = A[0][0]+A[P-1][Q-1]

  while (x != P-1 && y != Q-1){

  
   if (A[x+1][y]>A[x][y+1]){
    x += 1
   }else{
    y +=1 
   }

  total += A[x][y]
 }

 return total   
    
}

البته موارد خاصی مانند رفتار ماشین هنگامی که x و y در لبه شبکه باشند نیز وجود دارند؛ اما برای ما که در ابتدای حل مسئله هستیم، این موارد چندان مهم نیستند. موارد نقص این راه‌حل را در کد فوق بررسی می‌کنیم و سعی می‌کنیم در گام بعدی آن‌ها را رفع کنیم.

چرا این راه‌حل خوب نیست؟

در راه‌حل فوق از الگوریتمی که به نام «الگوریتم حریصانه» (greedy algorithm) نامیده می‌شود، استفاده شده است. این الگوریتم در هر گام انتخاب بهینه را انجام می‌دهد و تلاش می‌کند تا روش بهینه کلی برای حل کل مسئله را بیابد. الگوریتم‌های حریصانه می‌توانند کاملاً موفق باشند؛ اما برخی نواقص مهم دارند.

برای نمونه از آنجا که الگوریتم حریصانه تلاش می‌کند مسیری را با انتخاب کردن بیشترین تعداد سکه‌های موجود در هر گام پیدا کند، بیشینه مجموع را از دست می‌دهد. این وضعیت در انیمیشن زیر نمایش یافته است. ضعف الگوریتم حریصانه آن است که تصمیم‌هایش را بدون در نظر گرفتن مسئله کلی می‌گیرد.

در سوی دیگر جنبه مثبت الگوریتم حریصانه این است که پیچیدگی زمانی کاملاً پایین حفظ شده است؛ اما با این که این راه‌حل کاملاً کارآمد است؛ اما این وضعیت جبران نتایج نادرستی که ارائه کرده است را نمی‌کند.

متد بازگشتی

معمولاً در زمان تست بهتر است از روش‌های بازگشتی اجتناب کنیم، دلیل این مسئله آن است که در زمان تست باید بیشترین عملکرد ممکن را داشته باشیم و راهبردهای مبتنی بر بازگشت منجر به پیچیدگی‌های زمانی نمایی می‌شوند، چون هر حالت باید مجدداً محاسبه شود. به علاوه اندازه پشته فراخوانی بسیار بزرگ خواهد شد. نمودار درختیِ همه حالت‌هایی را که باید برای یک ماتریس بزرگ ایجاد شود را تصور کنید که هر یک تابع را بار دیگر فراخوانی می‌کند.

با این باور که باید چیزی بین راه‌حل فوق و راه‌حل زیر را انتخاب کنیم باعث شد تا کدی شبیه به آنچه قبلاً دیدیم را بنویسیم. با این وجود، اگر می‌خواستیم یک راه‌حل بازگشتی بنویسیم، احتمالاً باید چیزی مانند قطعه کد زیر می‌نوشتیم:

function max_path(P,Q,A){
  let max_values = []
  if (A[P-1][Q] > A[P][Q-1]){
     max_values[P][Q]= A[P][Q] + max_path(P-1,Q,A)
  }else{
     max_values[P][Q]= A[P][Q] + max_path(P,Q-1,A)
   }

return max_values[P][Q]

}

در کد فوق ما به طور بازگشتی کوتاه‌ترین مسیر برای هر مربع را در ماتریس محاسبه می‌کنیم. این وضعیت را در ادامه بیشتر توضیح داده‌ایم، تنها تفاوت در این است که در تابع فوق، هر مقدار که قبلاً یافت شده است، در هر بار فراخوانی مجدد تابع، دوباره محاسبه می‌شود. با این وجود، یک رویکرد سوم نیز وجود دارد.

حل کردن مسئله با استفاده از برنامه‌نویسی دینامیک

در ابتدا به توضیح ماهیت برنامه‌نویسی دینامیک می‌پردازیم. برنامه‌نویسی دینامیک به این دلیل چنین نامگذاری شده است که مبدع آن، «ریچارد بلمن» (Richard Bellman) این عبارت را جالب تصور می‌کرده است!

به طور خلاصه می‌توان گفت که برنامه‌نویسی دینامیک به طور کلی یک تکنیک قدرتمند برای طراحی الگوریتم است. همچنین می‌توانیم برنامه‌نویسی دینامیک را نوعی «جستجوی جامع» (exhaustive search) به حساب آورد. به طور معمول این تصور که یک جستجوی جامع به پیچیدگی زمانی به صورت نمایی نیاز دارد، ایده نادرستی است. چون اگر به درستی از روش «brute force» استفاده کنید، می‌توانید پیچیدگی زمانی را از حالت نمایی تا حد چندجمله‌ای کاهش دهید. این وضعیت را قبلاً در الگوریتم حریصانه نیز مشاهده کردیم.

این تکنیک شامل «memoization» است که به نگهداری محاسبات مرتبط در حافظه گفته می‌شود. ایده کار در این روش تا حدودی شبیه داشتن یک چک‌نویس است. ما همه محاسبه‌ها را روی یک کاغذ می‌نویسیم و از نتایج محاسبه‌های قبلی نیز بهره می‌گیریم. راه‌حل‌هایی که روی چک‌نویس نوشته می‌شوند، به مسئله نهایی که به دنبال حل آن هستیم ربطی ندارند؛ بلکه مسائل فرعی هستند که قبلاً به روش بازگشتی آن‌ها را حل کرده‌ایم.

مثال ساده: دنباله فیبوناچی

در این بخش ابتدا یک پیاده‌سازی ساده از روش بازگشتی را معرفی می‌کنیم و در ادامه راه‌حل بازگشتی خود را برای مسئله ابتدایی این مقاله ارائه خواهیم کرد.

function fib(n)  {
  let array = [1, 1]         
  if (n === 0 || n === 1) {
    return 1 
  }
  for (let i= 2 ; i < n; i++) {
    array.push(array[0] + array[1])
    array.shift()
  }

  return array[0] + array[1];
}

طرز کار کد فوق از طریق ایجاد یک مبنای کد شناخته شده صورت می‌گیرد که اگر N=0 یا N=1 باشد، جمله نخست 1 خواهد بود. نتایج معلوم در آرایه ذخیره می‌شوند و سپس پردازش آغاز می‌شود.

1. اگر جمله n-اُم که به عنوان memo استفاده می‌شود، در آرایه ما قرار دارد، کافی است آن را بازگشت دهیم.
2. در غیر این صورت جمله بعدی را در دنباله محاسبه کرده و آن را به memo خود اضافه می‌کنیم.
3. مرحله 1 را تکرار می‌کنیم.

این بدان معنی است که ما هر نتیجه را تنها یک بار محاسبه می‌کنیم و دیگر نیاز نیست که محاسبات را بارها و بارها اجرا کنیم. به این ترتیب پیچیدگی مسئله مورد بررسی تا حد زیادی کاهش می‌یابد.

در عین این که می‌توانیم از «بازگشت» برای راه‌اندازی پردازش از هر جایی استفاده کنیم، می‌توانیم از عیب‌های آن نیز اجتناب کنیم. بدین ترتیب کار خود را با یک memo خالی آغاز می‌کنیم و تابع را پس از محاسبه و ثبت محاسبه نخست فراخوانی می‌کنیم، یعنی تابع باید دو بار فراخوانی شود.

بررسی مثال ماتریس دوبعدی

اینک به بررسی چگونگی استفاده از این راه‌حل در مورد مثال اولیه ماتریس پر از سکه خود می‌پردازیم. دقت کنید که این مسئله نکته‌ای دارد که در صورتی که ماشین هر کجا متوقف شده باشد، با بررسی کردن می‌توانیم بفهمیم که پاسخ چیست. اگر ماشین در مربع نخست یعنی [0][0] متوقف شده باشد و هرگز تکان نخورده باشد، در این صورت مربع‌های [A[0][0 را جمع‌آوری کرده است.

به بیان ساده این بدان معنی است که ما می‌دانیم که بیشینه تعداد سکه‌هایی که می‌توان بدون حرکت کردن به دست آورد تعداد سکه‌های موجود در مربع نخست است. بدین ترتیب این حالت مبنای ما است.

سپس باید ببینیم آیا می‌توان مسئله را به مسائل ساده‌تر تقسیم کرد یا نه. ما قبلاً این کار را هنگام کار با بازگشت انجام داده‌ایم. اگر بدانیم که بدون هیچ حرکتی در حالت بیشینه چه تعداد سکه داریم، می‌توانیم بیشینه تعداد سکه‌ها را پس از یک حرکت نیز بدانیم.

بیشینه تعداد سکه‌ها برای هر مربعی برابر با تعداد سکه‌های روی مربع به علاوه بیشینه تعداد سکه‌ها روی پرمنفعت‌ترین مربع‌های مجاور خواهد بود. برای تصور این حالت به نمودارهای زیر توجه کنید:

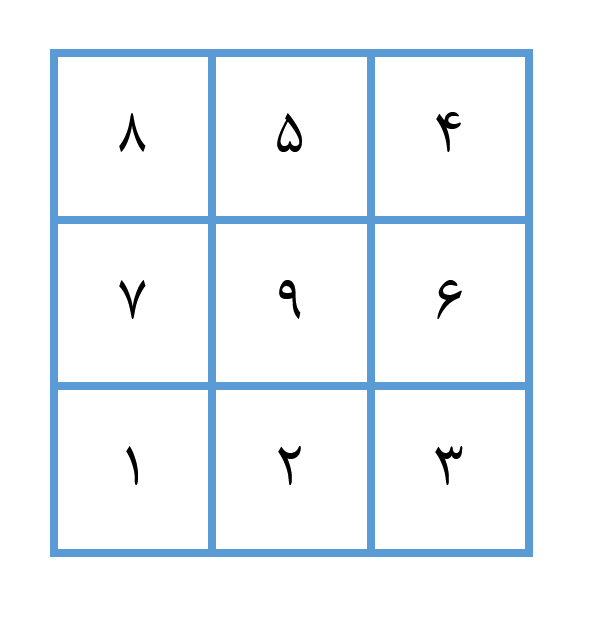
مربع چپ-پایین به صورت (0,0) و مربع بالا-چپ به صورت (2,2) است. اگر حرکت خود را از گوشه چپ-پایین آغاز کنیم و بخواهیم به گوشه راست-بالا به روش توصیف شده حرکت کنیم، مشخص است که قبل از حرکت نخست (زمانی که هنوز در مربع 0,0 هستیم) 1 سکه خواهیم داشت.

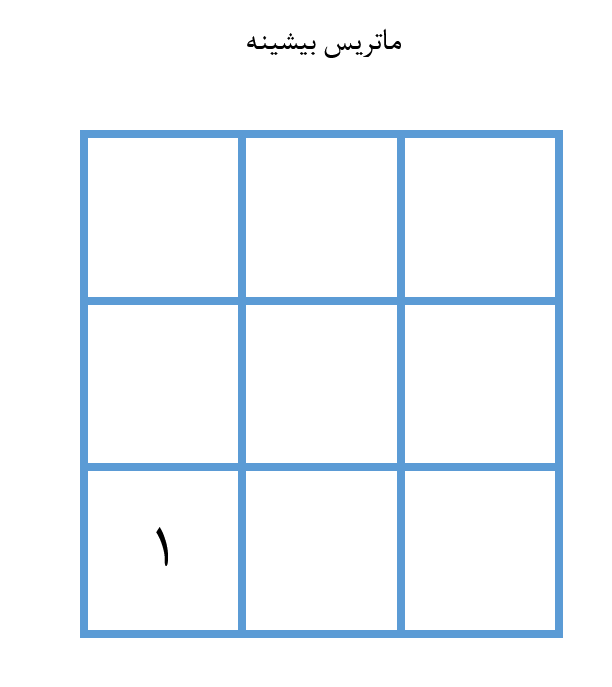
این مقدار را در memo ی خود ثبت می‌کنیم. بدین ترتیب یک ماتریس دیگر خواهیم داشت که در آن تعداد بیشینه ممکن از سکه‌ها را برای هر مربع ثبت خواهیم کرد. اکنون حالت مبنای خود را داریم و می‌دانیم که تعداد سکه‌ها در هر مربع چه قدر است. به این ترتیب با جمع کردن بیشینه تعداد ردیف پایین و ستون‌ها کار خود را ادامه می‌دهیم.

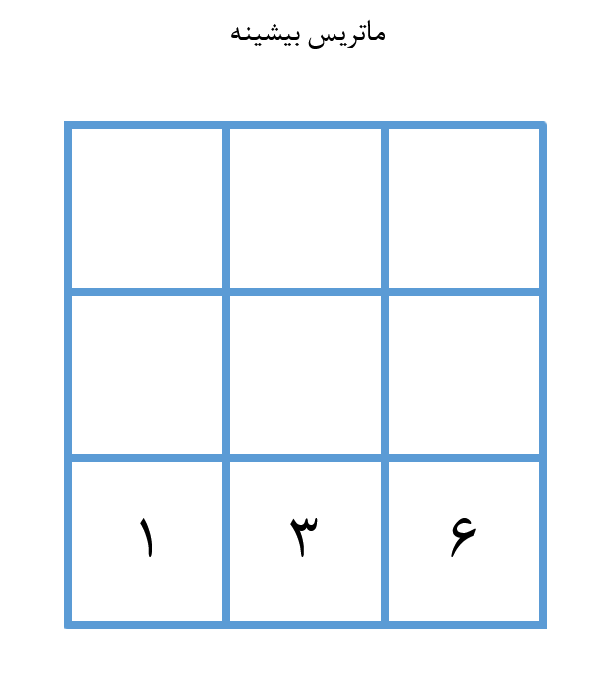
در ردیف پایین به سمت عرضی حرکت می‌کنیم و 2 سکه و 3 سکه موجود را جمع می‌کنیم. سپس این فرایند را در مورد ستون اول نیز تکرار می‌کنیم.

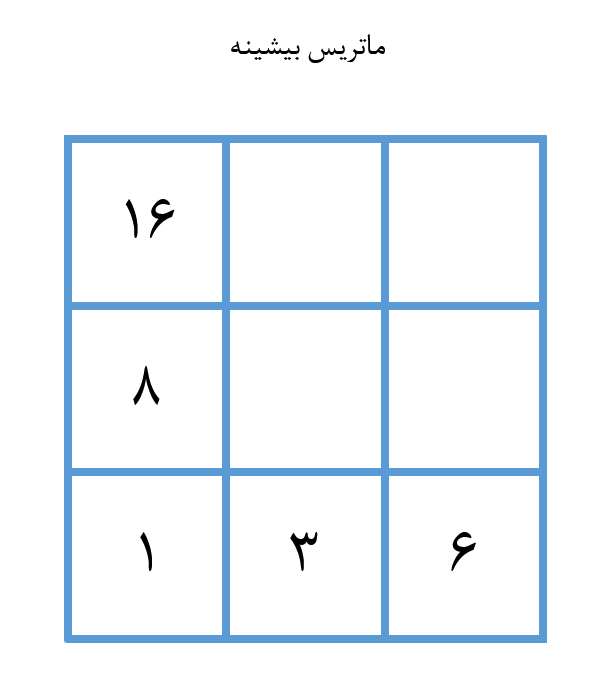
در نهایت ستون میانی را پر می‌کنیم تا به ماتریس زیر برسیم.

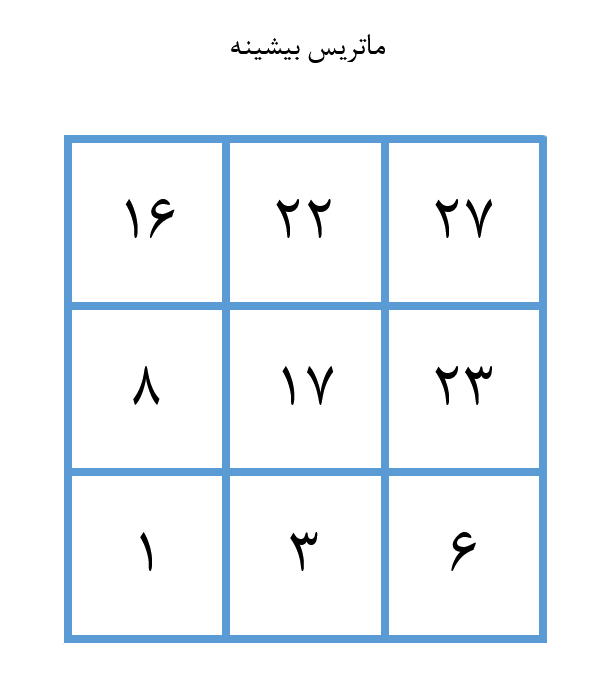
در این حالت می‌بینیم که بیشینه تعداد سکه‌ها برابر با 27 است. ما این کار را بدون استفاده از بازگشت انجام داده‌ایم، زیرا هرگز نتایج قبلی خود را مجدداً محاسبه نکرده‌ایم. کد آن به صورت زیر است:

function MaxCoins(A){

  //First finding the values of P and Q
  const x_axis = A.length
  const y_axis= A[0].length

  //setting up the "matrix of maximums"
  
  let memo=[]
  for (let i=0; i<x_axis ; i++){
     memo[i] = []
   }
   
  //Base Case
  memo[0][0] = A[0][0]

  //Bottom Row

  for (let i=1 ; i<x_axis; i++){
    memo[i][0] = memo[i-1][0]+A[i][0]
  }

  //Bottom Column

  for (let i=1 ; i<y_axis; i++){
    memo[0][i] = memo[0][i-1]+A[0][i]
  }

//Everywhere else
  for (let i=1; i<x_axis; i++){
    for (let k=1; k<y_axis; k++){
       if (memo[i-1][k]>memo[i][k-1]){
          memo[i][k] = memo[i-1][k]+A[i][k]
       }else {
          memo[i][k] = memo[i][k-1]+A[i][k]
       }
    }   
  }

  return memo[x_axis - 1][y_axis - 1 ]

 }

کد فوق مقدار 27 را بازگشت می‌دهد، که مورد انتظار است.

سخن پایانی

مسئله‌ای که در این نوشته بررسی کردیم ممکن است در ابتدا دشوار به نظر برسد؛ اما پس از کمی کار کردن متوجه می‌شویم که چگونه می‌توانیم به راه‌حلی برای آن دست یابیم. در این نوشته همه این مراحل را با هم مرور کردیم. بدین ترتیب با روش جدیدی برای حل مسائل به نام برنامه‌نویسی دینامیک آشنا شدیم.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های بهینه‌سازی کلاسیک و هوشمند
• آموزش یادگیری تقویتی – Reinforcement Learning
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• معرفی الگوریتم های مجانبی، حریصانه و برنامه‌ نویسی دینامیک — به زبان ساده
• آموزش ساختمان داده — مجموعه مقالات جامع وبلاگ فرادرس
• نمایش سیستم های دینامیکی با متلب — از صفر تا صد

==