الگوریتم های تقسیم و حل (Divide and Conquer Algorithms) – راهنمای مقدماتی

۵۷۸۷ بازدید

آخرین به‌روزرسانی: ۳ مرداد ۱۴۰۳

زمان مطالعه: ۶ دقیقه

دانلود PDF مقاله

یکی از الگوریتم‌های پرکاربرد در زمینه برنامه‌نویسی و همچنین حوزه‌های دیگر «الگوریتم‌های تقسیم و حل» (Divide and Conquer Algorithms) هستند. در این نوع الگوریتم تنها کاری که انجام می‌دهیم این است که مسائل را به مسئله‌های کوچک‌تر تجزیه می‌کنیم. از این نظر این الگوریتم‌ها شبیه روابط بازگشتی هستند؛ اما باید بدانیم که کجا باید این فرایند تقسیم کردن را متوقف کنیم. فرض کنید 8 عدد زیر را در اختیار داریم:

فهرست مطالب این نوشته

مرتب‌سازی ادغامی

برج‌های هانوی

اعداد فیبوناچی

4 6 3 2 8 7 5 1

و می‌خواهیم همه آن‌ها را با هم جمع کنیم. ما این مسئله را به 8 بخش تقسیم می‌کنیم که هر یک شامل یک مورد از این اعداد است:

4 6 3 2 8 7 5 1

سپس شروع به جمع زدن دو به دو اعداد می‌کنیم، در این حالت ما 4 جفت عدد به صورت زیر داریم:

4+6 3+2 8+7 5+1

این فرایند را به همین ترتیب ادامه می‌دهیم. شاید از خود بپرسید، چرا ما تقسیم کردن اعداد را تا زمانی که به 8 بخش مختلف رسیدیم ادامه دادیم و چرا زمانی که چهار جفت عدد داشتیم متوقف نشدیم تا دوباره یک مرحله دیگر برای رسیدن به این وضعیت طی نکنیم.

اگر ما تنها یک ورودی به صورت 1 داشته باشیم چطور؟ یا اگر تعداد اعداد ورودی ما فرد باشد چطور؟ ما باید تجزیه اعداد را تا زمانی که به عناصر منفرد نرسیده‌ایم ادامه دهیم تا با چنین وضعیت‌هایی مواجه نشویم. یک الگوریتم تقسیم و حل تلاش می‌کند که یک مسئله را تا حد امکان به بخش‌های کوچک‌تری تقسیم کند، چون حل مسائل کوچک‌تر، آسان‌تر است. این کار معمولاً به وسیله روابط بازگشتی صورت می‌گیرد.

نمونه‌هایی از «تقسیم و حل» شامل مرتب‌سازی ادغامی و محاسبه عدد فیبوناچی است. در ادامه شبه کد محاسبه عدد فیبوناچی را ملاحظه می‌کنید:

algorithm f(n)
if n == 0 or n == 1 then
   return 1
else
   f(n-1) + f(n+1)

مرتب‌سازی ادغامی

مرتب‌سازی ادغامی نوعی از الگوریتم‌های مرتب‌سازی (sort) است. طرز کار این الگوریتم تقریباً به صورت زیر است:

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

توالی n عدد را به دو نیمه تقسیم می‌کنیم.
به طور بازگشتی دو نیمه را مرتب می‌کنیم.
دو نیمه مرتب شده را دریک توالی مرتب منفرد ادغام می‌کنیم.

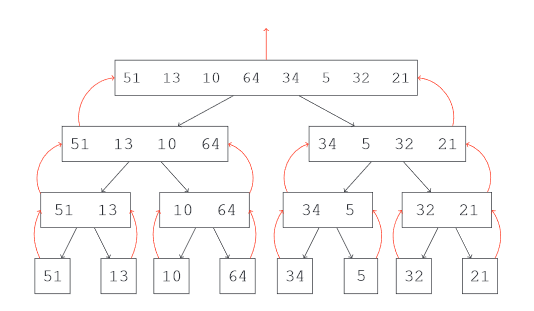
Merge Sort

در تصویر فوق ما 8 عدد را به اعداد منفرد تقسیم کردیم. زمانی که این کار صورت گرفت، فرایند مرتب‌سازی را آغاز می‌کنیم.

عدد 51 را با 13 مقایسه می‌کنیم و عدد کوچک‌تر را در سمت چپ و عدد بزرگ‌تر را در سمت راست قرار می‌دهیم. این کار را برای اعداد 10 و 64، 34 و 5، 32 و 21 نیز تکرار می‌کنیم.

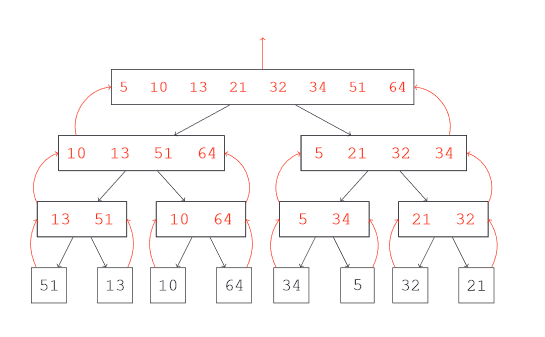
Merge Sort

ما این کار را برای سطوح بعد نیز انجام می‌دهیم تا به یک لیست کاملاً مرتب ادغام شده در سطح فوقانی دست یابیم. در سطح دوم از بالا یعنی زمانی که 2 نیمه هر کدام با 4 عدد داریم، 2 اشاره‌گر ایجاد می‌کنیم. اشاره‌گر شماره 1 به عدد 10 و اشاره‌گر شماره 2 به عدد 5 اشاره می‌کند.

در ادامه عدد 10 و 5 مقایسه می‌شود و چون 5 کوچک‌تر از 10 است، 5 به عنوان کوچک‌ترین عنصر در ابتدای لیست قرار می‌گیرد.

سپس عدد 10 و 21 مقایسه می‌شوند و چون 10 از 21 کوچک‌تر است و از آنجا که می دانیم 10 کوچک‌ترین آیتم در لیست اول است (این اطلاع از فرایند مرتب‌سازی و ادغام ما در مراحل قبلی ناشی می‌شود) از این رو 10 در ابتدای لیست و پس از 5 قرار می‌گیرد. این کار برای همه اعداد موجود انجام می‌یابد تا این که به یک لیست کاملاً مرتب منفرد دست پیدا کنیم.

لازم به ذکر است که ما 2 لیست از اعداد نامرتب را با هم مقایسه نمی‌کنیم؛ بلکه ما 2 لیست از اعداد مرتب را با هم مقایسه می‌کنیم. ما می دانیم که 10 در لیست سمت چپ کوچک‌ترین عدد است. ما می‌دانیم که 13 دومین عدد کوچک مرتب شده در لیست سمت چپ است.

Algorithm Merge_Sort(list)
if n > 1
   copy A[1...n/2] to B[1...n/2]
   copy A[(n/2 + 1)...n] to C[1...n/2]
   merge_sort(b)
   merge_sort(c)
   merge(b, c, a)
end

معیار ما در این کد n است. اگر n بزرگ‌تر از 1 باشد در این صورت باید مسئله را باز هم تجزیه کرده و حل کنیم. اگر n برابر با 1 باشد، اگر 1 آیتم در آرایه باشد در این صورت آرایه هم اینک مرتب است.

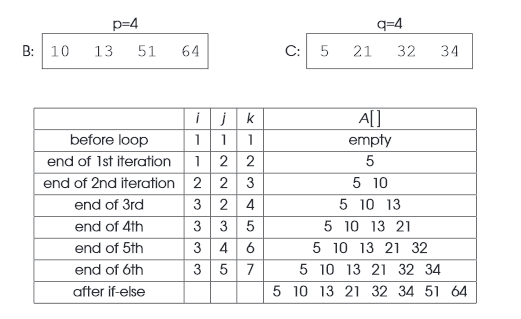
trace table

به جدول اثر فوق توجه کنید ما در این جدول 2 لیست داریم که هر یک شامل 4 آیتم هستند. این لیست‌ها مرتب‌سازی شده‌اند. ما می‌خواهیم آن‌ها را ادغام کنیم. i یک اشاره‌گر در لیست اول یعنی B است. j یک اشاره‌گر در لیست دوم یعنی C است. K همان k-امین عنصر در لیست مرتب‌سازی شده جدید است.

دقت کنید که چگونه عناصر را مانند مثال‌های قبلی این نوشته با هم مقایسه می‌کنیم. هر گره به زمانی برابر با (O(p نیاز دارد که p تعداد عناصر موجود در لیست است.

هر سطح به زمانی برابر با (O(n نیاز دارد، زیرا تعداد کل اعداد صحیحی در هر سطح برابر با n است. در کل (O(log n سطح وجود دارد و از این رو زمان کلی برای اجرای این الگوریتم برابر با (O(n log n است.

برج‌های هانوی

برج‌های هانوی یک مسئله ریاضیاتی است که شامل 3 میله و چند دیسک است. ما در مثال خود از 3 دیسک استفاده می‌کنیم.

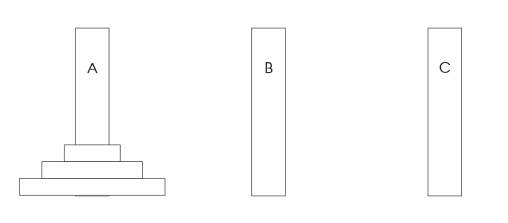
هر دیسک اندازه متفاوتی دارد. ما می‌خواهم همه دیسک‌ها را به میله C انتقال دهیم به طوری که بزرگ‌ترین دیسک در پایین، دیسک متوسط در میانه و دیسک کوچک‌تر در سطح بالایی قرار بگیرد.

ما هر بار تنها 1 دیسک را می‌توانیم جا به جا کنیم. یک دیسک نمی‌تواند روی دیسک‌هایی که کوچک‌تر از خود است قرار بگیرد. اگر 1 دیسک داشته باشیم، کافی است آن را به میله C انتقال دهیم. اگر 2 دیسک داشته باشیم، این مسئله با 3 حرکت به صورت زیر حل می‌شود که ابتدا کوچک‌ترین دیسک را در میله بافر قرار دهیم (1 حرکت). سپس بزرگ‌ترین دیسک را به میله C انتقال می‌دهیم (2 حرکت) و در نهایت دیسک بافر را به میله C منتقل می‌کنیم (3 حرکت).

زمانی که 4 دیسک داشته باشیم، برای حل این مسئله به 15 حرکت نیاز خواهیم داشت. در مورد 5 دیسک این عدد به 31 می‌رسد.

در واقع فرمول تعداد حرکت‌های مورد نیاز به صورت توان‌های 2 منهای 1 است. برای حل هر مسئله برج‌های هانوی با تعداد دیسک n، به $(2^n) - 1$ حرکت نیاز داریم. دقت کنید که برای حل این مسئله به یک میله بافر نیاز داریم. اگر بخواهیم این وضعیت را تعمیم دهیم به صورت زیر عمل می‌کنیم:

وقتی n دیسک داریم، n-1 دیسک را از میله A به میله B انتقال می‌دهیم، بزرگ‌ترین را از A به C انتقال می‌دهیم و سپس به طور بازگشتی n-1 دیسک را از میله B به میله C انتقال می‌دهیم.

اگر تعداد دیسک‌ها عددی زوج باشد، حرکت اول همواره به میله میانی خواهد بود. اگر تعداد دیسک‌ها عددی فرد باشد اولین حرکت همواره به میله سمت دیگر خواهد بود.

ToH(numDisc, source, destination, spare)
if (numDisc > 1)
    ToH(numDisc-1, source, spare, destination)

Move a disc from source to destination

if (numDisc > 1)
    ToH(numDisc-1, spare, destination, source)

تصویر زیر درخت اجرای الگوریتم فوق را با (ToH(3, A, C, B نشان می‌دهد.

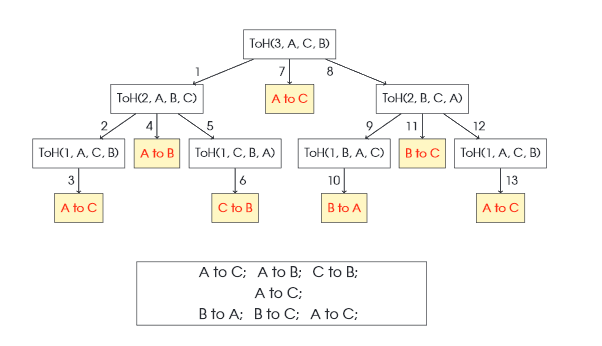
algorithm

زمانی که آن را فراخوانی می‌کنیم، 2 فراخوانی به موارد زیر داریم:

(ToH(2, A, B, C
(ToH(2, B, C, A

از آنجا که 2 بزرگ‌تر از 1 است، آن را باز هم یک سطح به سمت پایین منتقل می‌کنیم.

اعداد فیبوناچی

اعداد فیبوناچی را می‌توان در طبیعت مشاهده کرد.

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

این اعداد از 1 آغاز می‌شوند و عدد بعدی برابر با عدد کنونی + عدد قبلی است. در این مورد عدد دوم به صورت 2 = 1 + 1 است. سپس عدد سوم به صورت 3 = 1 + 2 و همین طور 5 = 2 + 3 است و این روند تا به آخر ادامه می‌یابد.

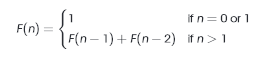
Fibonacci Numbers

این تعریف رسمی اعداد فیبوناچی است. اگر n=0 یا n=1 باشد، خروجی 1 خواهد بود و در غیر این صورت مجموع اعداد قبلی با عدد کنونی جمع می‌شود.

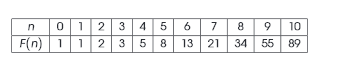
الگوریتم محاسبه اعداد فیبوناچی به صورت زیر است:

Algorithm F(n)

if n == 0 or n == 1 then
   return 1
else
   return F(n-1)+F(n-2)

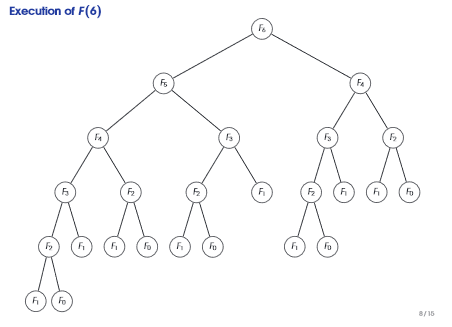
Fibonacci Numbers

در مثال فوق N برابر با 6 است. از آنجا که N بزرگ‌تر از 0 یا 1 است، آن بخش را نادیده می‌گیریم. سپس (F(5) + F(4 را محاسبه می‌کنیم. (F(5 به صورت جمع (F(4) + F(2 محاسبه می‌شود.

در نهایت وقتی به حالت‌های پایه برسیم که F برابر با 0 یا 1 باشد، اعداد 1 را خواهیم داشت. در هر مرحله عدد قبلی را به مرحله بالاتر بازگشت می‌دهیم. بنابراین محاسبه زیر را خواهیم داشت:

F(1) + F(0) = 2

و سپس

F2 + F1 = 2 + 1 = 3

بدین ترتیب به انتهای این نوشته با موضوع آشنایی با الگوریتم‌های تقسیم و حل می‌رسیم. اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

محصول، خدمات یا برند خود را در مجله فرادرس معرفی کنید.

کلیک کنید

بر اساس رای ۱۵ نفر

آیا این مطلب برای شما مفید بود؟

اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.

ثبت نظر

منابع:

brandons-computer-science-notes

میثم لطفی (+)

«میثم لطفی» در رشته‌های ریاضیات کاربردی و مهندسی کامپیوتر به تحصیل پرداخته و شیفته فناوری است. وی در حال حاضر علاوه بر پیگیری علاقه‌مندی‌هایش در رشته‌های برنامه‌نویسی، کپی‌رایتینگ و محتوای چندرسانه‌ای، در زمینه نگارش مقالاتی با محوریت نرم‌افزار با مجله فرادرس همکاری دارد.