الگوریتم پریم — به زبان ساده

«الگوریتم پریم» (Prim’s Algorithm)، یک الگوریتم «حریصانه» (Greedy) است. این الگوریتم، با یک درخت پوشای کمینه (Minimum Spanning Tree | MST) خالی آغاز به کار می‌کند. هدف آن است که دو مجموعه از راس‌ها ساخته شوند. اولین مجموعه، شامل راس‌هایی است که در حال حاضر در درخت پوشای کمینه قرار دارند. مجموعه دیگر، شامل راس‌هایی است که هنوز در درخت قرار ندارند. در هر گام، الگوریتم همه یال‌هایی که دو مجموعه را به یکدیگر متصل می‌کنند در نظر می‌گیرد و یال دارای حداقل وزن را از میان این یال‌ها برمی‌گزیند. پس از انتخاب یال، دیگر نقطه نهایی یال را به پوشه حاوی راس‌های MST انتقال می‌دهد.

در «نظریه گراف» (Graph Theory)، به گروهی از یال‌ها که دو مجموعه از راس‌ها را در گراف به یکدیگر متصل می‌کنند «برش» (Cut) گفته می‌شود. بنابراین، در هر گام از الگوریتم پریم، می‌توان برشی را پیدا (از دو مجموعه، یکی حاوی یال‌هایی که در حال حاضر در MST قرار دارند و دیگری حاوی سایر راس‌ها است) و یال با کمترین وزن را از برش انتخاب کرد و در مجموعه MST قرار داد (مجموعه حاوی راس‌هایی است که در حال حاضر در درخت پوشای کمینه پریم قرار دارند). در ادامه، روش کار الگوریتم پریم مورد بررسی قرار گرفته و سپس، کد پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون شامل ++C ،C، «جاوا» (Java)، «پایتون» (Python) و «سی‌شارپ» (#C) ارائه شده است.

روش کار الگوریتم پریم

ایده نهفته در پس الگوریتم پریم ساده است. درخت پوشا یعنی همه راس‌ها باید به یکدیگر متصل باشند. بنابراین، دو مجموعه مجزا (که در بالا تشریح شدند) باید برای ساخت یک درخت پوشا به یکدیگر متصل شوند. همچنین، باید با یال‌های دارای حداقل وزن به یکدیگر متصل شوند تا درخت پوشای کمینه ساخته شود.

فیلم آموزش مبانی برنامه نویسی – الگوریتم و فلوچارت با رویکرد حل مساله در فرادرس

کلیک کنید

الگوریتم پریم

1. مجموعه mstSet را بساز که راس‌هایی که در حال حاضر در درخت پوشای کمینه پریم وجود دارند در آن قرار دارد.
2. یک مقدار کلیدی را به همه راس‌ها در گراف ورودی تخصیص بده. همه مقادیر کلیدی را با INFINITE مقداردهی اولیه کن. مقدار کلیدی صفر (۰) را به اولین راس تخصیص بده، تا این راس در ابتدا انتخاب شود.
3. تا هنگامی که mstSet حاوی همه راس‌ها نیست:
   • راس u را که در mstSet قرار ندارد و کمترین مقدار کلیدی را دارا است انتخاب کن.
   • u را در mstSet قرار بده.
   • مقادیر کلیدی همه راس‌های مجاوری u را به روز رسانی کن. برای به روز رسانی این مقادیر کلیدی، در همه راس‌های مجاور تکرار را انجام بده. برای هر راس مجاور v، اگر وزن یال u-v کمتر از مقدار کلیدی پیشین v است، مقادیر کلیدی را به عنوان وزن u-v به روز رسانی کن.

هدف از استفاده از مقادیر کلیدی، انتخاب یال دارای کمترین وزن از برش است. مقادیر کلیدی تنها برای راس‌هایی استفاده می‌شوند که در MST قرار ندارند، مقدار کلیدی برای این راس‌ها نشان‌گر حداقل وزنی است که آن‌ها را به مجموعه قرار داده شده در MST متصل می‌کند. برای درک بهتر موضوع، در ادامه مثالی ارائه شده است. گراف زیر با ۸ راس مفروض است.

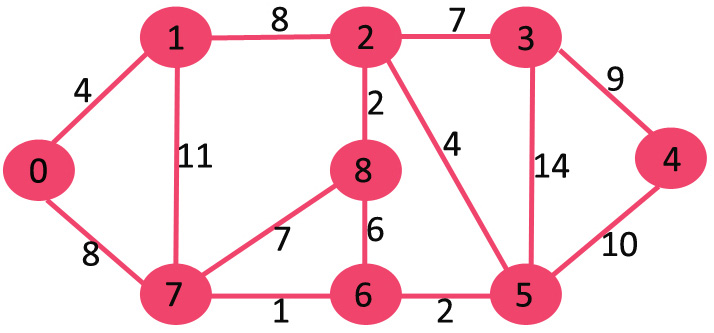
مجموعه mstSet به صورت اولیه خالی است و کلیدهای تخصیص پیدا کرده به راس‌ها به صورت $$ \{ 0, INF, INF, INF, INF, INF, INF, INF \} $$ هستند؛ INF در این مجموعه به معنای نامتناهی است. اکنون، راسی با کمترین مقدار کلیدی انتخاب می‌شود. راس ۰ انتخاب می‌شود که در mstSet قرار ندارد. پس از قرار دادن ۰ در مجموعه mstSet، مقادیر کلیدی راس‌های مجاور آن به روز رسانی می‌شوند. راس‌های مجاور ۰، راس‌های ۱ و ۷ هستند. مقادیر کلیدی ۱ و ۷ با ۴ و ۸ به روز رسانی می‌شوند. زیرگراف زیر، نشانگر راس‌ها و مقادیر کلیدی آن‌ها است. در شکل زیر، تنها راس‌هایی با مقادیر کلیدی متناهی نمایش داده شده‌اند. راس‌هایی که در MST قرار دارند، به رنگ سبز نمایش داده شده‌اند.

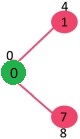
راسی با حداقل مقدار کلیدی که در حال حاضر در MST (درخت پوشای کمینه) قرار ندارد (در مجموعه mstSET قرار ندارد) و دارای وزن کمترین است (مقدار کلیدی) انتخاب می‌شود. بنابراین، در این وهله، راس 1 انتخاب و به mstSet اضافه می‌شود. بنابراین، mstSet اکنون به صورت {0, 1} است. مقادیر کلیدی از راس‌های مجاور ۱ به روز رسانی می‌شوند. مقدار کلیدی راس ۲ برابر با ۸ است.

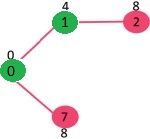
راسی با حداقل مقدار کلیدی که در حال حاضر در MST قرار ندارد (در mstSET قرار ندارد) انتخاب می‌شود. همچنین، می‌توان راس ۷ یا ۲ را انتخاب کرد. در حال حاضر، راس ۷ انتخاب می‌شود. بنابراین، mstSet اکنون به صورت $${0, 1, 7}$$ خواهد بود. مقادیر کلیدی راس‌های مجاور ۷ به روز رسانی می‌شوند. مقدار کلیدی راس‌های ۶ و ۸ متناهی می‌شوند (به ترتیب ۱ و ۷).

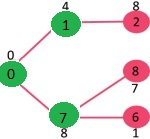
راس با حداقل مقدار کلیدی که در حال حاضر در MST قرار ندارد (در mstSET قرار ندارد) انتخاب می‌شود. بنابراین، mstSet اکنون به صورت {0, 1, 7, 6} خواهد بود. مقدار کلیدهای راس‌های مجاور به روز رسانی می‌شود. مقدار کلیدی راس ۵ و ۸ به روز رسانی می‌شود.

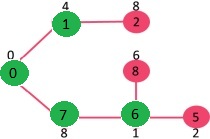
گام‌های بالا، تا هنگامی که mstSet شامل همه راس‌های گراف نشده است، ادامه خواهد داشت. در نهایت، گراف زیر حاصل خواهد شد.

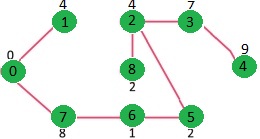
برنامه الگوریتم پریم

از یک آرایه بولی []mstSet برای ارائه مجموعه‌ای از راس‌هایی که در درخت پوشای کمینه قرار دارند استفاده می‌شود. اگر مقدار [mstSet[v درست (True) باشد، راس v در MST قرار دارد، در غیر این صورت، در درخت پوشای کمینه نیست. کلید آرایه []key برای ذخیره‌سازی مقادیر کلیدی همه راس‌ها مورد استفاده قرار می‌گیرد. آرایه دیگر []parent برای ذخیره‌سازی اندیس‌های راس‌های (گره‌های) والد در MST مورد استفاده قرار می‌گیرد. آرایه والد، آرایه خروجی است که برای نمایش درخت پوشای کمینه (MST) ساخته شده مورد استفاده قرار می‌گیرد.

برنامه الگوریتم پریم در ++C

فیلم آموزش ساختمان داده ها و پیاده سازی در سی پلاس پلاس C++‎ در فرادرس

کلیک کنید

// A C++ program for Prim's Minimum  
// Spanning Tree (MST) algorithm. The program is  
// for adjacency matrix representation of the graph  
#include <bits/stdc++.h> 
using namespace std; 
  
// Number of vertices in the graph  
#define V 5  
  
// A utility function to find the vertex with  
// minimum key value, from the set of vertices  
// not yet included in MST  
int minKey(int key[], bool mstSet[])  
{  
    // Initialize min value  
    int min = INT_MAX, min_index;  
  
    for (int v = 0; v < V; v++)  
        if (mstSet[v] == false && key[v] < min)  
            min = key[v], min_index = v;  
  
    return min_index;  
}  
  
// A utility function to print the  
// constructed MST stored in parent[]  
int printMST(int parent[], int graph[V][V])  
{  
    cout<<"Edge \tWeight\n";  
    for (int i = 1; i < V; i++)  
        cout<<parent[i]<<" - "<<i<<" \t"<<graph[i][parent[i]]<<" \n";  
}  
  
// Function to construct and print MST for  
// a graph represented using adjacency  
// matrix representation  
void primMST(int graph[V][V])  
{  
    // Array to store constructed MST  
    int parent[V];  
      
    // Key values used to pick minimum weight edge in cut  
    int key[V];  
      
    // To represent set of vertices not yet included in MST  
    bool mstSet[V];  
  
    // Initialize all keys as INFINITE  
    for (int i = 0; i < V; i++)  
        key[i] = INT_MAX, mstSet[i] = false;  
  
    // Always include first 1st vertex in MST.  
    // Make key 0 so that this vertex is picked as first vertex.  
    key[0] = 0;  
    parent[0] = -1; // First node is always root of MST  
  
    // The MST will have V vertices  
    for (int count = 0; count < V - 1; count++) 
    {  
        // Pick the minimum key vertex from the  
        // set of vertices not yet included in MST  
        int u = minKey(key, mstSet);  
  
        // Add the picked vertex to the MST Set  
        mstSet[u] = true;  
  
        // Update key value and parent index of  
        // the adjacent vertices of the picked vertex.  
        // Consider only those vertices which are not  
        // yet included in MST  
        for (int v = 0; v < V; v++)  
  
            // graph[u][v] is non zero only for adjacent vertices of m  
            // mstSet[v] is false for vertices not yet included in MST  
            // Update the key only if graph[u][v] is smaller than key[v]  
            if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])  
                parent[v] = u, key[v] = graph[u][v];  
    }  
  
    // print the constructed MST  
    printMST(parent, graph);  
}  
  
// Driver code 
int main()  
{  
    /* Let us create the following graph  
        2 3  
    (0)--(1)--(2)  
    | / \ |  
    6| 8/ \5 |7  
    | / \ |  
    (3)-------(4)  
            9    */
    int graph[V][V] = { { 0, 2, 0, 6, 0 },  
                        { 2, 0, 3, 8, 5 },  
                        { 0, 3, 0, 0, 7 },  
                        { 6, 8, 0, 0, 9 },  
                        { 0, 5, 7, 9, 0 } };  
  
    // Print the solution  
    primMST(graph);  
  
    return 0;  
}  
  
// This code is contributed by rathbhupendra

برنامه الگوریتم پریم در C

// A C program for Prim's Minimum 
// Spanning Tree (MST) algorithm. The program is 
// for adjacency matrix representation of the graph 
#include <limits.h> 
#include <stdbool.h> 
#include <stdio.h> 
// Number of vertices in the graph 
#define V 5 
  
// A utility function to find the vertex with 
// minimum key value, from the set of vertices 
// not yet included in MST 
int minKey(int key[], bool mstSet[]) 
{ 
    // Initialize min value 
    int min = INT_MAX, min_index; 
  
    for (int v = 0; v < V; v++) 
        if (mstSet[v] == false && key[v] < min) 
            min = key[v], min_index = v; 
  
    return min_index; 
} 
  
// A utility function to print the 
// constructed MST stored in parent[] 
int printMST(int parent[], int graph[V][V]) 
{ 
    printf("Edge \tWeight\n"); 
    for (int i = 1; i < V; i++) 
        printf("%d - %d \t%d \n", parent[i], i, graph[i][parent[i]]); 
} 
  
// Function to construct and print MST for 
// a graph represented using adjacency 
// matrix representation 
void primMST(int graph[V][V]) 
{ 
    // Array to store constructed MST 
    int parent[V]; 
    // Key values used to pick minimum weight edge in cut 
    int key[V]; 
    // To represent set of vertices not yet included in MST 
    bool mstSet[V]; 
  
    // Initialize all keys as INFINITE 
    for (int i = 0; i < V; i++) 
        key[i] = INT_MAX, mstSet[i] = false; 
  
    // Always include first 1st vertex in MST. 
    // Make key 0 so that this vertex is picked as first vertex. 
    key[0] = 0; 
    parent[0] = -1; // First node is always root of MST 
  
    // The MST will have V vertices 
    for (int count = 0; count < V - 1; count++) { 
        // Pick the minimum key vertex from the 
        // set of vertices not yet included in MST 
        int u = minKey(key, mstSet); 
  
        // Add the picked vertex to the MST Set 
        mstSet[u] = true; 
  
        // Update key value and parent index of 
        // the adjacent vertices of the picked vertex. 
        // Consider only those vertices which are not 
        // yet included in MST 
        for (int v = 0; v < V; v++) 
  
            // graph[u][v] is non zero only for adjacent vertices of m 
            // mstSet[v] is false for vertices not yet included in MST 
            // Update the key only if graph[u][v] is smaller than key[v] 
            if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v]) 
                parent[v] = u, key[v] = graph[u][v]; 
    } 
  
    // print the constructed MST 
    printMST(parent, graph); 
} 
  
// driver program to test above function 
int main() 
{ 
    /* Let us create the following graph 
        2 3 
    (0)--(1)--(2) 
    | / \ | 
    6| 8/ \5 |7 
    | /     \ | 
    (3)-------(4) 
            9         */
    int graph[V][V] = { { 0, 2, 0, 6, 0 }, 
                        { 2, 0, 3, 8, 5 }, 
                        { 0, 3, 0, 0, 7 }, 
                        { 6, 8, 0, 0, 9 }, 
                        { 0, 5, 7, 9, 0 } }; 
  
    // Print the solution 
    primMST(graph); 
  
    return 0; 
}

برنامه الگوریتم پریم در جاوا

فیلم آموزش الگوریتم ها و روش های جست و جو در آرایه (رایگان) در فرادرس

کلیک کنید

// A Java program for Prim's Minimum Spanning Tree (MST) algorithm. 
// The program is for adjacency matrix representation of the graph 
  
import java.util.*; 
import java.lang.*; 
import java.io.*; 
  
class MST { 
    // Number of vertices in the graph 
    private static final int V = 5; 
  
    // A utility function to find the vertex with minimum key 
    // value, from the set of vertices not yet included in MST 
    int minKey(int key[], Boolean mstSet[]) 
    { 
        // Initialize min value 
        int min = Integer.MAX_VALUE, min_index = -1; 
  
        for (int v = 0; v < V; v++) 
            if (mstSet[v] == false && key[v] < min) { 
                min = key[v]; 
                min_index = v; 
            } 
  
        return min_index; 
    } 
  
    // A utility function to print the constructed MST stored in 
    // parent[] 
    void printMST(int parent[], int graph[][]) 
    { 
        System.out.println("Edge \tWeight"); 
        for (int i = 1; i < V; i++) 
            System.out.println(parent[i] + " - " + i + "\t" + graph[i][parent[i]]); 
    } 
  
    // Function to construct and print MST for a graph represented 
    // using adjacency matrix representation 
    void primMST(int graph[][]) 
    { 
        // Array to store constructed MST 
        int parent[] = new int[V]; 
  
        // Key values used to pick minimum weight edge in cut 
        int key[] = new int[V]; 
  
        // To represent set of vertices not yet included in MST 
        Boolean mstSet[] = new Boolean[V]; 
  
        // Initialize all keys as INFINITE 
        for (int i = 0; i < V; i++) { 
            key[i] = Integer.MAX_VALUE; 
            mstSet[i] = false; 
        } 
  
        // Always include first 1st vertex in MST. 
        key[0] = 0; // Make key 0 so that this vertex is 
        // picked as first vertex 
        parent[0] = -1; // First node is always root of MST 
  
        // The MST will have V vertices 
        for (int count = 0; count < V - 1; count++) { 
            // Pick thd minimum key vertex from the set of vertices 
            // not yet included in MST 
            int u = minKey(key, mstSet); 
  
            // Add the picked vertex to the MST Set 
            mstSet[u] = true; 
  
            // Update key value and parent index of the adjacent 
            // vertices of the picked vertex. Consider only those 
            // vertices which are not yet included in MST 
            for (int v = 0; v < V; v++) 
  
                // graph[u][v] is non zero only for adjacent vertices of m 
                // mstSet[v] is false for vertices not yet included in MST 
                // Update the key only if graph[u][v] is smaller than key[v] 
                if (graph[u][v] != 0 && mstSet[v] == false && graph[u][v] < key[v]) { 
                    parent[v] = u; 
                    key[v] = graph[u][v]; 
                } 
        } 
  
        // print the constructed MST 
        printMST(parent, graph); 
    } 
  
    public static void main(String[] args) 
    { 
        /* Let us create the following graph 
        2 3 
        (0)--(1)--(2) 
        | / \ | 
        6| 8/ \5 |7 
        | /     \ | 
        (3)-------(4) 
            9         */
        MST t = new MST(); 
        int graph[][] = new int[][] { { 0, 2, 0, 6, 0 }, 
                                      { 2, 0, 3, 8, 5 }, 
                                      { 0, 3, 0, 0, 7 }, 
                                      { 6, 8, 0, 0, 9 }, 
                                      { 0, 5, 7, 9, 0 } }; 
  
        // Print the solution 
        t.primMST(graph); 
    } 
} 
// This code is contributed by Aakash Hasija

برنامه الگوریتم پریم در پایتون

فیلم آموزش نکات برنامه نویسی پایتون و حل مسائل الگوریتمی در فرادرس

کلیک کنید

# A Python program for Prim's Minimum Spanning Tree (MST) algorithm. 
# The program is for adjacency matrix representation of the graph 
  
import sys # Library for INT_MAX 
  
class Graph(): 
  
    def __init__(self, vertices): 
        self.V = vertices 
        self.graph = [[0 for column in range(vertices)]  
                    for row in range(vertices)] 
  
    # A utility function to print the constructed MST stored in parent[] 
    def printMST(self, parent): 
        print "Edge \tWeight"
        for i in range(1, self.V): 
            print parent[i], "-", i, "\t", self.graph[i][ parent[i] ] 
  
    # A utility function to find the vertex with  
    # minimum distance value, from the set of vertices  
    # not yet included in shortest path tree 
    def minKey(self, key, mstSet): 
  
        # Initilaize min value 
        min = sys.maxint 
  
        for v in range(self.V): 
            if key[v] < min and mstSet[v] == False: 
                min = key[v] 
                min_index = v 
  
        return min_index 
  
    # Function to construct and print MST for a graph  
    # represented using adjacency matrix representation 
    def primMST(self): 
  
        # Key values used to pick minimum weight edge in cut 
        key = [sys.maxint] * self.V 
        parent = [None] * self.V # Array to store constructed MST 
        # Make key 0 so that this vertex is picked as first vertex 
        key[0] = 0 
        mstSet = [False] * self.V 
  
        parent[0] = -1 # First node is always the root of 
  
        for cout in range(self.V): 
  
            # Pick the minimum distance vertex from  
            # the set of vertices not yet processed.  
            # u is always equal to src in first iteration 
            u = self.minKey(key, mstSet) 
  
            # Put the minimum distance vertex in  
            # the shortest path tree 
            mstSet[u] = True
  
            # Update dist value of the adjacent vertices  
            # of the picked vertex only if the current  
            # distance is greater than new distance and 
            # the vertex in not in the shotest path tree 
            for v in range(self.V): 
                # graph[u][v] is non zero only for adjacent vertices of m 
                # mstSet[v] is false for vertices not yet included in MST 
                # Update the key only if graph[u][v] is smaller than key[v] 
                if self.graph[u][v] > 0 and mstSet[v] == False and key[v] > self.graph[u][v]: 
                        key[v] = self.graph[u][v] 
                        parent[v] = u 
  
        self.printMST(parent) 
  
g = Graph(5) 
g.graph = [ [0, 2, 0, 6, 0], 
            [2, 0, 3, 8, 5], 
            [0, 3, 0, 0, 7], 
            [6, 8, 0, 0, 9], 
            [0, 5, 7, 9, 0]] 
  
g.primMST(); 
  
# Contributed by Divyanshu Mehta

برنامه الگوریتم پریم در #C

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

// A C# program for Prim's Minimum 
// Spanning Tree (MST) algorithm. 
// The program is for adjacency 
// matrix representation of the graph 
using System; 
class MST { 
  
    // Number of vertices in the graph 
    static int V = 5; 
  
    // A utility function to find 
    // the vertex with minimum key 
    // value, from the set of vertices 
    // not yet included in MST 
    static int minKey(int[] key, bool[] mstSet) 
    { 
  
        // Initialize min value 
        int min = int.MaxValue, min_index = -1; 
  
        for (int v = 0; v < V; v++) 
            if (mstSet[v] == false && key[v] < min) { 
                min = key[v]; 
                min_index = v; 
            } 
  
        return min_index; 
    } 
  
    // A utility function to print 
    // the constructed MST stored in 
    // parent[] 
    static void printMST(int[] parent, int[, ] graph) 
    { 
        Console.WriteLine("Edge \tWeight"); 
        for (int i = 1; i < V; i++) 
            Console.WriteLine(parent[i] + " - " + i + "\t" + graph[i, parent[i]]); 
    } 
  
    // Function to construct and 
    // print MST for a graph represented 
    // using adjacency matrix representation 
    static void primMST(int[, ] graph) 
    { 
  
        // Array to store constructed MST 
        int[] parent = new int[V]; 
  
        // Key values used to pick 
        // minimum weight edge in cut 
        int[] key = new int[V]; 
  
        // To represent set of vertices 
        // not yet included in MST 
        bool[] mstSet = new bool[V]; 
  
        // Initialize all keys 
        // as INFINITE 
        for (int i = 0; i < V; i++) { 
            key[i] = int.MaxValue; 
            mstSet[i] = false; 
        } 
  
        // Always include first 1st vertex in MST. 
        // Make key 0 so that this vertex is 
        // picked as first vertex 
        // First node is always root of MST 
        key[0] = 0; 
        parent[0] = -1; 
  
        // The MST will have V vertices 
        for (int count = 0; count < V - 1; count++) { 
  
            // Pick thd minimum key vertex 
            // from the set of vertices 
            // not yet included in MST 
            int u = minKey(key, mstSet); 
  
            // Add the picked vertex 
            // to the MST Set 
            mstSet[u] = true; 
  
            // Update key value and parent 
            // index of the adjacent vertices 
            // of the picked vertex. Consider 
            // only those vertices which are 
            // not yet included in MST 
            for (int v = 0; v < V; v++) 
  
                // graph[u][v] is non zero only 
                // for adjacent vertices of m 
                // mstSet[v] is false for vertices 
                // not yet included in MST Update 
                // the key only if graph[u][v] is 
                // smaller than key[v] 
                if (graph[u, v] != 0 && mstSet[v] == false
                    && graph[u, v] < key[v]) { 
                    parent[v] = u; 
                    key[v] = graph[u, v]; 
                } 
        } 
  
        // print the constructed MST 
        printMST(parent, graph); 
    } 
  
    // Driver Code 
    public static void Main() 
    { 
  
        /* Let us create the following graph 
        2 3 
        (0)--(1)--(2) 
        | / \ | 
        6| 8/ \5 |7 
        | / \ | 
        (3)-------(4) 
            9 */
  
        int[, ] graph = new int[, ] { { 0, 2, 0, 6, 0 }, 
                                      { 2, 0, 3, 8, 5 }, 
                                      { 0, 3, 0, 0, 7 }, 
                                      { 6, 8, 0, 0, 9 }, 
                                      { 0, 5, 7, 9, 0 } }; 
  
        // Print the solution 
        primMST(graph); 
    } 
} 
  
// This code is contributed by anuj_67. 

پیچیدگی زمانی روش مورد استفاده در کدهای بالا، از درجه (O(V² است. اگر گراف ورودی با استفاده از لیست مجاورت نمایش داده شود، پیچیدگی زمانی الگوریتم پریم را می‌توان به کمک «هرم دودویی» (Binary Heap) به درجه (O(E log V کاهش داد.

فیلم مجموعه آموزش ساختمان داده و طراحی الگوریتم در فرادرس

کلیک کنید

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش برنامه‌نویسی C++‎
• مجموعه آموزش‌های ریاضیات
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• برنامه تشخیص وجود دور در گراف جهت‌دار — راهنمای کاربردی
• برنامه بررسی وجود دور در گراف بدون جهت — راهنمای کاربردی

^^