تجزیه اعداد – به زبان ساده

در ادامه مجموعه آموزش‌های ریاضی مجله فرادرس، در این آموزش درباره تجزیه اعداد به عوامل اول بحث خواهیم کرد. فرهنگستان زبان و ادبیات فارسی، برای دو واژه انگلیسی Factor و Factorization در ریاضی، به‌ترتیب، معادل‌های «عامل» و «عامل‌یابی» را برگزیده است.

در ریاضیات، «عامل» به‌معنی یک عدد یا چندجمله‌ای است که عدد یا چندجمله‌ای مفروضی بر آن بخش‌پذیر است. همچنین، «عامل‌یابی» یا «تجزیه به عامل‌ها» نیز، نوشتن یک عدد یا چندجمله‌ای به‌صورت حاصل‌ضرب چند عدد یا چندجمله‌ای است.

اعداد اول

همان‌طور که در آموزش‌های قبلی مجله فرادرس گفتیم، عدد اول عددی است که فقط بر ۱ و خودش بخش‌پذیر است و باید عددی بزرگتر از ۱ باشد. اعداد ۲، ۳، ۵، ۷، ۱۱، 13 و... اعداد اول هستند.

عامل‌ها

عامل‌ها یا شمارنده‌ها یا مقسوم‌علیه‌ها، اعدادی هستند که در هم ضرب می‌شوند و یک عدد دیگر را می‌سازند. به‌عبارت دیگر، عامل‌های یک عدد، مقسوم‌علیه‌های آن عدد (با باقیمانده صفر) هستند. برای مثال، ۲ و ۳ در هم ضرب شده و عدد ۶ را می‌سازند. بنابراین، اعداد ۲ و ۳، عامل‌های عدد ۶ هستند.

تجزیه به اعداد اول

عامل‌های یک عدد، لزوماً اعداد اول نیستند. برای مثال، عدد ۱۲ را می‌توان به‌صورت حاصل‌ضرب دو عدد ۶ و ۲ نوشت که ۶ عدد اول نیست، ولی عاملی برای عدد ۱۲ است. عامل‌های اول یک عدد در موارد زیادی مورد استفاده قرار می‌گیرد و معمولاً اعداد را به عامل‌های اول تجزیه می‌کنند. تجزیه یک عدد به عامل‌های اول، یافتن اعداد اولی است که با ضرب آن‌ها در یکدیگر، آن عدد ساخته می‌شود. در ادامه، چند مثال را بررسی می‌کنیم.

مثال ۱

عامل‌های اول عدد ۱۲ چه اعدادی هستند؟

حل: برای یافتن عامل‌های اول یک عدد، آن عدد را بر اعداد اول تقسیم می‌کنیم و بهترین کار، شروع از کوچکترین عدد اول، یعنی ۲ است. بنابراین:

$$\large 12 \div 2 = 6$$

همان‌طور که می‌بینیم، 12 بر 2 بخش‌پذیر است. اما 6 یک عدد اول نیست و باید ادامه دهیم. این بار هم از کوچکترین عدد اول، یعنی 2 شروع می‌کنیم:

$$\large 6 \div 2 = 3$$

حاصل برابر با 3 است که خود عددی اول بوده و دیگر بخش‌پذیر نیست. بنابراین، عدد 12 را می‌توان به‌صورت زیر به عوامل اول تجزیه کرد:

$$\large 12 = 2 \times 2 \times 3$$

همان‌گونه که می‌بینیم، هر عامل، یک عدد اول بوده و در نتیجه، پاسخ صحیح است.

مثال ۲

عدد 147 را به عوامل اول تجزیه کنید.

حل: ابتدا از عدد 2 شروع می‌کنیم:

$$\large 147 \div 2 = 73.5$$

همان‌گونه که می‌بینیم، عدد 147 بر  2 بخش‌پذیر نیست. عدد بعدی، یعنی $$3$$ را بررسی می‌کنیم:

$$\large 147 \div 3 = 49$$

می‌بینیم که عدد 147 بر 3 بخش‌پذیر است. حال عوامل عدد 4۹ را پیدا می‌کنیم. می‌دانیم کوچکترین عدد اولی که 49 بر آن بخش‌پذیر است، عدد 7 است.

$$\large 49 \div 7 = 7$$

بنابراین، عدد 147 را می‌توان به‌صورت ضرب عوامل اول زیر نوشت:

$$\large 147 = 3 \times 7 \times 7$$

مثال ۳

عوامل اول عدد 17 را بیابید.

حل: عدد 17 بر عوامل اول 2، 3، 5، 7، 11 و 13 بخش‌پذیر نیست و خودش یک عدد اول است. بنابراین:

$$\large 17 = 17$$

یک روش دیگر برای تجزیه اعداد

دیدیم که برای محاسبه عوامل اول، باید عدد مورد نظر را بر کوچکترین عدد اول تقسیم کرده و به‌ همین ترتیب ادامه دهیم. اما گاهی اوقات، شکستن عدد به هر عاملی (غیر از اعداد اول) که ممکن است و تجزیه آن عوامل به عوامل اول، کار ساده‌تری است.

فیلم آموزش ریاضی پایه هفتم – جامع و با نکات مهم در فرادرس

کلیک کنید

برای مثال فرض کنید می‌خواهیم عدد 90 را به عوامل اول تجزیه کنیم. برای این کار، ساده‌تر است که این عدد را به‌صورت $$9 \times 10$$ بشکنیم و عوامل اول اعداد $$9$$ و $$10$$ را بنویسیم:

• عوامل اول 9، اعداد 3 و3 هستند.
• عوامل اول 10، اعداد 2 و 5 هستند.

بنابراین، عوامل اول عدد 90، اعداد 3، 3، 2 و 5 هستند.

تجزیه درختی

تجزیه درختی اعداد به عوامل اول، روشی مشابه روش اخیر است که در آن، ابتدا عدد را به هر عاملی (غیر از اعداد اول) تجزیه کرده و سپس این عوامل را به عوامل اول تجزیه می‌کنیم.

برای مثال، وقتی عدد 48 را می‌بینیم، حاصل‌ضرب $$6 \times 8$$ را به‌خاطر می‌آوریم. بنابراین، می‌توان عدد 48 را به‌صورت ضرب عوامل 6 و 8 نوشت:

$$\large 48 = 8 \times 6$$

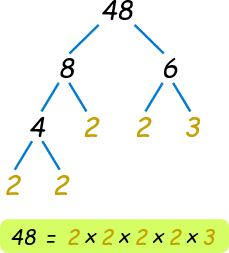
اکنون عامل 8 را به‌صورت $$4 \times 2$$ می‌نویسیم. سپس 4 به‌شکل ضرب عوامل اول $$2 \times 2$$ نوشته می‌شود. در نهایت، عدد 6 به‌صورت $$3 \times 2$$ تجزیه می‌شود.

همان‌گونه که می‌بینیم نمی‌توان بیش از این ادامه داد و عدد را به عوامل اول دیگر تجزیه کرد. بنابراین، عدد $$48$$ را می‌توان به‌صورت زیر نوشت:

$$\large 2 \times 2 \times 2 \times 2 \times 3$$

یا    $$48 = 2^ 4 \times 3$$

شکل درختی زیر، این عملیات را نشان می‌دهد:

چرا عوامل اول اعداد را پیدا می‌کنیم؟

همان‌طور که قبلاً گفتیم، یک عدد اول، فقط بر 1 و خودش بخش‌پذیر است. بنابراین، نمی‌توان آن را تجزیه کرد. اما سایر اعداد را می‌توان به اعداد اول تجزیه کرد. اعداد اول، مانند بلوک‌های اصلی ساختمان همه اعداد هستند. از این ایده می‌توان در بسیاری از موارد مانند رمزنگاری استفاده کرد.

رمزنگاری، علم مطالعه رمزهای مخفی است. تجزیه به اعداد اول، برای افرادی که کدها را براساس اعداد می‌نویسند یا می‌شکنند، اهمیت فراوانی دارد. دلیل این اهمیت این است که تجزیه و تحلیل اعداد بسیار بزرگ، بسیار دشوار است و زمان زیادی از کامپیوترها می‌گیرد.

یکتایی عامل‌های اول

در تجزیه اعداد به عوامل اول، باید به این نکته دقت کرد که فقط یک مجموعه یکتا و منحصربه‌فرد از اعداد اول وجود دارد که عوامل یک عدد هستند و می‌توان آن عدد را به آن‌ها تجزیه کرد. برای مثال، عوامل اول عدد 330، اعداد 2، 3، 5 و 11 هستند:

$$\large 330 = 2 \times 3 \times 5 \times 11$$

و هیچ ترکیب دیگری از مجموعه اعداد اول وجود ندارد که بتوان آن‌ها را در هم ضرب کرد و به عدد 330 رسید.