حل مساله n وزیر با الگوریتم پس گرد (Backtracking) – به زبان ساده

شایان توجه است که در مساله n وزیر، برای n=2 و n=۳ پاسخی وجود ندارد. همچنین، الزاما تعداد راهکارهای موجود برای مساله با افزایش N افزایش پیدا نمی‌کنند. برای مثال، مساله ۶ وزیر، تعداد پاسخ‌های کمتری نسبت به حالت ۵ وزیر دارد. در ادامه، روش حل مساله n وزیر برای N=4 نمایش داده شده است؛ سپس، یک الگوریتم ساده برای حل آن معرفی و در نهایت، مساله ۴ وزیر با استفاده از «الگوریتم پَس‌گرد» (Backtracking Algorithm) حل شده است. پیاده‌سازی الگوریتم پس‌گرد برای حل مساله N وزیر با زبان‌های برنامه‌نویسی C++/C، پایتون و جاوا انجام شده است.

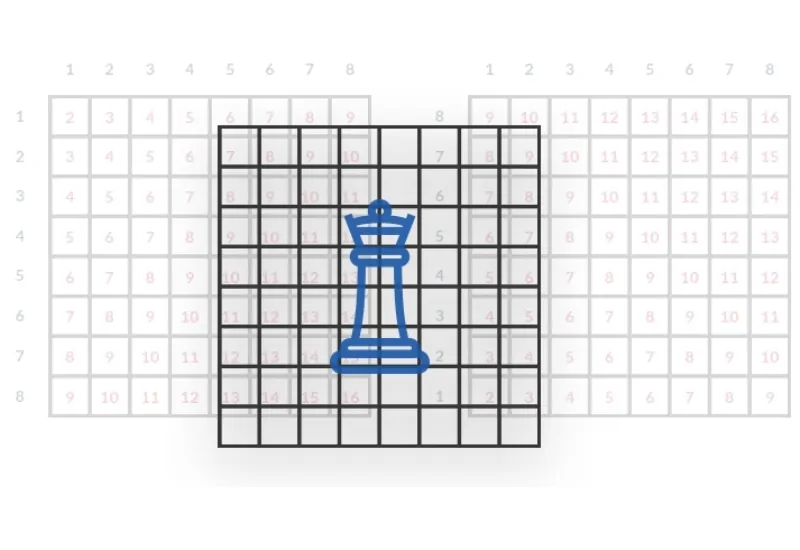
خروجی مورد انتظار، یک ماتریس دودویی است که در آن ۱ برای محل‌هایی که وزیر در آن قرار گرفته و ۰ برای محل‌های فاقد وزیر است. برای مثال، ماتریس خروجی زیر، برای مساله ۴ وزیر است که تصویر آن در بالا وجود دارد.

 { 0, 1, 0, 0}
{ 0, 0, 0, 1}
{ 1, 0, 0, 0}
{ 0, 0, 1, 0}

الگوریتم ساده برای حل مساله N وزیر

الگوریتم ساده برای حل مساله n وزیر، همه پیکربندی‌های ممکن برای وزیرها روی صفحه را تولید می‌کند و پیکربندی را چاپ می‌کند که محدودیت‌های داده شده را ارضا می‌کند.

while there are untried configurations { generate the next configuration if queens don't attack in this configuration then { print this configuration; } }

 الگوریتم پَس‌گرد

در الگوریتم «پَس‌گرد» (Backtracking)، ایده آن است که وزیرها یکی یکی در ستون‌های متفاوت قرار بگیرند و کار از چپ‌ترین ستون آغاز می‌شود. هنگامی که یک وزیر در ستون قرار می‌گیرد، بررسی می‌شود که آیا وزیر جدید قرار داده شده با سایر وزیرهای قرار گرفته در صفحه تصادم دارد یا خیر.

فیلم آموزش حل مسئله n وزیر با الگوریتم عقبگرد در فرادرس

کلیک کنید

در ستون کنونی، اگر سطری پیدا شود که هیچ ضربی بین وزیر جدید و سایر وزیرها وجود نداشته باشد، وزیر در آنجا قرار داده می‌شود. در غیر این صورت، پس‌گرد اتفاق می‌افتد و false بازگردانده می‌شود. الگوریتم پَس‌گرد برای حل مساله n وزیر، به صورت زیر است:

1. از چپ‌ترین ستون شروع کن.
2. اگر همه وزیرها قرار گرفته‌اند،
   • True را بازگردان
3. همه سطرها در ستون کنونی را بررسی کن. اقدامات زیر را برای هر سطر آزموده شده انجام بده.
   • اگر وزیر بتواند به صورت امن در این سطر قرار بگیرد، آن را [row, column] به عنوان بخشی از راهکار علامت‌گذاری کن و به طور بازگشتی بررسی کن که آیا قرار دادن وزیر در اینجا منجر به راهکار می‌شود.
   • اگر قرار دادن وزیر در [row, column] منجر به راهکار می‌شود، true را بازگردان.
   • اگر قرار دادن وزیر منجر به یک راهکار شود، نشانه‌گذاری آن را بردار [row, column] (پس‌گرد) و به مرحله a برو و سطر دیگری را بررسی کن.
4. اگر همه سطرها مورد بررسی قرار گرفتند و هیچ یک پاسخ نبودند، false را به trigger backtracking (عامل عقب‌نشینی) بازگردان.

پیاده‌سازی مساله N وزیر در ++C/C

پیاده سازی مساله N وزیر در پایتون

پیاده سازی مساله N وزیر در جاوا

خروجی؛ مقدار ۱ نشان‌گر محل قرارگیری وزیر است.

 0 0 1 0 
1 0 0 0 
0 0 0 1 
0 1 0 0

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• معرفی منابع آموزش ویدئویی هوش مصنوعی به زبان فارسی و انگلیسی
• زبان برنامه‌نویسی پایتون (Python) — از صفر تا صد
• آموزش ساختمان داده — مجموعه مقالات جامع وبلاگ فرادرس
• پشته در ساختمان داده چیست؟ – به زبان ساده

^^