فرادرس
شبیه سازی تبرید (Simulated Annealing) – به زبان ساده
در ریاضیات و علوم کامپیوتر، «مساله بهینه‌سازی» (Optimization Problem)، در واقع مساله پیدا کردن «بهترین» راه حل، از میان کلیه راه حل‌های «ممکن» برای مساله است. نوع خاصی از مسائل بهینه‌سازی وجود دارند که در آن‌ها، به دلیل زیاد شدن تعداد «اشیا» (Objects) (منظور تعداد مشاهدات است)، مدیریت کردن آن‌ها با استفاده از «روش‌های ترکیبیاتی» (Combinatorial Methods) امکان‌پذیر نیست. یک مثال شناخته شده از چنین مسائلی، «مساله فروشنده دوره‌گرد» (Traveling Salesman Problem) است که از دسته مسائل «ان‌پی کامل» (NP-Complete که در آن، NP سرنامی برای عبارت Non-Deterministic Polynomial است) محسوب می‌شود.
برای حل چنین مسائلی، یک الگوریتم بسیار کاربردی به نام «شبیه سازی تبرید» (Simulated Annealing) (به آن «تبرید شبیه سازی شده»، «بازپخت شبیه سازی شده» و یا به طور خلاصه، SA نیز گفته می‌شود) وجود دارد. از الگوریتم شبیه سازی تبرید اغلب برای تخمین «بهینه سراسری» (Global Optimization) در مسائل بهینه‌سازی که فضای جستجوی آن‌ها بزرگ است، استفاده می‌شود.
همچنین، این الگوریتم معمولا هنگامی که فضای جستجو گسسته باشد، مورد استفاده قرار می‌گیرد (همه سفرهایی که از مجموعه مشخصی از شهرها طی آن‌ها عبور می‌شود). در این مطلب، به الگوریتم شبیه سازی تبرید و کاربرد آن در حل مسائل بهینه‌سازی پرداخته می‌شود، اما پیش از پرداختن به الگوریتم، مفهوم فرایند بازپخت (انیلینگ | Annealing) در «متالورژی» (Metallurgy) که الگوریتم تبرید شبیه سازی شده در واقع تقلیدی از آن است، بیان خواهد شد. سپس، الگوریتم شبیه سازی تبرید شرح داده می‌شود و در نهایت به حل مساله فروشنده دوره‌گرد با آن پرداخته می‌شود. کد مربوط به پیاده‌سازی الگوریتم شبیه سازی تبرید در زبان برنامه‌نویسی «پایتون» (Python) و «جاوا» (Java) در انتخای این مطلب، ارائه شده است.
فرایند بازپخت یا انیلینگ
در متالورژی و علم مواد، بازپخت یا انیلینگ، به عملیات حرارتی گفته می‌شود که طی آن مشخصات فیزیکی و گاهی، مشخصات شیمیایی ماده تغییر می‌کند. این کار با هدف افزایش شکل‌پذیری و کاهش سختی ماده انجام می‌شود. طی این فرایند، ابتدا فلز گرم شده، سپس در یک درجه حرارت خاص نگه داشته و در نهایت، به تدریج سرد می‌شود.
با گرم کردن فلز، مولکول‌ها آزادانه به هر سوی حرکت می‌کنند. با سرد کردن تدریجی ماده، این آزادی کاهش پیدا می‌کند. اگر فرایند سرد کردن به اندازه کافی کند باشد که بتوان اطمینان حاصل کرد فلز در هر مرحله در تعادل ترمودینامیکی قرار دارد، می‌توان مطمئن شد که انرژی گرمایی به طور یکنواخت در جسم توزیع شده و بهترین ساختار بلوری در آن وجود دارد که متقارن و مقاوم است. در الگوریتم شبیه‌سازی تبرید، از فرایند مذکور الگوبرداری شده است.
مساله فروشنده دوره‌گرد
در مساله «فروشنده دوره‌گرد» (Travelling Salesman Problem | TSP)، پرسش زیر مطرح می‌شود:
لیستی از شهرها و فاصله بین هر جفت از شهرها موجود است. کوتاه‌ترین مسیر ممکنی که با استفاده از آن بتوان از یک نقطه شروع کرد و پس از عبور از همه شهرها به نقطه اول بازگشت، کدام است؟
این مساله، یکی از مسائل «ان‌پی-سخت» (NP-Hard) در بهینه‌سازی کامپیوتری محسوب می‌شود که در حوزه «تحقیق در عملیات» (Operational Research | OR) و «علوم نظری رایانه» (Theoretical Computer Science | TCS) حائز اهمیت است. در «نظریه پیچیدگی محاسباتی» (Theory of Computational Complexity)، نسخه تصمیم مساله فروشنده دوره‌گرد (که در آن یک طول L داده شده، وظیفه تصمیم‌گیری پیرامون آن است که آیا گراف دارای دوری کمتر از L است یا خیر) از جمله مسائل ان‌پی-کامل محسوب می‌شود.
بنابراین، این امکان وجود دارد که بدترین زمان اجرا برای هر الگوریتم برای TSP، با افزایش تعداد شهرها به صورت «فوق چند جمله‌ای» (Superpolynomially) افزایش پیدا کند (اما نه بیشتر از نمایی).
این مساله برای اولین بار در سال ۱۹۳۰ فرموله شد و یکی از مسائلی است که بیشترین مطالعات در حوزه بهینه‌سازی روی آن انجام شده است. از این مساله، به عنوان «بنچ‌مارک» (Benchmark) برای بسیاری از روش‌های بهینه‌سازی استفاده می‌شود. هرچند حل مساله فروشنده دوره‌گرد حتی به لحاظ کامپیوتری نیز دشوار است، تعداد زیادی از «روش‌های تکاملی» (Evolutionary Algorithms) و «الگوریتم‌های دقیق» (Exact Algorithm) برای حل این مساله شناخته شده هستند که می‌توانند TSP را با تعداد هزاران و حتی میلیون‌ها شهر حل کنند. مساله فروشنده دوره‌گرد را می‌توان به صورت یک مساله گراف و یا «برنامه‌نویسی خطی صحیح» (Integer Linear Programming) فرموله کرد. تعداد کل پاسخ‌های ممکن برای مساله برابر با «$$\frac{1}{2}\left(n-1\right)!$$» برای n>2 است که در آن، n تعداد کل شهرها است. در واقع، این عدد تعداد دورهای همیلتونی در یک گراف کامل با n راس را نشان می‌دهد.
الگوریتم شبیه سازی تبرید
همانطور که پیش‌تر بیان شد، در الگوریتم شبیه سازی تبرید (یا تبرید شبیه سازی شده) از فرایند بازپخت که از مباحث رشته متالورژی و مواد محسوب می‌شود، الگو گرفته شده است. انتخاب نام شبیه‌سازی تبرید برای این الگوریتم، ریشه در فرایند دارد که از آن تقلید می‌کند. در بهینه‌سازی نیز مانند فرایند انیلینگ، آنچه در بخش پیشین پیرامون بازپخت مواد بیان شد، برای حل مسائل قابل انجام است.
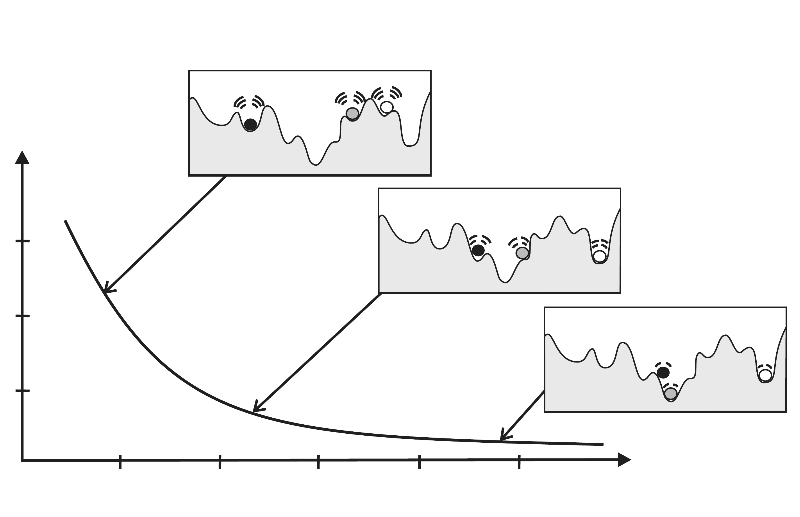
یعنی در واقع، جواب‌های یک مساله به خوبی گرم می‌شوند و با نوسانات زیادی تغییر می‌کنند؛ سپس، به تدریج دامنه تغییرات کم می‌شود و در واقع یک سری شیار به سمت جواب بهینه ساخته می‌شوند. الگوریتم شبیه سازی تبرید برای اولین بار در سال ۱۹۸۳، توسط «کریک‌پاتریک» (Kirkpatrick) و همکاران معرفی شد. شایان ذکر است، الگوریتم شبیه سازی تبرید از جمله الگوریتم‌های فراابتکاری (فراتکاملی | فرااکتشافی | Metaheuristic) محسوب می‌شود. در الگوریتم شبیه سازی تبرید، از روش احتمالاتی برای حل مساله بهینه‌سازی استفاده می‌شود. علاقمندان به مشاهده ویدئوی آموزشی این الگوریتم به زبان فارسی، می‌توانند از «آموزش شبیه‌سازی تبرید یا Simulated Annealing در متلب» بهره‌مند شوند.
در الگوریتم شبیه سازی تبرید (SA)، نقطه s یک حالت از سیستم فیزیکی محسوب می‌شود و تابع (E(s مشابه با انرژی داخلی سیستم در حالت s است. هدف آن است که با شروع سیستم از یک حالت اولیه دلخواه (یک s0 دلخواه)، به حالتی رسیده شود (Sn) که تابع (E(s در آن کمینه است. در واقع، با شروع از یک حالت دلخواه از سیستم فیزیکی، به حالتی رسیده می‌شود که انرژی داخلی سیستم در آن حالت کمینه است (سیستم کمترین انرژی را در آن حالت خواهد داشت). برای انجام این کار، الگوریتم از یک نقطه دلخواه آغاز به کار و سپس، یک حالت همسایه را انتخاب می‌کند. پس از آن، به طور احتمالی تصمیم می‌گیرد که در حالت کنونی بماند و یا به حالت همسایه جا به جا شود. مجموع این جا به جایی‌های احتمالی، سیستم را به سوی حالتی با انرژی داخلی کمتر هدایت می‌کند. این کار تا جایی انجام می‌شود که سیستم به یک حالت عقلانی برسد یا اینکه میزان محاسبات، از یک آستانه مشخص بیشتر شود. برای درک بهتر وجه تمایز الگوریتم شبیه سازی تبرید با برخی از دیگر روش‌های ابتکاری مانند تپه‌نوری، مثال زیر قابل توجه است.
مساله فروشنده دوره‌گرد را می‌توان به عنوان مثالی در نظر گرفت که الگوریتم شبیه سازی تبرید در حل آن کاربرد دارد. همانطور که پیش‌تر بیان شد، در این مساله، فروشنده باید از تعداد زیادی از شهرها در حالی عبور کند که مسافت کل پیموده شده کمینه باشد. اگر فروشنده از یک مسیر تصادفی حرکت خود را آغاز کند، بعدا می‌تواند با این امید که در هر تغییر شهر مسافت پیموده شده را کاهش دهد، به ترتیب از کلیه شهرها عبور کند.
چالش اصلی در حل مساله فروشنده دوره گرد با استفاده از روشی مانند الگوریتم «تپه‌نوردی» (Hill Climbing)، از آنجا نشات می‌گیرد که این الگوریتم با جا به جایی بین همسایه‌ها معمولا به حالت کمینه می‌رسد و در همان نقطه متوقف می‌شود (در واقع در حالتی که نسبت به دیگر همسایگی‌های بررسی شده کمینه باشد متوقف می‌شود؛ در صورتی که امکان دارد یک کمینه سراسری وجود داشته باشد). در واقع، الگوریتم تپه‌نوردی «کمینه محلی» (Local Minimum) را معمولا به سرعت پیدا می‌کند، اما ممکن است در همان جا متوقف شود و بنابراین از آنجا به «کمینه سراسری» (Global Minimum) نمی‌رسد. این در حالی است که شبیه‌سازی تبرید می‌تواند راه حل خیلی خوبی را حتی در حضور «نویز» (Noise) برای چنین مساله‌ای پیدا کند.
راهکار الگوریتم شبیه سازی تبرید برای غلبه بر این مشکل و بهبود استراتژی مذکور، استفاده از دو ترفند است. ترفند اول، از «الگوریتم متروپولیس» (Metropolis Algorithm) گرفته شده که در سال ۱۹۵۳ توسط متروپولیس و همکاران اون کشف شده است. در این الگوریتم، گاهی مسیرهای کوتاه پذیرفته نمی‌شوند، زیرا این عدم پذیرش منجر به آن می‌شود که الگوریتم «فضای راه حل ممکن» بزرگ‌تری را اکتشاف کند. ترفند دوم، مجددا با تقلید از فرایند بازپخت فلز و کاهش دما به دمای پایین‌تر اتفاق می‌افتد. پس از آنکه بررسی‌ها و جا به جایی‌های زیادی انجام شد و مشاهده شد که تابع (E(s (این تابع در واقع همان تابع هزینه یا Cost Function است) به آرامی کاهش پیدا می‌کند (دما کاهش پیدا می‌کند)، اندازه انجام جا به جایی‌های «بد» کنترل می‌شود. پس از چندین بار کاهش دما به مقدار کمتر، فرایند «فرونشانی» (Quench) با پذیرش جا به جایی‌های خوب به منظور پیدا کردن کمینه محلی تابع هزینه اتفاق می‌افتد. «زمان‌بندی‌های بازپخت» (Annealing Schedules) متعددی برای کاهش درجه حرارت وجود دارد، اما نتایج به طور کلی خیلی به جزئیات حساس نیستند.
اکنون، الگوریتم شبیه سازی تبرید به صورت ریاضیاتی و دقیق ارائه می‌شود. احتمال انتقال از یک حالت فعلی، مثلا s به حالت کاندید جدید مانند $$s\prime$$ با یک تابع احتمال پذیرش $$P(e,e\prime,T)$$ مشخص می‌شود که در آن، (e=E(s و $$e\prime=E(s\prime)$$ است (چنانچه پیش‌تر بیان شد، تابع E در فضای حالت نشان‌گر انرژی داخلی سیستم و T نشان‌گر دما است. دمای T بر اساس زمان تغییر می‌کند). بنابراین، با توجه به آنکه پیش‌تر گفته شد هدف آن است که انرژی سیستم کمینه باشد، پس حالتی که (منظور s است) در آن (E(s کمتر باشد، بهتر از حالتی است که در آن مقدار (E(s بیشتر باشد. نکته قابل توجه در الگوریتم تبرید شبیه سازی شده آن است که تابع احتمال P همواره و حتی در شرایطی که e کوچک‌تر از $$e\prime$$ است، باید مثبت باشد. این خصوصیت موجب می‌شود الگوریتم در بهینه محلی که نسبت به بهینه سراسری «بدتر» است، متوقف نشود. در واقع، در صورتی که $$s\prime$$ بهتر از s $$E(s)\ge E(s\prime)$$ باشد، $$s\prime$$ پذیرفته می‌شود و اگر $$s\prime$$ بدتر از s باشد و موجب $$E(s)< E(s\prime)$$ شود، $$s\prime$$ با یک احتمال پذیرفته می‌شود. تابع احتمال P به صورت زیر است:
$$p=e^{-\frac{E(s\prime)-E(s)}{T}}=e^{-\frac{\Delta f}{T}}$$
در صورت کاهش دمای T و میل کردن آن به سمت صفر، احتمال P نیز باید کاهش پیدا کند و یا به صفر و یا یک عدد مثبت میل کند. در این شرایط، P هنگامی به سمت صفر میل می‌کند که $$e<e\prime$$ باشد و در صورتی به یک عدد مثبت میل می‌کند که $$e\prime<e$$ باشد. همانطور که مشهود است، دما در کنترل تغییرات سیستم نقش اساسی دارد. همانطور که پیش‌تر هم بیان شد، دما در شبیه‌سازی به صورت تدریجی کاهش پیدا می‌کند. بنابراین، الگوریتم از $$T=\infty$$ و به عبارتی، از یک دمای بسیار بزرگ کار خود را آغاز می‌کند و در هر مرحله با توجه به یک زمان‌بندی تبرید از پیش مشخص شده، کاهش پیدا می‌کند. زمان‌بندی تبرید با توجه به این موضوع انجام می‌شود که اگر منابع مورد استفاده (مثلا میزان محاسبات) به پایان برسند، زمان انجام فرایند نیز به پایان می‌رسد. از همین رو، الگوریتم ابتدا در فضای بزرگی از راه حل‌ها، صرف نظر از انرژی داخلی سیستم به دنبال پاسخ می‌گردد و به تدریج، به سمت مناطق دارای انرژی کمتر جا به جا می‌شود. این منطقه، به تدریج کوچک‌تر می‌شود و این کار، تا زمانی که بهینه سراسری یافته شود، ادامه پیدا می‌کند. برای یک مساله دارای فضای متناهی، افزایش زمان موجب می‌شود تا با احتمال یک، الگوریتم در نقطه بهینه سراسری متوقف شود؛ هر چند زمان لازم برای انجام این کار، بیشتر از زمان لازم برای جستجو در کل فضا است و بنابراین، این موضوع در عمل کاربردی ندارد.
فلوچارت الگوریتم شبیه سازی تبرید
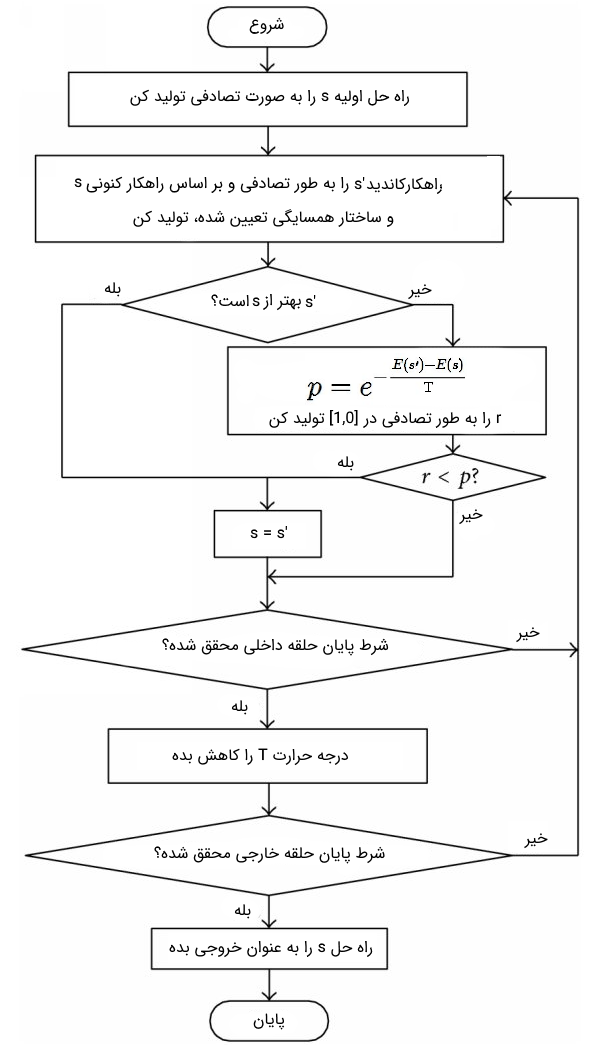
حل مساله فروشنده دوره‌گرد با شبیه سازی تبرید
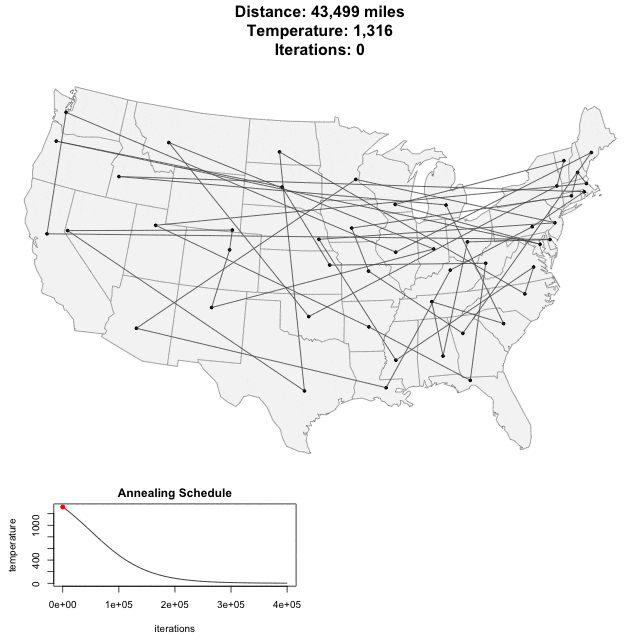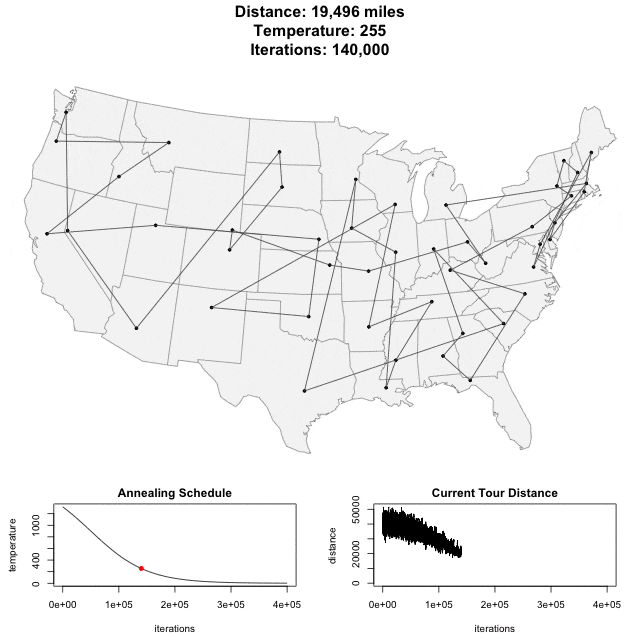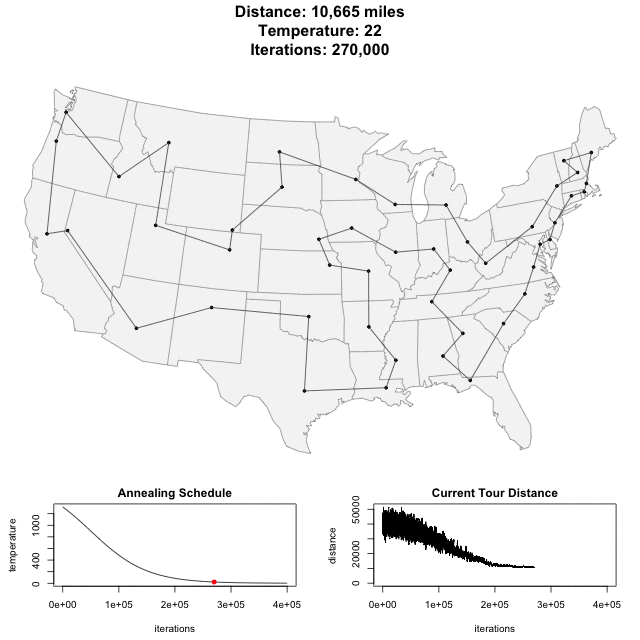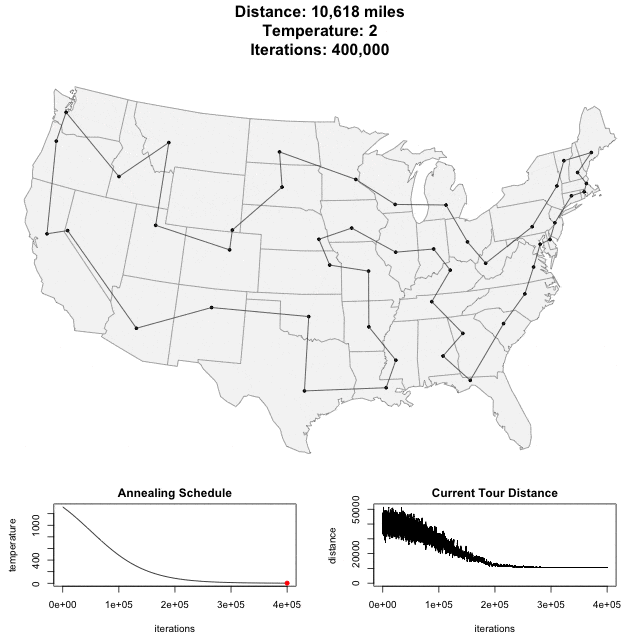
برنامه‌ای که با بهره‌گیری از آن می‌توان مساله فروشنده دوره‌گرد را با الگوریتم شبیه سازی تبرید حل کرد، از این مسیر [+] در دسترس است. در ادامه، انیمیشن مربوط به حل مساله فروشنده دوره‌گرد با استفاده از این برنامه برای ۴۸ تا از مراکز استان‌های ایالات متحده آمریکا، قابل مشاهده است.
شبه کد الگوریتم تبرید شبیه سازی شده
Let s = s0 For k = 0 through kmax (exclusive): T ← temperature( kmax/(k+1) ) Pick a random neighbour, snew ← neighbour(s) If P(E(s), E(snew), T) ≥ random(0, 1): s ← snew Output: the final state s
کد الگوریتم تبرید شبیه سازی شده در جاوا
// Java program to implement Simulated Annealing
import java.util.*;
public class SimulatedAnnealing {
// Initial and final temperature
public static double T = 1;
// Simulated Annealing parameters
// Temperature at which iteration terminates
static final double Tmin = .0001;
// Decrease in temperature
static final double alpha = 0.9;
// Number of iterations of annealing
// before decreasing temperature
static final int numIterations = 100;
// Locational parameters
// Target array is discretized as M*N grid
static final int M = 5, N = 5;
// Number of objects desired
static final int k = 5;
public static void main(String[] args) {
// Problem: place k objects in an MxN target
// plane yielding minimal cost according to
// defined objective function
// Set of all possible candidate locations
String[][] sourceArray = new String[M][N];
// Global minimum
Solution min = new Solution(Double.MAX_VALUE, null);
// Generates random initial candidate solution
// before annealing process
Solution currentSol = genRandSol();
// Continues annealing until reaching minimum
// temprature
while (T > Tmin) {
for (int i=0;i<numIterations;i++){
// Reassigns global minimum accordingly
if (currentSol.CVRMSE < min.CVRMSE){
min = currentSol;
}
Solution newSol = neighbor(currentSol);
double ap = Math.pow(Math.E,
(currentSol.CVRMSE - newSol.CVRMSE)/T);
if (ap > Math.random())
currentSol = newSol;
}
T *= alpha; // Decreases T, cooling phase
}
//Returns minimum value based on optimiation
System.out.println(min.CVRMSE+"\n\n");
for(String[] row:sourceArray) Arrays.fill(row, "X");
// Displays
for (int object:min.config) {
int[] coord = indexToPoints(object);
sourceArray[coord[0]][coord[1]] = "-";
}
// Displays optimal location
for (String[] row:sourceArray)
System.out.println(Arrays.toString(row));
}
// Given current configuration, returns "neighboring"
// configuration (i.e. very similar)
// integer of k points each in range [0, n)
/* Different neighbor selection strategies:
* Move all points 0 or 1 units in a random direction
* Shift input elements randomly
* Swap random elements in input sequence
* Permute input sequence
* Partition input sequence into a random number
of segments and permute segments */
public static Solution neighbor(Solution currentSol){
// Slight perturbation to the current solution
// to avoid getting stuck in local minimas
// Returning for the sake of compilation
return currentSol;
}
// Generates random solution via modified Fisher-Yates
// shuffle for first k elements
// Pseudorandomly selects k integers from the interval
// [0, n-1]
public static Solution genRandSol(){
// Instantiating for the sake of compilation
int[] a = {1, 2, 3, 4, 5};
// Returning for the sake of compilation
return new Solution(-1, a);
}
// Complexity is O(M*N*k), asymptotically tight
public static double cost(int[] inputConfiguration){
// Given specific configuration, return object
// solution with assigned cost
return -1; //Returning for the sake of compilation
}
// Mapping from [0, M*N] --> [0,M]x[0,N]
public static int[] indexToPoints(int index){
int[] points = {index%M, index/M};
return points;
}
// Class solution, bundling configuration with error
static class Solution {
// function value of instance of solution;
// using coefficient of variance root mean
// squared error
public double CVRMSE;
public int[] config; // Configuration array
public Solution(double CVRMSE, int[] configuration) {
this.CVRMSE = CVRMSE;
config = configuration;
}
}
}
کد الگوریتم تبرید شبیه سازی شده در پایتون
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
Module for implementing Simulated Annealing algorithm for single objective optimization.
author := "Daniel Barker"
"""
import random
import math
import numpy as np
import pandas as pd
import plotly.plotly as py
import plotly.graph_objs as go
# Formatting variables
HEADER = '++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++'
SPACER = '===================================================================='
FOOTER = '********************************************************************'
class SimulatedAnnealing(object):
""" Class for performing SimulatedAnnealing optimization algorithm."""
def __init__(self, start_temp, stop_temp, alpha, num_sims):
"""
Constructor Method.
"""
self.start_temp = start_temp
self.stop_temp = stop_temp
self.alpha = alpha
self.num_sims = num_sims
def _random_int(self, lower_bound, upper_bound, step):
return random.randrange(lower_bound, upper_bound, step)
def _random_float(self, lower_bound, upper_bound, sig_dig):
return round(random.uniform(lower_bound, upper_bound), sig_dig)
def _get_neighbor_int(self, current_value, distance, step, lower_bound, upper_bound):
""" Return a neighboring random integer value from some current value.
:param distance: defines neighborhood as current value +- distance
:param step: step size range within neighborhood
:param lower_bound: hard cutoff lower bound that overrides distances lower than this threshold
:param upper_bound: hard cutoff upper bound that overrides distances higher than this threshold
:return: random value within neighborhood of current input value
"""
upper_neighbor = current_value + distance
if upper_neighbor > upper_bound:
upper_neighbor = upper_bound
else:
upper_neighbor = upper_neighbor
lower_neighbor = current_value - distance
if lower_neighbor < lower_bound:
lower_neighbor = lower_bound
else:
lower_neighbor = lower_neighbor
neighbor = random.randrange(lower_neighbor, upper_neighbor, step)
return neighbor
def _get_neighbor_float(self, current_value, distance, lower_bound, upper_bound, sig_dig):
""" Return a neighboring random float from some current value.
:param distance: defines neighborhood as current value +- distance
:param sig_dig: number of significant digits in result
:param lower_bound: hard cutoff lower bound that overrides distances lower than this threshold
:param upper_bound: hard cutoff upper bound that overrides distances higher than this threshold
:return: random value within neighborhood of current input value
"""
upper_neighbor = current_value + distance
if upper_neighbor > upper_bound:
upper_neighbor = upper_bound
else:
upper_neighbor = upper_neighbor
lower_neighbor = current_value - distance
if lower_neighbor < lower_bound:
lower_neighbor = lower_bound
else:
lower_neighbor = lower_neighbor
neighbor = random.uniform(lower_neighbor, upper_neighbor)
neighbor = round(neighbor, sig_dig)
return neighbor
def _roll_dice(self, delta, t_new):
"""
Method to calculate the probability of acceptance
:param delta: difference between the new cost and the old cost
:param t_new: the current temperature of the annealing algorithm
:return: Accept the new design? (True/False)
"""
pa = math.exp(delta / t_new)
print('Probability of Acceptance = ' + str(pa) + ' %')
r = random.random()
print('Rolling the dice... = ' + str(r) + '%')
decision = pa - r
if decision >= 0:
d = True
else:
d = False
return d
def run_annealing(self, xy_function, x_ub, x_lb, y_ub, y_lb, x_neighbor_distance, y_neighbor_distance):
""" Run the annealing algorithm.
INPUTS:
xy_function :: (function) 2-D function of x and y
x_ub :: (float) Upper X-boundary of search space
x_lb :: (float) Lower X-boundary of search space
y_ub :: (float) Upper Y-boundary of search space
y_lb :: (float) Lower Y-boundary of search space
x_neighbor_distance :: (float) Distance between neighbors for X parameter
y_neighbor_distance :: (float) Distance between neighbors for Y parameter
RETURNS:
df :: (pandas dataframe) The search path of the algorithm in x, y, z (cost) coordinates
"""
print('\n' + HEADER)
print("Testing SimulatedAnnealing Module")
print(HEADER + '\n')
# 1 - 2. Initialize random solution and calculate cost
x_list = []
y_list = []
c_list = []
x_old = self._random_float(x_lb, x_ub, 12)
y_old = self._random_float(y_lb, y_ub, 12)
c_old = xy_function(x_old, y_old)
x_list.append(x_old)
y_list.append(y_old)
c_list.append(c_old)
print("Initial Cost = " + str(c_old))
# 3. Generate a new neighboring solution
t_new = self.start_temp
while t_new > self.stop_temp:
print(SPACER)
print('\n' + 'Running ' + str(self.num_sims) + ' simulations @ Temperature = ' + str(t_new) + '\n')
print(SPACER)
for i in range(self.num_sims): # TODO: Not very Pythonic...
print('\n' + 'Simulation Run #: ' + str(i + 1))
x_new = self._get_neighbor_float(current_value=x_old, distance=x_neighbor_distance, lower_bound=x_lb,
upper_bound=x_ub,
sig_dig=12)
y_new = self._get_neighbor_float(current_value=y_old, distance=y_neighbor_distance, lower_bound=y_lb,
upper_bound=y_ub,
sig_dig=12)
c_new = xy_function(x_new, y_new)
# Probability of acceptance
delta = c_new - c_old
print('delta = ' + str(delta))
if delta >= 0:
print('The new solution is better - moving to it!')
x_old = x_new
y_old = y_new
c_old = c_new
else:
print('The new solution is worse - rolling the dice to decide whether to accept it anyway...')
decision = self._roll_dice(delta=delta, t_new=t_new)
if decision == True:
print('The gods have spoken: selecting the new solution even though it is worse!')
x_old = x_new
y_old = y_new
c_old = c_new
else:
print(
'The gods have smiled on us: rejecting this worse solution and sticking with the old one!')
x_old = x_old
y_old = y_old
c_old = c_old
print('x_old = ' + str(x_old))
print('y_old = ' + str(y_old))
print('c_old = ' + str(c_old))
x_list.append(x_old)
y_list.append(y_old)
c_list.append(c_old)
print("New Cost = " + str(c_new))
t_new = t_new * self.alpha
print(FOOTER)
print('New Temperature = ' + str(t_new))
print(FOOTER)
dfx = pd.DataFrame(x_list)
dfx.columns = ['x']
dfy = pd.DataFrame(y_list)
dfy.columns = ['y']
dfc = pd.DataFrame(c_list)
dfc.columns = ['c']
results = pd.concat([dfx, dfy, dfc], axis=1)
return results
def goldstein_price_function(x, y):
""" Method for testing algorithm using the Goldstein-Price Function as the problem to optimize.
See wiki page for optimization functions: https://en.wikipedia.org/wiki/Test_functions_for_optimization
"""
cost = (1 + ((x + y + 1) ** 2) * (19 - 14 * x + 3 * (x ** 2) - 14 * y + 6 * x * y + 3 * (y ** 2))) * (
30 + ((2 * x - 3 * y) ** 2) * (18 - 32 * x + 12 * (x ** 2) + 48 * y - 36 * x * y + 27 * (y ** 2)))
return cost
def ackleys_function(x, y):
""" Method for testing algorithm using the Goldstein-Price Function as the problem to optimize.
See wiki page for optimization functions: https://en.wikipedia.org/wiki/Test_functions_for_optimization
"""
cost = -20 * math.exp((-0.2 * (math.sqrt(0.5 * (x ** 2 + y ** 2))))) - math.exp(
(0.5 * ((math.cos(2 * math.pi * x)) + math.cos(2 * math.pi * y)))) + math.exp(1) + 20
return cost
def plot_function_points(xy_function):
""" Generates a dataframe of x, y, z coordinates to """
x = np.linspace(-2, 2, 50)
y = np.linspace(-2, 2, 50)
x_list = []
y_list = []
cost_list = []
for j in range(len(x)): # TODO: Again, lots of non-pythonic stuff
x1 = x[j]
for p in range(len(y)): # TODO: Again, lots of non-pythonic stuff
y1 = y[p]
cost = xy_function(x1, y1)
x_list.append(x1)
y_list.append(y1)
cost_list.append(cost)
dfx = pd.DataFrame(x_list)
dfx.columns = ['x']
dfy = pd.DataFrame(y_list)
dfy.columns = ['y']
dfz = pd.DataFrame(cost_list)
dfz.columns = ['z']
function_data = pd.concat([dfx, dfy, dfz], axis=1)
return function_data
if __name__ == "__main__":
sa = SimulatedAnnealing(start_temp=1000, stop_temp=1, alpha=0.95, num_sims=250)
results = sa.run_annealing(xy_function=goldstein_price_function, x_ub=2.0001, x_lb=-2.0001, y_ub=2.0001,
y_lb=-2.0001, x_neighbor_distance=0.1000000, y_neighbor_distance=0.1000000)
function_data = plot_function_points(goldstein_price_function)
trace1 = go.Scatter3d(
x=results['x'],
y=results['y'],
z=results['c'],
mode='markers',
name='Optimization Path',
marker=dict(
size=9,
color=results['c'],
colorscale='Rainbow',
opacity=0.95
)
)
trace2 = go.Scatter3d(
x=function_data['x'],
y=function_data['y'],
z=function_data['z'],
mode='markers',
name='Function Surface',
marker=dict(
size=6,
color=function_data['z'],
colorscale='Blues',
opacity=0.65
)
)
data = [trace2, trace1]
layout = go.Layout(
autosize=True,
margin=dict(l=0, r=0, b=0, t=0),
showlegend=True,
title=' Simulated Annealing Algorithm ',
xaxis=dict(title='X'),
yaxis=dict(title='Y'),
font=dict(size=15)
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='3d-scatter-colorscale')
