فرادرس
محاسبات تکاملی چیست؟ — به زبان ساده
در این مطلب، با مبحث «محاسبات تکاملی» (Evolutionary Computation)، مفاهیم این حوزه و مهم‌ترین الگوریتمهای تکاملی آشنا خواهید شد. روش‌های محاسبات تکاملی، محققان و فعالان حوزه هوش مصنوعی و «بهینهسازی عددی» (Numerical Optimization) را قادر می‌سازند تا از ایده فرایندهای تکاملی (Evolutionary Process) و شبیه‌سازی (Simulation) آن‌ها برای حل مسائل جهان واقعی استفاده کنند؛ مسائلی که شاید پیش از این برای حل آن‌ها، راهکار امکان‌پذیر (Feasible) و معقولی وجود نداشت.
اولین مفهومی که برنامه‌نویسان و یا توسعه‌دهندگان برنامه‌های کاربردی با آن دست و پنجه نرم می‌کنند، مفهوم «الگوریتم» (Algorithm) است. وقتی که کاربر یا یک برنامه‌نویس به دنبال راه حل برای یک مسأله (به عنوان نمونه، یک مسأله بهینهسازی (Optimization)) است، یک استراتژی یا مجموعه دقیقی از دستورالعمل‌های لازم برای حل مسأله مورد نظر را مشخص می‌کند که به آن الگوریتم گفته می‌شود. حال سناریویی را فرض کنید که در آن مسأله داده شده به قدری پیچیده باشد که حل آن توسط الگوریتمهای مرسوم امکان‌پذیر نباشد. در چنین حالتی، چگونه می‌توان استراتژی لازم برای حل این مسأله (الگوریتم حل مسأله) را کد نویسی کرد؟
این سناریو، یکی از حوزه‌های اصلی کاربرد «هوش مصنوعی» (Artificial Intelligence) در حل مسائل جهان واقعی محسوب می‌شود. به عبارت دیگر، زمانی می‌توان از پتانسیل کامل الگوریتمهای هوش مصنوعی بهره‌برداری کرد که الگوریتمهای مرسوم حل مسأله پاسخگوی نیازهای مسأله مورد نظر نباشند و برای حل کردن این دسته از مسائل، روش‌های بدیع حل مسأله با استفاده از تکنیک‌های هوش مصنوعی نیاز باشد.
یکی از مقرون به صرفه‌ترین و ساده‌ترین تکنیک‌های حل مسأله (از لحاظ بار محاسباتی و زمان لازم برای اجرای الگوریتم) در حوزه هوش مصنوعی، روش‌های محاسبات تکاملی هستند. به طور کلی، الگوریتمهای محاسبات تکاملی بر پایه به‌کارگیری «نظریه تکامل داروین» (Darwin’s Theory of Evolution) جهت پیادهسازی برنامه‌های کامپیوتری شکل گرفته‌اند.
یکی از اهداف مهم روش‌های محاسبات تکاملی و الگوریتمهای تکاملی به طور خاص، بهبود کیفیت راه حل‌های ضعیف تولید شده برای یک مسأله داده شده است. جهت بهبود کیفیت راه حل‌های ضعیف تولید شده، الگوریتمهای محاسبات تکاملی از فرایندهای تکاملی نظیر «جهش» (Mutation) و سایر موارد استفاده می‌کنند؛ به عبارت دیگر، الگوریتمهای محاسبات تکاملی، در یک فرایند تکراری (Iterative Process)، آنقدر راه حل‌های ضعیف تولید شده را با استفاده از عملگرهایی نظیر جهش (Mutation) دستکاری می‌کنند تا سیستم بتواند با دقت (Accuracy) مطلوبی مسأله مورد نظر را حل کند.
محاسبات تکاملی
در حوزه «علوم کامپیوتر» (Computer Science) و هوش مصنوعی، محاسبات تکاملی خانواده‌ای از الگوریتم‌ها جهت «بهینهسازی سراسری» (General Optimization) هستند که از فرایندهای «تکامل زیستی» (Biological Evolution) الهام گرفته شدهاند. به عبارت دیگر، به زیر شاخه‌ای از هوش مصنوعی و «محاسبات نرم» (Soft computing) که به مطالعه و پیادهسازی الگوریتمهای الهام گرفته شده از فرایندهای تکامل زیستی می‌پردازد، الگوریتمهای محاسبات تکاملی گفته می‌شود.
از دیدگاه فنی، الگوریتمهای محاسبات تکاملی خانواده‌ای از روش‌های حل مسأله محسوب می‌شوند که مبتنی بر جمعیت (Population-based) و آزمون و خطا (Trial and Error) هستند و از مکانیزم‌های بهینهسازی تصادفی (Stochastic Optimization) یا بهینهسازی فرا اکتشافی (Meta-Heuristic) جهت همگرایی به جواب بهینه سراسری یا تقریبی (Approximation) از جواب بهینه استفاده می‌کنند.
در محاسبات تکاملی، ابتدا یک مجموعه ابتدایی متشکل از «جواب‌های کاندید» (Candidate Solutions) تشکیل می‌شود. در طول فرایند تکاملی، الگوریتمهای محاسبات تکاملی با دستکاری و به‌روزرسانی جمعیت متشکل از جواب‌های کاندید، جمعیت را به سمت ناحیه حاوی جواب «بهینه سراسری» (Global Optimum) حرکت می‌دهند. در هر تکرار از الگوریتمهای محاسبات تکاملی (که به آن «نسل» (Generation) نیز گفته می‌شود)، از طریق حذف کردن جواب‌های نامطلوب در جمعیت و ایجاد تغییرات بسیار کوچک و البته تصادفی در جواب‌های کاندید، فرایند تکاملی شکل خواهد گرفت.
با الگو گرفتن از فرایندهای تکامل طبیعی در زیست‌شناسی، جمعیت متشکل از جواب‌های کاندید (در الگوریتمهای محاسبات تکاملی)، تحت تاثیر فرایندهای تکاملی نظیر «انتخاب طبیعی» (Natural Selection) و جهش قرار می‌گیرد؛ در واژه‌شناسی الگوریتمهای محاسبات تکاملی، به فرایند انتخاب طبیعی، فرایند انتخاب مصنوعی (Artificial Selection) نیز گفته می‌شود. در نتیجه، بر اساس مکانیزم‌های تعریف شده در فرایند تکامل، جمعیت متشکل از جواب‌های کاندید (در الگوریتمهای محاسبات تکاملی) به نحوی تکامل پیدا می‌کنند که با مرور زمان و گذر نسل‌های متوالی، «برازندگی» (Fitness) آن‌ها افزایش پیدا کند؛ از «تابع برازندگی» (Fitness Function) برای محاسبه برازندگی جواب‌های کاندید در الگوریتمهای محاسبات تکاملی استفاده می‌شود.
روش‌های محاسبات تکاملی قادر هستند تا مجموعه‌ای از جواب‌های بهینه (Optimized Solutions) را برای یک مسأله خاص و در شرایط مختلف آن تولید نمایند؛ چنین ویژگی مهمی در سیستم‌های محاسبات تکاملی و الگوریتمهای تکاملی، آن‌ها را در نقطه مقابل روش‌های بهینهسازی مرسومی قرار می‌دهد که قادر هستند تنها یک جواب قطعی (Deterministic Solutions) و یا تعداد محدودی جواب تقریبی (Approximated Solutions) برای مسأله مورد نظر تولید نمایند. علاوه بر این، قابلیت تولید مجموعه‌ای از جواب‌های کاندید برای یک مسأله مورد نظر، الگوریتمهای محاسبات تکاملی را به یکی از محبوب‌ترین روش‌های حل مسأله در حوزه علوم کامپیوتر تبدیل کرده است.
تاکنون نسخه‌های مختلفی از الگوریتمهای محاسبات تکاملی ارائه شده است. بسیاری از الگوریتمهای محاسبات تکاملی که در سال‌های اخیر ارائه شدهاند، «مستقل از دامنه» (Domain-independent) و «مستقل از مسأله» (Problem-independent) هستند که آن‌ها را به گزینه بسیار مناسبی برای حل دامنه وسیعی از مسائل، به ویژه مسائل و ساختارهای داده‌ای (Data Structures) خاص، تبدیل می‌کند. بعضا از الگوریتمهای محاسبات تکاملی، به عنوان یک روش آزمایش کامپیوتری (In Silico Experimental Procedure)، جهت مطالعه جنبه‌های مشترک فرایندهای تکاملی عمومی استفاده می‌شود.
تکامل، محاسبات تکاملی و مفاهیم مهم
هدف از پیادهسازی الگوریتمهای محاسبات تکاملی (Evolutionary Computation)، شبیه‌سازی فرایند تکامل در یک سیستم کامپیوتری است. نتیجه شبیه‌سازی فرایند تکامل، تولید مجموعه‌ای از الگوریتمهای بهینهسازی (Optimization Algorithm) است که معمولا مبتنی بر یک مجموعه ساده از ویژگی‌های مشخصه (ژنها) و دستکاری آن‌ها در یک فرایند تکراری و تکاملی هستند. ویژگی مهم الگوریتمهای محاسبات تکاملی این است که در هر تکرار از فرایند تکامل، به صورت تدریجی، کیفیت جواب‌های تولید شده برای یک مسأله بهینهسازی بهبود بخشیده می‌شود و در نهایت، یک جواب بهینه (یا حداقل یک تقریب مناسب از جواب بهینه) حاصل می‌شود.
همانطور که پیش از این نیز اشاره شد، ایده اصلی محاسبات تکاملی بر پایه نظریه تکامل داروین (Darwin’s Theory of Evolution) بنا نهاده شده است. اصول مهم در نظریه تکامل داروین عبارتند از:
- «بقای برازنده‌ترین‌ها» (Survival of the Fittest). بر مبنای نظریه تکامل داروین، نمونه‌های موجود در یک محیط (طبیعت برای موجودات زنده نقش محیط را ایفا می‌کند) با گذشت زمان خود را با شرایط محیط وفق نمی‌دهند. بلکه، در هر نسل تنها آن دسته از نمونه‌هایی که برازندگی بیشتری نسبت به دیگر نمونه‌ها دارند باقی می‌مانند و به بقای خود ادامه می‌دهند.
- انتخاب بر مبنای فنوتایپ (Phenotype).
- به ارث بردن ژنوتایپ (Genotype) نمونه‌های والد توسط نمونه‌های فرزند.
- تولید مثل (Reproduction).
- تغییرات تصادفی در ژن‌های نمونه‌های موجود در محیط.
نظریه تکامل داروین از چهار فرضیه اصلی تشکیل شده است:
- نمونه‌های موجود در یک جمعیت یا گونه‌های جاندار، تفاوت‌های معناداری با یکدیگر دارند. اگر بخواهیم این فرضیه را در قالب الگوریتمهای محاسبات تکاملی تصویر کنیم، به این نتیجه خواهیم رسید که نمونه‌های موجود در جمعیت اولیه تولید شده در یک الگوریتم تکاملی باید ویژگی‌ها یا مقادیر متغیری متفاوت از یکدیگر داشته باشند. چنین فرضی به جمعیت اولیه تولید شده کمک می‌کند تا بتوانند در فضای جستجوی مسأله پراکنده شود و بیشتر مناطق موجود در این فضا را پوشش دهد. از آنجایی که مکان جواب بهینه سراسری در فضای جستجوی مسأله مشخص نیست، پراکنده شدن نمونه‌ها در مناطق موجود در جمعیت، احتمال رسیدن به جواب بهینه سراسری (یا تقریبی از آن) را افزایش می‌دهد.
- در طول فرایند تکامل و در گذار (Transition) از هر نسل به نسل بعدی، برخی از ویژگی‌های موجودات زنده به فرزندان (Offspring | Child) منتقل می‌شوند. برای شبیه‌سازی چنین فرایندی در تکامل طبیعی از عملگرهایی نظیر تولید مثل (Reproduction)، جهش و ترکیب یا آمیزش (Recombination | Crossover) استفاده می‌شود. با استفاده از عملگر تولید مثل، یک نمونه کپی برابر با اصل از نمونه والد ایجاد می‌شود. عملگر جهش نیز از طریق اعمال تغییرات جزئی و تصادفی در ژن‌های نمونه‌های والد، سبب تولید نمونه‌های فرزند جدید در جمعیت می‌شود. علاوه بر این، از طریق عملگر ترکیب یا آمیزش، دو نمونه والد با یکدیگر ترکیب می‌شوند و هر یک از فرزندان ایجاد شده، ژن‌های والدین را به طور تصادفی به ارث می‌برند.
- در هر نسل (تکرار) از فرایند تکامل، تعداد نمونه‌های فرزند ایجاد شده از تعداد نمونه‌هایی که زنده خواهند ماند، بیشتر خواهد بود. در الگوریتمهای محاسبات تکاملی، از فرایندی به نام «انتخاب» (Selection) برای مشخص کردن نمونه‌هایی که باید از نسل فعلی به نسل بعدی منتقل شوند استفاده می‌شود. در الگوریتمهای محاسبات تکاملی روش کار بدین صورت که نمونه‌های برازنده‌تر شانس (یا احتمال) بیشتری برای انتخاب شدن و قرار گرفتن در جمعیت نسل بعد خواهند داشت.
- «بقاء» (Survival) و تولید مثل نمونه‌ها به صورت تصادفی انجام نمی‌شود. نمونه‌هایی که باقی می‌مانند و شروع به تولید مثل می‌کنند (و یا نمونه‌هایی که نرخ تولید مثل بالاتری نسبت به دیگر نمونه‌ها دارند)، نمونه‌هایی هستند که ویژگی‌ها یا مقادیر متغیر مطلوب‌تری نسبت به دیگر نمونه‌ها دارند؛ به عبارت دیگر، در ناحیه‌ای از فضای جستجو قرار دارند که به احتمال زیاد به جواب بهینه سراسری نزدیک‌تر هستند. به چنین فرایند، انتخاب طبیعی (Natural Selection) گفته می‌شود.
با توجه به اصول و فرضیه‌های مطرح شده در محاسبات تکاملی، یک الگوریتم تکاملی از چهار مؤلفه اصلی تشکیل خواهد شد:
- مؤلفه «جمعیت» (Population) که مجموعه نمونه‌های موجود در جمعیت را مدل‌سازی می‌کند.
- مؤلفه «عملگرهای تکاملی» (Evolutionary Operators) که سبب تغییر کدهای ژنتیکی نمونه‌های موجود در جمعیت می‌شود. همچنین این مؤلفه سبب افزایش «تنوع» (Diversity) در جواب‌های کاندید تولید شده می‌شود.
- مؤلفه برازندگی که کیفیت جواب‌های کاندید تولید شده (نزدیکی یا همگرایی آن‌ها به جواب بهینه سراسری) را می‌سنجد.
- مؤلفه انتخاب (Selection) که اصل بقای برازنده‌ترین‌ها (Survival of the Fittest) را در الگوریتمهای محاسبات تکاملی شبیه‌سازی می‌کند.
در ادامه، با مهم‌ترین مفاهیم موجود در حوزه محاسبات تکاملی و شبیه‌سازی فرایند تکامل آشنا خواهید شد.
انتخاب طبیعی (Natural Selection)
همانطور که پیش از این نیز اشاره شد، یکی از اصول اساسی الگوریتمهای محاسبات تکاملی (الگوریتمهای تکاملی) بقای برازنده‌ترین‌ها (Survival of the Fittest) است. به عبارت دیگر، بقاء در طبیعت بسیار سخت است و موجوداتی که می‌تواند به بقای خود در طبیعت ادامه دهند، شانس بیشتری برای تولید مثل خواهند داشت. محیط زندگی موجودات زنده (طبیعت)، به طور طبیعی موجوداتی را که از بیشترین برازندگی برخوردار هستند، برای تولید مثل انتخاب می‌کند و باقی موجوداتی را که قادر به بقا نیستند از بین می‌برد.
نمونه مهم چنین فرایندی در مورد زرافه‌ها کاملا مشهود است. گردن درازتر به زرافه کمک می‌کند تا بتواند از شاخه‌های بالاتر تغذیه کند. به مرور زمان، ظاهرا چنین ویژگی در زرافه‌ها موجب شد تا زرافه‌هایی که گردن درازتری دارند از شانس بیشتر برای بقاء برخوردار باشند؛ به عبارت دیگر، هیچ نیروی مستقیمی در طبیعت وجود نداشت که سبب درازتر شدن گردن زرافه‌ها شود. بلکه، زرافه‌هایی که به طور طبیعی از گردن درازتری برخوردار بودند، شانس بیشتری برای بقاء در طبیعت و تولید مثل پیدا می‌کردند.
مکانیزم مشابه با انتخاب طبیعی را می‌توان در برنامه‌های کامپیوتری و جهت پیادهسازی الگوریتمهای محاسبات تکاملی مورد استفاده قرار داد. اگر سیستم محاسبات تکاملی یک جواب تقریبی (Approximate Solution) برای یک مسأله بهینهسازی در اختیار داشته باشد، با ایجاد تغییرات تصادفی در جواب و محاسبه برازندگی جواب‌های جدید می‌توان مشخص کرد که آیا تغییرات ایجاد شده، سبب بهبود کیفیت جواب‌ها شده است یا نه. در صورتی که چنین فرایندی به صورت متوالی و تکراری انجام شود، به احتمال زیاد در هر مرحله، به حداقل یک جواب بهتر (با برازندگی بیشتر) یا برابر دست پیدا خواهد شد. انتخاب طبیعی یکی از حیاتی‌ترین مؤلفه‌های محاسبات تکاملی محسوب می‌شود که قوه محرکه آن عملگرهای تکاملی نظیر جهش تصادفی در ژنها (متغیرها) است.
فنوتایپ (Phenotype) و ژنوتایپ (Genotype)
جهت درک بهتر چگونگی شبیه‌سازی فرایندهای تکامل طبیعی در الگوریتمهای محاسبات تکاملی، ابتدا نیاز است تا نقش تکامل در زیست‌شناسی مشخص شود. در طبیعت، تمامی موجودات از شاکله (بدن | Body) و مجموعه‌ای از رفتارها تشکیل شدهاند. به این ویژگی‌ها، فنوتایپ (Phenotype) آن موجود زنده گفته می‌شود؛ به عبارت دیگر، به شکل ظاهر و رفتاری یک موجود زنده فنوتایپ گفته می‌شود. رنگ مو، چشم و پوست، همگی بخش از فنوتایپ (Phenotype) موجودات زنده هستند.
شکل ظاهری موجودات زنده توسط مجموعه‌ای از دستورالعمل‌های کدبندی شده (Encoded) در سلول‌های آن‌ها مشخص می‌شود. به این مجموعه دستورالعمل‌های کدبندی شده، ژنوتایپ (Genotype) گفته می‌شود. به عبارت دیگر، ژنوتایپ به اطلاعاتی اطلاق می‌شود که در DNA موجودات زنده کدبندی شده است.با اینکه فنوتایپ شکل ظاهری موجودات زنده پس از پدید آمدن را مشخص می‌کند، ژنوتایپ موجودات زنده همان طرح (Blueprint) ابتدایی است که شکل نهایی طاهر موجودات زنده از آن مشتق شده است.
دلیل اینکه فنوتایپ و ژنوتایپ در موجودات زنده، به عنوان دو مفهوم جدا از یکدیگر شناخته می‌شوند، بسیار ساده است. محیط (طبیعت نقش محیط را برای موجودات زنده ایفا می‌کند) نقش مهمی در شکل‌گیری ظاهر موجودات زنده دارد. به عنوان نمونه، در صورتی که دو خانه، با طرح (BluePrint) یکسان ولی با بودجه‌های متفاوت، ساخته شوند، بدون شک شکل و ظاهر تفاوتی از یکدیگر پیدا خواهند کرد.
در اغلب شرایط، این محیط است که موفقیت ژنوتایپ‌ها را مشخص می‌کند. به عبارت دیگر، موجودی در محیط موفق است که بتواند به بقای خود ادامه دهد و ژنوتایپ‌های خود را از طریق تولید مثل به فرزندان (Offspring | Child) خود منتقل کند. اطلاعات لازم برای طراحی شاکله و رفتار موجودات زنده در DNA آن‌ها نقش بسته است. هر بار که موجودات زنده تولید مثل می‌کنند، DNA آن‌ها کپی و به فرزندانشان منتقل می‌شود.
در این میان و در حین انجام فرایند کپی شدن DNA والدین و انتقال به فرزندان ممکن است جهش‌های تصادفی در DNA رخ بدهد که سبب ایجاد تغییراتی در DNA فرزندان شود. چنین تغییراتی پتانسیل ایجاد تغییر در فنوتایپ موجودات زنده را دارند.
در الگوریتمهای محاسبات تکاملی نظیر الگوریتم ژنتیک (Genetic Algorithm)، به جمعیت جواب‌های کاندید یک مسأله بهینهسازی که به سمت جواب بهینه همگرا می‌شوند، فنوتایپ (Phenotype) گفته می‌شود. همچنین، هر کدام از جواب‌های کاندید، مجموعه‌ای از ویژگی‌های مختص به خود دارند که از طریق اعمال عملگرهای تکاملی تغییر پیدا می‌کند؛ به این مجموعه از ویژگی‌ها (مقادیر متغیرهای یک نمونه)، ژنوتایپ گفته می‌شود.
ساختارهای الگوریتمهای محاسبات تکاملی
بیشتر الگوریتمهای محاسبات تکاملی، از طریق همانندسازی مکانیزم‌های تکامل طبیعی نظیر انتخاب طبیعی، اقدام به بهینهسازی مسائل مختلف می‌کنند. ساختار کلی الگوریتمهای محاسبات تکاملی در شکل زیر نمایش داده شده است:
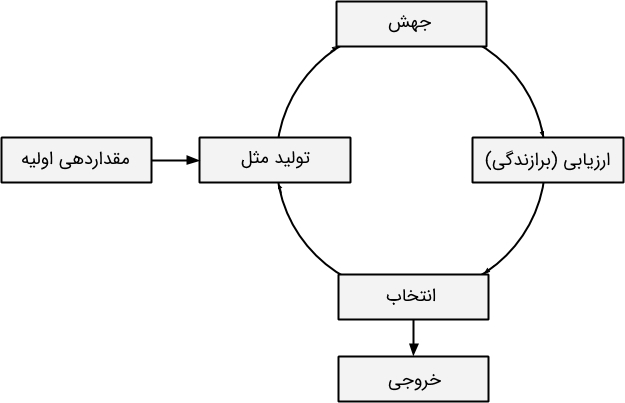
- مقداردهی اولیه: برای اینکه بتوان فرایندهای تکاملی را در الگوریتم محاسبات تکاملی شبیه‌سازی کرد نیاز است تا ابتدا جمعیتی از جواب‌های کاندید اولیه (ابتدایی) تولید شود. در برخی از کاربردها و مسائل مختلف، انتخاب مقادیر اولیه مناسب بسیار مهم است؛ زیرا، مقادیر اولیه متفاوت ممکن است منجر به تولید جواب‌های بهینه کاملا متفاوت شود.
- تولید مثل: در این مرحله از فرایند تکامل در الگوریتمهای محاسبات تکاملی، تعداد کپی‌های زیادی از جواب کنونی تولید می‌شود.
- جهش: در این مرحله از فرایند تکامل در الگوریتمهای محاسبات تکاملی، عملیات جهش روی هر یک از نمونه‌های کپی ایجاد شده انجام می‌شود. به جرات می‌توان گفت که یکی از مهم‌ترین مؤلفه‌های الگوریتمهای محاسبات تکاملی جهش است؛ زیرا سرعت همگرایی الگوریتم به جواب بهینه را کنترل می‌کند.
- ارزیابی (برازندگی): در این مرحله، برازندگی هر یک از نمونه‌های (جواب‌های کاندید) موجود در جمعیت ارزیابی می‌شود تا کیفیت آن‌ها مشخص شود؛ به عبارت دیگر، میزان نزدیکی یا همگرایی نمونه‌ها یا جواب‌های کاندید به جواب بهینه سراسری مشخص می‌شود.
- انتخاب: در این مرحله و پس از اینکه برازندگی نمونه‌های موجود در جمعیت مشخص شد، تنها بهترین نمونه‌ها انتخاب می‌شوند و در تولید نسل بعدی الگوریتمهای محاسبات تکاملی شرکت می‌کنند.
- خروجی: همانطور که پیش از این نیز اشاره شد، تکامل یک فرایند تکراری است ولی این فرایند یا به تعداد دفعات مشخص تکرار می‌شود و یا تا جایی ادامه پیدا می‌کند که در تکرارهای متوالی، دیگر تغییرات محسوسی در برازندگی بهترین نمونه‌ها ایجاد نشود. در این مرحله از فرایند تکامل در الگوریتمهای محاسبات تکاملی، شرط توقف الگوریتم محاسبات تکاملی بررسی می‌شود و در صورت برقرار بودن شرط، بهترین جواب‌های کاندید تولید شده در خروجی نمایش داده می‌شوند.
بهینه محلی (Local Optimum | Local Maximum | Local Minimum)
کاری که فرایندهای تکاملی انجام می‌دهند این است که برازندگی جمعیت متشکل از جواب‌های کاندید را افزایش می‌دهند. به عبارت دیگر، در الگوریتمهای محاسبات تکاملی یک تابع برازندگی برای مسأله تعریف شده است. هدف الگوریتمهای تکاملی پیدا کردن نقطه بهینه این تابع است (در مسائل کمینه‌سازی هدف پیدا کردن نقطه کمینه تابع برازندگی و هدف مسائل بیشنه‌سازی، پیدا کردن نقطه بیشینه تابع برازندگی است). با این حال، شکل و توزیع تابع برازندگی مشخص نیست. تنها کاری که الگوریتمهای بهینهسازی می‌توانند انجام دهند این است که جواب‌های جدیدی را اطراف نقطه‌ای که بهترین جواب کاندید یافت شده در آن قرار دارد، نمونهگیری (Sampling) کنند.
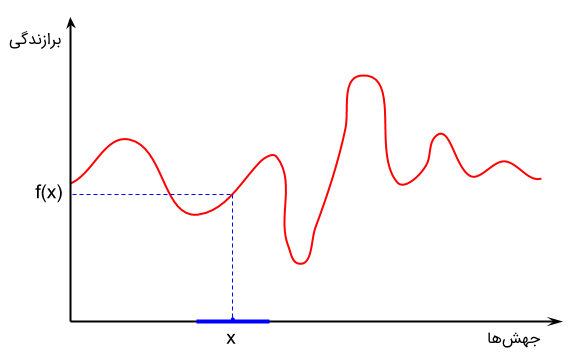
شکل بالا نشان می‌دهد که جهش‌های مختلف ایجاد شده در نمونه‌های جمعیت (در محور افقی)، سبب تولید امتیازات برازندگی متفاوت (در محور عمودی) خواهد شد. کاری که الگوریتمهای محاسبات تکاملی انجام می‌دهند این است که با هدف افزایش برازندگی جواب‌های کاندید، نمونه‌های جدیدی را در همسایگی محلی (Local Neighborhood) نقطه X نمونهگیری می‌کنند. بسته به اندازه همسایگی انتخاب شده، تعداد نسل‌های (تکرار) متفاوتی نیاز است تا الگوریتم بتواند به نقطه بهینه سراسری همگرا شود.
در صورتی که اندازه همسایگی کوچکی انتخاب شود، الگوریتم محاسبات تکاملی در دام بهینه محلی (کمینه یا بیشینه محلی) گرفتار خواهد شد. بهینه‌های محلی، جواب‌های کاندیدی هستند که بهترین جواب در همسایگی محلی محسوب می‌شوند ولی نه به صورت سراسری. برخی از توابع بهینهسازی ممکن است حاوی بهینه‌های محلی متعددی باشند ولی تنها یک بهینه سراسری داشته باشند. در حالتی که الگوریتم در بهینه محلی گرفتار شود قادر نخواهد بود تا جواب بهتری برای مسأله بهینهسازی پیدا کند.
الگوریتمهای مبتنی بر محاسبات تکاملی
در حوزه «هوش مصنوعی» (Artificial Intelligence)، یک الگوریتم تکاملی (Evolutionary Algorithm) زیر مجموعه‌ای از خانواده روش‌های هوش محاسباتی است. بنابراین، الگوریتم تکاملی را می‌توان یک الگوریتم فرا اکتشافی و مبتنی بر جمعیت برای حل مسائل بهینهسازی به شمار آورد. یک الگوریتم تکاملی از مکانیزم‌هایی استفاده می‌کند که از فرایندهای تکامل زیستی نظیر «تولید مثل» (Reproduction)، جهش، ترکیب یا آمیزش و انتخاب الهام گرفته شدهاند. به فرایندهای تکامل زیستی در محاسبات تکاملی، «عملگرهای تکاملی» (Evolational Operators) گفته می‌شود.
در الگوریتمهای مبتنی بر محاسبات تکاملی (الگوریتمهای تکاملی)، جواب‌های کاندید برای یک مسأله بهینهسازی نقش «نمونه‌ها» (Individuals) در یک جمعیت (Population) را ایفا خواهند کرد. تابع برازندگی نیز کیفیت جواب‌های کاندید تولید شده را مشخص می‌کند. «تکامل جمعیت» (Evolution of Population) زمانی حاصل می‌شود که در یک فرایند تکراری و در نسل‌های متوالی از الگوریتم تکاملی، عملگرهای تکاملی روی نمونه‌های موجود در جمعیت اعمال و جمعیت به سمت ناحیه حاوی جواب بهینه سراسری مسأله بهینهسازی همگرا شود.
ویژگی‌های الگوریتمهای مبتنی بر محاسبات تکاملی
از آنجایی که الگوریتمهای مبتنی بر محاسبات تکاملی (الگوریتمهای تکاملی) هیچ فرضی در مورد تابع برازندگی (جهت مشخص کردن کیفیت جواب‌های کاندید) انجام نمی‌دهند، عملکرد بسیار خوبی در تقریب زدن جواب‌های دامنه وسیعی از مسائل بهینهسازی از خود نشان می‌دهند. در الگوریتمهای تکاملی، با در اختیار داشتن یک مسأله، از فرایند «تکامل طبیعی» (Natural Evolution) به عنوان الگویی برای پیادهسازی استراتژی‌های لازم جهت یافتن جواب‌های بهینه و یا «تقریبا بهینه» (Near Optimum) مسأله داده شده استفاده می‌شود. همانطور که پیش از این نیز اشاره شد، تکامل زمانی اتفاق می‌افتد که عملگرهای تکاملی روی جواب‌های کاندید اعمال می‌شوند و با تغییر کدهای ژنتیکی (یا مقادیر متغیرهای) جواب‌های کاندید، جمعیت را به سمت نقطه بهینه سراسری (و یا تقریب مناسبی از آن) سوق می‌دهند.
یکی از ویژگی‌های مهم الگوریتمهای محاسبات تکاملی این است که در یافتن جواب‌های بهینه (یا تقریب مناسبی از جواب‌های بهینه) مسائل بهینهسازی، عملکرد بسیار خوبی از خود نشان می‌دهند. دسته‌ای از مسائل که جهت بهینهسازی آن‌ها از الگوریتمهای محاسبات تکاملی استفاده می‌شود، «مسائل بهینهسازی ترکیبیاتی» (Combinatorial Optimization Problems) نام دارند که از لحاظ محاسباتی بسیار سخت و پیچیده هستند؛ انتظار می‌رود که زمان محاسباتی لازم برای بهینهسازی چنین مسائلی، با زیاد شدن ابعاد (اندازه) مسأله، به طور نمایی افزایش پیدا کند.
به عنوان نمونه، «مسأله فروشنده دوره‌گرد» (Travelling Salesman Problem) یکی از مسائل بهینهسازی ترکیبیاتی محسوب می‌شود. در الگوریتمهای مرسوم ارائه شده برای حل مسأله فروشنده دوره‌گرد، پیش از این که بتوان یکی از مسیرهای موجود در فضای جستجوی مسأله را به عنوان مسیر بهینه انتخاب کرد، باید تعداد قابل توجهی از مسیرهای ممکن میان شهر پیمایش و ارزیابی شوند. حالا فرض کنید که تعداد شهرهای موجود در مسأله یک عدد بسیار بزرگ باشد.
در چنین حالتی، تعداد گام‌های محاسباتی لازم برای پیدا کردن جواب بهینه، با افزایش تعداد شهرهای موجود در فضای مسأله، به طور نمایی افزایش پیدا می‌کند. در نتیجه، افزایش تعداد شهرها در فضای جستجوی مسأله سبب می‌شود تا اختصاص دادن قدرت محاسباتی لازم برای پیدا کردن جواب بهینه، حتی روی کامپیوترهای قدرتمند امروزی، عملا غیر ممکن شود. بنابراین، بسیاری از الگوریتمهای مرسوم جهت حل چنین مسائلی، به جای اینکه به دنبال جواب بهینه برای مسائل بهینهسازی ترکیبیاتی سخت باشند، به یافتن یک تقریب از جواب بهینه بسنده می‌کنند.
مسأله فروشنده دوره‌گرد را به راحتی می‌توان با استفاده از الگوریتمهای محاسبات تکاملی (به عنوان نمونه، الگوریتم ژنتیک (Genetic Algorithm)) و به شکل به مراتب بهینه‌تری نسبت به روش‌های مرسوم حل مسأله، بهینهسازی کرد. برای چنین کاری، از ساختاری که در ادامه نمایش داده شده است استفاده می‌شود:
- در ابتدا، جمعیتی متشکل از جواب‌های کاندید (تعدادی شهر که بر اساس یک ترتیب تصادفی (یا شبه تصادفی) در فضای جستجوی مسأله تولید شدهاند)، به عنوان جمعیت اولین نسل در فرایند تکاملی الگوریتم ژنتیک، تولید می‌شود.
- برازندگی هر یک از نمونه‌های موجود در جمعیت (که نقش یک جواب کاندید برای مسأله مورد نظر را ایفا می‌کنند) محاسبه می‌شود.
- زمانی که قرار است جمعیت نسل بعد مشخص شود، بهترین نمونه‌های موجود در جمعیت (یا نمونه‌هایی که کمترین مسافت لازم را برای پیمایش می‌طلبند) نگه‌داری و نمونه‌هایی که برازندگی کمتری دارند، نادیده گرفته می‌شوند.
- علاوه بر نمونه‌هایی که بیشترین برازندگی را دارند (نمونه‌هایی که در هر نسل نگه‌داری می‌شوند)، از نمونه‌های جدیدی که به آن‌ها نمونه‌های فرزند (Offspring | Child) نیز گفته می‌شود جهت تشکیل جمعیت نسل بعد استفاده می‌شود.
- نمونه‌های فرزند، معمولا از طریق اعمال عملگر جهش روی نمونه‌های والد (Parents) ایجاد می‌شوند. همچنین، از عملگرهای تکاملی نظیر ترکیب یا آمیزش جهت تولید نمونه‌های فرزند استفاده می‌شود؛ در این عملگر، ژن‌های تشکیل دهنده دو نمونه والد با یکدیگر ترکیب می‌شوند و فرزندان حاصل، ویژگی‌های ژنی نمونه‌های والد را به ارث می‌برند.
در ادامه کدهای پیادهسازی الگوریتم ژنتیک، جهت حل مسأله فروشنده دوره‌گرد، در زبان‌های متلب و پایتون نمایش داده شده است. الگوریتمهای محاسبات تکاملی، با استفاده از فرایند تکاملی تصادفی قادر هستند تا با سرعت به مراتب بهتری به جواب بهینه مسأله یا تقریب مناسبی از آن دست پیدا کنند.
کدهای لازم برای حل مسأله فروشنده دوره‌گرد با استفاده از زبان برنامه‌نویسی متلب:
function varargout = tsp_ga(varargin)
% Initialize default configuration
defaultConfig.xy = 10*rand(50,2);
defaultConfig.dmat = [];
defaultConfig.popSize = 100;
defaultConfig.numIter = 1e4;
defaultConfig.showProg = true;
defaultConfig.showResult = true;
defaultConfig.showWaitbar = false;
% Interpret user configuration inputs
if ~nargin
userConfig = struct();
elseif isstruct(varargin{1})
userConfig = varargin{1};
else
try
userConfig = struct(varargin{:});
catch
error('Expected inputs are either a structure or parameter/value pairs');
end
end
% Override default configuration with user inputs
configStruct = get_config(defaultConfig,userConfig);
% Extract configuration
xy = configStruct.xy;
dmat = configStruct.dmat;
popSize = configStruct.popSize;
numIter = configStruct.numIter;
showProg = configStruct.showProg;
showResult = configStruct.showResult;
showWaitbar = configStruct.showWaitbar;
if isempty(dmat)
nPoints = size(xy,1);
a = meshgrid(1:nPoints);
dmat = reshape(sqrt(sum((xy(a,:)-xy(a',:)).^2,2)),nPoints,nPoints);
end
% Verify Inputs
[N,dims] = size(xy);
[nr,nc] = size(dmat);
if N ~= nr || N ~= nc
error('Invalid XY or DMAT inputs!')
end
n = N;
% Sanity Checks
popSize = 4*ceil(popSize/4);
numIter = max(1,round(real(numIter(1))));
showProg = logical(showProg(1));
showResult = logical(showResult(1));
showWaitbar = logical(showWaitbar(1));
% Initialize the Population
pop = zeros(popSize,n);
pop(1,:) = (1:n);
for k = 2:popSize
pop(k,:) = randperm(n);
end
% Run the GA
globalMin = Inf;
totalDist = zeros(1,popSize);
distHistory = zeros(1,numIter);
tmpPop = zeros(4,n);
newPop = zeros(popSize,n);
if showProg
figure('Name','TSP_GA | Current Best Solution','Numbertitle','off');
hAx = gca;
end
if showWaitbar
hWait = waitbar(0,'Searching for near-optimal solution ...');
end
for iter = 1:numIter
% Evaluate Each Population Member (Calculate Total Distance)
for p = 1:popSize
d = dmat(pop(p,n),pop(p,1)); % Closed Path
for k = 2:n
d = d + dmat(pop(p,k-1),pop(p,k));
end
totalDist(p) = d;
end
% Find the Best Route in the Population
[minDist,index] = min(totalDist);
distHistory(iter) = minDist;
if minDist < globalMin
globalMin = minDist;
optRoute = pop(index,:);
if showProg
% Plot the Best Route
rte = optRoute([1:n 1]);
if dims > 2, plot3(hAx,xy(rte,1),xy(rte,2),xy(rte,3),'r.-');
else plot(hAx,xy(rte,1),xy(rte,2),'r.-'); end
title(hAx,sprintf('Total Distance = %1.4f, Iteration = %d',minDist,iter));
drawnow;
end
end
% Genetic Algorithm Operators
randomOrder = randperm(popSize);
for p = 4:4:popSize
rtes = pop(randomOrder(p-3:p),:);
dists = totalDist(randomOrder(p-3:p));
[ignore,idx] = min(dists); %#ok
bestOf4Route = rtes(idx,:);
routeInsertionPoints = sort(ceil(n*rand(1,2)));
I = routeInsertionPoints(1);
J = routeInsertionPoints(2);
for k = 1:4 % Mutate the Best to get Three New Routes
tmpPop(k,:) = bestOf4Route;
switch k
case 2 % Flip
tmpPop(k,I:J) = tmpPop(k,J:-1:I);
case 3 % Swap
tmpPop(k,[I J]) = tmpPop(k,[J I]);
case 4 % Slide
tmpPop(k,I:J) = tmpPop(k,[I+1:J I]);
otherwise % Do Nothing
end
end
newPop(p-3:p,:) = tmpPop;
end
pop = newPop;
% Update the waitbar
if showWaitbar && ~mod(iter,ceil(numIter/325))
waitbar(iter/numIter,hWait);
end
end
if showWaitbar
close(hWait);
end
if showResult
% Plots the GA Results
figure('Name','TSP_GA | Results','Numbertitle','off');
subplot(2,2,1);
pclr = ~get(0,'DefaultAxesColor');
if dims > 2, plot3(xy(:,1),xy(:,2),xy(:,3),'.','Color',pclr);
else plot(xy(:,1),xy(:,2),'.','Color',pclr); end
title('City Locations');
subplot(2,2,2);
imagesc(dmat(optRoute,optRoute));
title('Distance Matrix');
subplot(2,2,3);
rte = optRoute([1:n 1]);
if dims > 2, plot3(xy(rte,1),xy(rte,2),xy(rte,3),'r.-');
else plot(xy(rte,1),xy(rte,2),'r.-'); end
title(sprintf('Total Distance = %1.4f',minDist));
subplot(2,2,4);
plot(distHistory,'b','LineWidth',2);
title('Best Solution History');
set(gca,'XLim',[0 numIter+1],'YLim',[0 1.1*max([1 distHistory])]);
end
% Return Output
if nargout
resultStruct = struct( ...
'xy', xy, ...
'dmat', dmat, ...
'popSize', popSize, ...
'numIter', numIter, ...
'showProg', showProg, ...
'showResult', showResult, ...
'showWaitbar', showWaitbar, ...
'optRoute', optRoute, ...
'minDist', minDist);
varargout = {resultStruct};
end
end
% Subfunction to override the default configuration with user inputs
function config = get_config(defaultConfig,userConfig)
% Initialize the configuration structure as the default
config = defaultConfig;
% Extract the field names of the default configuration structure
defaultFields = fieldnames(defaultConfig);
% Extract the field names of the user configuration structure
userFields = fieldnames(userConfig);
nUserFields = length(userFields);
% Override any default configuration fields with user values
for i = 1:nUserFields
userField = userFields{i};
isField = strcmpi(defaultFields,userField);
if nnz(isField) == 1
thisField = defaultFields{isField};
config.(thisField) = userConfig.(userField);
end
end
end
خروجی حاصل از بهینهسازی مسأله فروشنده دوره‌گرد:
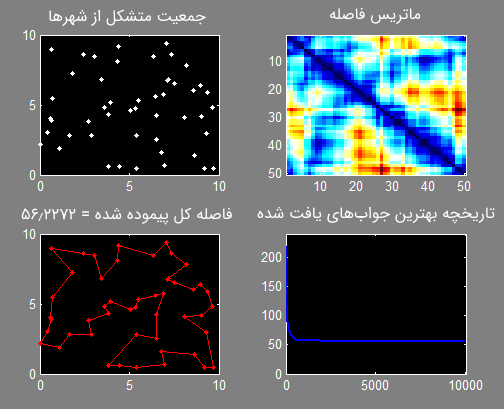
کدهای لازم برای حل مسأله فروشنده دوره‌گرد با استفاده از زبان برنامه‌نویسی پایتون:
import numpy as np, random, operator, pandas as pd, matplotlib.pyplot as plt
class City:
def __init__(self, x, y):
self.x = x
self.y = y
def distance(self, city):
xDis = abs(self.x - city.x)
yDis = abs(self.y - city.y)
distance = np.sqrt((xDis ** 2) + (yDis ** 2))
return distance
def __repr__(self):
return "(" + str(self.x) + "," + str(self.y) + ")"
class Fitness:
def __init__(self, route):
self.route = route
self.distance = 0
self.fitness= 0.0
def routeDistance(self):
if self.distance ==0:
pathDistance = 0
for i in range(0, len(self.route)):
fromCity = self.route[i]
toCity = None
if i + 1 < len(self.route):
toCity = self.route[i + 1]
else:
toCity = self.route[0]
pathDistance += fromCity.distance(toCity)
self.distance = pathDistance
return self.distance
def routeFitness(self):
if self.fitness == 0:
self.fitness = 1 / float(self.routeDistance())
return self.fitness
def createRoute(cityList):
route = random.sample(cityList, len(cityList))
return route
def initialPopulation(popSize, cityList):
population = []
for i in range(0, popSize):
population.append(createRoute(cityList))
return population
def rankRoutes(population):
fitnessResults = {}
for i in range(0,len(population)):
fitnessResults[i] = Fitness(population[i]).routeFitness()
return sorted(fitnessResults.items(), key = operator.itemgetter(1), reverse = True)
def selection(popRanked, eliteSize):
selectionResults = []
df = pd.DataFrame(np.array(popRanked), columns=["Index","Fitness"])
df['cum_sum'] = df.Fitness.cumsum()
df['cum_perc'] = 100*df.cum_sum/df.Fitness.sum()
for i in range(0, eliteSize):
selectionResults.append(popRanked[i][0])
for i in range(0, len(popRanked) - eliteSize):
pick = 100*random.random()
for i in range(0, len(popRanked)):
if pick <= df.iat[i,3]:
selectionResults.append(popRanked[i][0])
break
return selectionResults
def matingPool(population, selectionResults):
matingpool = []
for i in range(0, len(selectionResults)):
index = selectionResults[i]
matingpool.append(population[index])
return matingpool
def breed(parent1, parent2):
child = []
childP1 = []
childP2 = []
geneA = int(random.random() * len(parent1))
geneB = int(random.random() * len(parent1))
startGene = min(geneA, geneB)
endGene = max(geneA, geneB)
for i in range(startGene, endGene):
childP1.append(parent1[i])
childP2 = [item for item in parent2 if item not in childP1]
child = childP1 + childP2
return child
def breedPopulation(matingpool, eliteSize):
children = []
length = len(matingpool) - eliteSize
pool = random.sample(matingpool, len(matingpool))
for i in range(0,eliteSize):
children.append(matingpool[i])
for i in range(0, length):
child = breed(pool[i], pool[len(matingpool)-i-1])
children.append(child)
return children
def mutate(individual, mutationRate):
for swapped in range(len(individual)):
if(random.random() < mutationRate):
swapWith = int(random.random() * len(individual))
city1 = individual[swapped]
city2 = individual[swapWith]
individual[swapped] = city2
individual[swapWith] = city1
return individual
def mutatePopulation(population, mutationRate):
mutatedPop = []
for ind in range(0, len(population)):
mutatedInd = mutate(population[ind], mutationRate)
mutatedPop.append(mutatedInd)
return mutatedPop
def nextGeneration(currentGen, eliteSize, mutationRate):
popRanked = rankRoutes(currentGen)
selectionResults = selection(popRanked, eliteSize)
matingpool = matingPool(currentGen, selectionResults)
children = breedPopulation(matingpool, eliteSize)
nextGeneration = mutatePopulation(children, mutationRate)
return nextGeneration
def geneticAlgorithm(population, popSize, eliteSize, mutationRate, generations):
pop = initialPopulation(popSize, population)
print("Initial distance: " + str(1 / rankRoutes(pop)[0][1]))
for i in range(0, generations):
pop = nextGeneration(pop, eliteSize, mutationRate)
print("Final distance: " + str(1 / rankRoutes(pop)[0][1]))
bestRouteIndex = rankRoutes(pop)[0][0]
bestRoute = pop[bestRouteIndex]
return bestRoute
cityList = []
for i in range(0,25):
cityList.append(City(x=int(random.random() * 200), y=int(random.random() * 200)))
geneticAlgorithm(population=cityList, popSize=100, eliteSize=20, mutationRate=0.01, generations=500)
def geneticAlgorithmPlot(population, popSize, eliteSize, mutationRate, generations):
pop = initialPopulation(popSize, population)
progress = []
progress.append(1 / rankRoutes(pop)[0][1])
for i in range(0, generations):
pop = nextGeneration(pop, eliteSize, mutationRate)
progress.append(1 / rankRoutes(pop)[0][1])
plt.plot(progress)
plt.ylabel('Distance')
plt.xlabel('Generation')
plt.show()
geneticAlgorithmPlot(population=cityList, popSize=100, eliteSize=20, mutationRate=0.01, generations=500)
خروجی حاصل از بهینهسازی مسأله فروشنده دوره‌گرد:
از یک دیدگاه انتزاعی‌تر به الگوریتمهای محاسبات تکاملی، چنین رویکردهایی در دسته «الگوریتمهای احتمالی» (Probabilistic Algorithms) طبقه‌بندی می‌شوند. الگوریتم‌هایی نظیر «شبیه‌سازی تبرید» (Simulated Annealing)، الگوریتم بهینهسازی فاخته (Cuckoo Optimization Algorithm)، الگوریتم کلونی مورچگان (Ant Colony Optimization) و الگوریتم کرم شب تاب (Firefly Algorithm)، از جمله الگوریتمهای تکاملی محسوب می‌شوند. الگوریتم شبیه‌سازی تبرید که مدل یک فرایند طبیعی و فیزیکی را شبیه‌سازی می‌کند، ویژگی‌های مشترک زیادی با الگوریتم ژنتیک دارد:
- جواب بهینه برای یک مسأله بهینهسازی، طی یک فرایند تکراری و از طریق تغییر دادن یک یا چند جواب کاندید (Candidate Solutions) حاصل می‌شود؛ در فرایند تکراری، مقادیر متغیرهای جواب‌های کاندید تا زمانی تغییر پیدا می‌کنند که خروجی نهایی یک یا چند شرط خاص را ارضا کند.
- تغییرات حاصل شده طی فرایند تکاملی تکراری بر مبنای تصمیمات تصادفی حاصل می‌شوند.
- معمولا برای اینکه مشخص شود آیا یک جواب کاندید جدید در حال همگرایی به ناحیه حاوی جواب بهینه (و جواب بهینه یا تقریبی از آن) است، از یک تابع برازندگی استفاده می‌شود. متعاقبا در صورتی که جواب کاندید جدید در حال همگرایی به جواب بهینه مسأله یا تقریب مناسبی از آن باشد، در مراحل بعدی فرایند تکراری تکامل، مقادیر متغیرهای آن دستخوش تغییر می‌شوند.
به چنین فرایندی «تپه نوردی» (Hill Climbing) در فضای جستجوی مسأله نیز گفته می‌شود. با این حال، از آنجایی که معمولا معیار دقیقی برای مشخص کردن میزان نزدیکی یا همگرایی یک جواب کاندید به جواب بهینه وجود ندارد و فرایند تکامل در الگوریتمهای محاسبات تکاملی یک فرایند تصادفی است، یک جواب کاندید با برازندگی کمتر (جواب کاندیدی که همگرایی کمی با جواب بهینه دارد) نیز می‌تواند در فرایند تکامل شرکت کند و مقادیر متغیرهای آن دستخوش تغییر شود؛ البته، جواب‌های کاندیدی که برازندگی کمتری نسبت به دیگر جواب‌ها دارند، با احتمال کمتری نسبت به جواب‌های کاندید برازنده‌تر، می‌توانند در فرایند تکامل شرکت کنند.
اگر چه در تئوری نشان داده شده است که «استراتژی‌های تکاملی» (Evolutionary Strategies) را می‌توان در دامنه وسیعی از مسائل بهینهسازی مورد استفاده قرار داد، ولی به‌کارگیری آن‌ها به صورت عملی و در مسائل جهان واقعی نشان داد که استفاده از الگوریتمهای محاسبات تکاملی در مسائل خاص، نیازمند ایجاد تغییرات در فرایند تکاملی تعبیه شده است تا جواب‌های حاصل از کیفیت مناسبی برخوردار باشند.
دسته‌بندی الگوریتمهای محاسبات تکاملی
در یک دسته‌بندی جامع و کلی‌تر، الگوریتمهای محاسبات تکاملی در روش‌های «هوش محاسباتی» (Computational Intelligence) یا «محاسبات نرم» (Soft Computing) طبقه‌بندی می‌شوند. دسته‌بندی کلی الگوریتمهای هوش محاسباتی در ادامه نمایش داده شده است:
- روش‌های «هوش محاسباتی» (Computational Intelligence) یا «محاسبات نرم» (Soft Computing)
- «شبکه‌های عصبی مصنوعی» (Artificial Neural Network)
- «سیستم‌های فازی» (Fuzzy Systems)
- محاسبات تکاملی (Evolutionary Computation) یا الگوریتمهای تکاملی (Evolutionary Algorithms)
- روش «برنامه‌نویسی تکاملی» (Evolutionary programming)
- روش «استراتژی‌های تکاملی» (Evolutionary Strategies)
- روش «الگوریتم ژنتیک» (Genetic Algorithm)
- روش «برنامه‌نویسی ژنتیک» (Genetic Programming)
- و دیگر الگوریتمهای محاسبات تکاملی
انواع تکنیک‌های محاسبات تکاملی
تفاوت میان تکنیک‌های مختلفی محاسبات تکاملی، در نحوه «نمایش کدبندی جواب‌های کاندید» (Representation of Candidate Solutions Representation)، جزئیات مرتبط با پیادهسازی این دسته از الگوریتم‌ها و ذات مسأله بهینهسازی مورد نظر است. در ادامه، به طور مختصر با مهم‌ترین انواع الگوریتمهای محاسبات تکاملی آشنا خواهید شد:
- الگوریتم ژنتیک: یکی از محبوب‌ترین انواع الگوریتمهای محاسبات تکاملی محسوب می‌شود. در الگوریتم ژنتیک، جواب‌های کاندید به فرم رشته (معمولا رشته‌های باینری) کدبندی و نمایش داده می‌شوند. با اعمال عملگرهای تکاملی نظیر ترکیب و جهش، جمعیت جواب‌های کاندید به سمت جواب بهینه همگرا می‌شوند. از الگوریتم ژنتیک بیشتر در مسائل بهینهسازی استفاده می‌شود.
پیادهسازی الگوریتم ژنتیک در زبان متلب: در ادامه، کدهای پیادهسازی الگوریتم ژنتیک برای مدل‌سازی و حل «الگوریتم راسو» (Weasel algorithm) [+] نمایش داده شده است. هدف این الگوریتم این است که نشان دهد تغییرات تصادفی در ژنها و ترکیب آن‌ها با یک مکانیزم انتخاب غیر تصادفی، منجر به تولید نتایجی متفاوت و بهتر از شانس خالص در فرایندهای تکاملی خواهد شد. مشخصات این مسأله به شکل زیر است:
- جمعیت اولیه: یک آرایه 28 عنصری متشکل از الفبای ABCDEFGHIJKLMNOPQRSTUVWXYZ.
- هدف نهایی: تبدیل رشته ورودی یا جمعیت اولیه به رشته METHINKS IT IS LIKE A WEASEL.
- تابع برازندگی: تابعی که شباهت آرگومان ورودی را به رشته نهایی یا هدف نهایی مشخص می‌کند.
- عملگرهای تکاملی (پیادهسازی عملگر انتخاب و جهش ضروری است، ولی پیادهسازی عملگر ترکیب اختیاری است)
%This class impliments a string that mutates to a target
classdef EvolutionaryAlgorithm
properties
target;
parent;
children = {};
validAlphabet;
%Constants
numChildrenPerIteration;
maxIterations;
mutationRate;
end
methods
%Class constructor
function family = EvolutionaryAlgorithm(target,mutationRate,numChildren,maxIterations)
family.validAlphabet = char([32 (65:90)]); %Space char and A-Z
family.target = target;
family.children = cell(numChildren,1);
family.numChildrenPerIteration = numChildren;
family.maxIterations = maxIterations;
family.mutationRate = mutationRate;
initialize(family);
end %class constructor
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Helper functions and class get/set functions
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%setAlphabet() - sets the valid alphabet for the current instance
%of the EvolutionaryAlgorithm class.
function setAlphabet(family,alphabet)
if(ischar(alphabet))
family.validAlphabet = alphabet;
%Makes change permanent
assignin('caller',inputname(1),family);
else
error 'New alphabet must be a string or character array';
end
end
%setTarget() - sets the target for the current instance
%of the EvolutionaryAlgorithm class.
function setTarget(family,target)
if(ischar(target))
family.target = target;
%Makes change permanent
assignin('caller',inputname(1),family);
else
error 'New target must be a string or character array';
end
end
%setMutationRate() - sets the mutation rate for the current instance
%of the EvolutionaryAlgorithm class.
function setMutationRate(family,mutationRate)
if(isnumeric(mutationRate))
family.mutationRate = mutationRate;
%Makes change permanent
assignin('caller',inputname(1),family);
else
error 'New mutation rate must be a double precision number';
end
end
%setMaxIterations() - sets the maximum number of iterations during
%evolution for the current instance of the EvolutionaryAlgorithm class.
function setMaxIterations(family,maxIterations)
if(isnumeric(maxIterations))
family.maxIterations = maxIterations;
%Makes change permanent
assignin('caller',inputname(1),family);
else
error 'New maximum amount of iterations must be a double precision number';
end
end
%display() - overrides the built-in MATLAB display() function, to
%display the important class variables
function display(family)
disp([sprintf('Target: %s\n',family.target)...
sprintf('Parent: %s\n',family.parent)...
sprintf('Valid Alphabet: %s\n',family.validAlphabet)...
sprintf('Number of Children: %d\n',family.numChildrenPerIteration)...
sprintf('Mutation Rate [0,1]: %d\n',family.mutationRate)...
sprintf('Maximum Iterations: %d\n',family.maxIterations)]);
end
%disp() - overrides the built-in MATLAB disp() function, to
%display the important class variables
function disp(family)
display(family);
end
%randAlphabetElement() - Generates a random character from the
%valid alphabet for the current instance of the class.
function elements = randAlphabetElements(family,numChars)
%Sample the valid alphabet randomly from the uniform
%distribution
N = length(family.validAlphabet);
choices = ceil(N*rand(1,numChars));
elements = family.validAlphabet(choices);
end
%initialize() - Sets the parent to a random string of length equal
%to the length of the target
function parent = initialize(family)
family.parent = randAlphabetElements(family,length(family.target));
parent = family.parent;
%Makes changes to the instance of EvolutionaryAlgorithm permanent
assignin('caller',inputname(1),family);
end %initialize
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Functions required by task specification
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%mutate() - generates children from the parent and mutates them
function mutate(family)
sizeParent = length(family.parent);
%Generate mutatant children sequentially
for child = (1:family.numChildrenPerIteration)
parentCopy = family.parent;
for charIndex = (1:sizeParent)
if (rand(1) < family.mutationRate)
parentCopy(charIndex) = randAlphabetElements(family,1);
end
end
family.children{child} = parentCopy;
end
%Makes changes to the instance of EvolutionaryAlgorithm permanent
assignin('caller',inputname(1),family);
end %mutate
%fitness() - Computes the Hamming distance between the target
%string and the string input as the familyMember argument
function theFitness = fitness(family,familyMember)
if not(ischar(familyMember))
error 'The second argument must be a string';
end
theFitness = sum(family.target == familyMember);
end
%evolve() - evolves the family until the target is reached or it
%exceeds the maximum amount of iterations
function [iteration,mostFitFitness] = evolve(family)
iteration = 0;
mostFitFitness = 0;
targetFitness = fitness(family,family.target);
disp(['Target fitness is ' num2str(targetFitness)]);
while (mostFitFitness < targetFitness) && (iteration < family.maxIterations)
iteration = iteration + 1;
mutate(family);
parentFitness = fitness(family,family.parent);
mostFit = family.parent;
mostFitFitness = parentFitness;
for child = (1:family.numChildrenPerIteration)
childFitness = fitness(family,family.children{child});
if childFitness > mostFitFitness
mostFit = family.children{child};
mostFitFitness = childFitness;
end
end
family.parent = mostFit;
disp([num2str(iteration) ': ' mostFit ' - Fitness: ' num2str(mostFitFitness)]);
end
%Makes changes to the instance of EvolutionaryAlgorithm permanent
assignin('caller',inputname(1),family);
end %evolve
end %methods
end %classdef
اجرا:
>> instance = EvolutionaryAlgorithm('METHINKS IT IS LIKE A WEASEL',.08,50,1000)
Target: METHINKS IT IS LIKE A WEASEL
Parent: UVEOCXXFBGDCSFNMJQNWTPJ PCVA
Valid Alphabet: ABCDEFGHIJKLMNOPQRSTUVWXYZ
Number of Children: 50
Mutation Rate [0,1]: 8.000000e-002
Maximum Iterations: 1000
>> evolve(instance);
پیادهسازی الگوریتم ژنتیک در زبان پایتون:
from string import letters
from random import choice, random
target = list("METHINKS IT IS LIKE A WEASEL")
charset = letters + ' '
parent = [choice(charset) for _ in range(len(target))]
minmutaterate = .09
C = range(100)
perfectfitness = float(len(target))
def fitness(trial):
'Sum of matching chars by position'
return sum(t==h for t,h in zip(trial, target))
def mutaterate():
'Less mutation the closer the fit of the parent'
return 1-((perfectfitness - fitness(parent)) / perfectfitness * (1 - minmutaterate))
def mutate(parent, rate):
return [(ch if random() <= rate else choice(charset)) for ch in parent]
def que():
'(from the favourite saying of Manuel in Fawlty Towers)'
print ("#%-4i, fitness: %4.1f%%, '%s'" %
(iterations, fitness(parent)*100./perfectfitness, ''.join(parent)))
def mate(a, b):
place = 0
if choice(xrange(10)) < 7:
place = choice(xrange(len(target)))
else:
return a, b
return a, b, a[:place] + b[place:], b[:place] + a[place:]
iterations = 0
center = len(C)/2
while parent != target:
rate = mutaterate()
iterations += 1
if iterations % 100 == 0: que()
copies = [ mutate(parent, rate) for _ in C ] + [parent]
parent1 = max(copies[:center], key=fitness)
parent2 = max(copies[center:], key=fitness)
parent = max(mate(parent1, parent2), key=fitness)
que()
- «برنامه‌نویسی ژنتیک» (Genetic Programming): در این روش محاسبات تکاملی، جواب‌ها به فرم برنامه‌های کامپیوتری و معمولا در قالب درخت LISP نمایش داده می‌شوند. همچنین، برازندگی جواب‌های کاندید به وسیله قابلیت آن‌ها در حل یک مسأله محاسباتی سنجیده می‌شود.
پیادهسازی برنامه‌نویسی ژنتیک در زبان پایتون:
from random import random, randint, seed
from statistics import mean
from copy import deepcopy
import matplotlib.pyplot as plt
from IPython.display import Image, display
from graphviz import Digraph, Source
POP_SIZE = 60 # population size
MIN_DEPTH = 2 # minimal initial random tree depth
MAX_DEPTH = 5 # maximal initial random tree depth
GENERATIONS = 250 # maximal number of generations to run evolution
TOURNAMENT_SIZE = 5 # size of tournament for tournament selection
XO_RATE = 0.8 # crossover rate
PROB_MUTATION = 0.2 # per-node mutation probability
BLOAT_CONTROL = False # True adds bloat control to fitness function
def add(x, y): return x + y
def sub(x, y): return x - y
def mul(x, y): return x * y
FUNCTIONS = [add, sub, mul]
TERMINALS = ['x', -2, -1, 0, 1, 2]
def target_func(x): # evolution's target
return x*x*x*x + x*x*x + x*x + x + 1
def generate_dataset(): # generate 101 data points from target_func
dataset = []
for x in range(-100,101,2):
x /= 100
dataset.append([x, target_func(x)])
return dataset
class GPTree:
def __init__(self, data = None, left = None, right = None):
self.data = data
self.left = left
self.right = right
def node_label(self): # return string label
if (self.data in FUNCTIONS):
return self.data.__name__
else:
return str(self.data)
def draw(self, dot, count): # dot & count are lists in order to pass "by reference"
node_name = str(count[0])
dot[0].node(node_name, self.node_label())
if self.left:
count[0] += 1
dot[0].edge(node_name, str(count[0]))
self.left.draw(dot, count)
if self.right:
count[0] += 1
dot[0].edge(node_name, str(count[0]))
self.right.draw(dot, count)
def draw_tree(self, fname, footer):
dot = [Digraph()]
dot[0].attr(kw='graph', label = footer)
count = [0]
self.draw(dot, count)
Source(dot[0], filename = fname + ".gv", format="png").render()
display(Image(filename = fname + ".gv.png"))
def compute_tree(self, x):
if (self.data in FUNCTIONS):
return self.data(self.left.compute_tree(x), self.right.compute_tree(x))
elif self.data == 'x': return x
else: return self.data
def random_tree(self, grow, max_depth, depth = 0): # create random tree using either grow or full method
if depth < MIN_DEPTH or (depth < max_depth and not grow):
self.data = FUNCTIONS[randint(0, len(FUNCTIONS)-1)]
elif depth >= max_depth:
self.data = TERMINALS[randint(0, len(TERMINALS)-1)]
else: # intermediate depth, grow
if random () > 0.5:
self.data = TERMINALS[randint(0, len(TERMINALS)-1)]
else:
self.data = FUNCTIONS[randint(0, len(FUNCTIONS)-1)]
if self.data in FUNCTIONS:
self.left = GPTree()
self.left.random_tree(grow, max_depth, depth = depth + 1)
self.right = GPTree()
self.right.random_tree(grow, max_depth, depth = depth + 1)
def mutation(self):
if random() < PROB_MUTATION: # mutate at this node
self.random_tree(grow = True, max_depth = 2)
elif self.left: self.left.mutation()
elif self.right: self.right.mutation()
def size(self): # tree size in nodes
if self.data in TERMINALS: return 1
l = self.left.size() if self.left else 0
r = self.right.size() if self.right else 0
return 1 + l + r
def build_subtree(self): # count is list in order to pass "by reference"
t = GPTree()
t.data = self.data
if self.left: t.left = self.left.build_subtree()
if self.right: t.right = self.right.build_subtree()
return t
def scan_tree(self, count, second): # note: count is list, so it's passed "by reference"
count[0] -= 1
if count[0] <= 1:
if not second: # return subtree rooted here
return self.build_subtree()
else: # glue subtree here
self.data = second.data
self.left = second.left
self.right = second.right
else:
ret = None
if self.left and count[0] > 1: ret = self.left.scan_tree(count, second)
if self.right and count[0] > 1: ret = self.right.scan_tree(count, second)
return ret
def crossover(self, other): # xo 2 trees at random nodes
if random() < XO_RATE:
second = other.scan_tree([randint(1, other.size())], None) # 2nd random subtree
self.scan_tree([randint(1, self.size())], second) # 2nd subtree "glued" inside 1st tree
# end class GPTree
def init_population(): # ramped half-and-half
pop = []
for md in range(3, MAX_DEPTH + 1):
for i in range(int(POP_SIZE/6)):
t = GPTree()
t.random_tree(grow = True, max_depth = md) # grow
pop.append(t)
for i in range(int(POP_SIZE/6)):
t = GPTree()
t.random_tree(grow = False, max_depth = md) # full
pop.append(t)
return pop
def error(individual, dataset):
return mean([abs(individual.compute_tree(ds[0]) - ds[1]) for ds in dataset])
def fitness(individual, dataset):
if BLOAT_CONTROL:
return 1 / (1 + error(individual, dataset) + 0.01*individual.size())
else:
return 1 / (1 + error(individual, dataset))
def selection(population, fitnesses): # select one individual using tournament selection
tournament = [randint(0, len(population)-1) for i in range(TOURNAMENT_SIZE)] # select tournament contenders
tournament_fitnesses = [fitnesses[tournament[i]] for i in range(TOURNAMENT_SIZE)]
return deepcopy(population[tournament[tournament_fitnesses.index(max(tournament_fitnesses))]])
def prepare_plots():
fig, axarr = plt.subplots(2, sharex=True)
fig.canvas.set_window_title('EVOLUTIONARY PROGRESS')
fig.subplots_adjust(hspace = 0.5)
axarr[0].set_title('error', fontsize=14)
axarr[1].set_title('mean size', fontsize=14)
plt.xlabel('generation', fontsize=18)
plt.ion() # interactive mode for plot
axarr[0].set_xlim(0, GENERATIONS)
axarr[0].set_ylim(0, 1) # fitness range
xdata = []
ydata = [ [], [] ]
line = [None, None]
line[0], = axarr[0].plot(xdata, ydata[0], 'b-') # 'b-' = blue line
line[1], = axarr[1].plot(xdata, ydata[1], 'r-') # 'r-' = red line
return axarr, line, xdata, ydata
def plot(axarr, line, xdata, ydata, gen, pop, errors, max_mean_size):
xdata.append(gen)
ydata[0].append(min(errors))
line[0].set_xdata(xdata)
line[0].set_ydata(ydata[0])
sizes = [ind.size() for ind in pop]
if mean(sizes) > max_mean_size[0]:
max_mean_size[0] = mean(sizes)
axarr[1].set_ylim(0, max_mean_size[0])
ydata[1].append(mean(sizes))
line[1].set_xdata(xdata)
line[1].set_ydata(ydata[1])
plt.draw()
plt.pause(0.01)
def main():
# init stuff
seed() # init internal state of random number generator
dataset = generate_dataset()
population= init_population()
best_of_run = None
best_of_run_error = 1e20
best_of_run_gen = 0
fitnesses = [fitness(ind, dataset) for ind in population]
max_mean_size = [0] # track maximal mean size for plotting
axarr, line, xdata, ydata = prepare_plots()
# go evolution!
for gen in range(GENERATIONS):
nextgen_population=[]
for i in range(POP_SIZE):
parent1 = selection(population, fitnesses)
parent2 = selection(population, fitnesses)
parent1.crossover(parent2)
parent1.mutation()
nextgen_population.append(parent1)
population=nextgen_population
fitnesses = [fitness(ind, dataset) for ind in population]
errors = [error(ind, dataset) for ind in population]
if min(errors) < best_of_run_error:
best_of_run_error = min(errors)
best_of_run_gen = gen
best_of_run = deepcopy(population[errors.index(min(errors))])
print("________________________")
best_of_run.draw_tree("best_of_run",\
"gen: " + str(gen) + ", error: " + str(round(best_of_run_error,3)))
plot(axarr, line, xdata, ydata, gen, population, errors, max_mean_size)
if best_of_run_error <= 1e-5: break
endrun = "_________________________________________________\nEND OF RUN (bloat control was "
endrun += "ON)" if BLOAT_CONTROL else "OFF)"
print(endrun)
s = "\n\nbest_of_run attained at gen " + str(best_of_run_gen) + " and has error=" + str(round(best_of_run_error,3))
best_of_run.draw_tree("best_of_run",s)
if __name__== "__main__":
main()
- برنامه‌نویسی تکاملی (Evolutionary Programming): مشابه برنامه‌نویسی ژنتیک است، با این تفاوت که ساختار برنامه‌های کامپیوتری ثابت است و پارامترهای عددی این الگوریتم را می‌توان در فرایند تکامل بهینه کرد.
- برنامه‌نویسی عبارات ژنی (Gene expression programming): همانند برنامه‌نویسی ژنتیک، الگوریتم برنامه‌نویسی عبارات ژنی نیز برای تکامل برنامه‌های کامپیوتری مورد استفاده قرار می‌گیرند. با این تفاوت که در این الگوریتم، یک سیستم ژنوتایپ-فنوتیپ (Genotype-Phenotype) مورد بررسی قرار می‌گیرد که در آن برنامه‌های کامپیوتری با اندازه مختلف، در کروموزم‌های خطی با اندازه ثابت کد بندی شدهاند.
- استراتژی تکاملی (Evolution strategy): در این روش، از بردارهای متشکل از مقادیر حقیقی برای نمایش جواب‌های کاندید استفاده می‌شود. همچنین، این دسته از الگوریتمهای محاسبات تکاملی از نرخ جهش خود تطبیقی (Self-adaptive Mutation Rate) استفاده می‌کنند.
پیادهسازی استراتژی تکاملی طبیعی در زبان پایتون:
"""
The basic idea about Nature Evolution Strategy with visualation.
Visit my tutorial website for more: https://morvanzhou.github.io/tutorials/
Dependencies:
Tensorflow >= r1.2
numpy
matplotlib
"""
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.contrib.distributions import MultivariateNormalFullCovariance
DNA_SIZE = 2 # parameter (solution) number
N_POP = 20 # population size
N_GENERATION = 100 # training step
LR = 0.02 # learning rate
# fitness function
def get_fitness(pred): return -((pred[:, 0])**2 + pred[:, 1]**2)
# build multivariate distribution
mean = tf.Variable(tf.random_normal([2, ], 13., 1.), dtype=tf.float32)
cov = tf.Variable(5. * tf.eye(DNA_SIZE), dtype=tf.float32)
mvn = MultivariateNormalFullCovariance(loc=mean, covariance_matrix=cov)
make_kid = mvn.sample(N_POP) # sampling operation
# compute gradient and update mean and covariance matrix from sample and fitness
tfkids_fit = tf.placeholder(tf.float32, [N_POP, ])
tfkids = tf.placeholder(tf.float32, [N_POP, DNA_SIZE])
loss = -tf.reduce_mean(mvn.log_prob(tfkids)*tfkids_fit) # log prob * fitness
train_op = tf.train.GradientDescentOptimizer(LR).minimize(loss) # compute and apply gradients for mean and cov
sess = tf.Session()
sess.run(tf.global_variables_initializer()) # initialize tf variables
# something about plotting (can be ignored)
n = 300
x = np.linspace(-20, 20, n)
X, Y = np.meshgrid(x, x)
Z = np.zeros_like(X)
for i in range(n):
for j in range(n):
Z[i, j] = get_fitness(np.array([[x[i], x[j]]]))
plt.contourf(X, Y, -Z, 100, cmap=plt.cm.rainbow); plt.ylim(-20, 20); plt.xlim(-20, 20); plt.ion()
# training
for g in range(N_GENERATION):
kids = sess.run(make_kid)
kids_fit = get_fitness(kids)
sess.run(train_op, {tfkids_fit: kids_fit, tfkids: kids}) # update distribution parameters
# plotting update
if 'sca' in globals(): sca.remove()
sca = plt.scatter(kids[:, 0], kids[:, 1], s=30, c='k');plt.pause(0.01)
print('Finished'); plt.ioff(); plt.show()
- «تکامل تفاضلی» (Differential Evolution): این الگوریتم بر مبنای تفاوت میان بردارها بنا نهاده شده است. بنابراین بیشتر برای مسائل «بهینهسازی عددی» (Numerical Optimization) مناسب خواهد بود.
- «تکامل عصبی» (Neuroevolution): مشابه الگوریتم برنامه‌نویسی ژنتیک است. این دسته از الگوریتمهای محاسبات تکاملی فرمی از هوش مصنوعی هستند که از الگوریتمهای تکاملی برای تولید شبکه‌های عصبی مصنوعی (Artificial Neural Network)، قوانین، توپولوژی شبکه و پارامترها استفاده می‌کنند.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزشهای الگوریتمهای بهینهسازی هوشمند
- آموزش تئوری و عملی الگوریتمهای ژنتیک
- مجموعه آموزشهای هوش مصنوعی
- الگوریتم بهینه سازی فاخته — از صفر تا صد
- الگوریتم ژنتیک — از صفر تا صد
- الگوریتم کلونی مورچگان — از صفر تا صد
- الگوریتم کرم شب تاب — از صفر تا صد
^^
سلام
رفرنس این مطالب را هم ذکر بفرمایید.
ممنون
سلام، وقت شما بخیر؛
منبع تمامی مطالب مجله فرادرس در انتهای آن‌ها و پس از بخش معرفی آموزش‌ها و مطالب مشابه ذکر شدهاند.
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.