الگوریتم کلونی مورچگان – از صفر تا صد

الگوریتم کلونی مورچگان یا در حقیقت «بهینه‌سازی کلونی مورچگان» (Ant Colony Optimization) همانطور که از نام آن مشخص است، بر پایه رفتار طبیعی کلونی‌های مورچگان و مورچگان کارگر شاغل در آن‌ها بنا نهاده شده است. فرآیند یافتن منابع غذایی در کلونی مورچگان بسیار بهینه است. زمانی که مورچه‌ها عملیات کاوش برای یافتن منابع غذایی را آغاز می‌کنند، به طور طبیعی یک مسیر «منطقی» و «بهینه» از آشیانه خود به منابع غذایی پیدا می‌کنند. به عبارت دیگر، جمعیت مورچگان به نحوی همیشه قادر هستند تا یک مسیر بهینه را برای تامین منابع غذایی مورد نیاز بیابند. شبیه‌سازی چنین رفتار بهینه‌ای، پایه و اساس بهینه سازی کلونی مورچگان را تشکیل می‌دهد. در این مطلب، الگوریتم کلونی مورچگان به طور کامل تشریح شده است. باید توجه داشت که نام دقیق این الگوریتم، بهینه سازی کلونی مورچگان است که توسط اغلب افراد به آن الگوریتم مورچگان یا الگوریتم کلونی مورچگان گفته می‌شود.

دو مورچه را فرض کنید که در حال حرکت از آشیانه به منبع غذایی، از طریق دو مسیر کاملا متفاوت از هم هستند. مورچه‌ها در ضمن حرکت خود به سمت منبع غذایی، ردی از «فرومون» (Pheromone) در محیط منتشر می‌کنند که به‌طور طبیعی و با گذر زمان متلاشی می‌شود. مورچه‌ای که (به‌طور تصادفی) کوتاهترین مسیر به سمت منبع غذایی را انتخاب کرده، سفر برگشتی به سمت آشیانه را زودتر از دیگر مورچه‌ها آغاز می‌کند. در چنین حالتی، این مورچه در مسیر بازگشت به آشیانه، دوباره شروع به منتشر کردن فرومون در محیط می‌کند و از این طریق، رد فرومون به جا گذاشته در کوتاهترین مسیر را تقویت می‌کند.

مورچه‌های دیگر، به‌طور غریزی، قوی‌ترین مسیر فرومون موجود در محیط را دنبال و رد فرومون در این مسیر را تقویت می‌کنند. پس از گذشت مدت زمان مشخصی، نه تنها رد فرومون موجود در کوتاه‌ترین مسیر متلاشی نمی‌شود، بلکه، با انباشته شدن رد فرومون دیگر مورچه‌ها، بیش از پیش تقویت می‌شود. مسیری که قوی‌ترین رد فرومون در آن به جا گذاشته شده باشد، به مسیر پیش فرض برای حرکت مورچه‌ها از کلونی به منبع غذایی و برعکس تبدیل می‌شود.

روش بهینه‌سازی کلونی مورچگان، مدلی برای پیاده‌سازی روش‌های بهینه‌سازی ارائه می‌دهد. تاکنون، پیاده‌سازی‌های موفق متفاوتی از این روش بهینه‌سازی ارائه شده است. الگوریتم‌هایی نظیر «سیستم مورچگان» (َAnt System)، «سیستم کلونی مورچگان» (Ant Colony System) و «سیستم مورچگان Min-Max» از جمله مهم‌ترین و موفق‌ترین پیاده‌سازی‌های صورت گرفته از این روش بهینه‌سازی محسوب می‌شوند.

مقدمه‌ای بر الگوریتم کلونی مورچگان

در این مطب سعی بر آن است تا ویژگی‌ها و مراحل پیاده‌سازی روش الگوریتم کلونی مورچگان شرح داده شود؛ روشی «فرا اکتشافی» (Metaheuristic) که از رفتار بهینه مورچه‌ها الهام گرفته شده است. الگوریتم مورچگان، روشی بسیار قدرتمند برای حل «مسائل بهینه‌سازی ترکیبیاتی» (Combinatorial Optimization Problems) محسوب می‌شود.

الگوریتم‌های مشتق شده از الگوریتم کلونی مورچگان، زیر مجموعه‌ای از روش‌های «هوش ازدحامی» (Swarm Intelligence) هستند. این دسته روش‌ها، حوزه تحقیقاتی و مطالعاتی به شمار می‌آیند که به مطالعه الگوریتم‌های الهام گرفته شده از مفهوم «رفتارهای ازدحامی» (Swarm Behaviors) می‌پردازند. الگوریتم‌های هوش ازدحامی از مجموعه‌ای از موجودیت‌های فردی ساده تشکیل شده‌اند که از طریق «خودسازماندهی» (Self-Organizing) با یکدیگر تعامل و همکاری می‌کنند. منظور از خودسازماندهی، نبود سیستم کنترل مرکزی برای کنترل و ایجاد هماهنگی میان اعضای یک سیستم هوش ازدحامی است.

پیش از ادامه این مبحث لازم است یادآور شویم که می‌توانید هوش جمعی را با استفاده از مجموعه آموزش هوش ازدحامی فرادرس یاد بگیرید.

گذار از ویژگی‌های زیستی به الگوریتم‌های کامپیوتری

پیش از آنکه الگوریتم کلونی مورچگان مورد بررسی قرار داده شود، لازم است برخی از مفاهیم مرتبط با فرآیندهای زیستی موجود در مورچه‌ها مطالعه شود؛ مفاهیمی که سبب درک بهتر خواننده از رفتارهای بهینه این موجود در هنگام تعامل با محیط می‌شوند. در ابتدا، برخی از مشاهدات به دست آمده از مطالعه رفتار مورچه‌ها در طبیعت مورد بررسی قرار داده می‌شود.

در ادامه نشان داده خواهد شد که این مشاهدات چگونه الهام‌بخش تولید الگوریتم کلونی مورچگان شده‌اند.

رفتار مورچگان

حشره‌شناس فرانسوی، پیر پائول گراس (Pierre-Paul Grassé) اولین محققی بود که رفتار اجتماعی حشرات را مورد بررسی قرار داد. ایشان در بازه سال‌های اولیه دهه 40 میلادی تا اواخر دهه 50 میلادی، به مطالعه و تحقیق در مورد رفتار «موریانه‌ها» (Termites) پرداخت. در جریان این مطالعات، او به این موضوع پی برد که این گونه حشره‌ای می‌تواند به سیگنال‌های «محرک‌» (Stimuli) محیطی واکنش نشان دهد. چنین محرک‌هایی، به نوبه خود، نوعی واکنش برنامه‌نویسی شده ژنتیکی در این موجودات را فعال می‌کند.

این دانشمند، پی برد که تاثیرات این واکنش‌های ژنتیکی (از سوی موریانه) نه تنها می‌تواند به عنوان محرکی جدید برای خود موریانه عمل کند (ایجاد واکنش‌های متعاقب دیگر در پاسخ به محرک‌های محیطی)، بلکه دیگر موریانه‌های موجود در کلونی را نیز تحت تاثیر قرار می‌دهد و واکنش‌های خاصی را در آن‌‌ها برمی‌انگیزد. ایشان از اصطلاح «نشانه‌ورزی» (Stigmergy) برای توصیف این نوع ارتباط غیر مستقیم میان موریانه‌ها استفاده کرد. در این ارتباط کد شده ژنتیکی، گونه‌های کارگری حشرات از طریق عملکرد حاصل از تعامل با محیط تحریک می‌شوند و واکنش‌های ژنتیکی خاصی از خود نشان می‌دهند.

این دسته از ارتباطات ژنتیکی و غیر مستقیم میان حشرات، از دو جهت با دیگر وسایل ارتباطی متفاوت است:

• طبیعتِ فیزیکی و غیر نمادین اطلاعات مبادله شده میان حشرات: این اطلاعات، مترادف با تغییرات حالات محیطی-فیزیکی است که در اثر تعامل حشره با محیط صورت می‌پذیرد.
• طبیعتِ (ذات) محلی اطلاعات مبادله شده: این دسته از اطلاعات تنها توسط حشراتی قابل دسترسی است که از محیط حاوی این اطلاعات بازدید کرده باشند یا در همسایگی بلافاصل این محیط قرار گرفته باشند. به عبارت دیگر، چنین اطلاعاتی توسط تمامی حشرات موجود در کلونی قابل دریافت نیست و یک فاکتور جغرافیایی در تبادل اطلاعات میان حشرات مؤثر است.

نمونه‌هایی از چنین ارتباطات غیر مستقیمی در کلونی مورچگان نیز قابل مشاهده است. در بسیاری از گونه‌های مورچگان، زمانی که مورچه‌ها از کلونی خود به سمت منابع غذایی حرکت می‌کنند، ماده‌ای را روی زمین منتشر می‌کنند که به آن فرومون گفته می‌شود. مورچه‌های دیگر قادر هستند تا فرومون منتشر شده در محیط را ببویند. وجود فرمون در محیط، مسیر انتخابی توسط مورچگان را تحت تاثیر قرار می‌دهد. به عبارت دیگر، مورچه‌ها معمولا تمایل دارند مسیر حاوی فرومون غلیظ‌تر را دنبال کنند. فرومون منتشر شده، سبب ایجاد «رد فرومون» (Pheromone Trail) در محیط می‌شود. رد فرومون به مورچه‌ها این امکان را می‌دهد که بتوانند منابع غذایی مناسبی که پیش از این توسط دیگر مورچه شناسایی شده را پیدا کنند.

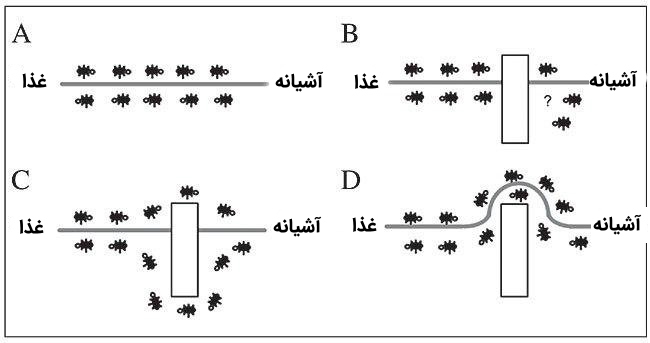
در آزمایش جالبی که برای مطالعه بهتر این ویژگی مورچه‌ها طراحی شده بود، دانشمندان میان کلونی مورچگان و منابع غذایی، دو پل با طول‌های متفاوت قرار دادند. در ابتدا، جمعیت مورچه‌ها شروع به جستجو در محیط برای یافتن منابع غذایی کردند. مورچه‌هایی که به طور کاملا تصادفی مسیر کوتاه‌تر را انتخاب کرده بودند، سریع‌تر به منابع غذایی رسیدند. این دسته از مورچه‌ها، مسیر بازگشت به کلونی را سریع‌تر و در زمان کمتری پیمودند. در نتیجه، رد فرومون منتشر شده در مسیر کوتاه‌تر تقویت شد. از آن‌جا که مورچه‌ها مسیر حاوی فرومون با غلظت بیشتر را ترجیح می‌دهند، پس از مدت زمان خاصی جمعیت مورچگان، مسیر کوتاه‌تر را با احتمال بیشتری انتخاب می‌کردند. بنابراین، به کمک مکانیزم منتشر کردن و دنبال کرد رد فرومون در محیط، مورچه‌ها به سرعت به مسیر کوتاه‌تر همگرا شدند.

این آزمایش نتایج بسیار شگفت انگیزی برای محققان به ارمغان آورد. آن‌ها کشف کردند که مورچه‌ها از رفتار بهینه ازدحامی مبتنی بر «بازخورد مثبت» (Positive Feedback) برای یافتن کوتاه‌ترین مسیر از کلونی به منابع غذایی استفاده می‌کنند. به چنین مکانیزمی، «خودکاتالیز» یا «اتوکاتالیز» (Autocatalysis) نیز گفته می‌شود. در ادامه، توضیح داده خواهد شد که مطالعات انجام شده روی جمعیت مورچه‌ها، چگونه منجر به توسعه الگوریتم‌های بهینه‌سازی می‌شود. به‌عبارت دیگر، یک الگوریتم بهینه‌سازی الهام گرفته شده از رفتار بهینه مورچگان، باید چه ویژگی‌هایی داشته باشد.

ویژگی‌های یک الگوریتم بهینه‌سازی الهام گرفته شده از رفتار بهینه مورچگان

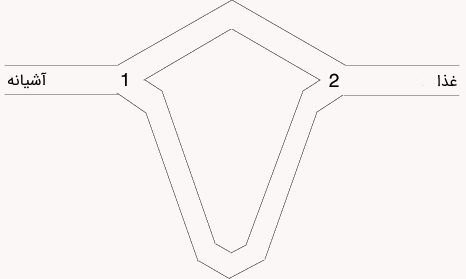
محققان، در پی مشاهده نتایج آزمایش «پل باینری» (Binary Bridge Experiment)، در صدد آن برآمدند تا مدلی ریاضی را برای توصیف رفتار بهینه مورچگان توسعه دهند.

با فرض اینکه پس از گذشتن $$t$$ واحد زمانی از زمان آغاز آزمایش، $$m_{1}$$ مورچه از پل اول و $$m_{2}$$ مورچه از پل دوم استفاده کرده باشند، احتمال ($$p_{1}$$) اینکه مورچه $$m+1$$ پل اول را انتخاب کند برابر است با:

$$p_{1} (m+1)=\frac{(m_{1} + k)^{h}}{({(m_{1} + k)^{h}}+ {(m_{2} + k)^{h}})}$$

در این رابطه، پارامترهای $$k$$ و $$h$$، پارامترهای مورد نیاز برای «برازش» (Fitting) مدل روی داده‌های آزمایش است. همچنین، احتمال اینکه همان مورچه $$m+1$$ پل دوم را انتخاب کند، از طریق رابطه $$p_{2} (m+1)= 1- p_{1} (m+1)$$ به دست می‌آید. «شبیه‌سازی مونته کارلو» (Monte Carlo Simulation) انجام شده روی داده‌های آزمایش نشان می‌دهد که مدل توسعه داده شده با مقادیر پارامترهای $$k\approx20$$ و $$h\approx2$$، برازش بسیار خوب و مناسبی از داده‌های آزمایش تولید می‌کند. از این مدل ساده می‌توان برای طراحی «مورچه‌های مصنوعی» (Artificial Ants) استفاده کرد که مسائل بهینه‌سازی را به شیوه مشابه حل می‌کنند.

همان‌طور که پیش از این اشاره شد، ارتباطات غیر مستقیم میان مورچه‌های واقعی از طریق فرومون منتشر شده در محیط انجام می‌شود. به طور مشابه، مورچه‌های مصنوعی می‌توانند فرآیند انتشار فرومون در محیط را از طریق دستکاری مقادیر متغیرهای فرومون متناظر با متغیرهای مسأله شبیه‌سازی کنند. متغیرهای مسأله می‌توانند متناظر با حالاتی در نظر گرفته شوند که مورچه‌های مصنوعی در طول فرآیند تولید جواب بهینه در محیط، با آن‌ها برخورد می‌کنند. همچنین، براساس مدل ارتباطی مبتنی بر فرمون (مدل نشانه‌ورزی)، مورچه‌های مصنوعی به اطلاعات مرتبط با متغیرهای فرومون (متغیرهای مسأله) تنها دسترسی محلی خواهند داشت.

بنابراین، مورچه‌های مصنوعی به دو روش قادر خواهند بود خود را با ویژگی‌های شاخص مدل ارتباطی ذکر شده (نشانه‌ورزی) سازگار کنند:

1. ایجاد تناظر میان متغیرهای توصیف کننده حالات محیطی و مقادیر مختلف برای متغیرهای مسأله.
2. فراهم کردن دسترسی (فقط) محلی به این متغیرها برای عوامل (مورچه‌های مصنوعی).

یکی دیگر از ویژگی‌های رفتاری مهم جمعیت مورچه‌ها که می‌تواند توسط مورچه‌های مصنوعی (عامل‌های روش بهینه‌سازی) مورد بهره‌وری قرار بگیرد، جفت‌شدگی (رابطه متقابل) میان مکانیزم خودکاتالیز و «ارزیابی ضمنی» (Implicit Evaluation) جواب‌ها است. منظور از ارزیابی ضمنی در رفتار بهینه مورچه‌ها این است که مسیر‌های کوتاه‌تر، زودتر از مسیرهای بلندتر توسط مورچه‌ها پیموده می‌شوند؛ در نتیجه، رد فرمون منتشر شده در این مسیر، سریع‌تر توسط مورچه‌های دیگر تقویت می‌شود. مسیر کوتاه‌تر برای مورچه‌های مصنوعی، معادل برازندگی بیشتر یا هزینه کمتر است. بنابراین، جفت‌شدگی میان مکانیزم خودکاتالیز و ارزیابی ضمنی، در صورتی که برای تولید عملگرهای تکاملی مناسب استفاده شود، مکانیزم فوق‌العاده قدرتمندی برای تضمین عملکرد بهینه در الگوریتم‌های بهینه‌سازی مبتنی بر جمعیت خواهد بود.

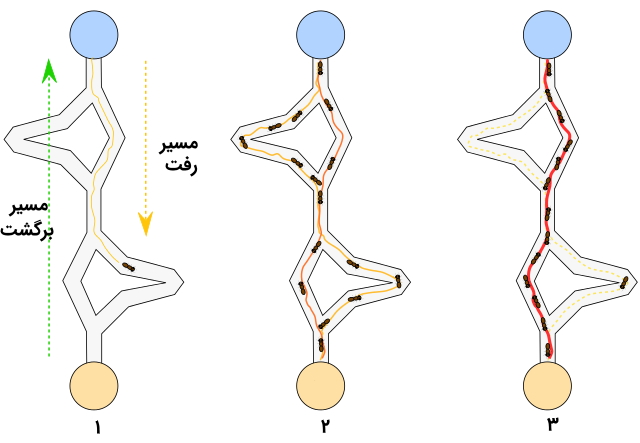
یکی از ویژگی‌های مهم روش الگوریتم کلونی مورچگان، شباهت زیاد میان مکانیزم‌های زیستی مورچگان و رفتارهای شبیه‌سازی شده از کلونی مورچگان در آن است. به عبارت دیگر، شبیه‌سازی و ترکیب ویژگی‌های رفتاری نظیر نشانه‌ورزی، ارزیابی ضمنی جواب‌ها و مکانیزم خودکاتالیز، پایه و اساس الگوریتم مورچگان را تشکیل می‌دهند. بنابراین، شباهت زیادی میان مورچه‌های مصنوعی و مورچه‌های واقعی وجود دارد.

شباهت‌های میان کلونی واقعی مورچگان و کلونی مصنوعی مورچگان (روش بهینه‌سازی)

• جمعیت کلونی‌های واقعی و کلونی‌های مصنوعی مورچگان، از نمونه‌هایی تشکیل شده‌اند که برای رسیدن به یک هدف خاص با هم همکاری می‌کنند. یک کلونی، جمعیتی متشکل از عامل‌های ساده، مستقل و «ناهمگام» (Asynchronous) است که با یکدیگر برای یافتن جواب‌های بهینه یک مسأله بهینه‌سازی، همکاری و تعامل می‌کنند.
• در کلونی مورچگان واقعی، مسأله، پیدا کردن منابع غذایی است. در کلونی مورچه‌های مصنوعی، مسأله، پیدا کردن جواب‌های بهینه برای مسأله بهینه‌سازی داده شده است.
• یک مورچه (چه واقعی و چه مصنوعی)، به تنهایی قادر به پیدا کردن جواب خواهد بود؛ ولی فقط همکاری میان نمونه‌ها از طریق مکانیزم «نشانه‌ورزی» (Stigmergy)، رسیدن به جواب بهینه را تضمین می‌کند.
• وجود مکانیزمی معادل تبخیر فیزیکی اثر فرومون در روش‌های بهینه‌سازی مورچگان (همانند کلونی واقعی مورچگان)، به مورچه‌های مصنوعی این امکان می‌دهد که مسیرهای از پیش پیموده شده را فراموش کرده و بیشتر بر روی جهت‌های جستجوی جدید و امیدوارکننده تمرکز کنند.
• در کلونی مصنوعی مورچگان (همانند کلونی واقعی)، مورچه‌های مصنوعی، جواب‌های کاندید را با حرکت ترتیبی از یک حالت خاص مسأله به حالتی دیگر (تغییر مقادیر متغیرهای مسأله) تولید می‌کنند.
• مورچه‌های واقعی، بر اساس غلظت فرومون در محیط و نیز یک سیاست تصمیم‌گیری تصادفی، مسیر حرکت خود را مشخص می‌کنند. مورچه‌های مصنوعی نیز مرحله به مرحله و از طریق تغییر مقادیر متغیرهای مسأله و نیز تصمیم‌گیری‌های تصادفی، اقدام به تولید جواب‌های کاندید برای مسأله مورد نظر می‌کنند.

تفاوت‌های میان کلونی واقعی مورچگان و کلونی مصنوعی مورچگان (روش بهینه سازی)

• در کلونی واقعی، مورچه‌ها یا ماده‌ای به نام فرومون در محیط منتشر می‌کنند و یا به آن واکنش نشان می‌دهند؛ در کلونی مصنوعی، مورچه‌های مصنوعی، مقادیر عددی متناظر با حالت‌های مختلف مسأله (متغیرهای مسأله) را تغییر می‌دهند. به مقادیر عددی، «فرومون‌های مصنوعی» (Artificial Pheromones) و به دنباله‌ای از این مقادیر عددی، «رد مصنوعی فرومون» (َArtifical Pheromone Trail) گفته می‌شود.
•  برخلاف مورچه‌های واقعی، مورچه‌های مصنوعی در یک جهان گسسته فعالیت می‌کنند. آن‌ها، پی در پی و در یک فضای متناهی متشکل از حالات (متغیرهای) مسأله در حال حرکت و تولید جواب‌های کاندید هستند.
• فرآیند به‌روز رسانی مقادیر فرومون‌ها (نظیر انتشار و تبخیر فرومون) در کلونی مصنوعی مورچگان، دقیقا همانند کلونی واقعی مورچه‌ها انجام نمی‌شود. برخی مواقع، به‌روز رسانی فرومون، فقط توسط تعدادی از مورچه‌های مصنوعی و معمولا تنها پس از تولید یک جواب برای مسأله بهینه‌سازی انجام می‌شود.
• برخی از پیاده‌سازی‌های انجام شده از الگوریتم کلونی مورچگان، مکانیزم‌های اضافی را شامل می‌شوند که در جهان واقعی وجود ندارند (نظیر مکانیزم جستجوی محلی، مکانیزم عقب‌نشینی و سایر موارد).

روش فرا اکتشافی الگوریتم کلونی مورچگان

الگوریتم کلونی مورچگان، به عنوان یک روش فرا اکتشافی برای حل «مسائل بهینه‌سازی ترکیبیاتی» (Combinatorial Optimization Problems) طراحی شده و تاکنون، در موارد بسیاری، برای حل این دسته از مسائل استفاده شده است.

مدل فرومون برای حل مسائل بهینه‌سازی ترکیبیاتی

با فرض داشتن یک مسأله بهینه‌سازی ترکیبیاتی، اولین قدم در بهینه‌سازی با استفاده از الگوریتم کلونی مورچگان، تعریف یک مدل مناسب است. از این مدل، برای تعریف یکی از مهم‌ترین واحدهای الگوریتم کلونی مورچگان یا همان «مدل فرومون» (Pheromone Model) استفاده می‌شود. مدل لازم برای یک مسأله بهینه‌سازی ترکیبیاتی، به شکل زیر تعریف می‌شود:

$$A \;model \;P=(S, \Omega, f)$$

یک مدل فرومون برای یک مسأله بهینه‌سازی ترکیبیاتی شامل موارد زیر خواهد بود:

• یک فضای جستجو به نام $$S$$، که روی مجموعه‌ای متناهی از متغیرهای گسسته تصمیم و مجموعه‌ای از قیدهای تعریف شده روی متغیرهای مسأله به نام $$\Omega$$ تعریف می‌شود.
• یک تابع هدف  $$f: S\rightarrow R_0^+$$ که قرار است کمینه شود. به این نکته باید توجه کرد که کمینه‌سازی یک تابع هدف مثل $$f$$، دقیقا برابر با بیشینه‌سازی تابع هدف $$-f$$ خواهد بود. در نتیجه، هر مسأله بهینه‌سازی ترکیبی، در قالب یک مسأله کمینه‌سازی قابل بازنویسی خواهد بود.

فضای جستجو به این شکل تعریف می‌شود: مجموعه‌ای از متغیرهای تصمیم گسسته (متغیرهای مسأله) $$X_{i}$$، $$i=1,...,n$$، با مقادیر $$v_i^j \in D_{i}=\left\{v_i^1,.....,v_i^{\mid(D_{i})\mid}\right\}$$ داده شده است. مقداردهی متغیرهای مسأله (اختصاص دادن مقدار $$v_i^j$$ به متغیر $$X_{i}$$)، توسط نماد $$X_{i} \leftarrow v_i^j$$ نمایش داده می‌شود. یک جواب کاندید $$s \in S$$، به یک مقداردهی کامل به متغیرهای مسأله گفته می‌شود که در آن، هر متغیر تصمیم مقادیری دارد که تمام قیدهای تعریف شده در مجموعه $$\Omega$$ برای یک مسأله بهینه‌سازی ترکیبیاتی داده شده را ارضا می‌کند.

اگر مجموعه $$\Omega$$ تهی باشد، به $$P$$ مسأله بهینه‌سازی ترکیبی «نامقید» (Unconstrained) گفته می‌شود؛ در غیر این صورت، به آن مسأله بهینه‌سازی «مقید» (Constrained) گفته می‌شود.

یک جواب کاندید $$s* \in S$$، یک «جواب بهینه سراسری» (Global Optimum Solution) برای مسأله بهینه‌سازی ترکیبیاتی داده شده است، اگر و تنها اگر شرط $$f(s*)\leq f(s)\; \forall s\in S$$ را ارضا کند. مجموعه تمامی جواب‌های بهینه سراسری توسط نماد $$S*\subseteq S$$ نمایش داده می‌شوند. حل یک مسأله بهینه‌سازی ترکیبیاتی، مستلزم پیدا کردن حداقل یک جواب بهینه $$s*\in S*$$ است.

از مدل تعریف شده بالا، برای توسعه مدل فرومون در الگوریتم کلونی مورچگان استفاده می‌شود. متغیر تصمیم مقداردهی اولیه شده $$X_{i}=v_i^j$$ (به عبارت دیگر، یک مقدار مانند $$v_i^j$$ از دامنه $$D_{i}$$ به متغیر $$X_{i}$$ اختصاص داده می‌شود)، یک «مؤلفه جواب کاندید» (Candidate Solution Component) نامیده می‌شود و به وسیله نماد $$c_{i,j}$$ نمایش داده می‌شود. مجموعه تمامی مؤلفه‌های جواب کاندید ممکن، توسط $$C$$ نمایش داده می‌شوند. سپس، هر پارامتر «رد فرومون» (Pheromone Trail)، $$T_{ij}$$، متناظر با یکی از مؤلفه‌های جواب کاندید $$c_{i,j}$$ در نظر گرفته می‌شود. مجموعه تمامی پارامترهای رد فرومون، توسط $$T$$ نمایش داده می‌شوند. مقدار یک پارامتر رد فرومون $$T_{ij}$$ توسط نماد $$\tau_{ij}$$ نمایش داده شده و «مقدار فرومون» (Pheromone Value) نامیده می‌شود.

مقادیر فرومون، در طی فرآیند جستجو، توسط الگوریتم کلونی مورچگان استفاده و به روز رسانی می‌شوند. همچنین، این پارامترها امکان مدل‌سازی توزیع احتمالی مؤلفه‌های مختلف جواب را به الگوریتم مورچگان می‌دهند. مقادیر فرومون و جواب کاندید (مقادیر متغیرهای مسأله)، عملا دو مفهوم کاملا به هم وابسته هستند. در طول فرآیند تکاملی، مقادیر فرومون برای جواب‌های کاندیدی که به جواب بهینه سراسری نزدیک‌تر باشند، افزایش می‌یابند و برعکس. در نتیجه، رد فرومون جواب‌های خوب، قوی‌تر می‌شود و جهت جستجو برای یافتن جواب بهینه برای مورچه‌های مصنوعی دیگر مشخص می‌شود.

نمایش فضای مسأله بهینه‌سازی در قالب گراف کاملا متصل

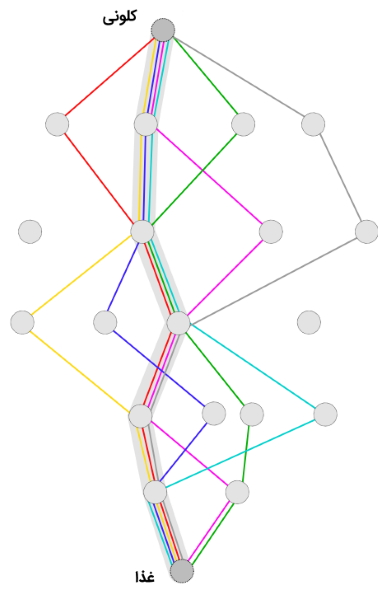
در الگوریتم کلونی مورچگان، مورچه‌های مصنوعی، یک جواب کاندید برای مسأله بهینه‌سازی ترکیبیاتی داده شده را از طریق پیمایش گرافی به نام «گراف ساختاری» (Construction Graph) تولید می‌کنند. این گراف، توسط $$G_{C} (V, E)$$ نمایش داده می‌شود. یک گراف ساختاری کاملا متصل، از مجموعه‌ای از «رأس‌ها» (Vertices) و مجموعه‌ای از «یال‌ها» (Edges) تشکیل شده است. مجموعه مؤلفه‌های جواب کاندید $$C$$ ممکن است متناظر با مجموعه رأس‌ها $$V$$ در گراف $$G_{C}$$ یا مجموعه یال‌ها $$E$$ در گراف $$G_{C}$$ باشند.

مورچه‌ها، برای تولید جواب کاندید، در راستای یال‌های گراف، از یک رأس به رأس دیگر حرکت می‌کنند و از این طریق، به طور تدریجی یک «جواب کاندید جزئی» (Partial Candidate Solution) را تولید می‌کنند. علاوه بر این، مورچه‌ها در هنگام حرکت در محیط، روی یال‌ها یا رأس‌هایی که در گراف ساختاری پیمایش می‌کنند، مقدار مشخصی فرومون منتشر می‌کنند. مقدار فرومون منتشر شده در محیط $$\triangle \tau$$، به کیفیت جواب کاندید تولید شده بستگی دارد. مورچه‌های بعدی، از اطلاعات فرومون منتشر شده به عنوان راهنما برای پیدا کردن مناطق بهتر در فضای جستجو و حرکت به سمت آن‌ها استفاده می‌کنند. از یک سو، این مناطق، به احتمال زیاد حاوی جواب بهینه سراسری هستند و از سوی دیگر، در صورت حرکت مورچه‌‎های مصنوعی به سمت این مناطق، با سرعت بیشتری می‌توانند به جواب بهینه سراسری همگرا شوند.

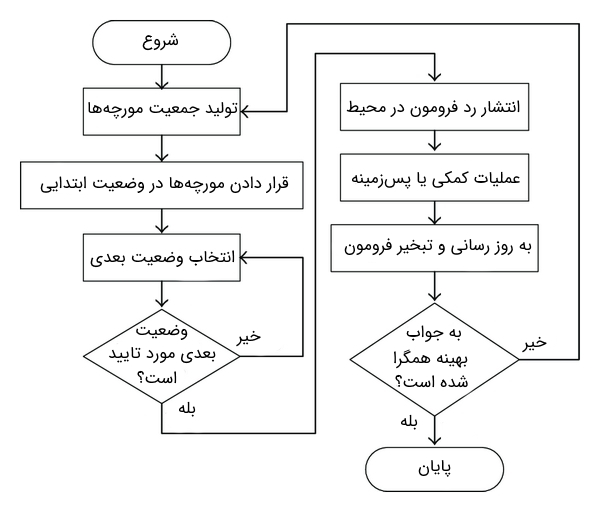
شبه کد الگوریتم کلونی مورچگان در ادامه آمده است.

1. پارامترهای الگوریتم کلونی مورچگان تنظیم شده و ردهای فرومون مقداردهی اولیه می‌شوند.
2. تا زمانی که شرط توقف ارضا نشده باشد:
   • مرحله اول یا مرحله «تولید جواب‌های کاندید» (Construct Ant Solution) را شروع کن.
   • مرحله دوم یا مرحله «جستجوی محلی جواب‌ها» (Local Search) را شروع کن. در این مرحله، از جواب‌های بهینه محلی استفاده می‌شود تا مشخص شود کدام یک از فرومون‌ها باید به روز رسانی شوند. این مرحله اختیاری است و در برخی از پیاده‌سازی‌های انجام شده از الگوریتم کلونی مورچگان وجود ندارد.
   • مرحله سوم یا مرحله «به روز رسانی فرومون» (Pheromone Update) را انجام بده.
3. در صورتی که شرط توقف ارضا شده باشد، اجرای الگوریتم را متوقف کن؛ در غیر این صورت، مراحل را مجددا انجام بده.

الگوریتم کلونی مورچگان از دو بخش تشکیل شده است. در بخش اول، مقادیر پارامترهای مسأله تنظیم و متغیرهای جمعیت اولیه مقداردهی می‌شوند. بخش دو شامل یک حلقه تکرار است که سه مرحله الگوریتم کلونی مورچگان را اجرا می‌کند. در هر حلقه از الگوریتم کلونی مورچگان، جواب‌های کاندید توسط تمامی مورچه‌های مصنوعی ساخته می‌شوند. جواب‌های تولید شده، از طریق یک الگوریتم جستجوی محلی بهبود می‌یابند. در مرحله آخر، فرومون‌ها به روز رسانی می‌شوند.

در ادامه، سه مرحله اصلی الگوریتم کلونی مورچگان با جزئیات بیشتری توضیح داده می‌شود.

مرحله اول: «تولید جواب‌های کاندید» (Construct Ant Solution)

در این مرحله، مجموعه‌ای از $$m$$ مورچه مصنوعی، جواب‌های کاندید مسأله بهینه‌سازی ترکیبیاتی را با استفاده از عناصر یک مجموعه متناهی از «مؤلفه‌های جواب کاندید» در دسترس $$C=\left\{c_{ij}\right\},\; i=1,....,n,\;j=1,....., \mid D_{i}\mid$$ تولید می‌‌کنند. مرحله تولید جواب‌های کاندید با تولید یک جواب کاندید جزئی $$s^{p}=\varnothing$$ آغاز می‌شود. سپس، در گام‌های بعدی از تولید جواب‌های کاندید، جواب کاندید جزئی تولید شده $$s^{p}$$، با اضافه کردن یک مؤلفه از مجموعه «همسایگان امکان‌پذیر» (Feasible Neighbors) $$N (s^{p})\subseteq C$$، گسترده‌تر می‌شود.

فرآیند تولید جواب‌های کاندید را می‌توان به عنوان یک مسیر در گراف ساختاری $$G_{C} =(V, E)$$ در نظر گرفت. به عبارت دیگر، منظور از گسترش جواب بهینه، مشخص کردن مسیر‌های حرکتی ممکن برای مورچه مصنوعی در گراف ساختار مدل فرومون است. از طریق چنین روشی، مناطق همسایگی جواب کاندید جزئی جستجو می‌شود تا بهترین مسیر در جهت جواب بهینه سراسری مشخص شود. مسیرهای مجاز در گراف $$G_{C}$$، به طور ضمنی توسط مکانیزم تولید جواب تعریف می‌شوند. مکانیزم تولید جواب، مجموعه همسایگان امکان‌پذیر $$N (s^{p})\subseteq C$$ را نسبت به هر کدام از جواب‌های جزئی و به طور مجزا تعریف می‌کند.

در هر مرحله از تولید جواب‌های کاندید، نحوه انتخاب مؤلفه‌های مجموعه همسایگان امکان‌پذیر برای گسترش جواب کاندید جزئی، به صورت کاملا احتمالی انجام می‌شود. قوانین لازم برای انتخاب یک مؤلفه از مجموعه همسایگان امکان‌پذیر، در پیاده‌سازی‌های مختلف از الگوریتم کلونی مورچگان، متفاوت از هم هستند. با این حال، شناخته شده‌ترین قانون، مربوط به الگوریتم «سیستم مورچگان» (Ant System) است:

$$p(c_{ij}\mid s^{p})=\frac{\tau_{ij}^\alpha . \eta (c_{ij})^{\beta}}{\sum_{c_{il}\in N(s^{p})}^{} \tau_{il}^\alpha . \eta (c_{il})^{\beta}} , \; \forall c_{ij}\in N(s^{p})$$

در این رابطه، $$\tau_{ij}$$ مقادیر فرومون متناظر با مؤلفه $$c_{ij}$$ و $$\eta(.)$$، تابعی است که در هر مرحله از تولید جواب کاندید، یک مقدار به اصطلاح «اکتشافی» (Heuristic) را به هر [مؤلفه] جواب کاندید $$c_{ij} \in N (s^{p})$$ اختصاص می‌دهد. مقادیر اکتشافی تولید شده توسط تابع $$\eta(.)$$، «اطلاعات اکتشافی» (Heuristic Information) نامیده می‌شوند. همچنین، پارامترهای $$\alpha$$ و $$\beta$$، پارامترهایی با مقادیر مثبت هستند که مقدارشان، میزان اهمیت نسبی (وزن) اطلاعات فرومون (مقادیر متغیرهای یک جواب کاندید) و اطلاعات اکتشافی، در تولید مقدار احتمالی رابطه بالا را مشخص می‌کنند. این رابطه، تعمیمی از مدل ریاضی ارائه شده در بخش‌های قبل، برای توصیف رفتار بهینه مورچگان در آزمایش «پل باینری» (Binary Bridge Experiment) محسوب می‌شود.

فلوچارت ساده الگوریتم کلونی مورچگان در شکل زیر آمده است.

مرحله دوم: «جستجوی محلی جواب‌ها» (Local Search)

بسته به پیاده‌سازی انجام شده از الگوریتم کلونی مورچگان، پس از تولید جواب‌های کاندید و پیش از اینکه فرومون‌ها به روز رسانی شوند، ممکن است فرآیندهای اضافی برای تضمین عملکرد بهینه الگوریتم ضروری باشند. بنابراین، این مرحله، اختیاری است. طبیعت این فرآیندها، ازدحامی است. یعنی توسط فقط یک مورچه مصنوعی قابل انجام نیست. به این دسته از فرآیندها، «عملیات کمکی یا پس‌زمینه» (Daemon Actions) گفته می‌شود.

شایع‌ترین عملیات پس‌زمینه در الگوریتم‌های مبتنی بر الگوریتم کلونی مورچگان، به‌کارگیری جستجوی محلی در جواب‌های کاندید تولید شده است. به‌عنوان نمونه، از جواب بهینه شده محلی برای تصمیم‌گیری در مورد به روز رسانی مقادیر فرومون‌ها استفاده می‌شود.

مرحله سوم: «به روز رسانی فرومون» (Pheromone Update)

هدف مرحله به روز رسانی فرومون، افزایش مقادیر فرومون متناظر با جواب‌های کاندید خوب و بهینه و کاهش مقادیر فرومون متناظر با جواب‌های بد است. چنین کاری، از طریق دو فرآیند عمده انجام می‌شود:

1. کاهش مقادیر فرومون متناظر با تمامی جواب‌های کاندید از طریق فرآیند «تبخیر فرومون» (Pheromone Evaporation)
2. افزایش مقادیر فرومون متناظر با جواب‌های کاندید عضو مجموعه «جواب‌های خوب» یا $$S_{upd}$$

این دو فرآیند از طریق رابطه زیر کنترل می‌شوند. به رابطه زیر، «قانون به روز رسانی فرومون» گفته می‌شود.

$$\tau_{ij} \leftarrow (1-\rho) \tau_{ij} + \rho \sum_ {s \in S_{upd} \mid c_{ij} \in s } ^ {} F(s)$$

بخش اول این رابطه، فرآیند تبخیر فرومون (کاهش مقدار فرومون تمامی جواب‌های کاندید) را کنترل می‌کند. بخش دوم آن، تنها مقادیر فرومون متناظر با جواب‌های کاندید عضو مجموعه «جواب‌های خوب» یا $$S_{upd}$$ را افزایش می‌دهد. در این رابطه، $$S_{upd}$$ مجموعه جواب‌های کاندیدی را شامل می‌شود که برازندگی بالایی دارند؛ یعنی به جواب بهینه سراسری نزدیک‌تر هستند. پارامتر $$\rho \in \; (0, 1]$$، «نرخ تبخیر» (Evaporation Rate) نام دارد و $$F : S \rightarrow R _ 0 ^ +$$، «تابع برازندگی» (Fitness Function) نام دارد.

به‌ بیان ساده، این فرآیند منجر به افزایش مقدار فرومون متناظر با مورچه‌هایی می‌شود که در بهترین مسیر‌های موجود به سمت جواب بهینه قرار دارند (به جواب بهینه نزدیک‌ترند) و دارای برازندگی بالاتری (هزینه کمتر یا سود بیشتر) هستند. در نتیجه، مورچه‌های دیگر نیز به این مسیر همگرا می‌شوند.

وجود پارامتر تبخیر فرومون، برای جلوگیری از «همگرایی سریع و نابالغِ» (Rapid and Premature Convergence) الگوریتم کلونی مورچگان ضروری است. پارامتر تبخیر، نوعی مکانیزم «فراموشی» (Forgetting) در فرآیند بهینه‌سازی فراهم می‌کند و سبب تاکید بیشتر بر جستجو و کاوش مناطق جدید، در فضای جستجوی الگوریتم‌های پیاده‌سازی شده مبتنی بر الگوریتم کلونی مورچگان می‌شود.

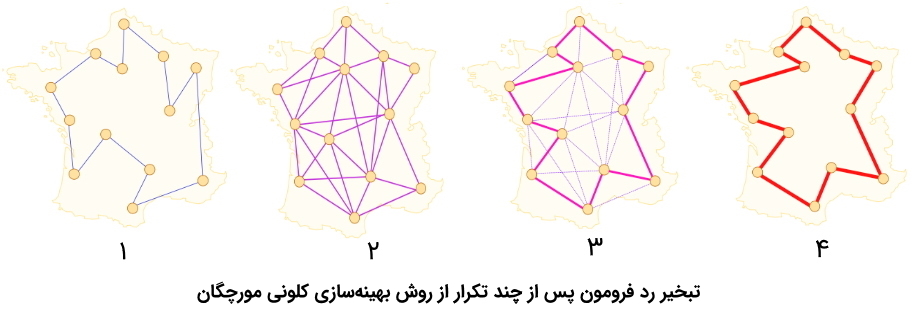
بیشتر تفاوت موجود میان پیاده‌سازی‌های گوناگون انجام شده از الگوریتم کلونی مورچگان، به قانون به روز رسانی فرومون‌ها و نحوه مشخص کردن جواب‌های کاندید عضو مجموعه «جواب‌های خوب» یا $$S_{upd}$$ مرتبط است. یکی از مهم‌ترین بخش‌های مرحله به روز رسانی فرومون‌ها، انتخاب اعضای مجموعه «جواب‌های خوب» $$S_{upd}$$ است.

در بیشتر الگوریتم‌های تکاملی مبتنی بر الگوریتم کلونی مورچگان، $$S_{upd}$$ زیرمجموعه‌ای از $$S_{ iter } \cup \left\{ s_{ bs } \right\}$$ تعریف می‌شود. در این رابطه، $$S_{ iter }$$ مجموعه جواب‌های کاندید تولیده شده در تکرار کنونی است، و $$s_{ bs }$$ مجموعه بهترین جواب‌های کاندید پیدا شده از اولین تکرار الگوریتم تاکنون است.

به عنوان نمونه، در قانون به روز رسانی فرومون الگوریتم سیستم مورچگان، مجموعه جواب‌های کاندید عضو مجموعه «جواب‌های خوب» از طریق رابطه $$S _ { upd } \leftarrow S _ { iter }$$ مشخص می‌شوند.

در صورتی که در قانون به روز رسانی فرومون‌ها، تاکید بیشتری روی استفاده از جواب‌های خوب هر نسل برای به روز رسانی باشد، سرعت دستیابی به جواب‌های خوب بهینه افزایش می‌یابد. با این حال، احتمال همگرایی نابالغ افزایش پیدا می‌کند. معمولا توصیه می‌شود که در هنگام پیاده‌سازی قانون به روز رسانی فرومون، مکانیزم‌هایی طراحی شوند تا از همگرایی سریع و نابالغ الگوریتم جلوگیری شود.

مزایای روش الگوریتم کلونی مورچگان

• همکاری گروهی میان مورچه‌ها برای تولید جواب‌های بهینه، طبیعت مبتنی‌بر «توازی» (Parallelism) و «همبستگی» (Solidarity) این روش فرا اکتشافی را نشان می‌دهد.
• بازخورد مثبت ایجاد شده از طریق انتشار فرومون در محیط، سبب همگرایی سریع به جواب‌های خوب برای مسأله بهینه‌سازی می‌شود.
• برای استفاده در کاربردهای پویا (کاربردهایی که نیاز به انطباق سریع با تغییرات محیطی ضروری است) مناسب است.
• همگرایی به جواب بهینه، تضمین شده است.

معایب روش الگوریتم کلونی مورچگان

• تجزیه و تحلیل نظری این روش بسیار سخت است.
• این روش، بر پایه دنباله‌ای از تصمیمات تصادفی ولی وابسته به هم بنا نهاده شده است.
• زمان لازم برای همگرایی به جواب بهینه نامشخص است.

استفاده از الگوریتم کلونی مورچگان برای حل «مسأله فروشنده دوره‌گرد» (TSP)

یکی از محبوب‌ترین روش‌ها برای نمایش چگونگی عملکرد روش فرا اکتشافی الگوریتم کلونی مورچگان، استفاده از آن در حل مسأله فروشنده دوره‌گرد است. این مسأله، از مجموعه‌ای از شهرها (مکان‌ها) و یک فروشنده دوره‌گرد تشکیل شده است. این فروشنده اجازه دارد از هر شهر تنها یک‌بار عبور کند. فاصله میان شهرها داده شده است و هدف پیدا کردن «تور همیلتونی» (Hamilton Cycle) با طول کمینه است. پیچیدگی این مسأله برابر با «ان‌پی هارد» (NP-hard) است.

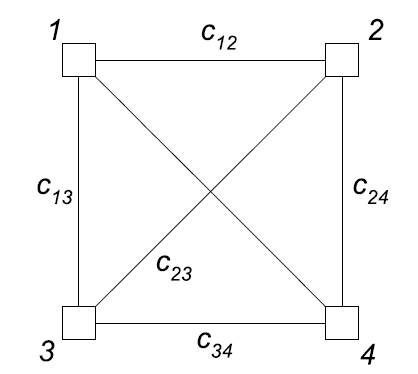
کاربرد بهینه‌سازی کلونی مورچگان برای حل مسأله فروشنده دوره‌گرد ساده و صریح است. حرکت میان شهرها (مکان‌ها)، مؤلفه‌های جواب کاندید است؛ یعنی، حرکت از شهر $$i$$ به شهر $$j$$، مولفه جواب کاندید $$C _ { ij } \equiv C _ { ji }$$ مسأله خواهد بود. گراف ساختاری $$G_{C} =(V, E)$$ از طریق ایجاد تناظر میان مجموعه شهرها با مجموعه رأس‌ها V در گراف ساختاری تعریف می‌شود.

از آنجا که هیچ محدودیتی در امکان حرکت از یک شهر به هر  شهر دیگری وجود ندارد، گراف ساختاری تشکیل شده یک گراف کاملا متصل است و تعداد رأس‌های موجود در گراف برابر تعداد شهرهای تعریف شده در مسأله خواهد بود. همچنین، اندازه یال‌های گراف متناسب با فاصله شهرها (با رأس‌ها نمایش داده می‌شوند) از یکدیگر است. فرومون نیز متناظر با مجموعه یال‌ها E در گراف ساختاری خواهد بود.

نمونه‌ای از یک گراف کامل متصل برای مسأله فروشنده دروه‌گرد با تعداد چهار شهر در شکل زیر آمده است.

مورچه‌ها به شکلی که در ادامه بیان شده است، اقدام به تولید جواب‌های مسأله می‌کنند. هر کدام از مورچه‌ها، از یک شهر (یک رأس در گراف) کاملا تصادفی شروع می‌کنند. سپس، در هر گام از فرآیند تولید جواب، در راستای یال‌های گراف به حرکت می‌پردازند. هر مورچه، مسیر پیموده شده در گراف را به خاطر می‌سپارد و در گام‌های بعدی، یال‌هایی را برای حرکت در گراف انتخاب می‌کند که به مکان‌های (رأس‌های) از پیش پیموده شده منتهی نشوند. به محض اینکه تمامی رأس‌های گراف توسط یک مورچه پیمایش شد، یک جواب کاندید تولید می‌شود.

در هر گام از فرآیند تولید جواب، مورچه‌ها به طور احتمالی، از میان یال‌های در دسترس (یال‌های پیموده نشده و منتهی به رأس‌هایی که از آن‌ها گذر نکرده)، یک یال را برای پیمایش انتخاب می‌کنند. نحوه محاسبه احتمال انتخاب یال‌ها، به پیاده‌سازی انجام شده از الگوریتم کلونی مورچگان بستگی دارد. پس از اینکه تمامی مورچه‌ها یک جواب کاندید تولید کردند، فرومون روی یال‌ها، براساس «قانون به روز رسانی فرومون» به روز رسانی می‌شود.

پیاده‌سازی الگوریتم کلونی مورچگان برای حل مسأله فروشنده دوره‌گرد در متلب

در این بخش، کد متلب پیاده‌سازی روش بهینه‌سازی کلونی مورچگان برای حل مسأله فروشنده دوره‌گرد آورده شده است. تعداد شهرها (مکان‌ها)، برای مسأله فروشنده دوره‌گرد، برابر با 20 خواهد بود.

مختصات مکانی شهرها در ادامه آمده است.

تعداد تکرارهای بیشینه برای رسیدن به جواب بهینه سراسری مسأله فروشنده دوره‌گرد، برابر با 200 در نظر گرفته شده است. وزن اطلاعات فرومون (پارامتر آلفا) برابر با 1 و وزن اطلاعات اکتشافی نیز برابر با 1 است؛ یعنی اطلاعات فرومون و اطلاعات اکتشافی، به یک اندازه، در تولید احتمال انتخاب هر یک از مؤلفه‌های مجموعه همسایگان امکان‌پذیر برای گسترش جواب کاندید جزئی، سهیم هستند. تعداد جمعیت مورچه‌ها، برابر با 40 است. در هر تکرار، از مقدار برازندگی جواب‌های تولید شده توسط مورچه‌ها برای به روز رسانی مقادیر فرومون استفاده می‌شود.

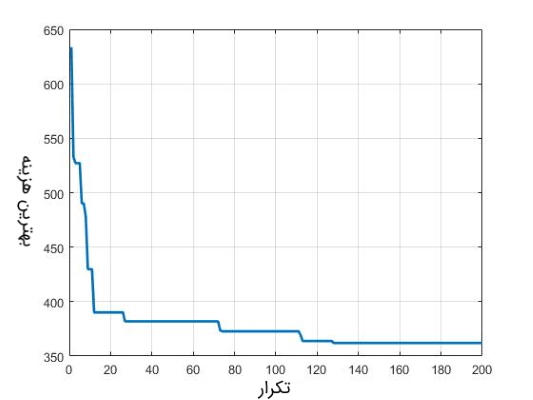
نرخ تبخیر، برای تولید مکانیزم تکاملی و همگرا شونده به جواب بهینه سراسری، برابر با 0٫05 در نظر گرفته شده است. این مقدار، تضمین می‌کند که الگوریتم بهینه‌سازی، جواب‌های کاندید بد را به راحتی فراموش کند و به جستجو برای یافتن جواب بهینه سراسری در دیگر مناطق فضای جستجو ادامه دهد. شکل‌های زیر نحوه همگرایی روش بهینه‌سازی کلونی مورچگان به جواب بهینه سراسری، برای حل مسأله فروشنده دوره‌گرد را نمایش می‌دهند.

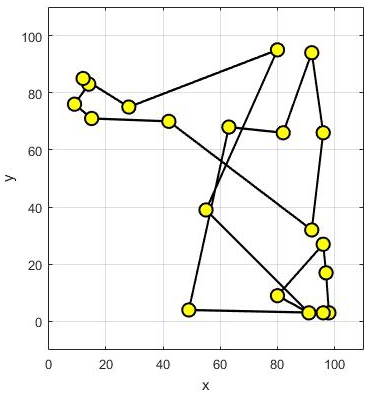
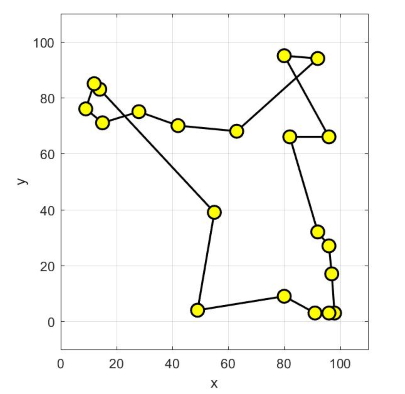
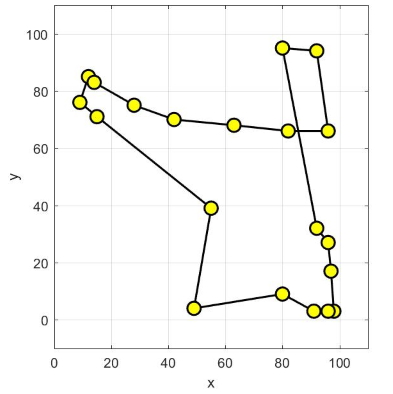
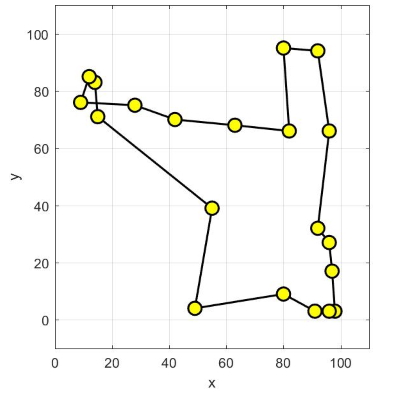
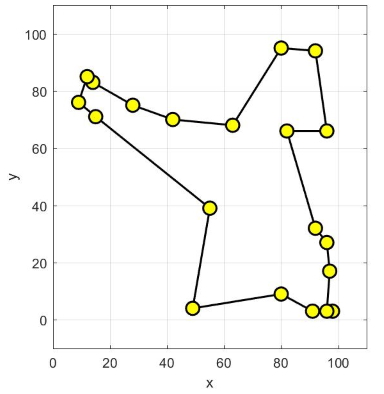
نحوه همگرایی روش بهینه‌سازی کلونی مورچگان به مسیر بهینه در مسأله فروشنده دوره‌گرد در تصویر متحرک زیر نمایش داده شده است.

الگوریتم کلونی مورچگان، در تکرار 128 به جواب بهینه سراسری (مقدار هزینه برابر با 362.۰۳۸) همگرا شده است. شکل زیر، نحوه همگرایی به هزینه بهینه را نشان می‌دهد.

در ادامه، توابع مورد نیاز برای اجرای روش بهینه‌سازی کلونی مورچگان نمایش داده شده‌اند. شایان توجه است که برای اجرای این روش بهینه‌سازی در متلب، ابتدا باید هر کدام از توابع ارائه شده در زیر را در قالب یک فایل تابعی قابل خواندن توسط متلب ذخیره و سپس آن‌ها را اجرا کرد.

تابع اجرایی مؤلفه‌های مختلف الگوریتم کلونی مورچگان برای حل مسأله فروشنده دوره‌گرد

تابع تولید مدل فرومون

تابع محاسبه اندازه طول تور همیلتونی گراف ساختاری

تابع انتخاب در مرحله تولید جواب‌های کاندید

تابع نمایش جواب‌ بهینه تولید شده برای مسأله فروشنده دوره‌گرد

کد اجرای الگوریتم کلونی مورچگان در متلب

کاربردهای الگوریتم کلونی مورچگان

الگوریتم کلونی مورچگان، می‌تواند برای حل مسائل بهینه‌سازی ترکیبیات مختلفی استفاده شود. این الگوریتم تاکنون در کاربردهایی نظیر مسیریابی وسایل نقلیه و بهینه‌سازی استراتژی برنامه‌ریزی کارها مورد استفاده قرار گرفته است. بسیاری از الگوریتم‌های بهینه‌سازی پیاده‌سازی شده بر مبنای این روش، برای حل مسائل بهینه‌سازی متغیرهای حقیقی، مسائل تصادفی و مسائل بهینه‌سازی چندهدفه به کار گرفته شده‌اند.

آزمایشات انجام شده برای تولید جواب بهینه سراسری مسأله فروشنده دوره‌گرد، نشان می‌دهد که این روش می‌تواند جواب بسیار دقیق و نزدیک به جواب بهینه سراسری را تولید کند. از آنجا که این الگوریتم بر پایه ساختار گرافی بنا نهاده شده است، به راحتی می‌تواند خود را با تغییرات پویای محیطی سازگار کند؛ ویژگی‌ای که سبب مزیت این الگوریتم به دیگر الگوریتم‌های بهینه‌سازی نظیر الگوریتم ژنتیک و الگوریتم «شبیه‌سازی تبرید» (Simulated Annealing) شده است. همچنین، قابلیت تطابق با شرایط در حال تغییر محیط عملیاتی، این الگوریتم را به گزینه مناسبی برای کاربردهایی نظیر مسیریابی شبکه و برنامه‌ریزی سیستم‌های حمل و نقل شهری تبدیل کرده است. مهم‌ترین کاربردهای الگوریتم مورچگان عبارتند از:

• مسائل بهینه‌سازی استراتژی برنامه‌ریزی کارها (Job-Scheduling Problems).
• بهینه‌سازی مسیریابی وسایل نقلیه.
• «پردازش تصویر» (Image Processing).
• مسائل بهینه‌سازی اندازه دستگاه‌ها در طراحی فیزیکی دستگاه‌های نانوالکترونیکی.
• بهینه‌سازی شکل آنتن‌ها (به عنوان نمونه در برچسب‌های RF-ID).
• «دسته‌بندی» (Classification).
• «داده‌کاوی» (Data Mining).

دوره ویدیویی آموزش الگوریتم کلونی مورچگان و پیاده سازی آن در MATLAB

در صورتی که به موضوع الگوریتم مورچگان علاقه‌مند هستید، می‌توانید دوره ویدیویی آموزش این الگوریتم و پیاده‌سازی آن در متلب را در وب سایت فرادرس مشاهده کنید. در این دوره آموزشی، ابتدا مروری بر مبانی و مفاهیم اساسی هوش جمعی انجام شده است. سپس، مبانی تئوری الگوریتم کلونی مورچگان و بخش‌های مختلف آن شرح داده شده است. سپس، انواع نسخه‌های الگوریتم کلونی مورچگان مورد بررسی قرار گرفته و در ادامه پیاده‌سازی الگوریتم کلونی مورچگان در متلب انجام شده است. همچنین، مسأله فروشنده دوره‌گرد و روش حل آن با استفاده از این الگوریتم بیان و در متلب پیاده‌سازی شده است. مدرس این دوره آموزشی دکتر سید مصطفی کلامی هریس و مدت زمان دوره 6 ساعت و 47 دقیقه است.

جمع‌بندی

الگوریتم کلونی مورچگان، یکی از روش‌های فرا اکتشافی است که بر پایه رفتار ازدحامی مورچه‌های واقعی برای یافتن منابع غذایی الهام گرفته شده است. مؤلفه اساسی الگوریتم کلونی مورچگان، مدل فرومون است. روش بهینه‌سازی کلونی مورچگان، یک مدل برای پیاده‌سازی الگوریتم‌های بهینه‌‌سازی ارائه می‌دهد.

تاکنون، الگوریتم‌های بهینه‌سازی متفاوتی بر پایه این روش بهینه‌سازی ارائه شده‌اند. از مهم‌ترین پیاده‌سازی‌های انجام شده می‌توان به الگوریتم‌هایی نظیر «سیستم مورچگان» (َAnt System)، «سیستم کلونی مورچگان» (Ant Colony System) و «سیستم مورچگان Min-Max» اشاره کرد. ویژگی مهم این روش، اثرگذاری و انعطاف‌پذیری فوق‌العاده آن در حل مسائل بهینه‌سازی است.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های الگوریتم‌‌های بهینه‌‌سازی هوشمند
• آموزش الگوریتم مورچگان در متلب
• مجموعه آموزش‌‌های هوش مصنوعی
• الگوریتم بهینه سازی فاخته — از صفر تا صد
• رویکرد هوش ازدحامی با استفاده از کلونی زنبور عسل مصنوعی برای حل مسائل بهینه‌سازی
• شبیه‌سازی تبرید (Simulated Annealing) — به زبان ساده

^^