پیچیدگی زمانی الگوریتم های مرتب سازی با نماد O بزرگ — به زبان ساده

از نماد O بزرگ برای توصیف ماهیت مجانبی یک سیستم در زمان رشد ورودی استفاده می‌شود. به طور معمول ما از این نماد برای توصیف زمان اجرای یک الگوریتم بهره می‌گیریم؛ اما از آن برای توصیف پیچیدگی فضایی و یا حتی سیستم‌های خارج از حوزه علوم کامپیوتر نیز می‌توان بهره گرفت. در این نوشته فرض می‌کنیم که این نماد برای توصیف پیچیدگی زمانی یک الگوریتم استفاده می‌شود؛ مگر این که صراحتاً به چیز دیگری اشاره کنیم. بر این اساس، پیچیدگی زمانی الگوریتم های مرتب سازی با نماد O بزرگ را مورد بررسی قرار می‌دهیم.

تحلیل مجانبی

«تحلیل مجانبی» (Asymptotic Analysis) به معنی تمرکز روی چگونگی رشد زمان اجرای یک الگوریتم در زمان رشد ورودی و میل آن به بی‌نهایت است. ورودی معمولاً به صورت n نشان داده می‌شود. همچنان که مجموعه داده‌های ما افزایش می‌یابند، این تابع رشد است که عامل زمان اجرا را تعیین خواهد کرد. برای مثال (O(n نشان می‌دهد که تغییرات زمان اجرا، رابطه‌ای خطی با ورودی n دارند. $$O(n^2)$$ نشان می‌دهد که زمان اجرا رابطه تناسبی با مربع ورودی دارد. در مجموعه داده‌های بزرگ، این وضعیت معمولاً اطلاعات کافی در مورد این که کدام الگوریتم سریع‌تر خواهد بود ارائه می‌کند.

فیلم آموزش طراحی الگوریتم در فرادرس

کلیک کنید

زمانی که خصوصیت مجانبی یک تابع را بررسی می‌کنیم، از ثابت‌ها صرف‌نظر می‌کنیم و همچنین ضرایب و جمله‌های با مراتب پایین را نیز نادیده می‌گیریم. برای نمونه تابع زیر را در نظر بگیرید:

 f(n) = 100 * n * lg(n) + n + 10000

پیچیدگی این تابع به صورت ((O(n * lg(n توصیف می‌شود، زیرا n به سمت بی‌نهایت می‌رود و ثابت و ضرایب در این وضعیت بی‌اهمیت می‌شوند. به نمودارهای زیر توجه کنید:

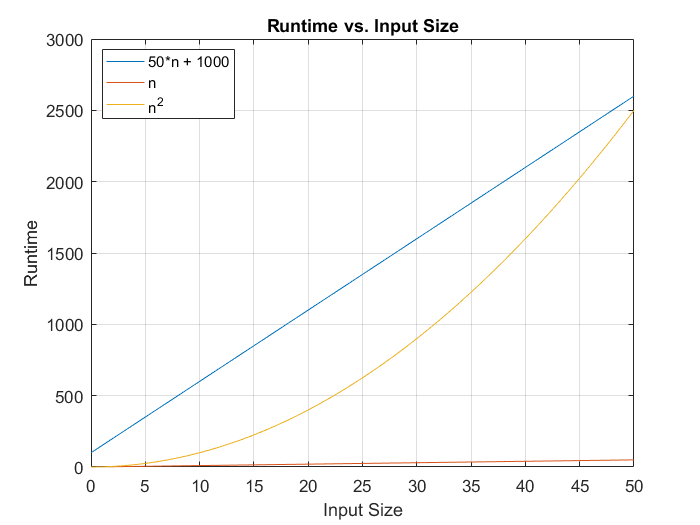
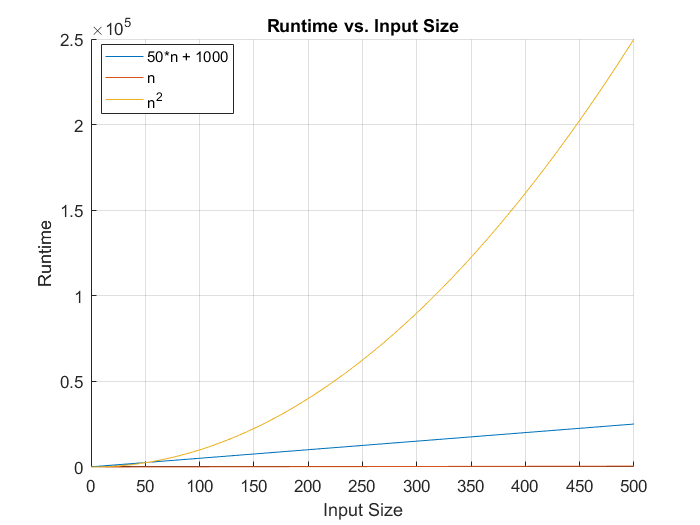
همان طور که می‌بینید در مجموعه داده‌های کوچک، نماد O بزرگ ممکن است چندان گویا نباشد؛ اما حتی افزایش نقاط داده از 50 به 500 در نمودار اول موجب می‌شود که ماهیت مجانبی تابع‌ها مشاهده شود.

بدیهی است که معیارهایی برای بهینه‌سازی کد در چارچوب زمان اجرای مجانبی خاصی جهت افزایش عملکرد وجود دارد؛ اما این کار باید پس از این که مطمئن شدیم الگوریتم مجانبی مناسبی انتخاب شده است، صورت بگیرد.

با این که به نظر می‌رسد O بزرگ به معنی زمان اجرای مجانبی استفاده می‌شود و به توصیف ماهیت «مجانبی تنگ» (tight asymptotic) تابع می‌پردازد (یعنی کران‌های بالا و پایین را همزمان توصیف می‌کند)؛ اما در عمل صحیح نیست. تعاریف رسمی زمان اجرای مجانبی که در کتاب «مقدمه‌ای بر الگوریتم‌ها» (Introduction to Algorithms) نوشته توماس کورمن و همکارانش آمده، به صورت زیر است:

ϴ بزرگ (تتا)

به طور رسمی برای اینکه ((ϴ(g(n به توصیف تابع (f(n بپردازد، باید ثابت‌های c1 ،c2 و n_o مثبتی وجود داشته باشند که رابطه زیر در مورد آن‌ها برقرار باشد:

0 <= c1 * g(n) <= f(n) <= c2 * g(n) for all n >= n_o

برای روشن‌تر شدن موضوع تصور کنید الگوریتمی دارید که به وسیله یک معادله پیچیده (f(n توصیف شده است. شما می‌توانید (f(n را از طریق معادله بسیار ساده (g(n که همه مقادیر ثابت، ضریب و جمله‌های با مرتبه پایین آن حذف شده‌اند، با نمادگذاری تتای بزرگ توصیف کنید، اگر و تنها اگر دو ثابت دلخواه به (g(n اضافه کنید که بتوانند تابع اصلی (f(n شما را که از یک اندازه داده ورودی خاص n_o عبور می‌کند، «ساندویچ» کنند.

مثال: فرض کنید (f(n) = 100*n^2 + 4*n*lg(n باشد. ما می‌توانیم نشان دهیم که n^2 می‌تواند این تعریف را با معادله‌ها و گراف زیر تأمین کند:

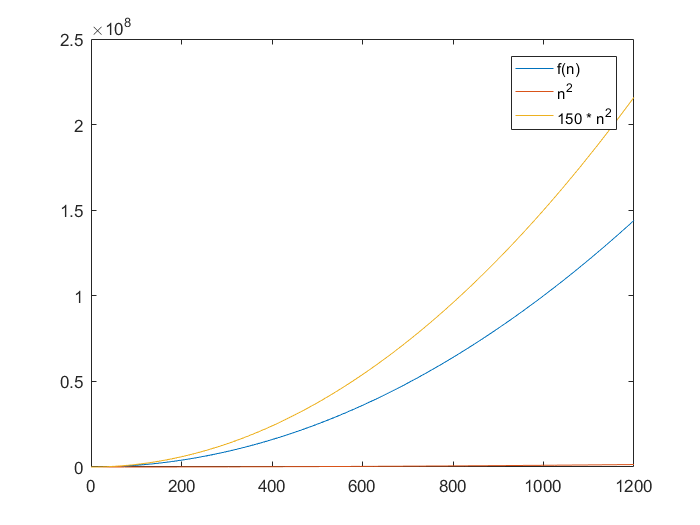
اینک اگر تلاش کنیم تابع (f(n را با nlgn، ساندویچ کنیم، می‌بینیم که کران بالا با رشد n به طور ناگزیر از (f(n عبور می‌کند و مهم نیست که مقدار ثابت را چه مقدار تعیین کرده باشیم:

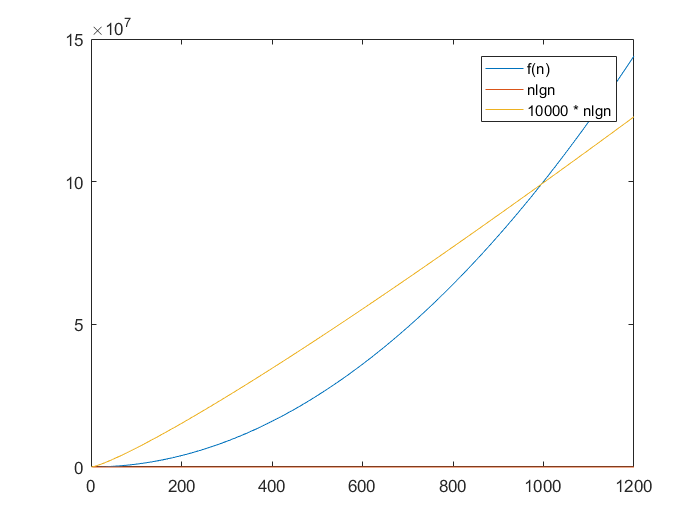
بنابراین از نظر فنی، هر بار که یک تابع با O بزرگ فوق را فراخوانی کنیم، باید به جای (O(n آن را (ϴ(n بنامیم.

O بزرگ

O بزرگ یک کران بالای مجانبی ارائه می‌کند که در تضاد با کران بالا و پایینِ ارائه شده از سوی نماد ϴ است. به طور رسمی، برای این که ((O(g(n بتواند یک تابع (f(n را توصیف کند، باید ثابت c و n_o وجود داشته باشند که رابطه زیر در مورد آن‌ها برقرار باشد:

0 <= f(n) <= c*g(n) for all n >= n_0

بنابراین در واقع این که بگوییم یک الگوریتم که به صورت زیر تعریف شده، دارای پیچیدگی زمانی (O(n^3 است، گفته صحیحی است:

f(n) = 3*n + 100

هر چند در واقع (ϴ(n است و نه (O(n.

همچنین نمادهای کمتر استفاده شده دیگری نیز وجود دارند که به طور مشابه تعریف می‌شوند:

• نماد Ω یا امگای بزرگ صرفاً به تعریف کران پایین مجانبی می‌پردازد.
• نماد o کوچک به تعریف کران بالایی می‌پردازد که از نظر مجانبی تنگ نیست. برای نمونه در مثال فوق ما یک تابع (ϴ(n را دارای پیچیدگی $$O(n^3)$$ توصیف کردیم که ازنظر مجانبی، تنگ نیست و از این رو باید آن را به صورت $$o(n^3)$$ بنویسیم. دقت کنید که (o(n می‌تواند نادرست باشد.
• نماد ω یا امگای کوچک نیز به تعریف یک کران پایین می‌پردازد که نباید از نظر مجانبی تنگ باشد.

زمانی که الگوریتم‌ها را توصیف می‌کنیم، پراستفاده‌ترین مفهوم نماد ϴ است و به طور معمول به صوت نماد O بزرگ نوشته می‌شود.

با این که الگوریتم‌ها می‌توانند به وسیله بهترین حالت، حالت متوسط و بدترین حالت زمان اجرایی‌شان توصیف شوند؛ اما به طور معمول (البته با چند استثنا که در ادامه توضیح داده‌ایم) به 3 دلیل روی سناریوی بد‌ترین حالت متمرکز می‌شویم:

1. محاسبه زمان اجرای بدترین حالت نسبت به مدت میانگین آسان‌تر است، چون عوامل کمتری را باید در نظر گرفت.
2. تحلیل بدترین حالت تضمین می‌کند که دیگر هرگز زمانی بالاتر از این نخواهیم داشت.
3. به طور معمول در زمان پیاده‌سازی در اغلب موارد سناریوی بدترین حالت رخ می‌دهد.

مشخص شد که lgn (لگاریتم n در مبنای 2) برای اغلب بررسی‌های زمان اجرا مهم است. در ادامه مروری کوتاه بر لگاریتم‌ها خواهیم داشت.

لگاریتم تعیین می‌کند که مبنای مورد نظر باید در چه نمایی باشد تا یک عدد خاص تولید شود. برای نمونه از آنجا که مبنای ما 2 است، اگر بخواهیم (lg(8 را پیدا کنیم باید از خود بپرسیم که: «کدام توان 2 است که عدد 8 را به ما می‌دهد؟» در این مورد می‌دانیم که $$2^3$$ برابر با 8 و از این رو lg(8)=3 است. در واقع ما به نوعی تجزیه یک توان می‌پردازیم. این یک مفهوم مهم است، زیرا اگر بتوانیم الگوریتمی بسازیم که به وسیله یک log تعریف می‌شود، با سرعت بسیار کندی رشد پیدا می‌کند. در واقع سرعت رشد آن به همان اندازه‌ای کند است که سرعت رشد نماها تند است و این مقدار بزرگی است.

تصور کنید مجموعه داده‌ای با اندازه 262144 دارید و یک الگوریتم با زمان اجرای f(n) = n را روی آن اجرا می‌کنید. اگر مجموعه داده به اندازه 524288 افزایش یابد، شما به 262144 عملیات بیشتر نیاز خواهید داشت؛ اما اگر f(n) = n^2 باشد، شما به 68719476736 عملیات بیشتر نیاز خواهید داشت. اگر (f(n) = lg(n باشد در این صورت شما به یک 1 عملیات بیشتر نیاز خواهید داشت. در واقع اگر تابع به صورت (f(n) = lg(n باشد، هر زمان که مجموعه داده‌ها دو برابر می‌شود، به 1 عملیات بیشتر نیاز خواهیم داشت.

چرا پیچیدگی زمان اجرایی مهم است؟

زمانی که روی مجموعه داده‌های بزرگ یا مجموعه داده‌ای کار می‌کنیم که با افزایش کاربران و گردآوری اطلاعات، بزرگ می‌شود، زمان اجرای ما بر اساس رشد مجانبی تعیین خواهد شد. همان طور که پیش‌تر گفتیم، ثابت‌ها، ضرایب و جمله‌های با مرتبه پایین تأثیر نسبتاً پایینی در مقایسه با مؤلفه‌های با مرتبه بالا دارند. تفاوت بین الگوریتم ((O(n*lg(n و یک الگوریتم (O(n² به سادگی می‌تواند به میزان تفاوت بین یک اپلیکیشن با عملکرد مناسب و یک اپلیکیشن مطلقاً غیر قابل استفاده باشد.

از نماد O بزرگ چگونه در عمل استفاده کنیم؟

اینک می‌دانیم که چرا باید به الگوریتم‌ها اهمیت بدهیم. اگر مشغول کار روی یک مجموعه داده کوچک باشید و هیچ راهی برای این که این مجموعه افزایش یابد، وجود نداشته باشد، شاید چندان معقول نباشد که زمان خود را صرف توسعه کد کاملاً بهینه بکنید و تلاش نمایید که زمان اجرای بهتری برای الگوریتم خود به دست آورید.

اگر مجموعه داده شما بزرگ است یا احتمال بزرگ شدن آن می‌رود، لازم است که به بررسی چگونگی تأثیرگذاری آن روی زمان اجرا (و البته حافظه) بیندیشید. از این رو باید بتوانید بگویید که زمان اجرای مجانبی کدتان چه قدر است؟ برخی روش‌های این کار به صورت زیر است:

• حلقه‌ها را بررسی کنید. اگر روی یک مجموعه حلقه، تکراری تعریف کرده‌اید که یک بار اجرا می‌شود، احتمالاً باید یک الگوریتم (ϴ(n داشته باشید. اگر حلقه شما، خود دارای یک حلقه درونی است که روی همه داده‌ها (یا در هر اجرای حلقه اصلی n-1 بار) می‌چرخد، احتمالاً با یک الگوریتم (ϴ(n² مواجه هستید که کاملاً خطرناک است.
• از «پشت صحنه» کد خود در زمانی که یک تابع را فراخوانی می‌کنید که خودتان ننوشته‌اید، یا بومی آن زبان است با خبر باشید. ممکن است روش‌های بهتری برای انجام چنین کارهایی وجود داشته باشد. این که از ماهیت متدهایی که فراخوانی می‌کنید ناآگاه باشید، موجب می‌شود که بهینه‌سازی کد بسیار دشوار شود.
• در کد خود به دنبال تابع‌هایی بگردید که به اندازه داده‌های ورودی وابسته هستند و ثابت‌ها، یا تکرار آن کد را که به اندازه داده‌ها وابسته نیست را از بررسی‌های خود کنار بگذارید. بدین ترتیب به روشی بسیار راحت‌تر می‌توانید ((ϴ(g(n را محاسبه کنید.

ذهنیت «تقسیم و حل» داشته باشید

رویکرد «تقسیم و حل» (Divide and Conquer) سه مرحله دارد:

1. مسئله را به مسائلی کوچک‌تر تقسیم کنید.
2. مسائل فرعی را به صورت بازگشتی حل کنید تا این که آن قدر کوچک شوند که یک راه‌حل ساده به دست آمده باشد.
3. راه‌حل‌های مسائل فرعی را با هم ترکیب کنید تا یک راه‌حل جامع به دست آید.

اساساً اگر بتوانید به تقسیم کردن مسئله به نیمه‌های مساوی بپردازید تا زمانی که این مسائل فرعی آن قدر کوچک شوند که حل کردن آن‌ها آسان باشد، در این صورت می‌توانید این مسئله‌های ساده و کوچک را حل کرده و با ترکیب کردن آن‌ها به پاسخ کامل دست پیدا کنید. این احتمال وجود دارد که بدین ترتیب الگوریتم خود را از زمان اجرای (ϴ(n² به (ϴ(nlgn تغییر داده باشید.

دلیل رخ دادن این تبدیل آن است که اگر کد خود را به نیمه‌های مساوی تقسیم کنید، می‌توانید lgn بار این تقسیم را انجام دهید (به عبارت دیگر چند مرتبه می‌توانیم چیزی را در 2 ضرب کنیم تا به اندازه n برسیم؟). هر بار که مسئله خود را به 2 بخش تقسیم می‌کنید، باید چرخه‌ای روی داده‌ها تعریف کنید تا کاری انجام دهد و از این رو پیچیدگی به صورت n*lgn درمی‌آید. الگوریتم های مرتب سازی زیر وهله‌هایی از این موضوع را به شما نمایش می‌دهند.

چرا مرتب‌سازی مهم است؟

مرتب‌سازی یکی از ساده‌ترین کاربردهای O بزرگ است که هر برنامه‌نویس باید یک درک مقدماتی از آن داشته باشد. اغلب زبان‌های برنامه‌نویسی دارای الگوریتم های مرتب سازی داخلی هستند؛ اما همچنان درک طرز کار مرتب‌سازی حائز اهمیت است. در ادامه دلایل اهمیت این موضوع را توضیح داده‌ایم.

موارد استفاده مهم زیادی دارد

بدیهی است که بزرگ‌ترین استفاده از مرتب‌سازی برای افزایش سرعت جستجوی یک آرایه از (O(n به (O(lgn است که بهبود بزرگی به حساب می‌آید. این نوع جستجو به نام جستجوی باینری یا دودویی نیز نامیده می‌شود. ضمناً ارائه داده‌ها به کاربر در یک قالب خاص (مثلاً از اندازه بزرگ به کوچک) نیز امری رایج است. همچنین مواردی از دستکاری داده‌ها بر مبنای موقعیتشان در یک فهرست مرتب (مانند نمایش مطالب منتشرشده اخیر در یک بلاگ) نیز امری متداول محسوب می‌شود.

در مصاحبه‌های فنی و شغلی پرسیده می‌شود

الگوریتم های مرتب سازی می‌توانند زمان اجراهای بسیار متفاوتی بر مبنای داده‌هایی که روی آن اجرا می‌شوند داشته باشند. با این که بسیاری از الگوریتم های مرتب سازی موجود روی اغلب داده‌ها به خوبی کار می‌کنند؛ اما باید دانست که کدام الگوریتم‌های مختلف برای کاربردهای خاص مناسب‌تر هستند. این که صرفاً از الگوریتم مرتب‌سازی استاندارد یک زبان برنامه‌نویسی استفاده کنیم، امری چندان مناسبی تلقی نمی‌شود.

نکته آخر و احتمالاً مهم‌ترین نکته در مورد اهمیت یادگیری الگوریتم های مرتب سازی این است که این امر به شما کمک می‌کند تا درکی از اهمیت O بزرگ بیابید و با رویکرد‌های حل مسئله به روشی هوشمندانه‌تر از راه‌حل‌های کورکورانه (brute-force) آشنا شوید.

یک الگوریتم مرتب‌سازی چگونه و با چه پیچیدگی زمانی کدنویسی می‌شود؟

در ابتدا باید اعلام کنیم که در مثال‌های ارائه شده در این مقاله صرفاً بر روی پیچیدگی زمانی الگوریتم‌ها متمرکز شده‌ایم و پیچیدگی فضایی الگوریتم‌ها در نظر گرفته نشده است.

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

همچنین معیار بهتر برای این الگوریتم‌ها این است که تعداد سوئیچ‌ها و مقایسه‌هایی که انجام می‌دهند را در نظر بگیریم و نه صرفاً زمان اجرا روی یک ماشین خاص. برای سهولت، شهود و شفافیت بیشتر ما صرفاً زمان اجرا را بررسی می‌کنیم. در آزمون‌های ما RAM هرگز کامل پر نشد و تأثیر عملیات IO دیسک نیز بر روی زمان اجرا محاسبه نشده است.

الگوریتم‌ها

در این بخش الگوریتم‌های مختلف مرتب‌سازی و پیچیدگی زمانی هر کدام مورد بررسی قرار گرفته‌اند.

مرتب‌سازی حبابی

مرتب‌سازی حبابی یا Bubble Sort یکی از ساده‌ترین انواع الگوریتم های مرتب سازی محسوب می‌شود.

خصوصیات

• پیچیدگی زمان بدترین حالت و حالت متوسط این الگوریتم برابر با (ϴ(n² است.
• دقت کنید که حلقه‌های تو در تو به طور کلی زمان اجرای (ϴ(n² دارند.
• پیچیدگی زمانی بهترین حالت آن نیز برابر با (ϴ(n است.

توضیح الگوریتم

در الگوریتم مرتب‌سازی حبابی، با بررسی هر عنصر با عنصر مجاورش، کل یک لیست مورد بررسی قرار می‌گیرد. عناصر مجاور در صورتی که مرتب نباشند جایشان را با هم عوض می‌کنند. این فرایند تا زمانی که همه عناصر با هم تعویض شده باشند تکرار می‌شود. برای بهینه‌سازی این الگوریتم می‌توانید هر بار روی n-i آیتم چرخه را تعریف کنید که i تعداد تکرارهای قبلاً انجام یافته است. دلیل این مسئله آن است که پس از نخستین جابجایی مطمئن می‌شویم که کوچک‌ترین عدد در بالای لیست قرار گرفته است و یا در روش مرتب‌سازی نزولی بزرگ‌ترین عدد در ته لیست جای گرفته است. بنابراین تنها باید اندیس‌های زیر (یا بالای) آن را بررسی کنیم.

مرتب‌سازی حبابی حتی در حالت بهینه خود نیز روی مجموعه داده‌های بزرگ کاملاً کُند است. می‌توان آن را طوری برنامه‌نویسی کرد که در صورت عدم انجام هیچ گونه جابجایی return صورت گیرد، یعنی مشخص می‌شود که داده‌ها مرتب هستند؛ اما این وضعیت تنها در مواردی مفید است که یک آرایه کاملاً مرتب شده در اختیار داشته باشیم. ما برای روشن‌تر بودن روش کار، این بهینه‌سازی را در کد زیر اعمال نکرده‌ایم بک دلیل دیگر آن است که این خصوصیت در مرتب‌سازی درجی نسبت به مرتب‌سازی حبابی بهتر پیاده‌سازی می‌شود.

1def bubble_sort(coll)
2    for i in 0...(coll.length - 1) do
3        for j in (i+1)...coll.length do
4            if coll[i] > coll[j] 
5                coll[i], coll[j] = coll[j], coll[i]
6            end
7        end
8    end
9    coll
10end

مرتب‌سازی درجی

«مرتب‌سازی درجی» (Insertion Sort) یکی دیگر از روش‌های مرتب‌سازی داده‌ها است.

خصوصیات

• پیچیدگی زمانی بدترین حالت و حالت متوسط این روش برابر با (ϴ(n² است.
• پیچیدگی زمانی بهترین حالت برابر با (ϴ(n است.
• سناریوی بهترین حالت زمانی اتفاق می‌افتد که لیست از قبل مرتب‌سازی شده باشد (یا بسیار به این حالت نزدیک باشد).

توضیح الگوریتم

فرض کنید مجموعه شما به چند بخش تقسیم شده باشد. اندیسی که در انتهای چپ قرار دارد (یعنی اندیس 0) در واقعه یک «آرایه مرتب» از یک عنصر محسوب می‌شود. بقیه آرایه همچنان نامرتب هستند. ما می‌توانیم در بخش راست که نامرتب است یک به یک عناصر را بررسی کرده و آن عنصر را مستقیماً در سمت مرتب درج کنیم و به این ترتیب آن بخش یک واحد رشد می‌یابد. زمانی که به انتهای آرایه برسیم؛ کل سمت چپ (یعنی کل آرایه) مرتب‌سازی شده است.

دلیل این که پیچیدگی این روش برابر با (ϴ(n² است، این است که برای هر اندیس در بخش مرتب نشده باید کل سمت مرتب شده را بگردیم تا مکان مناسب درج آن آیتم را پیدا کنیم. علاوه بر آن باید همه عناصری که در مسیر قرار دارند را به روشی انتقال دهیم که فضا برای درج آن آیتم باز شود و این مسئله نیز پر هزینه است.

لازم به ذکر است که هم به تعداد مقایسه‌ها و هم تعداد جابجایی‌ها توجه داشته باشیم. برای هر اندیس در سمت راست آرایه، باید از 1 تا n در سمت چپ آن بگردیم تا موقعیت مناسب درج آیتم را پیدا کنیم. مجموع 1 تا n یک بزرگی برابر با (ϴ(n^2 خواهد داشت.

نامتغیر حلقه

این الگوریتم را از طریق یک «نامتغیر حلقه» (loop invariant) می‌توانیم ارزیابی کنیم. یک نامتغیر حلقه روشی برای اثبات درستی یک الگوریتم است که وظایفی تکراری را اجرا می‌کند. برای انجام صحیح این کار باید یک گزاره نامتغیر حلقه (LI) را نمایش دهیم که برای موارد زیر «درست» باشد:

• مقداردهی اولیه – گزاره LI شما پیش از نخستین اجرای حلقه True باشد.
• نگهداری – گزاره LI شما در سراسر مدت اجرای متعاقب حلقه True بماند.
• خاتمه – گزاره LI شما در انتهای برنامه روشی در اختیار شما قرار می‌دهد که نشان بدهد الگوریتم شما صحیح است.

یک نامتغیر حلقه به این صورت تعریف می‌شود. چنان که در کتاب «مقدمه‌ای بر الگوریتم‌ها» بیان شده است:
در آغاز هر تکرار حلقه، زیرآرایه از 0 تا j-1 (انحصاری) شامل عناصری است که از ابتدا در آن محدوده اندیس بوده‌اند؛ اما اینک مرتب‌سازی شده‌اند.

• مقداردهی اولیه – از آنجا که در انتهای سمت چپ آرایه یک عنصر منفرد (یعنی 0 تا j=1-1=0) قرار دارد، برحسب تعریف، مرتب‌سازی شده محسوب می‌شود.
• نگهداری – هر بار که حلقه تکرار می‌شود، یک آیتم از سمت نامرتب برداشته و در سمت مرتب در موقعیت صحیح قرار می‌دهیم. در این حالت اندیس‌ها به‌روزرسانی می‌شوند و به این ترتیب می‌توانیم بدانیم که از کجا باید آرایه را تقسیم کنیم. سمت مرتب یک واحد بزرگ‌تر می‌شود و همچنان مرتب می‌ماند. پیش از حلقه و پس از حلقه، زیرآرایه از 0 تا j-1 مرتب است؛ اما انتهای حلقه یعنی j یک واحد بزرگ‌تر از قبل است.
• خاتمه – حلقه شما زمانی پایان می‌گیرد که j برابر با طول آرایه منهای 1 باشد. بدین ترتیب می‌دانیم که آرایه از 0 تا «طول آرایه منهای 1» به طور انحصاری مرتب‌سازی شده است. بدین ترتیب همه اندیس‌های آرایه مرتب‌سازی شده‌اند و این بدان معنی است که کل آرایه مرتب است.

همان طور که در ادامه خواهید دید؛ با این که در اغلب موارد مرتب‌سازی درجی بسیار کند است؛ اما در زمان مرتب‌سازی داده‌های تقریباً مرتب، مانند یک قهرمان ظاهر می‌شود!

1def insertion_sort!(coll)
2    for j in 1...coll.length do
3        key = coll[j]
4        # insert coll[j] into sorted sequence coll[0..j-1]
5        i = j-1
6        while i >= 0 && coll[i] > key
7            coll[i+1] = coll[i]
8            i -= 1
9        end
10        coll[i+1] = key
11    end
12    coll
13end

مرتب‌سازی ادغامی

مرتب‌سازی ادغامی یا Merge Sort نیز یکی دیگر از انواع الگوریتم های مرتب سازی است که در ادامه مورد بررسی قرار می‌دهیم.

فیلم آموزش طراحی الگوریتم – مرور و تست کنکور ارشد در فرادرس

کلیک کنید

خصوصیات

پیچیدگی زمانی بدترین حالت، حالت متوسط و بهترین حالت برابر با (ϴ(n*lgn است.

توضیح الگوریتم

در این الگوریتم از رویکرد «تقسیم و حل» (Divide and conquer) استفاده می‌کنیم. مسئله را به صورت پیوسته به دو نیمه تقسیم می‌کنیم تا به آرایه‌ای با اندازه 1 برسیم.

مسئله مرتب‌سازی را هنگامی اندازه برابر با یک است، حل می‌کنیم؛ اما این مسئله خود حل شده است، زیرا آرایه با اندازه 1 با هر تعریفی، یک آرایه مرتب محسوب می‌شود. بدین ترتیب نخستین بازگشتی از تابع merge_sort به دست می‌آید. این بازگشتی همواره یک آرایه مرتب خواهد بود چه طول آن 1 باشد و یا به صورت یک آرایه مرتب ادغام شده باشد و امکان ادامه کار الگوریتم با حفظ وضعیت مرتب‌سازی شده آرایه‌ها در زمان ترکیب کردنشان را فراهم می‌کند.

در ادامه دو نیمه کوچک‌تر که هر دو اندازه‌ای برابر با 1 دارند (و مرتب‌سازی شده‌اند) را با هم ترکیب می‌کنیم تا یک آرایه مرتب شده با اندازه 2 به دست آید.

اگر در رابطه بازگشتی به یک لایه بالاتر برویم، 2 آرایه با اندازه 2 خواهیم داشت که مرتب هستند. با ترکیب کردن آن‌ها با هم یک آرایه مرتب‌سازی شده جدید با طول 4 به دست می‌آوریم و بدین ترتیب کل آرایه مرتب‌سازی می‌شود.

ادغام نامتغیر حلقه

با توجه به تعریف رسمی نامتغیر حلقه به مراحل زیر نیاز داریم.

گزاره

در ابتدای شروع به کار حلقه، merged_arr شامل کوچک‌ترین عناصر (i+j) از آرایه‌های left و right خواهد بود که به صورت مرتب‌سازی شده هستند. [left[i و [right[j شامل کوچک‌ترین اعداد در آرایه‌های متناظر خود برای اندیس‌های بزرگ‌تر از i و j متناظر خود خواهند بود.

مقداردهی اولیه

merged_arr خالی و I + j = 0 است. left و right آرایه‌های مرتب هستند و از این رو مقادیر عناصر 0 هر دو آن‌ها در کل آرایه‌ها، کوچک‌ترین عناصر خواهند بود.

نگهداری

عدد کوچک‌تر در میان دو عدد [left[i و [right[j به انتهای merged_arr الحاق می‌شود. از آنجا که هر دو آرایه به صورت مرتب‌سازی شده هستند و i و j هر دو از صفر افزایش یافته‌اند، مطمئن هستیم که هر تکرار حلقه while تنها اعدادی را بررسی می‌کند که به آن الحاق یافته‌اند و بزرگ‌تر یا مساوی اعداد الحاق شده قبلی به merged_arr و کوچک‌تر یا مساوی اعداد اندیس‌های بالاتر باقیمانده در left و right هستند. بدین ترتیب مطمئن خواهیم بود که شرایط مرتب‌سازی شده merged_arr حفظ می‌شود.

زمانی که یک عنصر به merged_arr از سمت left الحاق می‌شود، i به میزان 1 واحد افزایش می‌یابد و زمانی که یک عنصر از سمت right به merged_arr الحاق می‌شود نیز j 1 واحد افزایش می‌یابد. بدین ترتیب مطمئن خواهیم بود که merged_arr.length برابر با i+j است و مقادیر merged_arr به صورت مرتب هستند و دو عدد بعدی [left[i و [right[j بزرگ‌تر یا مساوی همه اعداد موجود در merged_arr و کمتر یا مساوی همه مقادیر موجود در آرایه‌های متناظر خود نیز هستند. یعنی این دو عنصر کوچک‌ترین مقادیر موجود در آرایه‌های خود هستند که قبلاً در merged_arr قرار نگرفته‌اند.

خاتمه

این حلقه زمانی متوقف می‌شود که آرایه خالی شود. می‌دانیم که در این مرحله merged_arr به صورت مرتب درآمده است و همه مقادیر آرایه بسط یافته و همه مقادیر آرایه دیگر تا اندیس i و j مرتب است. مرحله خاتمه عالی است؛ اما نیازمند اندکی پاک‌سازی است. شما باید بخش باقیمانده آرایه را با مقادیر بر جای مانده در انتهای merged_arr پر کنید. بدین منظور کافی است آن‌ها را در انتهای آرایه قرار دهید زیرا آرایه با مقادیر بر جای مانده مرتب است و کمترین مقادیر تعیین شده بزرگ‌تر یا مساوی بزرگ‌ترین مقدار در آرایه دیگر هستند.

دقت کنید که در برخی موارد دو «sentinel» در انتهای left و right قرار می‌گیرند و مقدار نامتناهی ایجاد می‌کنند. در این حالت حلقه while با یک حلقه for عوض می‌شود که به میزان left.length + right.length – 2 دفعه اجرا می‌شود به طوری که تنها دو مقدار sentinel نامتناهی باقی بمانند. در Ruby می‌توانید نامتناهی را با Float::INFINITY نشان دهید. در پایتون این وضعیت با ("float("inf، در جاوا اسکریپت با Infinity و در جاوا با Double.POSITIVE_INFINITY نمایش می‌یابد.

کد

1def merge_sort(coll)
2    len = coll.length
3    return coll if len == 1
4    left = coll[0, len / 2]
5    right = coll[len / 2, len]
6    left_sorted = merge_sort(left)
7    right_sorted = merge_sort(right)
8    merge(left_sorted, right_sorted)
9end
10
11def merge(left, right)
12    merged_arr = []
13    i, j = 0, 0
14    while i < left.length && j < right.length
15        #puts "Comparing lhs #{left[i]} to rhs #{right[j]}"
16        if left[i] <= right[j]
17            #puts "Adding lhs #{left[i]}"
18            merged_arr << left[i]
19            i += 1
20        else
21            #puts "Adding rhs #{right[j]}"
22            merged_arr << right[j]
23            j += 1
24        end
25    end
26    merged_arr.concat right[j, right.length] if i == left.length
27    merged_arr.concat left[i, left.length] if j == right.length
28    #puts merged_arr.to_s
29    merged_arr
30end

مرتب‌سازی سریع

مرتب‌سازی سریع با Quick Sort یکی از الگوریتم‌های دیگر مرتب‌سازی محسوب می‌شود.

فیلم آموزش طراحی الگوریتم در فرادرس

کلیک کنید

خصوصیات

• پیچیدگی زمانی بدترین حالت و حالت متوسط برابر با (ϴ(n*lgn است.
• پیچیدگی زمانی بدترین حالت (زمانی که تقریباً مرتب باشد) برابر با (ϴ(n² است.
• اگر به کد زیر نگاه کنید می‌بینید که یک «محور» (pivot) وجود دارد. می‌توانید ببینید در حالت مرتب‌سازی شده،
• مسئله به جای n/2 و n/2، به دو بخش با اندازه‌های n-1 و 1 تقسیم می‌شود. برای یک آرایه تصادفی شده این احتمال بیشتر است که محور، مقداری نزدیک به مقدار میانه باشد.

توضیح الگوریتم

این الگوریتم نیز دارای رویکرد تقسیم و حل است که در ادامه آن را توضیح می‌دهیم.

تقسیم

یک نقطه محوری در اندیس آخر آرایه انتخاب می‌کنیم. چرخه‌ای روی آرایه تعریف کرده و مقادیری که در سمت نادرست مقدار محور هستند را جا به جا می‌کنیم تا این که مقادیر بزرگ‌تر یا مساوی محور در سمت راست اندیس و همه مقادیر کوچک‌تر در سمت چپ اندیس قرار گیرند. آرایه را به وسیله آن اندیس تقسیم می‌کنیم تا دو زیرمسئله کوچک‌تر ایجاد شود.

حل

زمانی که اندازه‌ها به قدر کافی کوچک باشند (یعنی 1 یا 2)، این روش تقسیم موجب می‌شود که زیرمجموعه‌ها مرتب‌سازی شوند. گروه‌بندی اعداد برحسب بزرگ یا کوچک‌تر بودن از محور در یک مقیاس بزرگ تضمین می‌کند که الگوریتم روی آرایه با مقیاس کوچک‌تر 2 (که در واقع موجب مرتب‌سازی آرایه می‌شود) در مکانی از آرایه اجرا می‌شود که موجب مرتب‌سازی همه آرایه خواهد شد و محدود به داده‌های مرتب‌سازی محلی نخواهد شد.

ترکیب

همانند مرحله حل در الگوریتم مرتب‌سازی ادغامی که برحسب آزمون و خطا بود، از آنجا که همه کار در مرحله ترکیب انجام می‌گیرد، مرحله تقسیم مرتب‌سازی سریع نیز صوری است، زیرا همه کار در مرحله تقسیم صورت گرفته است. پس از این که آرایه به مجموعه‌های 1 و 2 تقسیم شد، مرتب محسوب می‌شود. این الگوریتم زمانی که اندازه زیرآرایه‌ها مساوی یا کمتر از صفر شود، متوقف می‌شود.

نامتغیر حلقه افراز

ابتدا به کدی که در ادامه ارائه شده است، توجه کنید.

گزاره

مقادیر arr از مقدار آرگومان اصلی lo تا مقدار کنونی lo همگی کمتر یا برابر با مقدار محور هستند. مقادیر arr از مقدار آرگومان اصلی hi تا مقدار کنونی hi همگی بزرگ‌تر یا مساوی مقدار محور هستند.

مقداردهی اولیه

lo و hi طوری مقداردهی اولیه می‌شوند که به ترتیب کمتر یا بزرگ‌تر از مقادیر اولیه‌شان باشند. شما در خارج از آرایه و بدون هیچ ارتباطی با مقادیر، به طور صوری الزاماتی که به مقادیر arr مربوط هستند را چنان که در LI ذکر شده‌اند، تأمین می‌کنید.

نگهداری

پس از یک بار اجرای حلقه، مقدار اندیس lo طوری افزایش می‌یابد که از همه مقادیر اندیس کمتر از محور رد می‌شود. زمانی که حلقه در نهایت متوقف می‌شود، تضمین شده است که lo در مقدار اندیسی ثابت شده است که بزرگ‌تر یا مساوی مقدار محور است و همه مقادیر سمت چپ آن کمتر از مقدار محور هستند. همچنین در صورتی که تا سمت چپ lo جا به جا شده باشند برابر با آن هستند. ‘hi’ نیز به روش مشابهی کاهش یافته است و در اندیسی متوقف شده است که مقدار آن کمتر یا مساوی مقدار محور است و تضمین می‌شود که همه مقادیر سمت راست ‘hi’ بزرگ‌تر از مقدار محور هستند. در صورتی که تا سمت راست hi جا به جا شده باشند، می‌توانند با آن برابر باشند.

اگر hi > lo باشد آن‌ها را تعویض می‌کنیم، زیرا می‌دانیم که حلقه‌های داخلی روی مقادیری متوقف می‌شوند که باید با سمت بیرونی یا میانی آرایه تقسیم شده به وسیله مقدار محوری مرتبط باشند و ما هنوز به مقدار میانی نرسیده‌ایم. این بدان معنی است که مقدار جدید برای [arr[lo باید الزامات مورد نیاز حلقه [arr[hi را تأمین کرده باشد تا متوقف شود، یعنی کمتر مساوی pivot باشد و مقدار جدید برای [arr[hi نیز باید الزامات مورد نیاز برای حلقه [arr[lo را تأمین کند و یا در صورت عبور کردن از حلقه، پایین‌تر از مقدار محور باشند و یا اگر از نقطه‌ای که قبلاً در اندیس hi بوده است تعویض شده‌اند کمتر مساوی مقدار محور باشد. به بیان دیگر همه آن‌ها باید کمتر یا مساوی مقدار محور باشند. به طور عکس تضمین می‌شود که همه مقادیر در اندیس ‘hi’ و بالاتر، بزرگ‌تر از مقدار محور یا مساوی یا آن هستند.

خاتمه

از آنجا که Lo >= hi است، می‌دانیم که به نقطه‌ای در آرایه می‌رسیم که به صورت عددی به وسیله محور تقسیم شده است. ما مقدار بزرگ‌تر را از میان دو اندیس بازگشت می‌دهیم و امکان ایجاد زیرمجموعه‌هایی از آرایه را ایجاد می‌کنیم که همه مقادیر زیر partition_index – 1 کمتر یا مساوی محور باشند و همه مقادیر بالاتر از partition بزرگ‌تر یا مساوی محور باشند. ضمناً با تقسیم مجدد آرایه به روشی مشابه مرتب‌سازی سریع، از ایجاد یک حلقه نامتناهی ممانعت می‌کنیم و یک اندیس پارتیشن برای ایجاد زیرمجموعه خالی و آرایه اصلی ایجاد می‌کنیم. زمانی که زیرآرایه به اندازه 1 یا 2 برسد، partition موجب بازگشت یک بخش از زیرآرایه مرتب می‌شود که در موقعیت صحیحی نسبت به کل آرایه نیز قرار دارد.

کد

1def quicksort!(coll, lo = 0, hi = nil)
2    hi = coll.length - 1 if hi.nil?
3    if lo < hi
4        partition_index = partition(coll, lo, hi)
5        quicksort!(coll, lo, partition_index - 1)
6        quicksort!(coll, partition_index, hi)
7    end
8end
9
10#Hoar Partition
11def partition(arr, lo, hi)
12    pivot = arr[hi]
13    lo -= 1
14    hi += 1
15    loop do
16        loop do
17            lo += 1
18            break if arr[lo] >= pivot
19        end
20
21        loop do
22            hi -= 1
23            break if arr[hi] <= pivot
24        end
25        return lo if lo >= hi
26        arr[lo], arr[hi] = arr[hi], arr[lo]
27    end
28end

پیچیدگی زمان اجرای الگوریتم روی داده‌های تصادفی و تقریباً مرتب‌سازی شده

1numbers = []
21000000.times do 
3    numbers << r.rand(500000)
4end

خروجی اعداد تصادفی

1Bubble sort (1 million numbers): 33323.8596392 s, (555.4 mins)
2
3Insertion sort (1 million numbers): 13213.5302226 s, (220.2 mins)
4
5Merge sort (1 million numbers): 2.0483875 s
6
7Quick sort (1 million numbers): 3.6877069 s
8
9Ruby's native #sort (1 million numbers): 1.0330547 s, (a very optimized Quicksort algorithm)

در اغلب موارد مجبور هستیم مجموعه‌ای را که قبلاً تا حدود زیادی مرتب‌سازی شده، مرتب‌سازی کنیم. در ادامه عملکرد الگوریتم‌های مختلف را در این زمینه مشاهده می‌کنید.

1Ruby's native #sort (mostly sorted 1 million nums): 0.6229407 s (a very optimized Quicksort algorithm)
2
3Merge sort (mostly sorted 1 million nums): 1.5681328 s 
4
5Insertion sort (mostly sorted 1 million nums): 0.1712918 s

اگر می‌دانید که مرتباً باید یک مجموعه را که تقریباً به طور کامل مرتب‌سازی شده، مجدداً مرتب‌سازی کنید و می‌خواهید سریع‌ترین زمان مرتب‌سازی ممکن را داشته باشند، الگوریتم مرتب‌سازی درجی بهترین گزینه است و حتی مرتب‌سازی داخلی روبی که کاملاً بهینه‌سازی شده است را با ضریبی در حد 3 برابر شکست می‌دهد.

اجتناب از مرتب‌سازی سریع در بدترین حالت

زمانی که مرتب‌سازی سریع روی لیست تقریباً مرتب‌سازی شده اجرا می‌شود موجب از کار افتادن برنامه می‌شود و باید اندازه مجموعه داده از 1 میلیون تا حدود 15000 کاهش یابد.

1Quick sort (mostly sorted 15670 nums): 3.8133098 s

در این مرحله پیچیدگی زمان اجرای این 15000 عنصر مرتب‌سازی شده برابر با مرتب‌سازی سریعی است که روی 1 میلیون عنصر تصادفی اجرا می‌شود و با این که تعداد بازگشت‌های مرتب‌سازی سریع کمتر است، تعداد حلقه‌هایی که در متد partition اجرا می‌شوند بسیار بیشتر است.

همان طور که توضیح دادیم، دلیل وقوع این حالت آن است که نقطه محوری در انتهای آرایه قرار دارد و از این رو هر عنصر منفرد دیگر در arr کمتر از مقدار محور است. بدین ترتیب به جای ایجاد دو زیرمسئله برای رسیدن به زمان اجرایی برابر با nlgn، در عمل دو زیرمسئله ایجاد کرده‌ایم که اندازه‌های 1 و n-1 دارند. مجموع 1 تا n، پیچیدگی زمانی (ϴ(n^2 را تولید می‌کند. برای نمونه می‌توانید عمل جمع زدن اعداد 1 تا 10 را در نظر بگیرید. حاصل این جمع به صورت زیر است:

 (10 + 1) * (10 / 2) = 55

اگر 10 را با n جایگزین کنیم مجموعاً  تعداد حالت‌ها به صورت زیر است:

(n + 1) * (n/2) = (n^2)/2 + n/2

اگر ضرایب و جمله‌های با مرتبه پایین را حذف کنیم به n^2 می‌رسیم.

برای حل این مسئله با زمان اجرای (ϴ(n² برای یک لیست تقریباً مرتب‌سازی شده می‌توانیم در مورد روش انتخاب نقطه محور، هوشمندانه‌تر عمل کنیم. اگر optimize_pivot را برای انتخاب نقطه محوری اجرا کنیم، در این صوت مقدار میانه بین مقادیر اندیس پایین، بالا و میانه را به عنوان اندیس pivot انتخاب می‌کنیم. سپس آن مقدار را با [arr[hi تعویض می‌کنیم و به استفاده از hi به عنوان محور ادامه می‌دهیم. اگر آرایه قبلاً مرتب‌سازی شده باشد اینک از مقدار میانه لیست به جای یک انتها استفاده می‌کنیم و می‌توانیم به زمان اجرای (ϴ(n * lgn روی یک لیست مرتب‌سازی شده برسیم، زیرا یک بار دیگر مسئله را به جای تفریق 1 از اندازه آرایه، به دو نیمه تقسیم کرده‌ایم.

کد بهتر برای مرتب‌سازی سریع

1def quicksort_opt!(coll, lo = 0, hi = nil)
2    hi = coll.length - 1 if hi.nil?
3    if lo < hi
4        partition_index = partition_opt(coll, lo, hi)
5        quicksort_opt!(coll, lo, partition_index - 1)
6        quicksort_opt!(coll, partition_index, hi)
7    end
8end
9
10def partition_opt(arr, lo, hi)
11     optimize_pivot(arr, lo, hi)
12     pivot = arr[hi]
13     lo -= 1
14     hi += 1
15     loop do
16         loop do
17             lo += 1
18             break if arr[lo] >= pivot
19         end
20 
21         loop do
22             hi -= 1
23             break if arr[hi] <= pivot
24         end
25         return lo if lo >= hi
26         arr[lo], arr[hi] = arr[hi], arr[lo]
27     end
28end
29
30def optimize_pivot(arr, lo, hi)
31    mid = (lo + hi) / 2
32    arr[lo], arr[mid] = arr[mid], arr[lo] if arr[mid] < arr[lo]
33    arr[lo], arr[hi] = arr[hi], arr[lo] if arr[hi] < arr[lo]
34    arr[mid], arr[hi] = arr[hi], arr[mid] if arr[mid] < arr[hi]
35end

در این بخش معیار عملکرد ثانویه برای همه الگوریتم با شمول مرتب‌سازی بهینه ارائه شده است:

1Ruby's native sort (1 million numbers): 1.1003078 s
2Merge sort (1 million nums): 2.1523891 s
3Quick sort (1 million nums): 3.8681517 s
4Quick sort optimized (1 million nums): 3.8711199 s
5Ruby sort (mostly sorted 1 million nums): 0.5628704 s
6Merge sort (mostly sorted 1 million nums): 1.453362 s
7Optimized quicksort (mostly sorted 1 million nums): 2.6978179 s
8Insertion sort (mostly sorted 1 million nums): 0.1951487 s