فرادرس
الگوریتم بروکا (Boruvka’s Algorithm) — راهنمای کاربردی
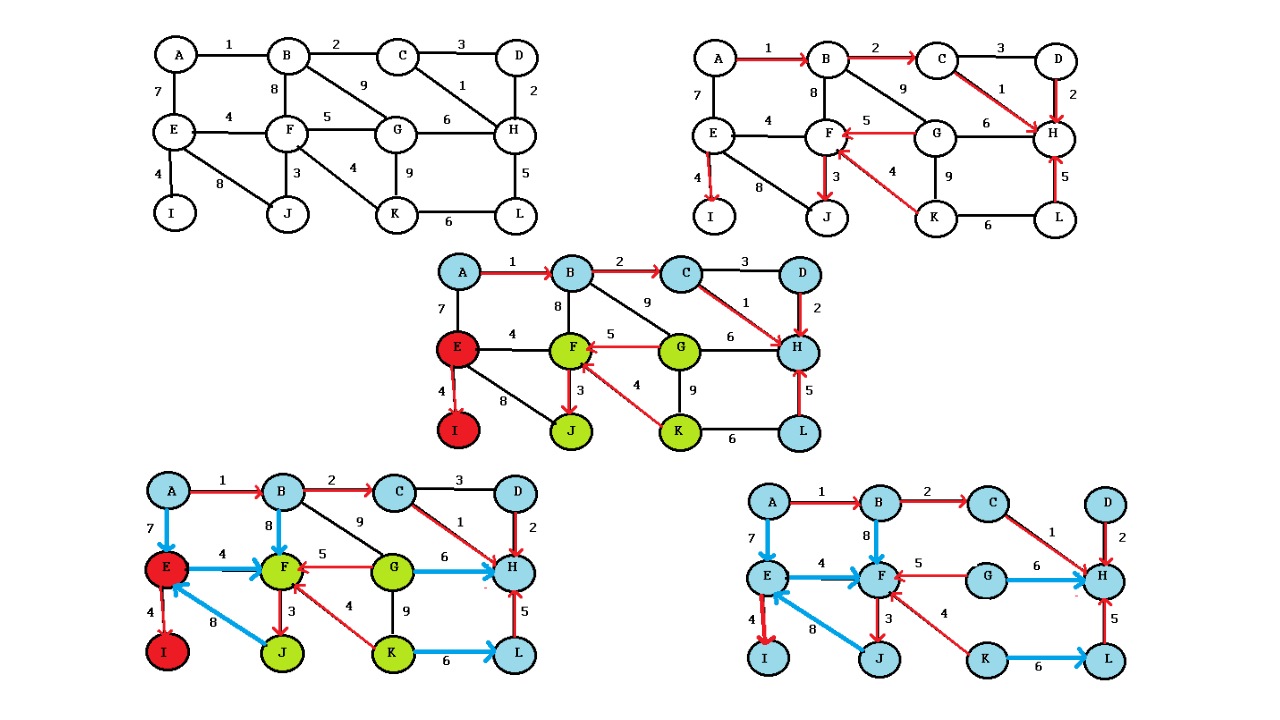
در این مطلب، «الگوریتم بروکا» (Boruvka’s Algorithm) مورد بررسی قرار گرفته و پیاده‌سازی آن در زبان‌های برنامه‌نویسی C++/C و پایتون انجام شده است. الگوریتم بروکا نیز مانند «الگوریتم پریم» (Prim's Algorithm) و «الگوریتم کراسکال» (Kruskal Algorithm)، یک «الگوریتم حریصانه» (Greedy Algorithm) است.
الگوریتم بروکا
در زیر، الگوریتم بروکا به طور کامل ارائه شده است.
- ورودی، یک گراف متصل، وزن‌دار و غیر جهت‌دار است.
- همه راس‌ها را به عنوان عنصر‌های مجزا مقداردهی کن.
- درخت پوشای کمینه را به عنوان empty مقداردهی اولیه کن.
- در حالیکه بیش از یک عنصر وجود دارد، برای هر عنصر، اقدامات زیر را انجام بده:
- یالی با نزدیک‌ترین وزن که این عنصر را به سایر عناصر متصل می‌کند، پیدا کن.
- این نزدیک یال را در صورتی که تاکنون به درخت پوشای کمینه اضافه نشده، اضافه کن.
- درخت پوشای کمینه را بازگردان.
در ادامه، ایده نهفته در پس الگوریتم بروکا، همراه با مثال نمایش داده شده است. شایان ذکر است که ایده این الگوریتم، مانند الگوریتم «درخت پوشای کمینه» (Minimum Spanning Tree) پریم است. منظور از درخت پوشای کمینه آن است که همه راس‌ها متصل باشند. بنابراین، دور زیرمجموعه غیرمتصل (که در بالا تشریح شده است) از راس‌ها باید متصل باشند تا یک درخت پوشا ساخته شود. همچنین، آن‌ها باید با یال دارای حداقل وزن متصل شوند تا از آن یک درخت پوشای کمینه بسازند. در ادامه، مفهوم این الگوریتم با استفاده از مثالی، بیان می‌شود.
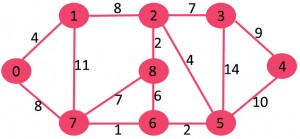
به طور اولیه، MST خالی است. هر راسی یک عنصر مجرد است که با خط آبی در تصویر زیر مشخص شده است.
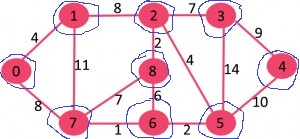
برای هر عنصر، کم‌وزن‌ترین یالی که آن را به دیگر عنصر‌ها متصل می‌کند، یافت می‌شود.
Component Cheapest Edge that connects
it to some other component
{0} 0-1
{1} 0-1
{2} 2-8
{3} 2-3
{4} 3-4
{5} 5-6
{6} 6-7
{7} 6-7
{8} 2-8
سبک‌ترین یال‌ها با رنگ سبز مشخص شده‌اند. اکنون، درخت پوشای کمینه به صورت $${0-1, 2-8, 2-3, 3-4, 5-6, 6-7}$$ است.
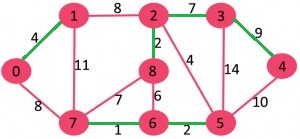
پس از مراحل بالا، عنصر‌ها $${{0,1}, {2,3,4,8}, {5,6,7}}$$ هستند. این عنصر‌ها با دوایر آبی رنگ مشخص شده‌اند.
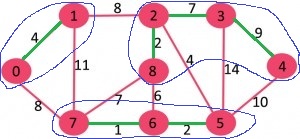
اکنون، مجددا مراحل تکرار می‌شوند. برای هر عنصر، سبک‌ترین یالی که آن را به دیگر عنصر‌ها متصل می‌کند، پیدا می‌شود.
Component Cheapest Edge that connects
it to some other component
{0,1} 1-2 (or 0-7)
{2,3,4,8} 2-5
{5,6,7} 2-5
سبک‌ترین یال‌ها با رنگ سبز مشخص شده‌اند. اکنون، درخت پوشای کمینه به صورت $${0-1, 2-8, 2-3, 3-4, 5-6, 6-7, 1-2, 2-5}$$ است.
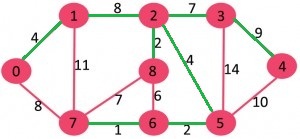
در این گام، تنها یک عنصر {0, 1, 2, 3, 4, 5, 6, 7, 8} وجود دارد که همه یال‌ها را دربر می‌گیرد. با توجه به اینکه تنها یک عنصر باقی مانده است، کار متوقف و درخت پوشای کمینه بازگردانده می‌شود. در ادامه، پیاده‌سازی الگوریتم بروکا در زبان‌های برنامه‌نویسی C++/C و پایتون انجام شده است.
پیاده‌سازی الگوریتم بروکا در C++/C
// Boruvka's algorithm to find Minimum Spanning
// Tree of a given connected, undirected and
// weighted graph
#include <stdio.h>
// a structure to represent a weighted edge in graph
struct Edge
{
int src, dest, weight;
};
// a structure to represent a connected, undirected
// and weighted graph as a collection of edges.
struct Graph
{
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges.
// Since the graph is undirected, the edge
// from src to dest is also edge from dest
// to src. Both are counted as 1 edge here.
Edge* edge;
};
// A structure to represent a subset for union-find
struct subset
{
int parent;
int rank;
};
// Function prototypes for union-find (These functions are defined
// after boruvkaMST() )
int find(struct subset subsets[], int i);
void Union(struct subset subsets[], int x, int y);
// The main function for MST using Boruvka's algorithm
void boruvkaMST(struct Graph* graph)
{
// Get data of given graph
int V = graph->V, E = graph->E;
Edge *edge = graph->edge;
// Allocate memory for creating V subsets.
struct subset *subsets = new subset[V];
// An array to store index of the cheapest edge of
// subset. The stored index for indexing array 'edge[]'
int *cheapest = new int[V];
// Create V subsets with single elements
for (int v = 0; v < V; ++v)
{
subsets[v].parent = v;
subsets[v].rank = 0;
cheapest[v] = -1;
}
// Initially there are V different trees.
// Finally there will be one tree that will be MST
int numTrees = V;
int MSTweight = 0;
// Keep combining components (or sets) until all
// compnentes are not combined into single MST.
while (numTrees > 1)
{
// Everytime initialize cheapest array
for (int v = 0; v < V; ++v)
{
cheapest[v] = -1;
}
// Traverse through all edges and update
// cheapest of every component
for (int i=0; i<E; i++)
{
// Find components (or sets) of two corners
// of current edge
int set1 = find(subsets, edge[i].src);
int set2 = find(subsets, edge[i].dest);
// If two corners of current edge belong to
// same set, ignore current edge
if (set1 == set2)
continue;
// Else check if current edge is closer to previous
// cheapest edges of set1 and set2
else
{
if (cheapest[set1] == -1 ||
edge[cheapest[set1]].weight > edge[i].weight)
cheapest[set1] = i;
if (cheapest[set2] == -1 ||
edge[cheapest[set2]].weight > edge[i].weight)
cheapest[set2] = i;
}
}
// Consider the above picked cheapest edges and add them
// to MST
for (int i=0; i<V; i++)
{
// Check if cheapest for current set exists
if (cheapest[i] != -1)
{
int set1 = find(subsets, edge[cheapest[i]].src);
int set2 = find(subsets, edge[cheapest[i]].dest);
if (set1 == set2)
continue;
MSTweight += edge[cheapest[i]].weight;
printf("Edge %d-%d included in MST\n",
edge[cheapest[i]].src, edge[cheapest[i]].dest);
// Do a union of set1 and set2 and decrease number
// of trees
Union(subsets, set1, set2);
numTrees--;
}
}
}
printf("Weight of MST is %d\n", MSTweight);
return;
}
// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E)
{
Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[E];
return graph;
}
// A utility function to find set of an element i
// (uses path compression technique)
int find(struct subset subsets[], int i)
{
// find root and make root as parent of i
// (path compression)
if (subsets[i].parent != i)
subsets[i].parent =
find(subsets, subsets[i].parent);
return subsets[i].parent;
}
// A function that does union of two sets of x and y
// (uses union by rank)
void Union(struct subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// Attach smaller rank tree under root of high
// rank tree (Union by Rank)
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
// If ranks are same, then make one as root and
// increment its rank by one
else
{
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// Driver program to test above functions
int main()
{
/* Let us create following weighted graph
10
0--------1
| \ |
6| 5\ |15
| \ |
2--------3
4 */
int V = 4; // Number of vertices in graph
int E = 5; // Number of edges in graph
struct Graph* graph = createGraph(V, E);
// add edge 0-1
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = 10;
// add edge 0-2
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 6;
// add edge 0-3
graph->edge[2].src = 0;
graph->edge[2].dest = 3;
graph->edge[2].weight = 5;
// add edge 1-3
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 15;
// add edge 2-3
graph->edge[4].src = 2;
graph->edge[4].dest = 3;
graph->edge[4].weight = 4;
boruvkaMST(graph);
return 0;
}
// Thanks to Anukul Chand for modifying above code.
پیاده‌سازی الگوریتم بروکا در پایتون
# Boruvka's algorithm to find Minimum Spanning
# Tree of a given connected, undirected and weighted graph
from collections import defaultdict
#Class to represent a graph
class Graph:
def __init__(self,vertices):
self.V= vertices #No. of vertices
self.graph = [] # default dictionary to store graph
# function to add an edge to graph
def addEdge(self,u,v,w):
self.graph.append([u,v,w])
# A utility function to find set of an element i
# (uses path compression technique)
def find(self, parent, i):
if parent[i] == i:
return i
return self.find(parent, parent[i])
# A function that does union of two sets of x and y
# (uses union by rank)
def union(self, parent, rank, x, y):
xroot = self.find(parent, x)
yroot = self.find(parent, y)
# Attach smaller rank tree under root of high rank tree
# (Union by Rank)
if rank[xroot] < rank[yroot]:
parent[xroot] = yroot
elif rank[xroot] > rank[yroot]:
parent[yroot] = xroot
#If ranks are same, then make one as root and increment
# its rank by one
else :
parent[yroot] = xroot
rank[xroot] += 1
# The main function to construct MST using Kruskal's algorithm
def boruvkaMST(self):
parent = []; rank = [];
# An array to store index of the cheapest edge of
# subset. It store [u,v,w] for each component
cheapest =[]
# Initially there are V different trees.
# Finally there will be one tree that will be MST
numTrees = self.V
MSTweight = 0
# Create V subsets with single elements
for node in range(self.V):
parent.append(node)
rank.append(0)
cheapest =[-1] * self.V
# Keep combining components (or sets) until all
# compnentes are not combined into single MST
while numTrees > 1:
# Traverse through all edges and update
# cheapest of every component
for i in range(len(self.graph)):
# Find components (or sets) of two corners
# of current edge
u,v,w = self.graph[i]
set1 = self.find(parent, u)
set2 = self.find(parent ,v)
# If two corners of current edge belong to
# same set, ignore current edge. Else check if
# current edge is closer to previous
# cheapest edges of set1 and set2
if set1 != set2:
if cheapest[set1] == -1 or cheapest[set1][2] > w :
cheapest[set1] = [u,v,w]
if cheapest[set2] == -1 or cheapest[set2][2] > w :
cheapest[set2] = [u,v,w]
# Consider the above picked cheapest edges and add them
# to MST
for node in range(self.V):
#Check if cheapest for current set exists
if cheapest[node] != -1:
u,v,w = cheapest[node]
set1 = self.find(parent, u)
set2 = self.find(parent ,v)
if set1 != set2 :
MSTweight += w
self.union(parent, rank, set1, set2)
print ("Edge %d-%d with weight %d included in MST" % (u,v,w))
numTrees = numTrees - 1
#reset cheapest array
cheapest =[-1] * self.V
print ("Weight of MST is %d" % MSTweight)
g = Graph(4)
g.addEdge(0, 1, 10)
g.addEdge(0, 2, 6)
g.addEdge(0, 3, 5)
g.addEdge(1, 3, 15)
g.addEdge(2, 3, 4)
g.boruvkaMST()
#This code is contributed by Neelam Yadav
خروجی قطعه کد بالا، به صورت زیر است.
Edge 0-3 included in MST Edge 0-1 included in MST Edge 2-3 included in MST Weight of MST is 19
پیچیدگی زمانی الگوریتم بروکا از درجه O(E log V) و در واقع، مشابه با پیچیدگی الگوریتم کراسکال و پریم است. الگوریتم بروکا یکی از قدیمی‌ترین الگوریتم‌های «درخت پوشای کمینه» (Minimum Spanning Tree) است که در سال ۱۹۲۶ میلادی، مدت‌ها پیش از اینکه کامپیوترها حتی وجود داشته باشند، توسط بورکا کشف شده است. این الگوریتم به عنوان روشی برای ساخت شبکه الکتریسیته موثر، معرفی شده بود.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزشهای برنامه نویسی
- آموزش ساختمان داده‌ها
- مجموعه آموزشهای ساختمان داده و طراحی الگوریتم
- رنگ‌آمیزی گراف به روش حریصانه — به زبان ساده
- الگوریتم دایجسترا (Dijkstra) — از صفر تا صد
- الگوریتم پریم — به زبان ساده
- متن کاوی (Text Mining) — به زبان ساده
^^
