پشته (Stack)، صف (Queue) و تجزیه عبارت — ساختار داده و الگوریتم ها

در این نوشته به معرفی برخی از مفاهیم مقدماتی ساختمان داده شامل پشته ، صف و تجزیه عبارت که در اغلب حوزههای محاسبات رایانهای کاربرد دارند، خواهیم پرداخت.
پشته (Stack)
پشته یک نوع داده مجرد (ADT) است که در اکثر زبانهای برنامهنویسی کاربرد رایجی دارد.
دلیل این که این نوع داده، پشته نامیده شده، این است که از نظر ظاهری شبیه پشته است، یعنی به یک دسته کارت روی هم چیده شده یا یک دسته از بشقابهای روی هم شباهت دارد.

یک پشته در دنیای واقعی امکان انجام کارها را تنها از یک سمت فراهم میکند. برای نمونه شما تنها میتوانید کارتها را روی دسته کارتها بگذارید یا از روی آن بردارید. به طور مشابه ADT پشته نیز امکان اجرای عملیاتهای روی داده را تنها در یک سمت ارائه میکند. ما در هر زمان تنها به عناصر فوقانی پشته دسترسی داریم.
این ویژگی باعث میشود که پشته یک ساختار داده LIFO باشد. LIFO اختصاری برای عبارت Last-in-first-out است یعنی ورودی-آخر- خروجی-اول. در اصطلاحشناسی پشته عملیات درج به نام عملیات PUSH نامیده و عملیات حذف به نام POP خوانده میشود.
نمایش پشته
در ادامه نمودار یک پشته و عملیاتهای آن ارائه شده است:
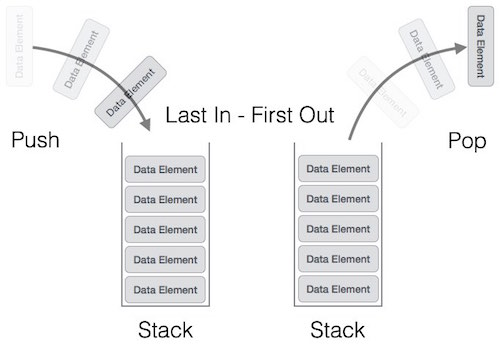
پشته میتواند به وسیله آرایهها، ساختار، اشارهگر و لیست پیوندی نمایش یابد. پشته میتواند دارای اندازه ثابت باشد و یا اندازه آن به طور دینامیک تغییر یابد. در این بخش از نوشته قصد داریم یک پشته را با استفاده از آرایهها پیادهسازی کنیم. چنین پشتهای یک پیادهسازی با اندازه ثابت خواهد داشت.
عملیاتهای ابتدایی
عملیاتهای ابتدایی ممکن است شامل راهاندازی اولیه پشته، استفاده و تخریب آن باشد. علاوه بر آن وقتی عنصری در پشته قرار میگیرد، معمولاً از این دو عملیات ابتدایی استفاده میشود:
- ()Push: ذخیرهسازی یک عنصر در پشته
- ()Pop: حذف (دسترسی به) یک عنصر پشته
برای استفاده بهینه از یک پشته باید وضعیت آن نیز بررسی شود. به این منظور کارکردهای زیر به پشته اضافه شدهاند:
- ()Peek: دریافت بالاترین عنصر پشته بدون حذف آن
- ()isFull: بررسی پر بودن پشته
- ()isEmpty: بررسی خالی بودن پشته
ما باید هر زمان یک اشارهگر به آخرین داده push شده به پشته در اختیار داشته باشیم. از آنجا که این اشارهگر همواره به عنصر فوقانی پشته اشاره میکند، نام آن top تعیین شده است. اشارهگر top بالاترین مقدار پشته را بدون حذف آن به دست میدهد.
در ابتدا باید در مورد رویههایی که برای پشتیبانی از تابعهای پشته مورد نیاز هستند را بشناسیم:
()Peek
الگوریتم تابع ()Peek به صورت زیر است:
begin procedure peek return stack[top] end procedure
پیادهسازی تابع ()Peek در زبان C:
int peek() {
return stack[top];
}
()isFull
الگوریتم تابع ()isFull به صورت زیر است:
begin procedure isfull
if top equals to MAXSIZE
return true
else
return false
endif
end procedure
پیادهسازی تابع ()isFull در زبان C به صورت زیر است:
bool isfull() {
if(top == MAXSIZE)
return true;
else
return false;
}
()isEmpty
الگوریتم تابع ()isEmpty به صورت زیر است:
begin procedure isempty
if top less than 1
return true
else
return false
endif
end procedure
پیادهسازی این تابع در زبان C اندکی متفاوت است. مقدار اولیه top را برابر با 1- در نظر میگیریم، زیرا اندیس در آرایه، از 0 شروع میشود. بنابراین بررسی میکنیم اگر top زیر 0 یا 1- بود، در این صورت میفهمیم که پشته خالی است. بدین ترتیب کد به صورت زیر است:
bool isempty() {
if(top == -1)
return true;
else
return false;
}
عملیات Push
فرایند قرار دادن یک عنصر جدید در پشته به نام عملیات push شناخته میشود. عملیات پوش شامل یک سری از مراحل است:
- گام 1: بررسی کن که پشته پر است یا نه.
- گام 2: اگر پشته پر باشد، اعلام خطا کرده و خارج شو.
- گام 3: اگر پشته پر نبود، مقدار top را یک واحد افزایش بده تا به فضای خالی بعدی اشاره کند.
- عنصر دادهای را به موقعیت مورد نظر در پشته اضافه کن.
- گام 5: پیام موفقیت را برگردان.
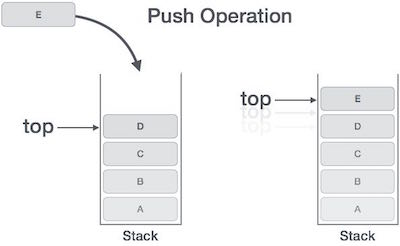
اگر از لیست پیوندی برای پیادهسازی پشته استفاده شود، در این صورت در گام 3 باید فضا به صورت دینامیک تخصیص یابد.
الگوریتم عملیات push
یک الگوریتم ساده برای عملیات push را میتوان به صورت زیر نوشت:
begin procedure push: stack, data
if stack is full
return null
endif
top ← top + 1
stack[top] ← data
end procedure
پیادهسازی الگوریتم در زبان C بسیار ساده است کد زیر را ببینید.
void push(int data) {
if(!isFull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}
عملیات POP
دسترسی به محتوای پشته در هنگام حذف آن، به نام عملیات pop شناخته میشود. در پیادهسازی آرایهای از عملیات ()pop، عنصر دادهای واقعاً حذف نمیشود، بلکه به جای آن مقدار top یک واحد کاهش مییابد تا به مقدار کمتری در پشته اشاره کند. اما در پیادهسازی لیست پیوندی عملیات ()pop واقعاً عنصر دادهای را از فضای تخصیص یافته پشته پاک میکند. یک عملیات pop میتواند شامل گامهای زیر باشد:
- گام 1: بررسی کن که پشته خالی است یا نه؟
- گام 2: اگر پشته خالی بود، یک خطا اعلام کن و خارج شو.
- گام 3: اگر پشته خالی نبود، عنصر دادهای را که top مورد اشاره قرار میدهد برگردان.
- گام 4: مقدار top را یک واحد کم کن.
- گام 5: پیام موفقیت را بازگردان.

الگوریتم عملیات pop
یک الگوریتم ساده برای عملیات pop میتواند به شکل زیر باشد:
begin procedure pop: stack
if stack is empty
return null
endif
data ← stack[top]
top ← top - 1
return data
end procedure
پیادهسازی الگوریتم فوق در زبان C چنین است:
int pop(int data) {
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
} else {
printf("Could not retrieve data, Stack is empty.\n");
}
}
در ادامه پیادهسازی کامل ساختمان داده پشته را در زبان C مشاهده میکنید:
#include
int MAXSIZE = 8;
int stack[8];
int top = -1;
int isempty() {
if(top == -1)
return 1;
else
return 0;
}
int isfull() {
if(top == MAXSIZE)
return 1;
else
return 0;
}
int peek() {
return stack[top];
}
int pop() {
int data;
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
} else {
printf("Could not retrieve data, Stack is empty.\n");
}
}
int push(int data) {
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}
int main() {
// push items on to the stack
push(3);
push(5);
push(9);
push(1);
push(12);
push(15);
printf("Element at top of the stack: %d\n" ,peek());
printf("Elements: \n");
// print stack data
while(!isempty()) {
int data = pop();
printf("%d\n",data);
}
printf("Stack full: %s\n" , isfull()?"true":"false");
printf("Stack empty: %s\n" , isempty()?"true":"false");
return 0;
}
اگر کد فوق را کامپایل و اجرا کنید، نتیجه زیر به دست میآید:
خروجی
Element at top of the stack: 15 Elements: 15 12 1 9 5 3 Stack full: false Stack empty: true

تجزیه عبارتهای حسابی
روش نگارش عبارتهای حسابی به نام نمادگذاری (notation) نامیده میشود. عبارتهای حسابی را میتوان به سه روش نمادگذاری مختلف؛ اما معادل هم نوشت، یعنی بدون تغییر دادن مفهوم یا خروجی عبارت. این نمادگذاریها به صورت زیر هستند:
- نمادگذاری میانوندی (Infix)
- نمادگذاری پیشوندی (Prefix)
- نمادگذاری پسوندی (Postfix)
این نمادگذاریها به روش استفاده از عملگرها در عبارت مربوط میشوند. در این بخش از نوشته به مرور این نمادگذاریها خواهیم پرداخت.
نمادگذاری میانوندی
ما زمانی از نمادگذاری میانوندی برای نوشتن عبارتهای حسابی خود استفاده میکنیم که عملگرهای مورد استفاده میان عملوندها قرار گرفته باشند، برای مثال a + b + c. نوشتن و خواندن عبارتهای حسابی به روش میانوندی برای ما به عنوان انسان آسانتر است؛ اما در مورد ماشینهای محاسباتی این وضع کمی فرق میکند. یک الگوریتم برای پردازش نمادگذاری میانوندی، بر حسب زمان و فضای مورد نیاز برای محاسبات دشوار و پرهزینه است.
نمادگذاری پیشوندی
این نوع از نمادگذاری به نام نمادگذاری لهستانی معکوس نیز شناخته میشود. در این سبک از نمادگذاری، عملگر به عنوان پسوندی برای عملوندها در نظر گرفته میشود، یعنی عملگر پس از عملوند نوشته میشود. برای مثال ab+ که معادل روش نمادگذاری میانوندی a + b است و به نام نمادگذاری لهستانی نیز شناخته میشود.
نمادگذاری پسوندی
این سبک از نمادگذاری به نام لهستانی معکوس نامیده میشود. در این روش، عملگر به صورت پسوند عملوندها نوشته میشود، یعنی عملگر پس از عملوند قرار میگیرد. برای مثال +ab معادل نماد گذاری میانوندی a + b است.
در جدول زیر به طور خلاصه تفاوت بین هر سه روش نمادگذاری را میتوانید مشاهده کنید:
| ردیف | نمادگذاری میانوندی | نماد گذاری پیشوندی | نماد گذاری پسوندی |
|---|---|---|---|
| 1 | a + b | + a b | a b + |
| 2 | (a + b) ∗ c | ∗ + a b c | a b + c ∗ |
| 3 | a ∗ (b + c) | ∗ a + b c | a b c + ∗ |
| 4 | a / b + c / d | + / a b / c d | a b / c d / + |
| 5 | (a + b) ∗ (c + d) | ∗ + a b + c d | a b + c d + ∗ |
| 6 | ((a + b) ∗ c) - d | - ∗ + a b c d | a b + c ∗ d - |
تجزیه عبارتها
همان طور که قبلاً اشاره کردیم استفاده از نمادگذاری میانوندی برای تجزیه عبارتهای حسابی در یک برنامه یا الگوریتم کار چندان بهینهای محسوب نمیشود؛ بلکه بهتر است ابتدا این نمادگذاریهای میانوندی به یکی از نمادگذاریهای پیشوندی یا پسوندی تبدیل شوند و سپس محاسبات انجام شود. برای تجزیه هر عبارت حسابی باید تقدم و وابستگی عملگرهای مربوطه را در نظر بگیریم.
تقدم
زمانی که یک عملوند بین دو عملگر مختلف قرار میگیرد، کدام عملگر باید ابتدا روی عملوند اعمال شود؟ این مسئله از طریق تعیین تقدم یک عملگر نسبت به عملگرهای دیگر مشخص میشود. برای مثال:

از آنجا که عملیات ضرب نسبت به جمع تقدم دارد، b * c ابتدا محاسبه میشود. جدولی از تقدم عملگرهای مختلف در ادامه ارائه شده است.
وابستگی
وابستگی، قاعده نحوه نمایش عملگرهای با تقدم یکسان را تعیین میکند. برای نمونه در عبارت a + b – c هر دو عملگر + و – تقدم یکسانی دارند، در این صورت این که کدام بخش از عبارت باید ابتدا محاسبه شود از سوی وابستگی این عملگرها مشخص میشود. در این مثال هر دو عملگر + و – وابستگی چپ دارند و از این رو عبارت به صورت زیر ارزیابی میشود:
(a + b) − c
تقدم و وابستگی ترتیب ارزیابی یک عبارت را مشخص میسازند. در ادامه جدولی ارائه شده است که در آن تقدم و وابستگی عملگرهای مختلف را با ترتیب نزولی میتوانید مشاهده کنید.
| ردیف | عملگر | تقدم | وابستگی |
|---|---|---|---|
| 1 | توان ^ | بالاترین | وابستگی راست |
| 2 | ضرب ( ∗ ) و تقسیم ( / ) | رده دوم | وابستگی چپ |
| 3 | جمع( + ) و تفریق ( − ) | پایین ترین | وابستگی چپ |
جدول فوق تقدم پیشفرض عملگرها را نشان میدهد. در هر زمان میتوان ترتیب عملگرهای یک عبارت حسابی را با استفاده از پرانتز تغییر داد. برای نمونه در عبارت a + b * c بخش b * c ابتدا ارزیابی میشود، چون ضرب نسبت به جمع نقدم دارد. اما اگر به صورتزیر از پرانتز استفاده کنیم، میتوانیم کاری کنیم که a + b ابتدا ارزیابی شود:
(a + b) * c

الگوریتم ارزیابی پسوندی
اینک میتوانیم الگوریتم روش ارزیابی نمادگذاری پسوندی را بررسی کنیم:
- گام 1: عبارت را از سمت چپ شروع به اسکن کن.
- گام 2: اگر عملوندی وجود داشت، آن را به پشته بفرست.
- گام 3: اگر یک عملگر وجود داشت، عملوند را از پشته فراخوانی کرده و عملیات را اجرا کن.
- گام 4: خروجی گام 3 را دوباره در پشته ذخیره کن.
- گام 5: عبارت را تا زمانی که همه عملوندها مصرف ودند ادامه بده.
- گام 6: عملیات pop را روی پشته انجام بده و عملیات را تکمیل کن.
پیادهسازی در زبان C
همانم طور که قبلاً اشاره کردیم، گرچه نمادگذاری میانوندی برای مطالعه و درک انسان راحتتر است؛ ولی دستگاههای الکترونیکی مانند رایانهها، روش نمادگذاری پسوندی را برای تجزیه عبارتهای حسابی ترجیح میدهند. در ادامه برنامهای برای تبدیل نمادگذاری میانوندی به نمادگذاری پسوندی میبینید:
#include
#include
//char stack
char stack[25];
int top = -1;
void push(char item) {
stack[++top] = item;
}
char pop() {
return stack[top--];
}
//returns precedence of operators
int precedence(char symbol) {
switch(symbol) {
case '+':
case '-':
return 2;
break;
case '*':
case '/':
return 3;
break;
case '^':
return 4;
break;
case '(':
case ')':
case '#':
return 1;
break;
}
}
//check whether the symbol is operator?
int isOperator(char symbol) {
switch(symbol) {
case '+':
case '-':
case '*':
case '/':
case '^':
case '(':
case ')':
return 1;
break;
default:
return 0;
}
}
//converts infix expression to postfix
void convert(char infix[],char postfix[]) {
int i,symbol,j = 0;
stack[++top] = '#';
for(i = 0;i<strlen(infix);i++) { symbol = infix[i]; if(isOperator(symbol) == 0) { postfix[j] = symbol; j++; } else { if(symbol == '(') { push(symbol); } else { if(symbol == ')') { while(stack[top] != '(') { postfix[j] = pop(); j++; } pop(); //pop out (. } else { if(precedence(symbol)>precedence(stack[top])) {
push(symbol);
} else {
while(precedence(symbol)<=precedence(stack[top])) {
postfix[j] = pop();
j++;
}
push(symbol);
}
}
}
}
}
while(stack[top] != '#') {
postfix[j] = pop();
j++;
}
postfix[j]='\0'; //null terminate string.
}
//int stack
int stack_int[25];
int top_int = -1;
void push_int(int item) {
stack_int[++top_int] = item;
}
char pop_int() {
return stack_int[top_int--];
}
//evaluates postfix expression
int evaluate(char *postfix){
char ch;
int i = 0,operand1,operand2;
while( (ch = postfix[i++]) != '\0') {
if(isdigit(ch)) {
push_int(ch-'0'); // Push the operand
} else {
//Operator,pop two operands
operand2 = pop_int();
operand1 = pop_int();
switch(ch) {
case '+':
push_int(operand1+operand2);
break;
case '-':
push_int(operand1-operand2);
break;
case '*':
push_int(operand1*operand2);
break;
case '/':
push_int(operand1/operand2);
break;
}
}
}
return stack_int[top_int];
}
void main() {
char infix[25] = "1*(2+3)",postfix[25];
convert(infix,postfix);
printf("Infix expression is: %s\n" , infix);
printf("Postfix expression is: %s\n" , postfix);
printf("Evaluated expression is: %d\n" , evaluate(postfix));
}
اگر کد فوق را کامپایل و اجرا کنیم، نتیجه زیر به دست میآید:
خروجی
Infix expression is: 1*(2+3) Postfix expression is: 123+* Result is: 5
صف
صف یک ساختار داده است که تا حدودی شبیه پشته محسوب میشود؛ اما بر خلاف پشته، صف از هر دو سمت باز است. از یک سمت همواره برای درج دادهها و از سمت دیگر برای حذف دادهها استفاده میشود. صف از روش FIFO (ورودی اول-خروجی اول) استفاده میکند. در این روش هر دادههای که اول در صف ذخیره شود، هنگام خروج نیز قبل از همه خارج میشود.

نمونهای از صف در دنیای واقعی میتواند یک خیابان یکطرفه باشد که در آن وسایل نقلیهای که اول وارد خیابان شده باشند، قبل از بقیه از آن خارج میشوند. مثالها زیادی از صف در دنیای واقعی میتوان مشاهده کرد، از صفهای خرید بلیت تا ایستگاههای اتوبوس.
نمایش صف
اینک که با مفهوم صف آشنا شدیم، میدانیم که میتوانیم از هر دو انتها به صف دسترسی داشته باشیم و برای این مسئله دلایل مختلفی وجود دارد. در نمودار زیر سعی کردهایم نمایش صف به عنوان یک ساختار داده را به زبانی گویا نشان دهیم:

صف را نیز مانند پشته میتوان با استفاده از آرایهها، لیستهای پیوندی، اشارهگرها و ساختارها پیادهسازی کرد. به دلیل سادگی در این راهنما صف را با استفاده از آرایه یک بعدی پیادهسازی میکنیم.
عملیاتهای ابتدایی
عملیاتهای صف میتواند شامل راهاندازی یا تعریف، استفاده و سپس حذف کامل آن از حافظه باشد. در ادامه تلاش خواهیم کرد تا عملیاتهای ابتدایی مرتبط با صفها را بررسی کنیم:
- ()enqueue: یک آیتم را به صف اضافه (ذخیره) میکند.
- ()dequeue: یک آیتم را از صف حذف میکند (مورد دسترسی قرار میدهد).
چند کارکرد دیگر نیز هستند که برای کارآمدسازی عملیاتهای فوق در صف ضروری هستند:
- ()peek: یک عنصر را بدون حذف کردن، از ابتدای صف دریافت میکند.
- ()isfull: پر بودن صف را بررسی میکند.
- ()isempty: خالی بدون صف را بررسی میکند.
ما در صف همواره با استفاده از اشارهگر front دادهها را حذف میکنیم (مورد دسترسی قرار میدهیم) و با استفاده از اشارهگر rear آنها را اضافه میکنیم. ابتدا کارکردهای پشتیبانی یک صف را بررسی میکنیم:
()Peek
این تابع به دیدن دادههای در ابتدا (front) صف کمک میکند. الگوریتم ()peek به صورت زیر است:
begin procedure peek return queue[front] end procedure
پیادهسازی تابع ()peek در زبان C به صورت زیر است:
int peek() {
return queue[front];
}
()isfull
از آنجا که ما برای پیادهسازی صف از آرایه تک بُعدی استفاده کردهایم، کافی است اشارهگر rear را برسی کنیم تا به MAXSIZE صف دسترسی پیدا کنیم و تعیین کنیم که صف پر شده است یا نه. در حالتی که صف با استفاده از یک لیست پیوندی پیادهسازی میشود، الگوریتم کمی متفاوت خواهد بود. الگوریتم تابع ()isfull به صورت زیر است:
begin procedure isfull
if rear equals to MAXSIZE
return true
else
return false
endif
end procedure
پیادهسازی تابع ()isfull در زبان C نیز به صورت زیر است:
bool isfull() {
if(rear == MAXSIZE - 1)
return true;
else
return false;
}
()isempty
الگوریتم این تابع به صورت زیر است:
begin procedure isempty
if front is less than MIN OR front is greater than rear
return true
else
return false
endif
end procedure
اگر مقدار front کمتر از MIN یا صفر باشد، در این صورت مشخص میشود که صف هنوز مقداردهی اولیه نشده است و از این رو خالی است. در ادامه کد تابع ()isempty در زبان C ارائه شده است:
bool isempty() {
if(front < 0 || front > rear)
return true;
else
return false;
}
عملیات Enqueue
صفها دو اشارهگر داده را نگهداری میکنند که front و rear نام دارند. از این رو پیادهسازی عملیاتهای آنها نسبت به پشتهها کاملاً پیچیدهتر است. در ادامه گامهایی که برای ذخیرهسازی یا درج یک داده در صف مورد نیاز است را میبینید:
- گام 1: بررسی کن که آیا صف پر است یا نه.
- گام 2: اگر صف پر بود، خطای overflow را صادر کرده و خارج شو.
- گام 3: اگر صف پر نبود، مقدار اشارهگر rear را یک واحد افزایش بده تا به فضای خالی بعدی اشاره کند.
- گام 4: عنصر دادهای را به موقعیت صف که اشارهگر rear نشان میدهد، اضافه کن.
- گام 5: پیام موفقیت را بازگردان.

برخی اوقات باید بررسی کنیم که آیا صف مقداردهی اولیه شده یا نه تا بتوانیم موقعیتهای پیشبینینشده را نیز مدیریت کنیم.
الگوریتم عملیات enqueue در صف
procedure enqueue(data)
if queue is full
return overflow
endif
rear ← rear + 1
queue[rear] ← data
return true
end procedure
پیادهسازی تابع enqueuer() در زبان C
int enqueue(int data)
if(isfull())
return 0;
rear = rear + 1;
queue[rear] = data;
return 1;
end procedure
عملیات dequeue
دسترسی به دادههای یک صف، فرایندی دومرحلهای است: دسترسی به دادهای که اشارهگر front نشان میدهد و حذف داده پس از دسترسی. گامهای زیر برای اجرای عملیات dequeue مورد نیاز هستند:
- گام 1: بررسی کن که صف خالی است یا نه.
- گام 2: اگر صف خالی بود خطای overflow را صادر کرده و خارج شو.
- گام 3: اگر صف خالی نبود، به دادهای که اشارهگر front نشان میدهد، دسترسی ایجاد کن.
- گام 4: اشارهگر front را یک واحد افزایش بده تا به موقعیت بعدی اشاره کند.
- گام 5: پیام موفقیت را بازگردان.
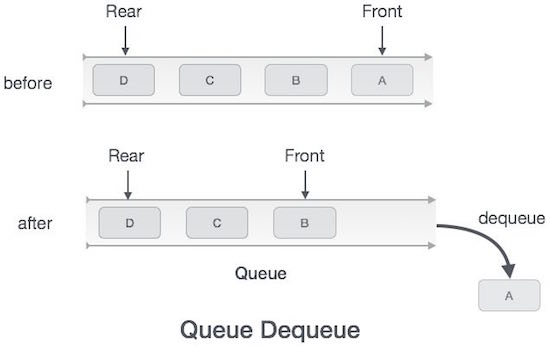
الگوریتم عملیات dequeue
procedure dequeue
if queue is empty
return underflow
end if
data = queue[front]
front ← front + 1
return true
end procedure
پیادهسازی تابع dequeue در زبان C:
int dequeue() {
if(isempty())
return 0;
int data = queue[front];
front = front + 1;
return data;
}
در ادامه کد کامل پیادهسازی ساختار صف در زبان C را مشاهده میکنید:
#include
#include
#include
#include
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek() {
return intArray[front];
}
bool isEmpty() {
return itemCount == 0;
}
bool isFull() {
return itemCount == MAX;
}
int size() {
return itemCount;
}
void insert(int data) {
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int removeData() {
int data = intArray[front++];
if(front == MAX) {
front = 0;
}
itemCount--;
return data;
}
int main() {
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
// front : 0
// rear : 4
// ------------------
// index : 0 1 2 3 4
// ------------------
// queue : 3 5 9 1 12
insert(15);
// front : 0
// rear : 5
// ---------------------
// index : 0 1 2 3 4 5
// ---------------------
// queue : 3 5 9 1 12 15
if(isFull()) {
printf("Queue is full!\n");
}
// remove one item
int num = removeData();
printf("Element removed: %d\n",num);
// front : 1
// rear : 5
// -------------------
// index : 1 2 3 4 5
// -------------------
// queue : 5 9 1 12 15
// insert more items
insert(16);
// front : 1
// rear : -1
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
// As queue is full, elements will not be inserted.
insert(17);
insert(18);
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
printf("Element at front: %d\n",peek());
printf("----------------------\n");
printf("index : 5 4 3 2 1 0\n");
printf("----------------------\n");
printf("Queue: ");
while(!isEmpty()) {
int n = removeData();
printf("%d ",n);
}
}
اگر کد فوق را کامپایل و اجرا کنیم، نتیجه زیر به دست میآید:
خروجی
Queue is full! Element removed: 3 Element at front: 5 ---------------------- index : 5 4 3 2 1 0 ---------------------- Queue: 5 9 1 12 15 16
امیدواریم از مطالعه این نوشته لذت برده و با ساختارهای مهم دادهای که در این راهنما معرفی کردیم، به طور کامل آشنا شده باشید. اجرای عملی کدها و پیادهسازی آنها که در این راهنما معرفی شده است، موجب میشوند که درک بهتری از این ساختارهای دادهای کسب کنید.













سلام.ممنونم عالی بود توضیحاتتون
تابعي بنويسيد كه رشته اي را دريافت كند و با استفاده از پشته و صف بررسي كند كه آيا رشته متقارن هست يا خير؟
مثال:
ABCDCBA
ABCCBA
يعني از هر طرف بخوانيم يكي باشد.
لطفا راهنمایی کنید.
چطور میتونم کلیدهای میانبری رو در صف تعریف کنم اگر شرط برقرار بود مثلا فرم خاصی و نشان بده مثلا من میخوام کلیدهای 2a , 3b,25,56, در صف قرار بدم اگر کسی 2a رو در کیبورد فشار داد فرم ۱ با بشه به همین ترتیب اگر کسی در فرم اصلی ۳b را فشار داد فرم ۲ باز بشه در زبان vb یا c# ممنون از راهنماییتون
عالی
سلام ممنون بابت مطالب مفیدتون . سورسی که برای پشته گزاشتین که به زبان سی هستش اجرا نمیشه کامپایلرم کردم. من سورس ایجاد استک و درج و حذف و نمایش عناصر رو میخواستم میشه لطف کنید قرار بدینش ممنون میشم
سلام خسته نباشین
من یک مسئله بهینه سازی با استفاده از الگوریتم queuing search دارم در نرم افزار متلب میشه کمکم کنید کدش رو از کجا پیدا کنم
با سلام من از شما تشکر می کنم یک نیاز فوری دارم من باید خیلی فوری آموزش کامل سی شارپ در کنسول را تهیه کنم خواهشمندم اگر سری کاملی دارید که در کنسول هست به من معرفی کنید باید سریع خریداری نمایم.
با تشکر از شما.
منظورم صف (Queue) بود نه Stack
#داداش من تو این کد فقط از تک کوتیشن استفادا کردم#
#و اینکه فکر نکن حلقه بی نهایت هست چون تعداد دور#
#حلقه نا مشخص هست کد رو اینجوری نوشتم#
#بهش اعتماد نداری اول تو کامپایلر آنلاین تستش کن#
# این کد بدون پشته هست ولی کوتاه هست و کارت رو راه#
#میندازه😀#
(”)my_string=input
”=Xstring
y=-1
:try
: while 1
Xstring=Xstring+my_string[y]
y=y-1
:except
:if Xstring==my_string
(‘رشته متقارن است’)print
:else
(‘رشته نا متقارن است’)print
سلام
در بخش دوم همان نوشته به صف هم اشاره شده است.
با تشکر
با سلام و خسته نباشید
اگه مشیه هیمن کد رو با زبان سی شارپ و توی فرم اپلیکیشن بنویسید
به خدا خیلی لازم دارم اگه اینو تا شنبه هفته بعدی نبرم به استاد درس ساختمان داده رو افتادم
سلام دوست عزیز؛
من دقیقاً متوجه نشدم، منظورتان از فرم اپلیکیشن چیست، اما معادل #C کدی که در این مقاله نوشته شده را میتوانید در این لینک (+) ملاحظه کنید.
موفق باشید.