الگوریتم اقلیدسی – به زبان ساده

در این مطلب، «الگوریتم اقلیدسی» (Euclidean Algorithm) برای محاسبه بزرگ‌ترین مقسوم‌علیه مشترک (ب.م.م) مورد بررسی قرار گرفته است. «علوم کامپیوتر» (Computer Science)، علمی پیرامون کامپیوترها است (دستکم بر اساس تعریف). مفهوم کامپیوترها برای اولین بار در سال ۱۸۰۰ بیان شد. کامپیوترها منجر به انقلابی در جوامع انسانی و صنایع شدند و می‌توان به جرات گفت که امروزه دیگر انسان‌ها نمی‌توانند به زندگی بدون وجود این کامپیوترها فکر کنند. این در حالی است که الگوریتم‌ها قدمت بیشتری دارند و هزاران سال است که وجود داشته‌اند. برخی از الگوریتم‌های اولیه‌ای که در دوران‌های بسیار دور معرفی شده‌اند، به طرز عجیبی همچنان کاربرد دارد.

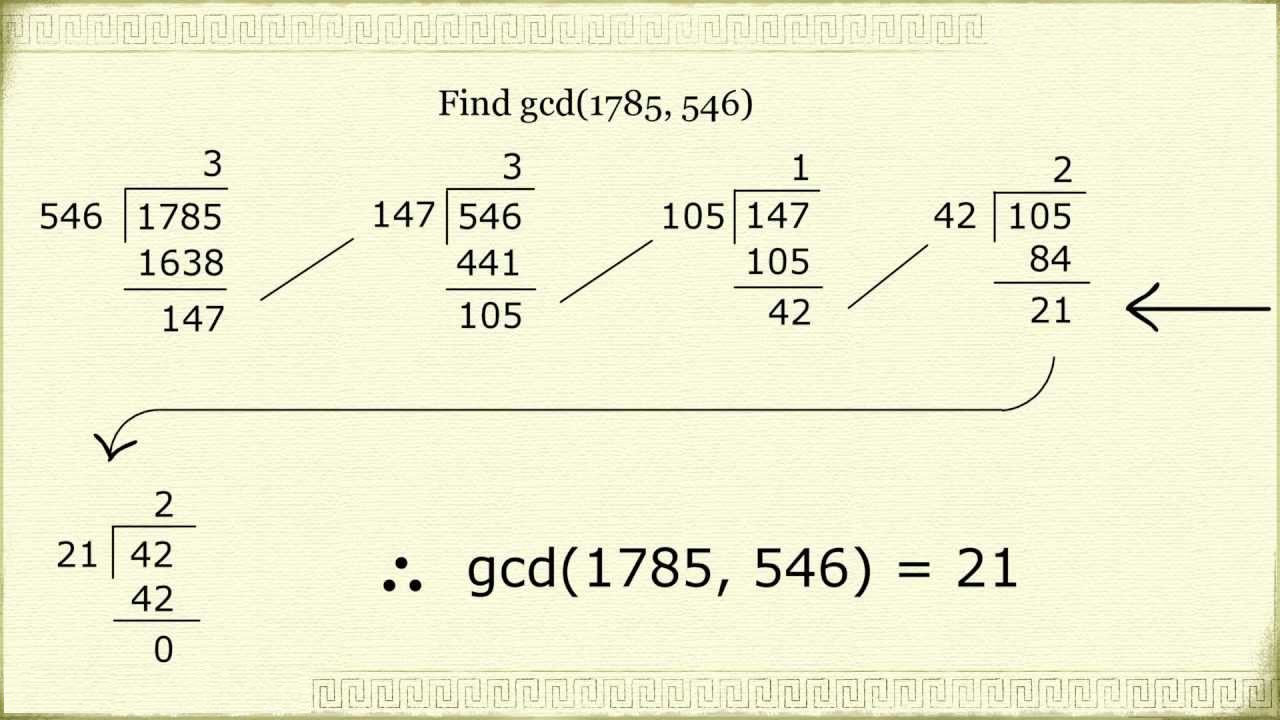
یکی از این الگوریتم‌ها به نام «الگوریتم اقلیدسی» (Euclidean Algorithm) در کتاب «اصول اقلیدس» (Euclid's Elements) آمده و مربوط به ۳۰۰ سال پیش از میلاد مسیح است. این الگوریتم، یک راهکار ساده برای پیدا کردن «بزرگ‌ترین مقسوم‌علیه مشترک» یا «ب.م.م» (Greatest Common Divisor | GCD) دو عدد است و در موارد گوناگونی مانند کاهش کسرها کاربرد دارد. اولین روشی که توسط اقلیدس معرفی شده است، از تفریق ساده استفاده می‌کند.

function euclid_sub(a::Int64, b::Int64)
    a = abs(a)
    b = abs(b)

    while (a != b)
        if (a > b)
            a -= b
        else
            b -= a
        end
    end

    return a
end

در اینجا، هر دو عدد به صورت یک خط رو به بالا کشیده می‌شوند و در هر گام، عدد کوچکتر از عدد بزرگ‌تر تفریق می‌شود. هنگامی که هر دو مقدار با یکدیگر برابر شدند، به مقدار حاصل، «بزرگ‌ترین مقسوم‌علیه مشترک» گفته می‌شود.

نمودار دو عدد a و b و تغییرات آن‌ها در گام‌های مختلف، به صورت زیر است.

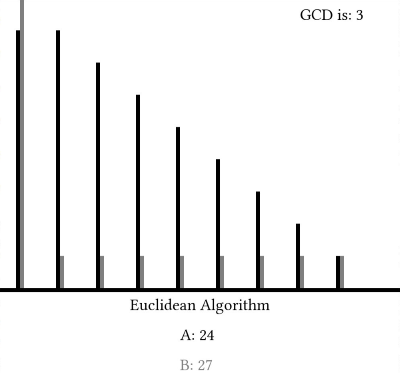
پیاده‌سازی نوین این الگوریتم، معمولا با استفاده از عملگر باقیمانده انجام می‌شود و به صورت زیر است.

function euclid_mod(a::Int64, b::Int64)
    a = abs(a)
    b = abs(b)

    while(b != 0)
        b,a = a%b,b
    end

    return a
end

در اینجا، b به عنوان باقی‌مانده a%b و a برابر با مقداری است که b در گام پیشین بوده است. با توجه به چگونگی کار کردن عملگر ماژول‌ها، خروجی این روش نیز مشابه با روش مبتنی بر تفریق است. اما با نشان دادن تغییرات a و b در هر گام، می‌توان نشان داد که این روش نسبت به روش پیشین، نیاز به گام‌های کمتری دارد.

فیلم مجموعه آموزش ساختمان داده و طراحی الگوریتم – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

روش اقلیدسی، مبنایی برای بسیاری از الگوریتم‌های دیگر در تاریخ علوم کامپیوتر است و در الگوریتم‌های آینده نیز استفاده خواهد شد. این نکته نیز جالب توجه است که یک الگوریتم بسیار قدیمی، همچنان دارای کاربردهای نوین است. البته، الگوریتم‌های متعدد دیگری نیز وجود دارند که می‌توان از آن‌ها برای محاسبه بزرگ‌ترین مقسوم‌علیه مشترک دو عدد استفاده کرد و نسبت به روش اقلیدسی نیز در برخی موارد، بهتر عمل می‌کنند. اینکه امروز و پس از گذشت بالغ بر دو هزار سال از مرگ اقلیدس، پیرامون روش‌های ارائه شده توسط او صحبت می‌شود، نشانگر محدود نبودن ریاضیات به زمان و جغرافیا است.

• مجموعه آموزش‌های دروس ریاضیات
• مجموعه آموزش‌های دروس علوم و مهندسی کامپیوتر
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• ب م م یا بزرگترین مقسوم علیه مشترک چیست؟ — به زبان ساده
• ک م م یا کوچکترین مضرب مشترک چیست؟ — به زبان ساده

^^