نظریه میدان های کوانتومی چیست؟ – به زبان ساده
انسان از ۲۵۰۰ سال قبل تاکنون به دنبال آن بوده که کیهان از چه چیزی ساخته شده است. چند سال قبل، فیلسوفی به نام دموکریت ادعا کرد که کیهان و تمام اجزای آن از ذراتی به نام اتم تشکیل شدهاند. این فیلسوف، اتمها را کوچکترین اجزای سازنده ماده دانست. اما با پیشرفت علم مشخص شد که اتمها از ذرات کوچکتری به نام الکترون، پروتون و نوترون ساخته شدهاند. سالها بعد مشخص شد که ذرات بنیادی دیگری مانند کوارکها و گلوئونها، سازنده پروتون یا نوترون هستند. این تمام ماجرا نبود. در سال ۲۰۱۲، ذره بنیادی دیگری به نام بوزون هیگز کشف شد. اما نکته مهم در مورد این ذره، میدان مربوط به آن به نام میدان هیگز بود. اینجا بود که انقلاب بزرگی در نظریه میدان های کوانتومی رخ داد. در این مطلب، در مورد این نظریه و دستاوردهای آن صحبت خواهیم کرد.


نظریه میدان های کوانتومی چیست ؟
جدول تناوبی عناصر را در نظر بگیرید. سالها قبل دانشمندان به این نتیجه رسیدند که هر مادهای در جهان، حداقل از یکی از عناصر جدول تناوبی ساخته شده است. این موفقیت بزرگی در علم شیمی بود، اما از دیدگاه فیزیک، چیزی فراتر از عناصر جدول تناوبی وجود داشت.
نخستین کسی که عناصر جدول تناوبی را سازنده تمام اجزای کیهان ندانست، فیزیکدانی از دانشگاه کمبریج به نام «جی جی تامسون» (J. J. Thomson) بود. او در سال ۱۸۹۷ ذرهای کوچکتر از اتم، به نام الکترون، را کشف کرد. در آن زمان، دانشمندان بسیاری شگفتزده شدند و حتی برخی از آنها این کشف بزرگ را باور نکردند. ۱۵ سال پس از اعلام کشف الکترون توسط تامسون، فیزیکدانی به نام رادرفورد، اجزای سازنده اتم را کشف کرد.
اکنون میدانیم که هر اتمِ عنصری از هسته تشکیل شده است و الکترونها به دور آن در حرکت هستند. همچنین، میدانیم هسته از ذرات کوچکتری به نام نوترون و پروتون تشکیل شده است. تا سال ۱۹۷۰، فیزیکدانها بر این عقیده بودند که نوترونها و پروتونها، کوچکترین اجزای سازنده مواد مختلف در کیهان هستند، اما اینگونه نبود. در دهه ۷۰ میلادی، دانشمندان به کشف جدید در مورد ساختار داخلی پروتونها و نوترونها رسیدند. داخل هر پروتون و نوترون، سه ذره کوچکتر به نام کوارک قرار دارند. کوارکها به دو دسته کلی، کوارک بالا و پایین تقسیم میشوند. شاید از خود بپرسید آیا جهت کوارک بالا به سمت بالا و جهت کوارک پایین به سمت پایین است. خیر، هیچ دلیل مشخصی برای این نامگذاری وجود نداشت.
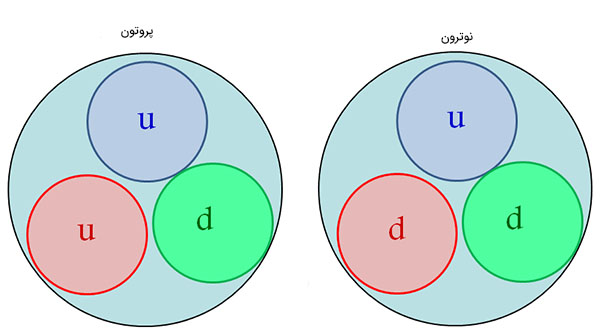
پروتون از دو کوارک بالا و یک کوارک پایین و در مقابل، نوترون از دو کوارک پایین و یک کوارک بالا، تشکیل شده است. بنابراین، میتوان نتیجه گرفت که ذرهای کوچکتر از الکترون و کوارکها وجود ندارند. از اینرو، سه ذره داریم که هر چیزی در جهان از آنها ساخته شده است. این نتیجه بسیار جالب است و به دانشآموزان در دبیرستان تدریس میشود. اما مشکلی در مورد این نتیجهگیری وجود دارد. در واقع، این نتیجهگیری دروغی بیش نیست. آنچه جهان را میسازد، الکترون و دو کوارک نیستند.
شاخهای از فیزیک وجود دارد که به ذرات بنیادی تکیه نکرده و بیانکننده یکی از بهترین نظریههای مطرح شده در مورد ساختار جهان هستی است. بر طبق این نظریه، اجزای بنیادی سازنده کیهان، ذرات نیستند. ساختار کیهان مفهومی بسیار انتزاعی دارد. سازنده کیهان همانند سیال، جریان دارد و در سراسر آن همانند امواج، پخش شده است و میدان نامیده میشود. برای درک بهتر این مفهوم، ابتدا آن را از دیدگاه یک فیزیکدان تعریف میکنیم. میدان در سراسر فضا پخش میشود و در هر نقطه از فضا، مقدار مشخصی دارد. این مقدار با گذشت زمان تغییر خواهد کرد.
کشف میدان
مفهوم میدان در حدود ۲۰۰ سال قبل، توسط فیزیکدانی به نام «مایکل فارادی» (Michael Faraday) مطرح شد. فارادی، دهها سال در مورد میدانهای الکتریکی و مغناطیسی و ويژگیهای آنها مطالعه کرد. او بینشی در مورد چگونگی عملکرد این میدانها، بنا کرد. امروزه به راحتی از میدانهای الکتریکی و مغناطیسی در زندگی روزمره استفاده میشود، اما باید بدانیم که فارادی یکی از انقلابیترین ایدهها را در فیزیک مطرح کرد.

دو آهنربا بردارید و آنها را از قطبهای شمال یا جنوب به یکدیگر نزدیک کنید. در ابتدا، چیزی احساس نمیشود، ولی هرچه فاصله دو آهنربا از یکدیگر کمتر شود، نیرویی در جهت مخالف حرکت آنها، احساس خواهد شد. در واقع، با نزدیک شدن دو آهنربا به یکدیگر، میدانی ساخته میشود و سعی در دور کردن آهنرباها از یکدیگر دارد. نبوغ فارادی در اینجا مشخص میشود. اینگونه به نظر میرسد که فضای بین دو آهن ربا خالی است، اما در واقع میدان مغناطیسی بین دو قطب مخالف شکل میگیرد و سعی در دور کردن آهنرباها از یکدیگر دارد. میدان مغناطیسی مفهومی فیزیکی و واقعی، اما نامریی است. فارادی نشان داد که با استفاده از میدان میتوان با افراد دیگر ارتباط برقرار کرد و بر اجسام دوردست تاثیر گذاشت. همچنین، فارادی پیشنهاد داد که نوسانات میدانهای الکتریکی و مغناطیسی، همان نور است. البته، پیشنهاد فارادی در حدود ۵۰ سال بعد توسط ماکسول اثبات شد. ۱۵۰ سال بعد، اهمیت کشف فارادی مشخص شد. در طول ۱۵۰ سال پس از کشف میدانهای الکتریکی و مغناطیسی توسط فارادی، انقلاب بزرگی در علم ایجاد شد.
تا سال ۱۹۲۰، ساختار جهان را مطابق ساختار تعیین شده توسط نیوتن و گالیله میدانستند. اما در دهه ۲۰ میلادی، فیزیکدانانی مانند هایزنبرگ و گالیله به این نتیجه رسیدند که جهان میکروسکوپی بسیار پیچیدهتر از آن است که تصور میشد. فیزیک کوانتوم در این دهه ۲۰ متولد شد و به دنبال آن نتایج شگفتآوری حاصل شد. یکی از نتیجههای عجیب بهدست آمده، گسسته بودن انرژی بود. به نقطه آغاز نظریه میدان های کوانتومی نزدیک میشویم. این نظریه از ترکیب دو مفهوم فیزیک کوانتوم و میدان، بهدست میآید:
- از یک سو ایده فارادی در مورد میدانهای الکتریکی و مغناطیسی را داریم. پدیدهای که در سراسر فضا پخش میشود و پیوسته است.
- از سوی دیگر، فیزیک کوانتوم و گسسته بودن انرژی را داریم.
سوالی که ممکن است مطرح شود آن است ترکیب این دو با یکدیگر، چه پیامد یا پیامدهایی دارد. نخستین پیامد آن است که چه اتفاقی برای میدانهای الکتریکی و مغناطیسی میافتد. همانطور که ابتدا فارادی و سپس ماکسول پیشنهاد دادند، امواج الکترومغناطیسی همان نور است. نور در فیزیک کلاسیک به طول کامل پیوسته است. حال فیزیک کوانتوم را برای نور استفاده میکنیم. در فیزیک کوانتوم، نور دیگر پیوسته نیست، بلکه از ذراتی به نام فوتون تشکیل شده است. اما این تمام ماجرا نیست. این اصل در مورد تمام ذرات موجود در جهان، صدق میکند.
هر جا باشید، چیزی به نام میدان الکترون در سراسر فضا پخش شده است. این میدان همانند سیالِ جاری در سراسر جهان پخش میشود. موجها و نوسانات این سیال الکترونی (میدان) با استفاده از قوانین فیزیک کوانتوم به یکدیگر گره میخورند و بسته انرژی را تشکیل میدهند. به این بستههای انرژی، الکترون میگوییم. اما این تمام ماجرا نیست. دو میدان مربوط به کوارک نیز وجود دارند. موجهای این میدانها، همان کوارک بالا و پایین هستند. این موضوع برای هر ذرهای در جهان برقرار است. میدانها زیربنای هر چیزی هستند. هر چیزی که به نام ذره بنیادی میشناسیم، در واقع امواج میدان یا بسته انرژی ایجاد شده در آن است. بنابراین، هیچ ذرهای در جهان وجود ندارد و میدانها اجزای بنیادی تشکیلدهنده جهان هستی هستند. این چشمانداز ما را به کجا میبرد؟
نوسانات خلأ کوانتومی
جعبهای بردارید و هر چیزی، مانند ذره و اتم، را از آن خارج کنید. آنچه در جعبه باقی می ماند، خلأ خالص است. فیزیکدانها با استفاده از مدل استاندارد ذرات، فضای تهی را شبیهسازی کردهاند. این شبیهسازی در تصویر زیر مشاهده میشود. همانطور که مشاهده میکنید، با وجود آنکه ذرات از جعبه خارج شدهاند، میدانها هنوز داخل آن وجود دارند. ذکر این نکته مهم است که قوانین حاکم بر میدانها، همان قوانین فیزیک کوانتوم است.
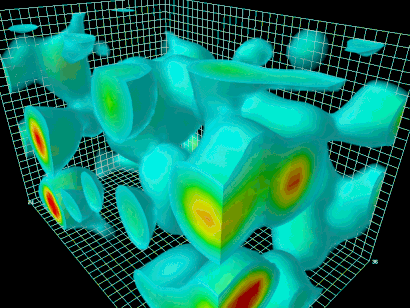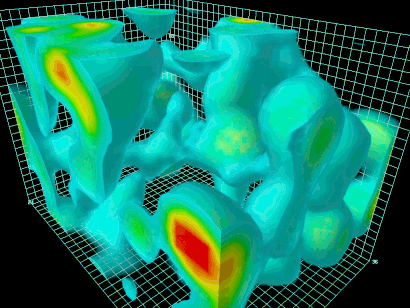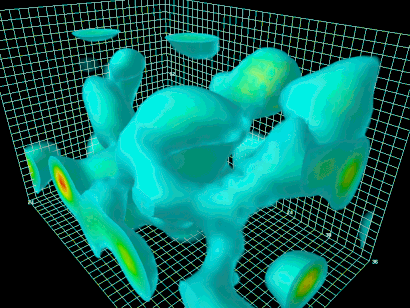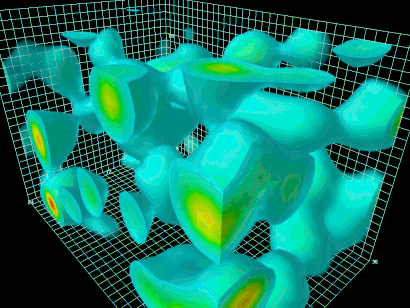
اصلی در فیزیک کوانتوم به نام اصل عدم قطعیت هایزنبرگ وجود دارد. بر طبق این اصل، هیچ چیز نمیتواند ساکن در جایی قرار بگیرد و میدانها باید از این اصل نیز پیروی کنند. به همین دلیل، با وجود آنکه هیچ چیز در جعبه وجود ندارد، میدانها باز هم نوسان میکنند. اما نوسان آنها بسیار پیچیدهتر از آن چیزی است که در ذهن میگنجد. به نوسان میدانها در فضای تهی، خلأ، «نوسانات خلأ کوانتومی» (Quantum Vacuum Fluctuations) گفته میشود. بنابراین، مفهوم هیچ در نظریه میدان های کوانتومی به صورت نوسان میدانها بیان میشود. نوسانات خلأ کوانتومی در حد نظریه باقی نماند، بلکه توسط آزمایشهای تجربی نیز تایید شده است.
شاید فکر کنید فضای تهی سادهترین چیزی است که میتوانید در جهان تصور کنید، اما حتی مفهوم هیچ یا خلأ نیز بسیار پیچیده است. اکنون، یک ذره یا جمعی از ذرات را تصور کنید. جریان بسیار پیچیدهتر خواهد شد. ریاضیات حاکم بر نظریه میدان های کوانتومی بسیار پیچیده است، به گونهای که معادلات گرانش اینشتین سادهتر به نظر میرسند. شش مساله در ریاضیات وجود دارند که هنوز توسط کسی حل نشده و یکی از آنها نظریه میدان های کوانتومی است.
قسمتهایی از نظریه میدان های کوانتومی به خوبی درک شدهاند. این حالت زمانی رخ میدهد که این میدانها بسیار آرام نوسان کنند. عدد به عنوان یکی از ویژگیهای مهم ذره الکترون در نظر گرفته میشود. الکترون ذرهای است که همانند زمین، به دور خود میچرخد. چرخش الکترون به دور خود را اسپین مینامیم. مدار اسپین، با استفاده از میدان مغناطیسی خارجی تغییر داده میشود. مدار اسپین الکترون در حضور میدان مغناطیسی خارجی، به آهستگی میچرخد. به این چرخش، تقدم میگوییم. سرعت تقدم محور اسپین در عدد نهفته است. این عدد را با دقت بالایی میتوان با استفاده از آزمایشهای تجربی اندازه گرفت. بنابراین، اندازهگیری به ما نشان میدهد که آیا قوانین حاکم بر جهان، به خصوص نظریه میدان های کوانتومی، را به خوبی فهمیدهایم یا خیر.
عدد از دو طریق محاسبه شده است:
- آزمایشهای بسیار دقیق فیزیکی در طول دهها سال انجام شدهاند.
- محاسبات دقیق که توسط فیزیکدانهای نظری انجام شده است.
به دو مقدار محاسبه شده برای در ادامه دقت کنید:
مقدارهای محاسبه شده تجربی و نظری برای ، در توافق کامل با یکدیگر هستند. این نزدیکی بین محاسبات نظری و آزمایشهای تجربی، در هیچ جایی از علم به اندازه مقدار محاسبه شده برای ، با یکدیگر در توافق کامل نبودند. چالش هنگامی آغاز میشود که نوسانات خلأ کوانتومی بسیار شدید میشوند. جرم پروتون را میتوان با انجام محاسبات ریاضی و حل چند معادله، بهدست آورد. جرم پروتون با دقتی برابر ۳ درصد محاسبه شده است. اما عدد بهدست آمده برای جرم پروتون باید بسیار دقیقتر باشد.
جدول تناوبی جدید
گرچه نظریه میدان های کوانتومی یکی از بهترین نظریه های مطرح شده در فیزیک است، اما درک ما از این نظریه نسبت به نظریههای دیگر فیزیک بسیار کمتر است. برای آنکه پیشرفت قابلقبولی در این زمینه داشته باشیم، باید به درک بهتری از نظریههای فیزیکی برسیم و این نظریهها را به کمک آزمایشهای تجربی تایید کنیم.
تاکنون با مفهوم کلی نظریه میدان های کوانتومی آشنا شدیم. در ادامه، میخواهیم بدانیم چه میدانهای کوانتومی در جهان وجود دارند. تعداد میدانهای کوانتومی در جهان زیاد نیست. جدول تناوبی در نظریه میدان های کوانتومی به شکل ساده زیر درآمده است:
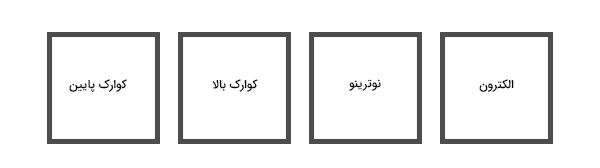
بار دیگر باید بر این موضوع تاکید کنیم که ذرات، اجزای سازنده کیهان نیستند، بلکه میدانهای زیربنای این ذرات، جهان را ساختهاند. علاوه بر الکترون و کوارکهای بالا و پایین، ذره چهارم دیگری به نام نوترینو نیز وجود دارد. نوترینوها همه جا هستند، اما متوجه آنها نمیشویم. ذکر این نکته مهم است که نوترینوها به راحتی با ماده برهمکنش نمیکنند. آیا این ذرات، تنها ذرات بنیادی در کیهان هستند؟ خیر، نکته عجیبی در اینجا وجود دارد که هیچ پاسخی برای آن نداریم. طبیعت، این چهار ذره را انتخاب و دو بار دیگر آنها را بازتولید کرده است. نام این ذرهها در تصویر زیر نشان داده شده است. در واقع، ۱۲ میدان داریم که این ذرات بنیادی را ساختهاند.
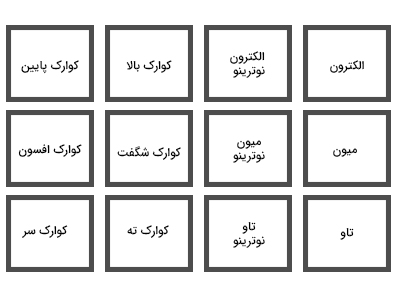
الکترون، نخستین ذره است. دو ذره دیگر وجود دارند که در هر زمینهای، همانند الکترون رفتار میکنند. تنها تفاوت این ذرهها با الکترون، جرم آنها است. این دو ذره میون و تاو نام دارند و جرم آنها به ترتیب، ۲۰۰ و ۳۰۰۰ برابر جرم الکترون است. تاکنون، هیچ دلیلی بر چرایی وجود این ذرات در طبیعت وجود ندارد. سه ذره دیگر، نوترینو هستند. علاوه بر دو کوارک بالا و پایین که در بالا گفته شد، چهار کوارک دیگر نیز به نام کوارکهای شگفت و افسون و سر و ته، وجود دارند. هر چیزی در کیهان، از این ۱۲ میدان ساخته شدهاند.
میدان های کوانتومی
این میدانها از طریق چهار نیروی بنیادی با یکدیگر برهمکنش میکنند:
- نیروی گرانش
- نیروی الکترومغناطیسی
- نیروی هستهای قوی
- نیروی هستهای ضعیف
با دو نیروی اول آشنا هستید. دو نیروی دیگر در مقیاس هسته اتم، وارد میشوند. نیروی هستهای قوی، کوارکها را داخل پروتون و نوترون، در کنار یکدیگر نگه میدارد. نیروی هستهای ضعیف نیز مسئول واپاشی پرتوزا در هستهها است. هر یک از این چهار نیرو با میدانها، مرتبط هستند. نیروی الکترومغناطیسی توسط فارادی کشف شد. میدانِ مرتبط با این نیرو، میدان گلوئون است. میدان مرتبط با نیروی گرانشی، میدان فضا-زمان است. بنابراین، جهانی که در آن زندگی میکنیم از ۱۲ میدان به نام میدان ماده به همراه ۴ میدان نیرو، ساخته شده است. ساختار جهان از ترکیب این ۱۶ میدان و برهمکنش آنها با یکدیگر، تشکیل میشود. برهمکنش این میدانها با یکدیگر بسیار جالب و پیچیده است.
کیهان سرشار از میدان است. فرض کنید یکی از ۱۲ میدان ماده، مانند میدان الکترون، شروع به نوسان میکند. این میدان به هنگام نوسان، به میدان دیگری مانند میدان الکترومغناطیسی ضربه وارد میکند. بنابراین، میدان الکترومغناطیسی نیز شروع به نوسان خواهد کرد. در ادامه، میدان الکترومغناطیسی در مسیر خود با میدان کوارک، برهمکنش میکند. میدان کوارک نیز شروع به نوسان خواهد کرد. در انتها، تمام میدانها به صورت هماهنگ و هارمونیک شروع به نوسان میکنند. نظریهای به نام مدل استاندارد، برای توضیح تمام این برهمکنشها و ساختار جهان توسط فیزیکدانها مطرح شده است. این نظریه به عنوان یکی از بزرگترین و بهترین نظریههای مطرح شده توسط فیزیکدانها، شناخته میشود.
تا اینجا در مورد همه میدانها، به جز یک میدان صحبت کردیم. این میدان، نخستین بار توسط فیزیکدانی اسکاتلندی به نام «پیتر هیگز» (Peter Higgs) پیشنهاد داده شد. در دهه ۷۰ میلادی، این میدان به میدانهای شناخته شده دیگر، اضافه شد. اما تا سال ۲۰۱۲، هیچ شاهد تجربی برای اثبات وجود این میدان، وجود نداشت. با کشف ذره بوزون هیگز در سال ۲۰۱۲، مدل استاندارد ذرات کامل شد. وجود ذره هیگز و میدان آن به دو دلیل بسیار اهمیت دارد:
- میدان هیگز مسئول جرم در کیهان است. جرم، مانند بار الکتریکی، یکی از بنیادیترین مشخصههای ماده است. مشخصههای بنیادی ماده یا ذره، مانند بار الکتریکی یا جرم، به چگونگی برهمکنش میدان آن با میدانهای دیگر مربوط میشود. به عنوان مثال، چگونگی برهمکنش میدان الکترون با میدان الکترومغناطیسی، بار الکتریکیِ الکترون را مشخص میکند. همچنین، جرم الکترون از برهمکنش میدان الکترون با میدان هیگز، تعیین میشود. بنابراین، برای درک جرم در طبیعت، باید با میدان هیگز آشنا باشیم.
- ذره هیگز یا میدان هیگز آخرین پازل مدل استاندارد برای تکمیل این نظریه بود. نکته جالب در مورد این ذره آن است که وجود آن ۵۰ سال قبل از کشف، پیشبینی شده بود.
معادله دیراک
گفتیم نظریه استاندارد ذرات یکی از بزرگترین نظریههای مطرح شده در فیزیک است و کشف ذره بوزون هیگز، پازل آن را کامل کرد. معادله پیچیده زیر، این مدل را به زبان ریاضی توصیف میکند:
گرچه هیچکس به طور کامل، تمام قسمتهای این معادله را درک نکرده است، اما نکته بسیار جالبی در مورد آن وجود دارد. این معادله، به درستی نتیجههای بهدست آمده از هر آزمایش تجربی در فیزیک را پیشبینی میکند. نتیجه هر آزمایشی در این معادله نهفته است. آشنایی با قسمتهای مختلف این معادله خالی از لطف نیست:
- : نخستین جمله مربوط به گرانش است و توسط اینشتین به معادله اضافه شد. اگر این قسمت از معادله را حل کنید، سرعت سقوط سیب از درخت یا هر چیز دیگری را به راحتی، پیشبینی خواهید کرد. حتی برخورد دو سیاهچاله با یکدیگر و تشکیل سیاهچاله جدید یا انبساط کیهان را به خوبی درک میکنید.
- : این قسمت از معادله توسط ماکسول نوشته شد و تمام اطلاعات لازم در میدان الکترومغناطیسی را به ما میدهد.
- : حل این قسمت از معادله، تمام اطلاعات لازم در مورد نیروی هستهای قوی را به ما میدهد.
- : حل این قسمت از معادله، تمام اطلاعات لازم در مورد نیروی هستهای ضعیف را به ما میدهد.
- : این قسمت از معادله توسط «پاول دیراک» (Paul Dirac)، فیزیکدان انگلیسی، نوشته شد و ماده یا ۱۲ ذره سازنده ماده را توصیف میکند.
- : این قسمت از معادله اصلی مربوط به معادلات بوزون هیگز است. با حل این قسمت، چگونگی برهمکنش ماده با میدان هیگز را درک خواهیم کرد.
بنابراین، تمام فیزیک در این معادله جمع شده است. این معادله، محدودیت کنونی علم فیزیک را مشخص میکند. تاکنون، هیچ آزمایشی انجام نشده است که توسط این معادله قابل توضیح نباشد. همچنین، فیزیکدانها هیچ راهی برای اثبات نادرستی این معادله نیافتهاند. بنابراین، این معادله بهترین معادله نوشته شده در علم فیزیک است. گرچه معادلهای بهتر از این معادله وجود ندارد، فیزیکدانها به دنبال چیزی بهتر از آن هستند. دلیل این موضوع آن است که در آیندهای نه چندان دور، آزمایشی انجام خواهد شد که توسط این معادله توصیف نمیشود.
ماده و انرژی تاریک
تاکنون، هر آزمایش تجربی توسط این معادله توصیف شده است، اما اسرار کیهان بسیار بیشتر از آزمایشهای انجام شده روی زمین است. ذرات نامریی زیادی در فضا وجود دارند، به گونهای که تعداد آنها از ذرات مریی بیشتر است. به این ذرات نامریی، ماده تاریک گفته میشود. اگر ماده تاریک دیده نمیشود، چگونه وجود آن اثبات میشود؟ ماده تاریک دیده نمیشود ولی بر محیط اطراف خود اثر میگذارد.
علاوه بر ماده تاریک، مفهوم عجیبتر دیگری نیز به نام انرژی تاریک در کیهان وجود دارد. انرژی تاریک در سراسر فضا پخش شده است. انرژی تاریک نیز نوعی میدان است که باعث میشود هر جسمی در کیهان، اجسام دیگر را دفع کند. در کسری از ثانیه پس از انفجار بزرگ، کیهان با سرعتی بسیار زیاد شروع به منبسط شدن کرد. سرعت انبساط کیهان در آن لحظه به قدری زیاد بود که فیزیکدانها نام آن را تورم گذاشتهاند. گرچه فیزیکدانها از وقوع تورم در نخستین لحظات پس از بیگبنگ اطمینان دارند، اما معادله حاکم بر مدل استاندارد نمیتواند آن را توضیح دهد. برای حرکت به جلو و کشف قوانین جدید حاکم بر جهان، باید به تمام پرسشهای بیپاسخ، پاسخ داده شود.
تشعشع پس زمینه کیهانی
کیهان در حدود ۱۳/۸ میلیارد سال قبل متولد شد. دانشمندان هیچ اطلاعی از چگونگی آغاز آن یا قبل از وقوع بیگبنگ ندارند، اما به خوبی میدانند پس از آن چه اتفاقی افتاد. تا ۳۸۰ هزار سال پس از وقوع بیگبنگ، کیهان از گلولههای آتش پر شده بود. وجود این گلولههای آتش در عکسی که از آن گرفته شده، به اثبات رسیده است. این تصویر، تشعشع پسزمینه کیهانی نام دارد و عکس آن را در ادامه مشاهده میکنید. دمای نقطههای قرمزرنگ بالاتر و دمای نقطههای آبیرنگ، کمتر است. به بیان دیگر، درخشش هر نقطه نسبت به نقطه دیگر در تصویر تغییر کرده است. این حالت شبیه سوسوی نور است. با مطالعه این تغییر درخشش یا سوسو کردن در تصویر، میتوان اطلاعاتی زیادی در مورد آغاز کیهان بهدست آورد.
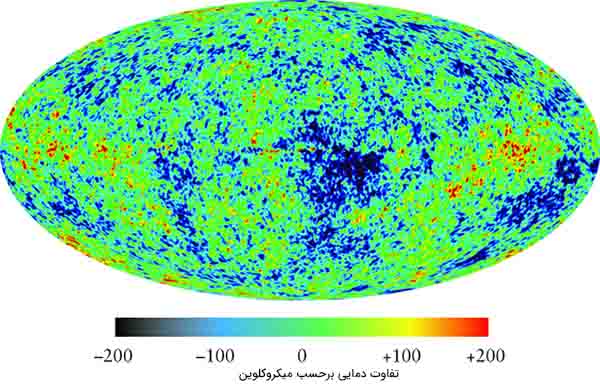
اما سوال اصلی آن است که چه چیزی تغییر درخشش در گلوله آتشین را به وجود آورد. پاسخ مشخصی برای این پرسش وجود دارد. گرچه عمر گلولههای آتشین پس از تولد کیهان در حدود ۳۸۰ هزار سال تخمین زده میشود، دلیل درخشش گلوله آتشین در این مدت زمان شکل نگرفته است. هر آنچه دلیل این درخشش بود، در نخستین لحظهها پس از تولد کیهان ایجاد شد. هنگامی که کیهان بسیار جوان بود، بلافاصله پس از بیگبنگ، هیچ ذرهای وجود نداشت. اما میدانهای کوانتومی وجود داشت، زیرا این میدانها در همه جا وجود دارند. نوسان این میدانهای کوانتومی در خلأ مطلق، در تصویر بالا نشان داده شده است.
در نخستین لحظهها پس از بیگبنگ، جهان به سرعت در حال منبسط شدن بود. این انبساط سریع منجر به گسترش نوسانات کوانتومی به سراسر کیهان و سپس انجماد آنها شد. بنابراین، نوسانات کوانتومی نشان داده شده در تصویر، همان نوسانها یا درخششهای مشاهده شده در گلوله آتشین آغاز جهان هستند. نوسانات کوانتومی تقریبا بلافاصله پس از بیگبنگ رخ دادند و پدیدهای کاملا میکروسکوپی هستند. اکنون این نوسانات در سراسر کیهان گسترش یافتهاند. پی بردن به وجود نوسانات کوانتومی، یکی از بزرگترین دستاوردهای نظریه میدان های کوانتومی است، اما سوالات زیادی نیز در این مورد به جا مانده است. به عنوان مثال، چه میدانی در تشعشع پسزمینه کیهانی نوسان میکند. برخی از فیزیکدانها حدس میزنند که میدان نوسانکننده، همان میدان هیگز است. اما برخی اعتقاد دارند میدان نوسانکننده، هیچکدام از میدانهای شناخته شده نیست.
در سالهای اخیر، تلاشهای زیادی برای کشف فیزیک فراتر از مدل استاندارد انجام شده است. به عنوان مثال، با استفاده از شتابدهندههایی مانند هادرون، سعی در کشف ذرات بنیادی جدید دارند. ذره بوزون هیگز در سال ۲۰۱۲ با استفاده از این شتابدهنده کشف شد. چند سال پس از کشف این ذره، شتابدهنده به منظور کشف فیزیک فراتر از هیگز، ارتقا داده شد.
جدول تناوبی را به دقت نگاه کنید. این جدول از الگوی مشخصی پیروی میکند. اگر عمیقتر نگاه و به اعداد نوشته شده در این جدول دقت کنید، به این نکته پی خواهید برد که چیزی فراتر از عنصرهای نوشته شده در جدول تناوبی وجود دارند. معادله دیراک نیز از این لحاظ، شبیه جدول تناوبی است. شاید فیزیکدانهای نظری با دقت به این معادله، به فیزیکی فراتر از مدل استاندارد پی ببرند. به معادله دیراک و عبارتهای نوشته شده برای نیروهای الکترومغناطیسی، هستهای قوی و ضعیف دقت کنید:
معادله اول در رابطه بالا، نیروی الکترومغناطیسی را توصیف میکند. این معادله شبیه معادلههای نوشته شده برای نیروهای هستهای ضعیف و قوی است، جز آنکه با حروف انگلیسی متفاوتی نوشته شدهاند. کمی به این سه معادله دقت کنید. شاید آنها سه نیروی جداگانه نباشند، بلکه یک نیرو باشند که از دو زاویه متفاوت به آنها نگاه میکنیم. نکته جالب دیگری نیز وجود دارد. این معادلهها، معادلههای ۱۲ میدان ماده در کیهان هستند. هر کدام از آنها از معادله یکسانی (معادله دیراک) پیروی میکنند. بنابراین، شاید این ۱۲ میدان با یکدیگر تفاوتی نداشته باشند و دلیل تفاوت آنها، نگاه از زاویههای مختلف باشد. یکی کردن نیروها و ۱۲ میدان کوانتومی در نظریهای به نام نظریه وحدت بزرگ، گنجانده میشود. حتی ماده و نیرو نیز میتوانند مفهوم یکسانی داشته باشند. بنابراین، معادله دیراک را شاید بتوان به معادلهای واحد برای نیروها و ۱۲ میدان ماده، تبدیل کرد. یکی از اهداف شتابدهنده هادرون، نشان دادن درستی نظریه وحدت بزرگ است.
تاکنون با مفهوم نظریه میدان های کوانتومی آشنا شدیم. جرقه این نظریه برای نخستین بار توسط مایکل فارادی به هنگام کشف میدان های الکتریکی و مغناطیسی، زده شد. بر طبق این نظریه، مفهومی به نام ذره وجود ندارد. در ادامه، مفهوم ذره در این نظریه میدان های کوانتومی را با دقت بیشتری توضیح میدهیم و همچنین، این نظریه را با جزییات بیشتری بررسی میکنیم.
مفهوم ذره در نظریه میدان های کوانتومی
در نظریه میدان های کوانتومی به ارتعاشات مشخصی از میدان، ذره گفته میشود. برای درک عمیقتر این جمله، ابتدا باید با مفاهیم زیر آشنایی داشته باشیم:
- توصیف ارتعاش و موج
- توصیف کوانتومی موج و ارتعاش
- میدان و میدان کوانتومی
با درک مفاهیم بالا، مفهوم ذره را به خوبی درک خواهیم کرد.
قانون هوک
در ابتدا، ارتعاش و نوسان را با استفاده از قانون هوک توضیح میدهیم. «رابرت هوک» (Robert Hooke) در قرن هفدهم میلادی، در مورد رابطه نیروی وارد بر فنر و مقدار کشش آن، تحقیق کرد. فنری را با طول در نظر بگیرید و جرم m را به انتهای آن وصل کنید. اکنون، جرم m را به اندازه x بکشید. از آنجا که فنر تمایل دارد به طول اولیه خود بازگردد، نیروی F بر جرم m وارد میشود و فنر را به حالت تعادل خود بازمیگرداند. هوک به این نتیجه رسید که نیروی بازگرداننده F به صورت خطی متناسب با طول کشیدگی فنر، x، است.
اگر طول کشیدگی فنر دو برابر شود، نیروی بازگرداننده وارد بر جرم m نیز، دو برابر خواهد شد. علامت منفی در تناسب بالا نشاندهنده چیست؟ علامت منفی نشان میدهد که نیروی بازگرداننده و x، در خلاف جهت یکدیگر هستند. تناسب فوق، با قرار دادن ثابتی به نام ثابت فنر به تساوی تبدیل میشود. رابطه مربوط به قانون هوک در زیر آورده شده است.
فنر را به اندازه x میکشیم و آن را رها میکنیم. نیروی بازگرداننده وارد بر فنر به جرم m شتابی برابر a میدهد. بر طبق قانون دوم نیوتن، نیرو و شتاب از طریق رابطه زیر به یکدیگر مربوط میشوند:
با قرار دادن به جای F در رابطه هوک، داریم:
با توجه به رابطه بهدست آمده برای شتاب، داریم:
به حرکتی که در آن شتاب حرکت جسم با جابجایی آن به صورت خطی با یکدیگر، ولی در خلاف جهت هم، تغییر میکنند، حرکت هارمونیک ساده گفته میشود. این حرکت در بسیاری از سیستمهای ارتعاشی فیزیکی مشاهده میشود. برای درک بهتر حرکت هارمونیک ساده، معادله آن را به صورت معادله دیفرانسیلی درجه دو مینویسیم. معادله حرکت هارمونیک ساده به صورت زیر نوشته میشود:
شتاب حرکت جسم به صورت مشتق سرعت نسبت به زمان تعریف میشود:
همچنین، سرعت حرکت جسم برابر مشتق مکان نسبت به زمان است:
با ترکیب دو تعریف بالا برای شتاب و سرعت با یکدیگر، داریم:
رابطه بهدست آمده برای شتاب را در معادله هوک قرار میدهیم:
حل معادله بالا به ما نشان میدهد که چگونه جابجایی فنر با زمان تغییر میکند. به منظور فهمیدن چگونگی جابجایی فنر با زمان به تصویر زیر توجه کنید. جسمی را به انتهای فنری متصل و رها میکنیم. فنر به همراه جسم آزادانه نوسان میکنند. با رسم جابجایی فنر بر حسب زمان، نمودار آشنایی مشاهده خواهیم کرد. بله، نمودار جابجایی فنر بر حسب زمان همان نمودار است.
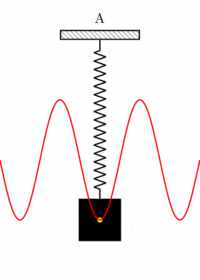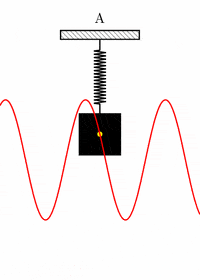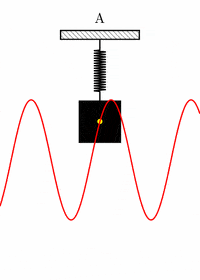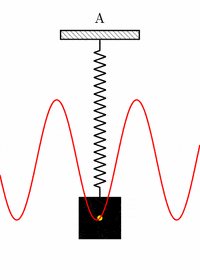
بنابراین، جابجایی فنر به صورت زیر نوشته میشود:
رابطه فوق را به صورت کلیتر زیر مینویسیم:
در رابطه بالا:
- دامنه جابجایی یا حداکثر میزان جابجایی فنر است.
- فرکانس زاویهای است و برحسب رادیان اندازه گرفته میشود.
رابطه جابجایی فنر را حدس زدیم، اکنون باید درستی آن را با قرار دادن در معادله دیفرانسیلی نوشته شده برای قانون هوک، بررسی کنیم. برای انجام این کار، ابتدا از دوبار مشتق میگیریم و آن را در سمت راست معادله و سپس، را در سمت چپ معادله، قرار میدهیم و دو سمت را با یکدیگر مقایسه میکنیم.
بنابراین، با جایگزینی و در رابطه هوک، داریم:
با حذف از طرفین رابطه بالا داریم:
بنابراین، رابطه نوشته شده برای به شرطی پاسخ معادله درجه دوم هوک است که فرکانس زاویهای با ثابت فنر و جرم متصل به آن به صورت بالا، رابطه داشته باشد. اما این شرط چه چیزی به ما میگوید؟ به این نکته توجه داشته باشید که فرکانس زاویهای به صورت زیر نیز نوشته میشود:
با مساوی قرار دادن دو رابطه نوشته شده برای فرکانس زاویهای داریم:
به رابطه بهدست آمده برای فرکانس نوسان فنر دقت کنید. به راحتی و تنها با دانستن ثابت فنر و جرم متصل به آن میتوانیم فرکانس و دوره تناوبِ حرکت نوسانی ساده را بهدست آوریم.
قدم بعدی بهدست آوردن انرژی فنر نوسانکننده است. انرژی کل سیستم برابر مجموع انرژیهای جنبشی (حرکت فنر) و پتانسیل (کشیدگی یا فشردگی فنر) است.
از آنجا که ، انرژی فنر به صورت زیر نوشته میشود:
به رابطه بهدست آمده برای انرژی دقت کنید. جابجایی فنر و سرعت آن تابع زمان هستند، اما انرژی مستقل از زمان و مقدار آن ثابت است. انرژی کل حرکت نوسانی ساده در فیزیک کلاسیک به فرکانس، دامنه و جرم جسمِ متصل به فنر بستگی دارد. بنابراین، هر مقداری میتواند داشته باشد. در ادامه، این سیستم را در مقیاس کوانتومی بررسی میکنیم.
حرکت نوسانی ساده در فیزیک کوانتوم
انرژی در فیزیک کوانتوم، گسسته است، یعنی هر مقداری را نمیتوان به آن نسبت داد. اگر فرکانس حرکت نوسانی سادهای برابر باشد، انرژی نوسانکننده به صورت زیر نوشته میشود:
در رابطه فوق:
- مقدار برابر ۰، ۱، ۲ و ... است.
- ثابت پلانک است.
- فرکانس نوسان فنر یا نوسانکننده است.
بنابراین، هر مقداری را نمیتوان به انرژی کوانتومی نسبت داد.

نوسانگر هارمونیک ساده در فیزیک کوانتوم نمیتواند با هر دامنهای نوسان کند، بلکه دامنه آن مقدارهای گسسته و مشخصی دارد. برای درک بهتر این موضوع، انرژی نوسانگر هارمونیک ساده در فیزیک کلاسیک را با مقدار آن در فیزیک کوانتوم با یکدیگر مقایسه کنید.
انرژی نوسانگر هارمونیک ساده در فیزیک کلاسیک:
انرژی نوسانگر هارمونیک ساده در فیزیک کوانتوم:
با ترکیب دو رابطه بالا، داریم:
تساوی فوق را برحسب A مرتب میکنیم:
با توجه به رابطه بهدست آمده برای دامنه نوسان، مقدار آن تنها با تغییر میکند. بنابراین، نوسانگر کوانتومی با هر دامنهای نمیتواند نوسان کند. سوالی که ممکن است مطرح شود آن است که چرا این موضوع را در زندگی روزمره مشاهده نمیکنیم. زیرا تغییرات دامنه نوسان با به قدری کوچک است که متوجه تفاوت آن نمیشویم. به بیان دیگر، فیزیک کوانتوم فیزیک حاکم بر سیستمهای میکروسکوپی است.
اصل عدم قطعیت هایزنبرگ یکی از اصلهای مهم در فیزیک کوانتوم است. بر طبق این اصل، مکان و سرعت ذره را نمیتوان همزمان تعین کرد. به عبارت دیگر، با دانستن مکان یک جسم، اطلاعی در مورد سرعت حرکت آن نداریم و برعکس، با دانستن سرعت حرکت آن، اطلاعی در مورد مکان جسم نخواهیم داشت. در فیزیک کلاسیک، اگر فنر ساکنی کشیده یا فشرده نشده باشد، انرژی کل آن برابر صفر است. این بدان معنا است که مکان و سرعت ذره همزمان صفر هستند. اما در فیزیک کوانتوم و بر طبق اصل عدم قطعیت هایزنبرگ، تعیین همزمان سرعت و مکان ذره امکانپذیر نخواهد بود. در نتیجه، حتی زمانی که فنر، ساکن و در حالت تعادل خود قرار داشته باشد، حرکتِ تلاطمی کوانتومی ذاتی در فنر وجود دارد. برای درک بهتر این مفهوم، عدم قطعیت در انرژی را برای نوسانگر هارمونیک کوانتومی بهدست میآوریم. ابتدا، انرژی نوسانگر را به صورت زیر مینویسیم:
عدم قطعیت در مکان و تکانه را بهدست میآوریم و در رابطه بالا قرار میدهیم:
از انرژی نسبت به مشتق میگیریم و آن را نسبت به کمینه میکنیم.
عدم قطعیت در مکان نوسانگر به صورت زیر نوشته میشود:
با جایگزینی رابطه فوق در رابطه بهدست آمده برای عدم قطعیت انرژی، داریم:
بنابراین، کمینه انرژی نوسانگر هارمونیک کوانتومی برابر است. به این عدد، انرژی نقطه صفر گفته میشود و نتیجه بسیار مهمی در فیزیک کوانتوم است. از اینرو، انرژی کوانتومی نوسانگر هارمونیک کوانتومی به صورت زیر نوشته میشود:
تاکنون با حرکت نوسانی در فیزیک کلاسیک و کوانتوم آشنا شدیم. در ادامه، در مورد حرکت موجی و ارتعاش صحبت خواهیم کرد.
حرکت موجی
به انتشار اختلال، همراه با انتقال اطلاعات و انرژی از یک مکان به مکان دیگر، موج گفته میشود. معادله موج در حالت کلی به صورت زیر نوشته میشود:
اگر در نقطهای با مقدار ثابت x تمرکز کنیم ()، معادله جابجایی فوق به شکل تابع مکانِ نوسانگر هارمونیک ساده نوشته خواهد شد:
بنابراین، موج را میتوان به صورت یک سری از نوسانگرهای هارمونیک جفت شده در نظر گرفت. در مطالب بالا، معادله حرکت نوسانگر هارمونیک ساده را بهدست آوردیم. این معادله مشابه معادله موج است:
به طور مشابه، با محاسبه مشتق دوم y نسبت به زمان و مکان و جایگذاری آن در معادله موج میتوان درستی پاسخ حدس زده شده را بررسی کرد. پاسخ به شرطی صحیحی است که سرعت حرکت موج با استفاده از رابطه زیر بهدست آید:
معادله موج پیشبینی میکند که تمام موجها با سرعت یکسان حرکت میکنند. همچنین، طول موج، فرکانس، و دامنه موج میتوانند هر مقداری داشته باشند. قبل از آنکه در مورد موج کوانتومی صحبت کنیم، خالی از لطف نیست که معادله موج را کمی بهبود ببخشیم.
معادله موج اصلاح شده
برای اصلاح معادله موج، عبارتی خطی بر حسب y به آن اضافه میشود. بنابراین، معادله اصلاح شده موج به شکل زیر درمیآید:
عبارت را در معادله اصلاح شده موج قرار میدهیم. این عبارت به شرطی در معادله اصلاح شده موج صدق میکند که شرط زیر برقرار باشد:
با توجه به آنکه و ، داریم:
رابطه فوق را برحسب فرکانس مینویسیم:
اگر برابر صفر باشد، به رابطه بین فرکانس، طول موج و سرعت در معادله اصلاح نشده موج میرسیم. نکته بسیار جالبی در مورد رابطه نوشته شده برای فرکانس موج اصلاح شده وجود دارد. مجذور در زیر رادیکال همواره مثبت است، بنابراین کمترین مقدار فرکانس برابر خواهد بود. در نتیجه، با اصلاح معادله موج، فرکانس از مقدار مشخصی کمتر نخواهد بود. این فرکانسِ کمینه، نقش مهمی در نظریه میدان های کوانتومی و تعریف ذره در این نظریه، ایفا میکند.
انرژی موج
طنابی را فرض کنید که جرم بر واحد طول آن برابر است. فرض کنید موجی عرضی را در طناب منتشر میکنید. از آنجا که موج عرضی است، جابجایی طناب بر جهت انتشار موج عمود است. بنابراین، قسمت کوچکی از طناب در راستای محور عمود، به سمت بالا و پایین حرکت میکند. انرژی جنبشی این بخش از طناب به صورت زیر نوشته میشود:
با مشتق گرفتن از مکان موج نسبت به زمان، سرعت حرکت موج در راستای عمود را بهدست میآید. با قرار دادن سرعت در رابطه انرژی، داریم:
برای نوشتن انرژی پتانسیل، قسمتی از طناب را در نظر بگیرید و کار انجام شدن به هنگام کشیدگی آن را محاسبه کنید.
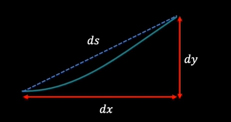
در رابطه فوق، T نیروی کشش است. از آنجا که قسمت کوچکی از طناب را در نظر گرفتهایم، عبارت را بسط میدهیم:
بنابراین، انرژی پتانسیل به شکل زیر نوشته میشود:
در ادامه، را در رابطه انرژی پتانسیل قرار میدهیم:
بنابراین، انرژی کل بخش کوچک انتخاب شده در طناب برابر است با:
انرژی کل طناب در یک طول موج به صورت زیر بهدست میآید:
با محاسبه انتگرال فوق، انرژی طناب بر واحد طول موج به صورت زیر بهدست میآید:
انرژی بر واحد طول موج در طناب متناسب با مجذور فرکانس و دامنه موج و همانند انرژی محاسبه شده برای نوسانگر هارمونیک ساده است. سوالی که ممکن است مطرح شود آن است که آیا انرژی موج در فیزیک کوانتوم از رابطه مشابهی پیروی میکند.
امواج کوانتومی
از آنجا که موج را به صورت ترکیبی از نوسانگرهای هارمونیک ساده جفت شده، تعریف کردیم، مشخصههای موج کوانتومی شباهت زیادی به نوسانگر هارمونیک کوانتومی دارد. انرژی موج کوانتومی برحسب ثابت پلانک و فرکانس نوشته میشود.
اگر مقدار n زیاد باشد، از جمله صرفنظر میکنیم. با مرتب کردن معادله فوق برحسب دامنه موج، داریم:
تاکنون، با دو نوع موج اصلاح شده و اصلاح نشده آشنا شدیم. این دو موج در جدول زیر با یکدیگر مقایسه شدهاند.
| موج اصلاح نشده | موج اصلاح شده |
| فرکانس و در نتیجه انرژی، هر مقداری میتوانند داشته باشند. | به معادله موج اصلاح شده، عبارتِ خطی اضافه شده است. |
| فرکانس موج اصلاح نشده با استفاده از رابطه بهدست میآید. | فرکانس موج اصلاح نشده با استفاده از رابطه بهدست میآید. همانطور که دیده میشود فرکانس موج اصلاح شده، مقدار کمینهای برابر دارد. |
| اگر انرژی سیستم بسیار کوچک باشد، باز هم میتوان موج کوانتومی آن را ساخت. | با اضافه کردن فیزیک کوانتوم به این معادلههای موج، این فرکانس کمینه به صورت قید در انرژی کوانتومی این نوع موج، ظاهر میشود. |
| اگر انرژی سیستم از کوچکتر باشد، نمیتوان موج کوانتومی آن را ساخت. |
تاکنون، با مفاهیم نوسانگر هارمونیک ساده، امواج و امواج کوانتومی آشنا شدیم. همچنین، گفتیم اگر به معادله اصلی موج عبارتی خطی برحسب y اضافه شود، فرکانس موج مقدار کمینهای خواهد داشت. این فرکانس کمینه نقش مهمی را در نظریه میدانهای کوانتومی ایفا میکند. در ادامه، به تعریف میدان و ذره در نظریه میدان های کوانتومی میپردازیم.
میدان چیست ؟
میدان در فیزیک تابعی از فضا و زمان است. چگونگی تغییر این تابع با فضا و زمان، توسط معادله حرکت توصیف میشود. میدانها به دو دسته کلی تقسیم میشوند:
- میدانهای نردهای: میدان نردهای عددی است که به هر نقطه در فضا اختصاص داده میشود. به عنوان مثال، اگر بخواهید دمای هر نقطه از فضا را اندازه بگیرید، به راحتی میتوانید میدانی به نام میدان دما تعریف کنید و به هر نقطه از فضا عددی را به عنوان دمای آن نقطه، اختصاص دهید. برای درک مفهوم میدان دما از نموداری به نام گرادیان دمایی استفاده میشود. در این نمودار، نقطههای قرمزرنگ، دمای بالاتری دارند. همچنین، برای درک بهتر چگونگی تغییر دما در حضور منبع گرمایی جدید یا تغییر آن میتوان از معادله گرما استفاده کرد.
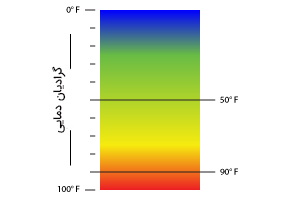
- میدانهای برداری: در این نوع میدان، به هر نقطه از فضا، اندازه و جهت، اختصاص داده میشود. به عنوان مثال، اگر بخواهید جهت و سرعت باد را در هر نقطه از فضا اندازه بگیرید، نقشهای به صورت نشان داده شده در تصویر زیر تهیه میکنید. همانطور که در تصویر مشاهده میکنید، برداری با طول و جهت مشخص در هر نقطه، رسم شده است. جهت بردار نشاندهنده جهت باد و طول بردار، تعیینکننده مقدار سرعت باد در آن نقطه است.
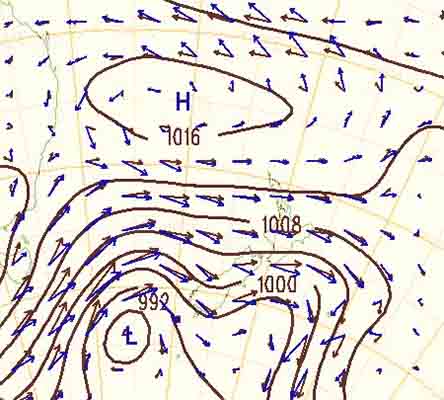
میدان الکتریکی، مثال دیگری از میدانهای برداری است. این میدان در اطراف بارهای الکتریکی به وجود می آید. در این حالت، هر بردار در هر نقطه از فضا نشاندهنده جهت و اندازه نیروی وارد بر بار الکتریکی فرضی قرار گرفته در میدان الکتریکی است. همچنین، اگر بار الکتریکی حرکت کند، خطوط میدان با توجه به موقعیت بار، تغییر خواهند کرد. اگر بار الکتریکی با شتاب مشخصی حرکت کند (به عنوان مثال، در مسیر دایرهای حرکت کند)، میدان موجدار خواهد شد. در ادامه، این موجها در فضا حرکت میکنند. به این موج، نور گفته میشود.
میدان های نسبیتی
در قرن نوزدهم میلادی، ماکسول معادلههای الکتریکی و مغناطیس را با یکدیگر ترکیب کرد و به معادلهای شبیه معادله موج رسید. او با استفاده از معادله الکترومغناطیس، سرعت حرکت موج الکترومغناطیسی را پیشبینی کرد.
نکته قابلتوجه آن است که سرعتِ نور، پیشبینی شده توسط ماکسول به خوبی توسط آزمایشهای تجربی تایید شده است. اما سوال مهمی که باید به آن پاسخ داده شود آن است که سرعت نور نسبت به چه چارچوب مرجعی اندازه گرفته میشود. این سوال توسط اینشتین در آغاز قرن بیستم میلادی پرسیده شد. او در آن زمان روی نظریه نسبیت کار میکرد.
بر طبق نظریه نسبیت اینشتین، سرعت نور از دید تمام ناظرها در تمام چارچوبها، یکسان است. بنابراین، ناظرهای مختلف، گذر زمان را متفاوت احساس خواهند کرد. همچنین، اینشتین معتقد بود که نور بدون نیاز به محیط مادی میتواند با سرعت ثابتی در خلأ حرکت کند.
موج الکترومغناطیسی، تنها مثالِ میدانهای نسبیتی نیست. با توجه به دو معادله نوشته شده برای موج، معادله اصلاح شده و اصلاح نشده، موجهای نسبیتی به دو دسته کلی تقسیم میشوند. معادلههای موج اصلاح شده و اصلاح نشده برای میدانهای نسبیتی به صورت زیر اصلاح میشوند:
معادله موج اصلاح نشده
معادله موج اصلاح شده
همانطور که در دو معادله نسبیتی بالا مشاهده میکنید، دو تغییر ایجاد شده است:
- جایگزین y شده است.
- سرعت با سرعت نور، ، جایگزین شده است.
در معادلههای نسبیتی موج، سرعت نور و میدان نسبیتی هستند. سوال اصلی آن است که این معادلهها، چه چیزی را توصیف میکنند. در حالت کلی، هر دو معادله توصیفکننده موجهایی هستند که اطلاعات و انرژی را از یک نقطه در فضا به نقطه دیگر منتقل میکنند. به این نکته توجه داشته باشید که میدان نسبیتی ویژگیهای محیط فیزیکی معمولی را توصیف نمیکند. به بیان دیگر، هیچ محیط زمینهای وجود ندارد. تا جایی که میدانیم، میدانهای نسبیتی یکی از بنیادیترین عناصر واقعیت هستند. بنابراین، فیزیکدانها به دنبال یافتن معنا و مفهوم ذرات بنیادی هستند. تنها کاری که برای این کار باید انجام شود ترکیب فیزیک نسبیت با فیزیک کوانتوم است.
برای ترکیب این دو شاخه از فیزیک، از معادله اصلاح شده موج شروع میکنیم.
همانطور که گفتیم، فرکانس این نوع موج، مقید و دارای مقدار کمینه است.
طرفین معادله بالا را به توان دو میرسانیم:
رابطه بهدست آمده شبیه رابطه فیثاغورث برای مثلثهای قائمالزاویه است و این مورد، نشانه خوبی در فیزیک است. در ادامه، رابطه فوق را با رابطه انرژی کوانتومی به ازای ، ترکیب میکنیم. برای انجام این کار، طرفین معادله فرکانس مقید را در ثابت پلانک ضرب میکنیم:
از آنجا که ، معادله فرکانس به صورت زیر نوشته خواهد شد:
اگر با نظریه نسبیت خاص اینشتین آشنایی داشته باشید، رابطه فوق شما را به یاد رابطه بین انرژی و تکانه در نسبیت خاص میاندازد.
در رابطه بالا، انرژی جرم ساکن ذره است و حتی هنگامی که ذره ساکن باشد، این انرژی وجود دارد. بنابراین، این انرژی میتواند کمینه انرژی جسم یا ذره باشد. گفتیم فرکانس موجی که از معادله موج نسبیتی اصلاح شده پیروی میکند، کمینه است. همچنین، کوانتوم این میدان، انرژی کمینهای برابر حاصلضرب ثابت پلانک در فرکانس کمینه دارد. بنابراین، مقدارهای و را میتوان مساوی یکدیگر قرار داد:
به طور مشابه، را برابر قرار میدهیم.
تساویهای فوق چه نکتهای را بیان میکنند؟ با حذف c از معادله ، به معادله معروف دوبروی میرسیم:
همچنین، معادله را برحسب جرم، مرتب میکنیم:
این معادله، جرم یک کوانتوم از این نوع میدان نسبیتی را به ما میگوید. به بیان دیگر، هر ذره جرمداری را میتوان به عنوان کوانتای میدان نسبیتی در نظر گرفت که امواج آن فرکانس کمینه و در نتیجه انرژی کمینه دارند. نکته جالبتر دیگری نیز در مورد رابطه بهدست آمده برای جرم وجود دارد. بار دیگر به این رابطه دقت کنید. بر طبق این رابطه، جرم برابر نسبت کمینه انرژی ارتعاش میدان کوانتومی بر مجذور سرعت نور است. در مورد ذرات بدون جرم چه میتوان گفت؟

ذرات بدون جرم
به رابطه بهدست آمده برای جرم دقت کنید:
اگر فرکانس کمینه را برابر صفر قرار دهیم، جرم نیز صفر خواهد شد. به یاد بیاورید که در معادله موج اصلاح نشده، فرکانس کمینهای وجود نداشت. نور که از ذرات بدون جرمی به نام فوتون تشکیل شده است، توسط معادله اصلاح نشده موج توصیف میشود. بنابراین، هنگامی که فرکانس کمینه را برابر صفر قرار دهیم، نهتنها جرم برابر صفر میشود، بلکه به معادله اثر فوتوالکتریک میرسیم. تمام مطالب گفته شده تا اینجا برای آن بود که ذره را در نظریه میدان های کوانتومی تعریف کنیم.
ذره بنیادی، کوچکترین ارتعاش ممکن (کوانتوم) یک میدان کوانتومی نسبیتی است. ذرات جرمدار توسط معادله موج اصلاح شده توصیف میشوند. در مقابل، معادله اصلاح نشده موج، توصیفکننده ذرات بدون جرم است. این دیدگاه در قلب مدل استاندارد ذرات بنیادی قرار دارد. در این چارچوب، میدان کوانتومی مفهومی بنیادی است و ذرات آشنای مدل استاندارد به صورت کوانتای این میدان در نظر گرفته میشوند. به عنوان مثال، به کوچکترین ارتعاش در میدان الکترون، الکترون میگوییم. به طور مشابه، کوچکترین ارتعاش در میدان الکترومغناطیسی، فوتون و کوچکترین ارتعاش در میدان کوارک، کوارک است. بنابراین، هر ذره کوچکی در کیهان، به عنوان موج کوچک کوانتومی در میدان نسبیتی در نظر گرفته میشود.
اکنون میدانیم ذره در نظریه میدان های کوانتومی چگونه تعریف میشود، اما هنوز سوالهای بسیاری باقی ماندهاند.
- چه چیزی فرکانس کمینه معادله موج اصلاح شده را تعیین میکند؟
- چرا برخی ذرات جرمدار و برخی از آنها بدون جرم هستند؟
- چگونه میدان کوانتومی مشخصی با میدانهای دیگر برهمکنش میکند؟
- رابطه بین ماده و ضدماده چیست؟
بررسی شهودی نظریه میدان های کوانتومی
در مطالب بالا با تعریف ذره در نظریه میدان های کوانتومی آشنا شدیم. در طبیعت ذره گاهی ظاهر و گاهی ناپدید میشود. به عنوان مثال، فوتون پس از جذب توسط اتم، ناپدید میشود. فیزیک کوانتوم با هر ذره رفتار مستقلی دارد، اما در گروهی از ذرات، مانند الکترونها، تمام آنها ویژگی و رفتار یکسانی را از خود نشان میدهند. چگونه جرم و بار الکترونی که در فاصله بسیار دور از زمین قرار دارد، برابر جرم و بار الکترونِ داخل سیب است؟ نظریه میدانهای کوانتومی به این پرسش پاسخ میدهد.
همانطور که گفتیم این نظریه از ترکیب دو شاخه از فیزیک ساخته میشود:
- نظریه نسبیت خاص
- فیزیک کوانتوم
در نخستین گام، جهان را تهی در نظر میگیریم. بر طبق نظریه نسبیت اینشتین، تاروپود کیهان از فضا و زمان تشکیل شده است. برای سادگی، فضا را دوبعدی در نظر بگیرید و زمان را به عنوان بعد سوم به آن اضافه کنید.
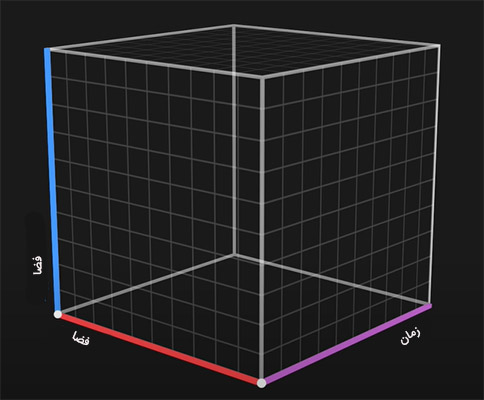
در ادامه، میخواهیم جهان را با ماده پر کنیم. گفتیم ذرات قرار گرفته در یک گروه، کاملا یکسان هستند. الکترونها، نقاط موضعی جسمی بنیادی به نام میدان هستند که در سراسر جهان پخش شده است. بنابراین، برای ساخت جهان، ابتدا باید میدانها را به آن اضافه کنیم. در مطالب بالا میدان را تعریف و انواع آن را بیان کردیم. گفتیم میدان همانند سیالی است که فضا و زمان را پر میکند. هر نقطه از میدان، توسط جسمی ریاضی، اشغال شده است. میدانها میتوانند از اعداد، بردارها یا هر جسم عجیب و غریب دیگری تشکیل شده باشند.
نسبیت خاص، محدودیتهای مشخصی اعمال میکند و ما را مجبور میکند به تقارنهای مشخص و مطابق با هندسه فضا-زمان، احترام بگذاریم.
- تقارن انتقال
- تقارن چرخش
- تقارن تغییر چارچوب مرجع
تنها برخی اجسام ریاضی به این تقارنها احترام میگذارند و آنها را تحت عنوان اسپین میشناسیم.
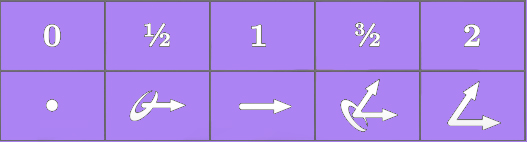
اعداد سادهترین مفهوم استفاده شده است. اسپین اعداد برابر صفر است، زیرا اگر فضا را به دور عددی بچرخانیم، مقدار آن تغییر نخواهد کرد. بردارها نشاندهنده جهت در فضا هستند. جهت بردار، به جهت مشاهده آن بستگی دارد. اسپین بردار برابر یک است، زیرا وقتی فضا را به اندازه ۳۶۰ درجه بچرخانیم، بردار نیز همراه فضا، یک دور کامل میچرخد. اجسام عجیبتری در نسبیت وجود دارند. یکی از آنها «اسپینر» (Spinor) با اسپین است. اگر فضا را یک دور کامل بچرخانیم، اسپینر به شکل اولیه خود بازنمیگردد و پس از دو دور چرخش کامل فضا، اسپینر به شکل اولیه خود بازمیگردد.
گرچه این اجسام ریاضی به طور کامل انتزاعی به نظر میرسند، اما تمام آنها از تقارنهای نسبیتی پیروی میکنند. بنابراین، کاندیداهای بالقوهای برای پر کردن جهان تهی هستند. علاوه بر اعمال محدودیت بر اجسام مجاز به هنگام پر کردن جهان، تقارنهای فضا-زمان نیز محدودیتهایی را در مورد نوع رفتار اجسام داخل میدانها، قرار میدهند. هر تقارن، میدان را مجبور میکند پایستگی کمیتهای مشخصی را در طول زمان، حفظ کند. این پایستگی عبارت هستند از:
- پایستگی انرژی
- پایستگی تکانه
- پایستگی تکانه زاویهای
- پایستگی سرعت مرکز جرم
همچنین، اجسام ریاضی نیز تقارنهای مخصوص به خود دارند. به عنوان مثال، اگر میدانی از اعداد مختلط را تشکیل دهیم، تقارنی داخلی را مشاهده خواهیم کرد. این تقارن، پایستگی کمیت دیگری به نام بار الکتریکی را در طول زمان نشان میدهد.
تا اینجا، فضا-زمانی پر شده از میدان داریم. این میدان از تمام محدودیتهای اعمال شده توسط نسبیت خاص پیروی میکند. اما هدف ما توصیف جهان میکروسکوپی است. برای انجام این کار، میدان را به میدان کوانتومی تبدیل میکنیم. برای آنکه جسمی را از فیزیک کلاسیک به فیزیک کوانتوم منتقل کنیم، تابعی به نام توزیع احتمال به آن نسبت میدهیم. در این صورت، به جای مشخص کردن مکان دقیق جسم، مکان آن را با احتمال مشخصی، تعیین میکنیم. به طور مشابه، به هنگام تبدیل میدان کلاسیک به میدان کوانتومی، به میدان کلاسیک اجازه میدهیم پیکربندیهای متفاوتی داشته باشد.
هنگامی که میدان از فیزیک کلاسیک به فیزیک کوانتوم منتقل میشود، ویژگی بسیار جالبی بهدست میآورد. همانطور که الکترون در اتم، ترازهای انرژی مشخصی دارد، ترازهای انرژی میدان کوانتومی نیز گسسته و دارای مقدارهای مشخصی است. این انرژیهای کوانتومی میتوانند ظاهر یا ناپدید شوند. ترازهای انرژی میدان همان ذرات هستند. با تعریف دقیق ذره در نظریه میدان کوانتومی آشنا شدیم. سنگی را در برکه آبی بیندازید و به انتشار موج در سطح آب دقت کنید. ذره نیز موج یا اختلالی در میدان کوانتومی است که در آن پخش میشود. علاوه بر ذرات واقعی، ذرات مجازی نیز در میدان کوانتومی وجود دارند. این ذرات به صورت نوساناتی در میدان هستند که به وجود میآیند و بلافاصله از بین میروند. مدت زمانی که ذرات مجازی وجود دارند به اندازهای کوتاه است که مشاهده آنها به طور عملی ممکن نیست.
ساخت جهان را قدم به قدم ادامه میدهیم تا به جهان واقعی نزدیک شویم. تاکنون فضا-زمان را از میدان کوانتومی متشکل از ذرات واقعی و مجازی، پر کردهایم. در جهان، میدانهای کوانتومی مختلفی، همزمان وجود دارند. در این میدانها، گروههای مختلفی از ذرات قرار گرفتهاند.
- برخی از میدانها، میدانهای برداری و اسپین آنها برابر یک است. ذراتی مانند فوتون، بوزونهای Z، بوزونهای Z و گلوئونها در این میدانها قرار دارند.
- برخی از میدانها، میدانهای اسپینر و اسپین آنها برابر است. اسپینرها همان فرمیونها و سازنده ماده هستند. الکترونها، میونها، ذرات تاو و نوترینوها، مثالهایی از فرمیونها هستند.
- در پایان، میدانی با اسپین صفر، به نام میدان هیگز، وجود دارد.
برخی از میدانها، تقارن داخلی دارند. این تقارن میتواند مشخصهای به میدان بدهد که در طول زمان، پایسته باقی بماند. گفتیم میدانهای تشکیل شده از اعداد موهومی، تقارنی دارند که به آنها بار الکتریکی میدهد. این تقارن، ذرات را به دو دسته کلی تقسیم میکند:
- ذرات با بار مثبت
- ذرات با بار منفی
میدانهای دیگر نیز تقارنهای عجیب بیشتری دارند. به عنوان مثال، میدان کوارک تقارنی دارد که به کوارکها بار دیگری به نام بار رنگی، نسبت میدهد. بار رنگی نیز در طول زمان پایسته باقی میماند. این بار، کوارکها را به سه دسته کلی تقسیم میکند:
- کوارکهای قرمز
- کوارکهای آبی
- کوارکهای سبز
چیدمان تمام این میدانهای تشکیلدهنده جهان در کنار یکدیگر، مدلی به نام مدل استاندارد ذرات بنیادی را میسازد. تا امروز، این مدل یکی از موفقترین مدلها برای توصیف جهان میکروسکوپی است. تا اینجا، جهانی که ساختهایم تمام ذرات جهان واقعی را دارد، اما هنوز با آن تفاوت زیادی دارد. محدودیتهای فضا-زمان، ذرهها را به حرکت روی خط راست مجبور میکند. برای کامل کردن جهانی که ساختهایم، تنها کافی است جزء دیگری به آن اضافه کنیم. در واقع، باید به میدانها اجازه دهیم که با یکدیگر برهمکنش داشته باشند.
برای درک بهتر این موضوع، سادهترین برهمکنش، یعنی برهمکنش بین میدان فوتون و میدان الکترون را در نظر بگیرید. به الکترون اجازه میدهیم که فوتونی مجازی را جذب یا تابش کند. این مورد در مورد فوتون نیز صدق میکند. وقوع این برهمکنش ساده، عواقب شدیدی به دنبال دارد. دو الکترون ساکن را در نظر بگیرید. در طی زمان، الکترونها به سمت آینده پیش میروند.
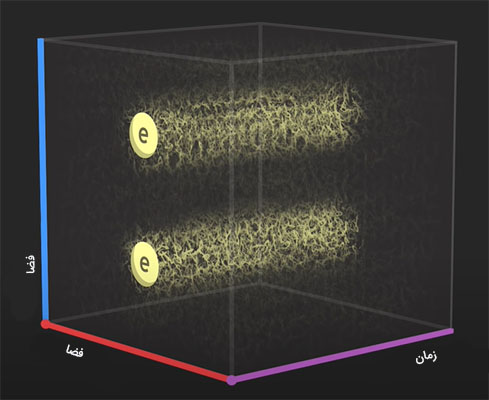
در ابتدا، اینگونه به نظر میرسد که دو الکترون تا بینهایت ساکن باقی میمانند. اما نباید فراموش شود که الکترونها به طور پیوسته در میدان فوتون در حال حرکت هستند. بنابراین، با میدان فوتون برهمکنش دارند. در مطالب بالا دیدیم که میدان کوانتومی، همزمان متوجه تمام تغییر شکلها میشود. هر تغییر شکل بیانگر داستانی منحصربهفرد است و در برخی از این داستانها، الکترون با میدان فوتون برهمکنش میکند. به عنوان مثال، در یکی از داستانها، فوتونی مجازی توسط یکی از الکترونها تابش میشود. این فوتون، قسمتی از تکانه الکترون را با خود حمل میکند. پس از مدت زمان مشخصی، این فوتون توسط الکترون دیگر جذب میشود.
در داستانی دیگر، دو فوتون، بین الکترونها مبادله میشوند. حالت سوم، داستان پیچیدهتری دارد. در این حالت، یکی از الکترونها، فوتونی مجازی تابش میکند. در ادامه، فوتون تابیده شده به الکترون و پوزیترون مجازی تبدیل میشود. در ادامه، پوزیترون و الکترون تولید شده، نابود و به فوتون تبدیل میشوند. در پایان، فوتون ایجاد شده توسط الکترون دوم جذب میشود. تبادل تکانه بین دو الکترون توسط ذرات مجازی انجام میشود. در برخی داستانها، دو الکترون به یکدیگر نزدیک و در برخی دیگر، از هم دور میشوند. به مثال مشابهی توجه کنید.
سیمهای گیتار میتوانند با فرکانسهای مختلفی ارتعاش کنند. هر فرکانس، صدای منحصربهفردِ خود را دارد. آهنگ ایجاد شده در گیتار به دلیل برهمنهی تمام این فرکانسها با یکدیگر، است. حالت مشابهی نیز برای میدان کوانتومی رخ میدهد. برهمنهی هر یک از داستانهای گفته شده برای میدان کوانتومی با یکدیگر، سیر تکاملی سیستم فیزیکی را توصیف میکند. در مثال دو الکترون، با قرار دادن تمام داستانها در کنار یکدیگر مشاهده میکنیم که دو الکترون از یکدیگر دور میشوند. هر یک از الکترونها به دلیل تبادل فوتونهای مجازی با الکترون دیگر، احساس میکند که نیرویی از نوع دافعه به آن وارد میشود. این نیروی دافعه همان نیروی الکترومغناطیس است. اگر به جای دو الکترون، یک الکترون و یک پوزیترون را در نظر میگرفتیم، نتیجه متفاوتی بهدست میآمد. در این حالت، برهمنهی داستانهای مختلف سبب نزدیک شدن الکترون و پوزیترون به یکدیگر و نیروی جاذبه میشود.
سوالات جالب در مورد نظریه میدان های کوانتومی
تاکنون با نظریه میدان های کوانتومی آشنا شدیم. در ادامه، سوالات جالبی را در این زمینه پاسخ میدهیم.
ذره و پادذره در میدان کوانتومی چگونه تعریف میشوند ؟
ذره و پادذره هر دو ارتعاشات ایجاد شده در میدان یکسانی هستند. این ارتعاشات یکسان، اما در دو جهت مخالف رخ میدهند.
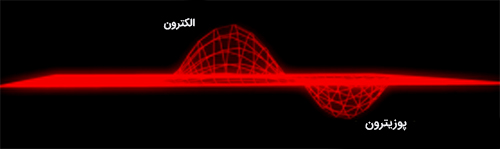
در فیزیک کوانتوم، ذرات گسسته در نظر گرفته میشوند، در حالیکه در نظریه میدان های کوانتومی، ذرات به صورت نوسان در میدان کوانتومی تعریف میشوند. از آنجا که میدان پیوسته است، چه پاسخی برای این تناقض ایجاد شده وجود دارد؟ به این نکته توجه داشته باشید که این نوسانها در انرژیهای خاصی رخ میدهند. این انرژی توسط جرم ذره تعیین میشود. به بیان دیگر، جرم، انرژی لازم برای نوسان میدان است. بر طبق رابطه معروف اینشتین، یعنی ، انرژی و جرم معادل یکدیگر هستند. میدانها، تنها انرژیهایی برابر یا بیشتر از جرم سکون ذره را میپذیرند.
میدان کوانتومی، انرژیهای کمتر از انرژی آستانه را قبول نمیکند. اما اگر ضربه محکمی به میدان وارد کنیم، ذره ایجاد خواهد شد. به واحد گسسته انرژی که میدان میپذیرد، جرم سکون ذره گفته میشود. برای خلق ذرهای مشخص، این مقدار انرژی باید به میدان اضافه شود. به عنوان مثال، الکترون هنگامی ایجاد میشود که میدان الکترون با انرژی برابر 0/511 مگا الکترونولت، تحریک شود. این عدد، جرم الکترون است. اگر انرژی برابر ۰/۴ مگا الکترونولت را به میدان اضافه کنیم، هیچ الکترونی ایجاد نخواهد شد. اگر انرژی برابر ۱/۱ مگا الکترونولت به میدان اضافه شود، دو الکترون به وجود خواهند آمد. این مورد برای تمام ذرات بنیادی صحیح است.
نظریه میدان های کوانتومی به چه سوالاتی پاسخ نمی دهد ؟
هنوز سوالات بسیاری وجود دارند که حتی نظریه میدان های کوانتومی نیز، تاکنون پاسخی برای آنها نداشته است:
- انرژی تاریک چیست؟
- بیگبنگ چگونه رخ داد؟
- چرا در کیهان، مقدار ماده بیشتر از ضدماده بیشتر است؟
چگونه می توان تابع توزیع احتمال در فیزیک کوانتوم را به موج های نوسانی در میدان کوانتومی ربط داد ؟
بارها در مسائل فیزیکی با این جمله مواجه شدهاید، الکترونی در مکان x قرار دارد و با سرعت حرکت میکند. بیان این جمله در فیزیک کوانتوم اشتباه است. دلیل اشتباه بودن این جمله آن نیست که نمیتوانیم سرعت یا مکان الکترون را اندازه بگیریم، بلکه چیزی به نام موقعیت مکانی یا سرعت وجود ندارد. تمام این مفاهیم در تابعی به نام تابع موج نهفته شده است. این تابع در تمام فضا پخش میشود و تنها به هنگام اندازهگیری موقعیت مکانی یا سرعت ذره، اطلاعاتی در مورد آنها به ما میدهد. به عنوان مثال، شکل میدان الکترومغناطیسی بیانگر تابع موج فوتونها یا شکل میدان الکترون، نشاندهنده تابع موج الکترونها است. تابع موج مفهومی است که وجود دارد. هنگامی که الکترونی را مشاهده میکنید، تابع موج آن را نمیبینیم زیرا تابع موج از بین رفته و به مقدارهای گسسته تبدیل شده است. این تبدیل، توسط معادله موج شرودینگر پیشبینی میشود.
چه کسی میدان را کشف کرد ؟
مایکل فارادی برای نخستین بار از کلمه میدان استفاده کرد و در سال ۱۸۸۴ این کلمه را در دفترچه یادداشت خود نوشت.
جمعبندی
در این مطلب، در مورد نظریه میدان های کوانتومی صحبت کردیم. جهان را میتوان به صورت جعبهای در نظر گرفت که فضا-زمان محورهای آن هستند. در این جعبه دو میدان به نامهای میدان الکترون و میدان الکترومغناطیسی، قرار دارند. در داخل هر یک از این میدانها، بستههای کوچک انرژی به نام ذره، ظاهر و ناپدید میشوند. ماهیت میدانهای الکترون و الکترومغناطیسی بسیار متفاوت است و اجسام ریاضی تشکیلدهنده این میدانها تفاوت زیادی با یکدیگر دارند. به عنوان مثال، میدان الکترون از اسپینرها ساخته شده است. بزرگترین دستاورد علم فیزیک در اوایل قرن بیستم میلادی با ترکیب نسبیت خاص و فیزیک کوانتوم و طرح نظریه میدان های کوانتومی، رخ داد. طرح این نظریه، سبب پیدایش شاخههای دیگری از فیزیک، مانند الکترودینامیک کوانتومی و مدل استاندارد ذرات بنیادی، شد.













سلام. بسیار عالی و با زبانی ساده نوشته شده است . واقعا دست نویسنده درد نکند. موضوعی که در عین پیچیدگی با زبان ساده بیان شده است .
سلام وقت به خیر. خیلی ممنونم بابت مقاله مفیدتون.
ببخشید یه سوالی داشتم فرمودید ذرات از ارتعاشات امواج در میدان کوانتمی به وجود میاد . سوالم این بود خود این امواج داخل میدان کوانتومی چگونه درست شده اند ؟
ذرات از ارتعاشات امواج بوجود نمی آیند. در واقع ارتعاشات، نتیجه برهمکنش امواج روی ذرات است. اما بر اساس نظریه میدان، نوسانات مشخص یک میدان(لطفا توجه شود که نوسانات مشخص) منجر به تولید ذره خواهد شد و کمترین فرکانس این نوسان تناظر با جرم سکون ذره است.
با سلام خدمت شما؛
نکته بیان شده صحیح است و اصلاحات لازم در ابتدای بخش «مفهوم ذره در نظریه میدان های کوانتومی» اعمال شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
درود
خانم یوسفی ، مقالات شما در فرادرس از بهترین هاست. خیلی ممنون
با سلام؛
از اینکه مطالعه این مطلب برای شما مفید بوده خرسندیم و از همراهی شما با مجله فرادرس سپاسگزاریم،
با تشکر
باسلام.
در اوایل مقاله شما اومدید معادله ذرات بنیادی رو نشونمون دادید.
همون معادلهای که محدودیت علم فیزیکه.و قسمتای مختلف معالهرو معرفی کردید.
اما اون طرف خود معادله،
اون طرف مساوی،
یهZ بود که اصلا توضیحش ندادید.
ولی سوال من این بود که اکه تمام قسمتای معاله نظریه استاندارد رو یه روزی درک کنیم و حل بشه به چه چیزی میرسیم؟
در اول مقاله گفته شده الکترون پروتون و نوترون از اجزای جداگانه درست شده اند،،،برای الکترون این گزاره درست نیست خواهشاً اصلاح بفرمایید 🙏
مقاله خوبی بود سپاسگزارم 🙏
با سلام،
مقاله بازبینی و اصلاح شد.
با تشکر از همراهی شما با مجله فرادرس
با سلام؛
هدف از حل این معادله رسیدن به نظریه وحدت بزرگ است،
با تشکر از همراهی شما با مجله فرادرس
سلام وقت شما بخیر.
این مقاله واقعا خوب بود من که خیلی لذت بردم.
امیدوارم منم از تاثیرگذارترین افراد توی فیزیک در آینده باشم. و فیزیکدان بشم.
و این هدفمه.
اما به دلایلی برای رسیدن به مسیر فیزیکدانی مسیرم خیلی سخت شده.
در کل مقالهتون خیلی خوب بود.
با تشکر.
با سلام؛
از اینکه مطالعه این مطلب برای شما مفید بوده خرسندیم و از همراهی شما با مجله فرادرس سپاسگزاریم،
با تشکر