اثر فوتوالکتریک (Photoelectric Effect) + دانلود فیلم آموزش رایگان

آلبرت انیشتین اولین نظریه‌های خود را در سال ۱۹۰۵ منتشر کرد. او در مقاله اول خود، روشی را جهت اندازه‌گیری ابعاد اتم و مکانیزم حرکت آن‌ها ارائه داد. در مقاله دیگری مفهوم نسبیت خاص خود را معرفی کرد. این نظریه‌ای بود که نهایتا منجر به شهرت جهانی برای او شد. او هم‌چنین یکی از نتایج نسبیت خاص خود را در مقاله‌ پنجمش ارائه داد. نتیجه مذکور عنوان می‌کرد که ماده و انرژی معادل هم هستند؛ در حقیقت ارتباط بین ماده و انرژی را در قالب معروف‌ترین معادله تاریخ فیزیک یعنی E=MC² بیان کرد.

فارغ از تمام نظریه‌های بیان شده در بالا، مقاله‌ای که جایزه نوبل فیزیک را در سال ۱۹۲۱ برای انیشتین به ارمغان آورد، اثری تحت عنوان «اثر فتوالکتریک» را توضیح می‌داد. در این مطلب قصد داریم تا این اثر را به زبان ساده توضیح دهیم. لازم به ذکر است که مفاهیم این اثر، فیزیک و اساس کار فوتوسل‌ها را تشکیل می‌دهد. جهت آشنایی با فوتوسل‌ها به مقاله «فوتوسل -- به زبان ساده» مراجعه فرمایید.

اثر فوتوالکتریک چیست؟

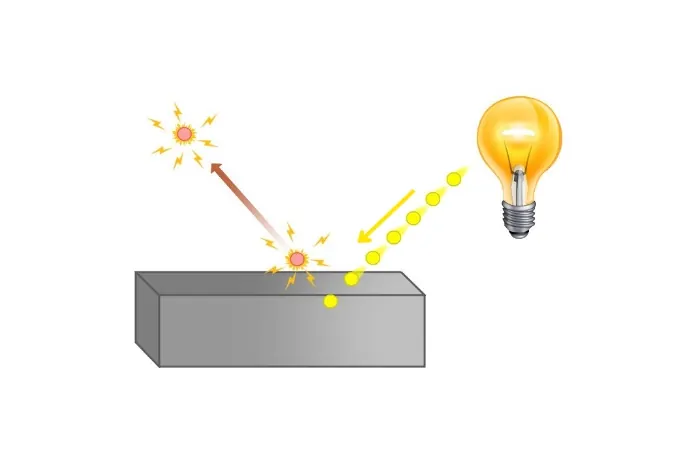
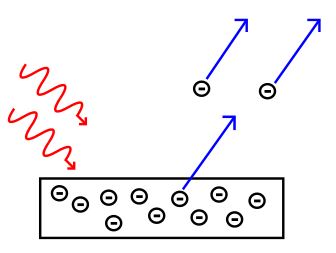
زمانی که نوری با بسامد مناسب روی سطحی فلزی تابیده شود،‌ انرژی الکترون‌ها افزایش یافته و از سطح فلز جدا می‌شوند. به این پدیده، اثر فوتوالکتریک و به الکترون‌هایی که از سطح فلز جدا می‌شوند، فوتوالکترون می‌گویند. فوتوالکترون‌ها از نظر خواص فیزیکی و رفتار، تفاوتی با بقیه الکترون‌ها ندارند. پیشوند فوتو، بر این نکته تاکید می‌کند که جدا شدن الکترون‌ها از سطح در نتیجه تابش نور است. در شکل زیر شماتیک مفهوم بیان شده نشان داده شده است.

فرض موجی بودن نور

در قرن نوزدهم میلادی، فیزیکدانان به‌منظور توضیح اثر فوتوالکتریک، نور را به‌ صورت نواسانات میدان الکتریکی تصور می‌کردند که با تابش روی سطح، الکترون‌ها را داغ کرده و آن‌ها را از سطح جدا می‌کند. این توضیح مبتنی بر این فرض بود که نور فقط یک موج است که در فضای خلاء‌ منتشر می‌شود.

دانشمندان هم‌چنین معتقد بودند که انرژی موج نوری به میزان درخشندگی آن وابسته است. آن‌ها هم‌چنین این‌طور فکر می‌کردند که میزان درخشندگی نور نیز با افزایش دامنه این موج، زیاد می‌شود. در نتیجه به‌منظور اعتبارسنجی این فرضیات، آزمایشاتی را انجام دادند که هدف از انجام آن‌ها اندازه‌گیری تغییرات نرخ الکترون‌های جدا شده و انرژی جنبشی آن‌ها بر حسب فرکانس و دامنه موج ورودی بود.

با توجه به توصیفات کلاسیک ارائه شده از نور تا آن زمان، دانشمندان، انتظار داشتند، آزمایشات نتایج زیر را نشان دهند.

• انرژی جنبشی ذرات الکترون با افزایش دامنه نور ورودی بایستی افزایش یابد.
• تعداد الکترون‌های جدا شده با افزایش فرکانس نور نیز بایستی افزایش یابد.

جهت درک این‌که چرا این دو پیش‌ بینی انجام شد، می‌توان امواج نوری را همانند امواج آب تصور کرد. فرض کنید تعدادی توپ مطابق با شکل زیر روی بستری قرار گرفته‌اند و بستر مذکور نیز در آب قرار دارد. بستر، نماد سطح فلز است و توپ‌ها، الکترون‌ها را نشان می‌دهند. بدیهی است که موج‌های آب، معادل با امواج نوری در نظر گرفته شده‌اند.

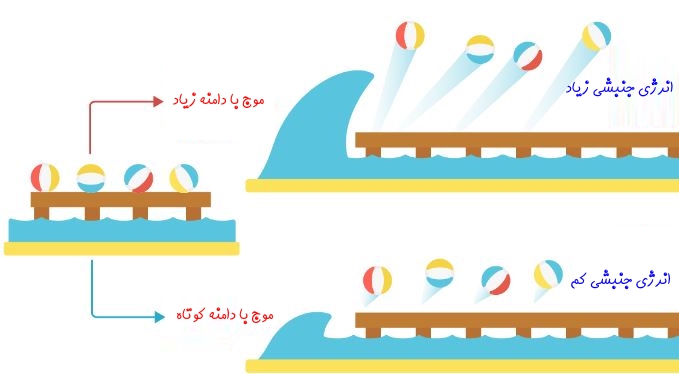
اگر ارتفاع امواج (معادل با دامنه موج نوری) برخوردی به بستر افزایش یابد، توپ‌های قرار گرفته روی آن‌ نیز با انرژی بیشتری جدا خواهند شد. این در حالی است که با افزایش نوسانات جریان، تعداد توپ‌های جدا شده نیز افزایش می‌یابد. از این رو دانشمندان انتظار داشتند که در مقیاس اتم نیز همین اتفاق بیافتد؛ یعنی با افزایش دامنه نور برخوردی به سطح، انرژی الکترون‌های جدا شده بیشتر شود. هم‌چنین با افزایش فرکانس نور ورودی، تعداد الکترون‌های بیشتری جدا شود.

شکست نتایج

پس از انجام آزمایشات، جهت بررسی تاثیر دامنه و فرکانس نور ورودی، نتایج زیر مشاهده شد:

• انرژی جنبشی الکترون‌ها با افزایش فرکانس نور ورودی،‌ افزایش یافتند.
• جریان الکتریکی در نتیجه افزایش فرکانس نور، ثابت ماند.
• جریان الکتریکی در نتیجه افزایش دامنه نور وروی به سطح، زیاد شد.
• انرژی جنبشی فوتوالکترون‌ها در نتیجه افزایش دامنه نوسانات ثابت ماند.

در حقیقت نتایج بالا به کلی عکس پیش‌ بینی‌ها را نشان می‌داد. به‌نظر می‌رسید جهت توضیح آزمایشات انجام شده، نیاز است تا مدل جدیدی انتخاب شود. این مدل توسط آلبرت انیشتین پیشنهاد شد. او نور را به‌صورت ذراتی گسسته از انرژی الکترومغناطیسی فرض کرد که امروزه آن را فوتون می‌نامند.

انرژی یک فوتون را می‌توان با استفاده از قانون پلانک که در زیر آمده محاسبه کرد:

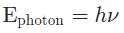
در رابطه بالا E نشان دهنده انرژی یک فوتون است که بر حسب ژول بیان می‌شود. هم‌چنین h را ثابت پلانک می‌نامند و مقدار آن برابر با $$6.626 × 10^{-34} \enspace J.s$$ است. عدد $$\nu$$ نیز نشان دهنده فرکانس نور است. طبق رابطه پلانک، انرژی یک فوتون متناسب با فرکانسش ($$\nu$$) و دامنه آن متناسب با تعداد فوتون‌ها است. توجه داشته باشید فرکانس نور را با نماد f نیز نشان می‌دهند.

فرکانس نور و فرکانس آستانه ($$\nu_0$$)

ما می‌توانیم نور برخوردی به سطح را به صورت جریانی از فوتون‌ها در نظر بگیریم، به نحوی که انرژی آن‌ها متناسب با فرکانس نور برخوردی باشد. هنگامی که یک فوتون به یک سطح فلزی برخورد می‌کند.

فیلم آموزش فیزیک مدرن با رویکرد حل مساله در فرادرس

کلیک کنید

انرژی فوتون توسط الکترون‌های سطح جذب می‌شود. تصویر ارائه شده در پایین، انرژی جنبشی الکترون‌های آزاد شده را بر حسب فرکانس نور ورودی نشان می‌دهد.

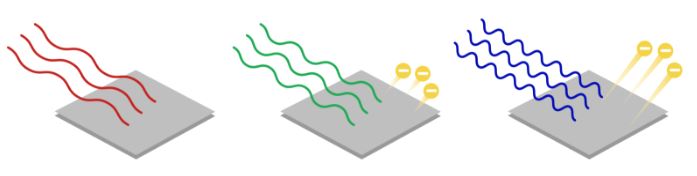
توجه داشته باشید که در تصویر بالا بیشترین فرکانس را نور آبی و کم‌ترین فرکانس را نور قرمز دارد. دانشمندان در آزمایشاتی که انجام دادند، مشاهده کردند که فارغ از دامنه نور ورودی به سطح‌، اگر فرکانس نور از عدد معینی ($$\nu_0$$) کم‌تر باشد، دیگر الکترونی از سطح جدا نخواهد شد. $$\nu_0$$ را فرکانس آستانه می‌نامند.

علاوه بر این، انرژی جنبشی فوتو‌الکترون‌ها متناسب با فرکانس نور است. نمودارهای زیر رابطه بین فرکانس نور برخوردی به سطح و انرژی جنبشی الکترون‌های آزاد شده را نشان می‌دهد.

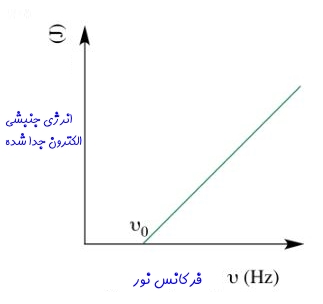
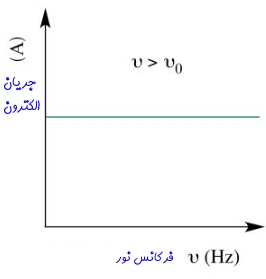
از آنجایی که دامنه نور با افزایش فرکانس آن، ثابت نگه داشته شده، در نتیجه تعداد فوتون‌های جذب شده توسط سطح نیز ثابت می‌ماند. بنابراین نرخ الکترون‌هایی که از سطح جدا می‌شوند نیز ثابت خواهند ماند [این نرخ معادل با جریان الکتریکی است]. در شکل زیر ارتباط بین جریان الکترون‌های جدا شده و فرکانس نور ورودی به سطح نشان داده شده است.

توضیح کمی‌تر اثر فوتوالکتریک

رابطه بین فرکانس ورودی به سطح و انرژی فوتوالکترون‌های جدا شده را می‌توان با استفاده از قانون پایستگی انرژی توضیح داد. در حقیقت انرژی فوتون ورودی (E_photon) برابر با حاصل جمع انرژی جنبشی الکترونِ جدا شده (KE_electron) و انرژی مورد نیاز جهت جداسازی الکترون‌ از سطح است. به انرژی مورد نیاز جهت جداسازی الکترون از سطح یک فلز،‌ «تابع کار سطح» گفته می‌شود. این کمیت را با نماد Φ نشان می‌دهند. بنابراین رابطه زیر بین انرژی ورودی به سطح و انرژی الکترون‌های جدا شده از آن وجود دارد.

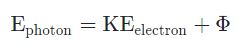
همانند مقدار $$\nu_0$$، مقدار Φ نیز وابسته به نوع فلز است. در نتیجه مقدار انرژی فوتون بر حسب فرکانس نور را می‌توان با استفاده از قانون پلانک،‌ به شکل زیر بیان کرد:

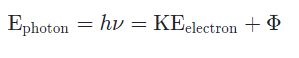
در نتیجه انرژی جنبشی فتوالکترون را می‌توان با استفاده از رابطه زیر بدست آورد:

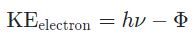
می‌توان دید که برای مقادیر بیشتر از تابع کار، انرژی جنبشی یک فوتوالکترون به‌صورت خطی با افزایش فرکانس نور ورودی ($$\nu$$)، افزایش می‌یابد؛ هم‌چنین با استفاده از رابطه بالا می‌توان سرعت فوتوالکترون جدا شده (v) را بدست آورد. در حقیقت این سرعت با استفاده از رابطه کلاسیک انرژی جنبشی، به‌صورت زیر بدست می‌آید.

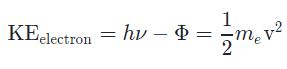
در رابطه بالا m_e، نشان دهنده جرم الکترون ساکن، برابر با $$9.1094×10^{-4} \enspace kg$$ است.

روند دامنه موج وارد شده به سطح

دامنه بالاتر نور، به معنای برخورد بیشتر فوتون‌‌ها به سطح است. در یک بازه زمانی مشخص، دامنه موج بزرگتر منجر به جدا شدن الکترون‌های بیشتر از سطح خواهد شد؛ بنابراین در فرکانس‌های بیشتر از فرکانس آستانه، افزایش دامنه نور منجر به افزایش جریان الکترون‌های جدا شده می‌شود.

در شکل ۱ افزایش جریانِ ناشی از زیاد شدن فرکانس ورودی نشان داده شده. از آنجایی افزایش دامنه نور، انرژی فوتون‌هایش را تغییر نمی‌دهد، در نتیجه انرژی جنبشی فوتوالکترون جدا شده نیز با افزایش دامنه نور ورودی ثابت می‌ماند (شکل ۲). اگرچه حجم بسیاری از مطالب بالا به‌صورت کیفی بیان شده، اما مفاهیم نهفته در آن بسیار مهم هستند. از این رو جهت تسلط بیشتر به موضوع، مطالعه مثال‌های زیر توصیه می‌شوند.

مثال ۱: اثر فوتوالکتریک مس

تابع کار فلز مس برابر با $$\phi=7.53×10^{-19} \enspace J$$ است. فرض کنید نوری را با فرکانس $$3×10^{16} \enspace Hz$$ به سطح مس می‌تابانیم. آیا اثر فوتوالکتریک مشاهده خواهد شد؟

جهت جدا شدن فوتوالکترون، انرژی فوتون‌های برخوردی بایستی بیشتر از تابع کار فلز مس باشند. از این رو در ابتدا انرژی فوتون‌ها را با استفاده از رابطه پلانک، به شکل زیر بدست می‌آوریم.

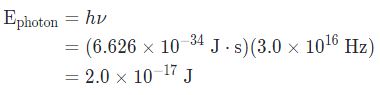
با مقایسه انرژی فوتون بدست آمده با تابع کار فلز مس، متوجه خواهیم شد که انرژی فوتون بیشتر است. در حقیقت:

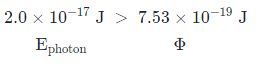
در نتیجه با تابش نور، الکترون جدا خواهد شد و اثر فوتوالکتریک نیز رخ خواهد داد.

مثال ۲: محاسبه انرژی جنبشی فوتوالکترون

انرژی جنبشی فوتوالکترون‌های جدا شده در مثال قبل چقدر هستند؟

همان‌طور که در بالا نیز بیان شد، می‌توان با نوشتن قانون پایستگی انرژی به صورت زیر، انرژی جنبشی الکترون جدا شده را بدست آورد.

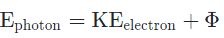
حال با قرار دادن مقادیر تابع کار و انرژی فوتون ورودی از مثال ۱، انرژی فوتوالکترون برابر می‌شود با:

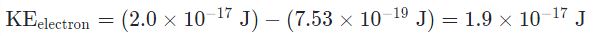
مثال ۳: نور بنفش

فرض کنید نوری بنفش با طول موج ۴۲۰ نانومتر را به سطح کلسیوم می‌تابانیم. با فرض این‌که تابع کار کلسیوم برابر با $$2.71 \enspace eV$$ باشد، موارد زیر مطلوب است:

1.  انرژی این نور بر حسب الکترون-ولت چقدر است؟
2. بیشترین انرژی فوتوالکترون‌های جدا شده از سطح را محاسبه کنید.

(I): در بالا گفتیم که انرژی فوتون،‌ با استفاده از قانون پلانک،‌ به شکل زیر توصیف می‌شود.

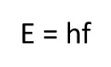
از طرفی رابطه بین طول موج و فرکانس یک موج به‌شکل زیر است.

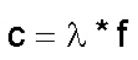
با جایگذاری رابطه بالا در قانون پلانک، داریم:

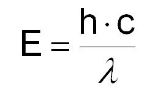
در نتیجه انرژی فوتون‌های نور بنفش برابر است با:

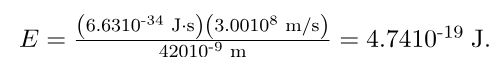
توجه داشته باشید که با کوچک بودن انرژی فوتون و الکترون از واحد الکترون-ولت استفاده می‌شود. در حقیقت ۱ الکترون-ولت برابر با $$1.61×10^{-19} \enspace J$$ است.

(II): با بدست آمدن انرژی فوتون ورودی و با داشتن تابع کار کلسیوم، انرژی فوتوالکترون جدا شده برابر است با:

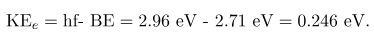
نتیجه‌گیری

فتوالکتریک پدیده‌ای بسیار مهم در علم فیزیک است که در بسیاری از کاربردها از جمله موارد زیر استفاده می‌شود:

• تکنولوژی تصویربرداری
• مطالعه فرآیند‌های هسته‌ای
• مطالعه خواص شیمیایی سطوح
• استخراج اطلاعات تئوری در مورد این‌که رفتار الکترون‌ها در شرایط مختلف به چه شکل است.

علاوه بر کاربرد‌های اشاره شده در بالا، به جرأت می‌توان گفت که مهم‌ترین نتیجه اثر فوتوالکتریک، ایجاد مفاهیم مکانیک کوانتومی است. بنابراین این اثر زمینه‌سازی علمی را فراهم آورده که می‌توان با استفاده از آن کامپیوتر‌هایی ساخت که سرعت بسیار زیادی را به نسبت کامپیوتر‌های امروزی دارند. برای نمونه گوگل پروژه‌ای را آغاز کرده که هدف آن ساخت پردازشگری با سرعت ۱۰۰۰۰۰۰۰۰ برابرِ سرعت کامپیوتر‌های معمولی است!

در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک آموزش‌های زیر به شما پیشنهاد می‌شود:

• مجموعه آموزش‌های دروس فیزیک
• مجموعه آموزش‌های ریاضی و فیزیک
• آموزش فیزیک پایه ۱
• اصول انتقال حرارت — بخش سوم: تابش
• آموزش مکانیک کوانتومی ۱