عدم قطعیت هایزنبرگ — به زبان ساده

در مطالب گذشته وبلاگ فرادرس در مورد برخی از مفاهیم فیزیک مدرن هم‌چون فضا-زمان، فوتون و اتساع زمان صحبت شد. در همین راستا در این مطلب قصد داریم تا یکی از اجزاء جذاب مکانیک کوانتومی تحت عنوان اصل عدم قطعیت هایزنبرگ را توضیح دهیم.

مقدمه

اصل عدم قطعیت هایزنبرگ یکی از نتایج مهم مکانیک کوانتومی است که بیان می‌کند نمی‌توان به طور همزمان همه‌ کمیت‌های یک الکترون را اندازه‌گیری کرد. در حقیقت شما نمی‌توانید به طور همزمان و به شکلی دقیق، موقعیت و تکانه یک الکترون را اندازه‌گیری کنید. این اصل بیان می‌کند که رابطه‌ای بنیادی میان اندازه‌گیری کمیت‌های یک الکترون وجود دارد. برای نمونه هرچه دقت اندازه‌گیری در موقعیت یک ذره بیشتر باشد، دقت اندازه‌گیریِ تکانه یا مومنتوم کمتر خواهد بود. عدم قطعیت هایزنبرگ مفهومی را بیان می‌کند که مکانیک نیوتونی قادر به توجیه آن نیست.

فیلم آموزش فیزیک مدرن با رویکرد حل مساله در فرادرس

کلیک کنید

اصل عدم قطعیت هایزنبرگ، مفهومی است که بیان می‌کند چرا یک فیزیکدان نمی‌تواند به طور دقیق، کمیت‌های مرتبط با یک الکترون را اندازه‌گیری کند. تا قبل از ارائه کوانتوم مکانیک، تصور بر این بوده که تمامی ویژگی‌های یک جسم در لحظه را می‌توان با دقت قابل قبولی اندازه‌گیری کرد.

فیزیک نیوتونی حدی را برای دقت در اندازه‌گیری کمیت‌های فیزیکی یک جسم در نظر نمی‌گیرد. این در حالی است که هایزنبرگ معتقد بود مشخصه‌های یک ذره را می‌توان تا حد مشخصی از دقت اندازه‌گیری کرد. این حد باعث می‌شود همواره اطلاعات ما در مورد یک ذره در حد مشخصی باقی بماند. برای نمونه اگر شخصی مکان یک ذره را با دقت بالایی اندازه‌ بگیرد، قطعا سرعت آن در فرآیند اندازه‌گیری تحت تاثیر قرار گرفته و دقت اندازه‌گیری آن پایین خواهد آمد. این قانون را می‌توان در مورد انرژی و زمان نیز عنوان کرد. در حقیقت اگر بخواهیم به طور کمی‌تر بیان کنیم، می‌توان گفت بیشترین دقت اندازه گیری تکانه و موقعیت الکترون مطابق با نامساوی زیر توصیف می‌شود.

$$ \large \Delta { p } \Delta { x } \ge \dfrac { h } { 4 \pi } $$

رابطه فوق را می‌توان بین انرژی و زمان برای الکترون نیز به صورت زیر بیان کرد:

$$ \large \Delta { t } \Delta { E } \ge \dfrac { h } { 4 \pi } $$

در رابطه فوق $$ Δ $$ نشان دهنده خطا در اندازه‌گیری و $$h$$، ثابت پلانک را نشان می‌دهد. بدیهی است که در رابطه فوق هر چه یکی از ترم‌های ضرب شده در یکدیگر کوچک‌تر باشند، ترم دوم نیز بزرگ‌تر خواهد بود.

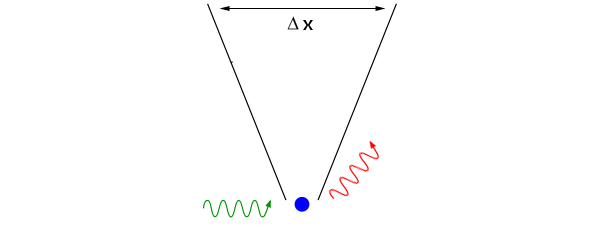
به عنوان مثال فرض کنید هدف، اندازه‌گیری مومنتوم یک توپ تنیس و یک الکترون است. برای این اندازه‌گیری به نور نیاز است. در چنین آزمایشی فرض بر این است که نور از فوتون تشکیل شده است. هنگامی که فوتون به هریک از این ذرات برخورد کند، مومنتومی میان آن‌ها منتقل خواهد شد. توجه داشته باشید که مومنتوم یک ذره با سرعت $$v$$ و جرم $$m$$ مطابق با رابطه زیر بدست خواهد آمد.

$$\large p = m v $$

هنگامی که الکترون به فوتون برخورد می‌کند، کسری از مومنتوم آن به الکترون منتقل می‌شود. اندازه این کسر وابسته به نسبت جرم الکترون و فوتون است. همین‌ رخ‌داد را می‌توان در مورد انتقال مومنتوم از فوتون به توپ تنیس نیز بیان کرد. اما در این حالت میزان مومنتوم اندازه‌گیری شده، دقت کمتری دارد. دلیل این امر نیز این است که جرم توپ تنیس چندین برابر جرم فوتون است.

به منظور توصیف دقیق‌تر فرض کنید یک دوچرخه و یک تانک با هم برخورد می‌کنند. در این فرض تانک نقش توپ تنیس و دوچرخه نقش فوتون را بازی می‌کنند. علیرغم اندک بودن سرعت تانک در مقابل سرعت دوچرخه، این برخورد، مومنتوم دوچرخه را به اندازه‌ای بسیار افزایش می‌دهد. به همین صورت این برخورد مومنتوم تانک را زیاد تغییر نمی‌دهد. بنابراین اندازه‌گیری مومنتوم تغییر یافته تانک، بسیار مشکل خواهد بود.

مفهوم عدم قطعیت هایزنبرگ

درک ناتوانی در اندازه‌گیری موقعیت دقیق یک الکترون مشکل به نظر می‌رسد. در نگاه اول این دیدگاه وجود دارد که برای هر نقطه در فضا می‌توان برداری ترسیم کرده و مولفه‌های آن را تعیین کرد. این در حالی است که اصل عدم قطعیت هایزنبرگ دقیقا نقطه مقابل این دیدگاه را نشان می‌دهد. دلیل این امر ماهیت موجی ذرات است. در حقیقت یک ذره در تمامی فضا پخش شده و نمی‌توان یک نقطه مشخص را به موقعیت آن نسبت داد.

فیلم آموزش مکانیک کوانتومی ۱ در فرادرس

کلیک کنید

همین استدلال را می‌توان در مورد تکانه نیز به این صورت بیان کرد که یک ذره، بسته‌هایی از موج را با خود حمل می‌کند که هریک از این بسته‌ها مومنتوم خاص خود را دارند. از این رو در بهترین حالت می‌توان گفت که یک ذره دارای مومنتوم در یک طیف خاص است. در شکل زیر یک بسته موجی نشان داده شده است.

حال حالتی را در نظر بگیرید که در آن مشخصه‌ای کوانتومی به طور دقیق قابل اندازه‌گیری است. بنابراین یک موج که محل دقیق آن قابل اندازه‌گیری است در یک نقطه با طول‌موج‌ها و در نتیجه مومنتوم‌هایی نامشخص پخش شده‌اند. از طرفی یک موج با مومنتوم قابل اندازه‌گیری، طول موجی دارد که به اندازه بینهایت در فضا نوسان می‌کند، بنابراین نمی‌توان محل دقیق آن را به درستی تعیین کرد.

دقیقا آزمایش ذهنی انجام شده در بالا را می‌توان برای انرژی و زمان نیز انجام داد. به منظور اندازه‌گیری دقیق میزان انرژی یک موج، زمانی برابر با بینهایت نیاز است.

نتایج

اصل عدم قطعیت هایزنبرگ تاثیری شگرف در طراحی آزمایش‌های کوانتومی و فیزیک تجربی دارد. به منظور اندازه‌گیری مومنتوم یا موقعیت یک ذره، باید کنشی با آن انجام شود. این کنش منجر به تغییر دیگر مشخصه ذره خواهد شد. برای نمونه به منظور اندازه‌گیری موقعیت یک الکترون باید برخوردی بین آن و ذره دیگری هم‌چون الکترون انجام شود.

با فرض این‌که هدف اندازه‌گیری مومنتوم الکترون باشد، این برخورد مومنتوم را تغییر داده، بنابراین نمی‌توان به مقدار دقیق آن دست یافت. اندازه‌گیری دقیق‌تری از موقعیت الکترون را می‌توان با استفاده ذراتی با طول موج کوتاه‌تر انجام داد. چنین ذراتی دارای فرکانسی بالاتر بوده در نتیجه انرژی آن‌ها نیز بیشتر است. در نتیجه این ذرات با برخوردشان، مومنتوم الکترون‌ها را نسبت ذرات با فرکانس پایین‌تر بیشتر تغییر خواهند داد.

مثال‌ها

در ادامه دو مثال ذکر شده که به منظور درک بهتر ابعاد کمی عدم قطعیت هایزنبرگ، مطالعه آن‌ها خالی از لطف نخواهد بود.

مثال ۱ عدم قطعیت هایزنبرگ

عدم قطعیتِ $$ \Delta { p } $$ (مومنتوم)، در هنگام پرتاب توپ فوتبالی با سرعت $$ 4 0 \; m / s $$، $$\ 1 \times 10 ^ { - 6 } $$ برابر مومنتومِ توپ است. با فرض این که جرم توپ برابر با $$ 0.4 \ kg $$ باشد، عدم قطعیت در اندازه‌گیری موقعیت آن چقدر است؟

به منظور یافتن عدم قطعیت اندازه‌گیری موقعیت مکانی، کافی است از فرمول هایزنبرگ استفاده کنیم. در ادامه این کار انجام شده است.

$$ \large \begin {align} p &=m v \nonumber \\[5pt] &= (0.40\, kg)(40\,m/s) \nonumber \\[5pt] &= 16\,\dfrac{kg \, m} { s } \nonumber \end{align} \nonumber $$

$$ \large \begin{align} \Delta { p } &= p (1 \times 10^{-6})\nonumber \\[5pt] &=16\dfrac { k g \, m } { s } (1 \times 10 ^ { - 6 } ) \nonumber \\[5pt] &=16 \times 10^{-6}\dfrac {k g \, m } { s } \nonumber \end{align} \nonumber $$

$$ \large \begin{align} \Delta{p } \Delta { x } & \ge \dfrac { h } { 4 \pi } \nonumber \\[5pt] \Delta { x } &\ge \dfrac{ h }{ 4 \pi\Delta { p } } \nonumber \\[5pt] &\ge \dfrac{6.626 \times 10^{-34}J \,s} { 4\pi \left ( 16 \times 10^{-6}\dfrac{kg \, m}{s}\right) } \nonumber \\[5pt] &\ge 3.3 \times 10^{-30}m\nonumber \end{align} \nonumber $$

توجه داشته باشید که ۱ ژول معادل با مقدار زیر است.

$$ \large 1 \, J = 1 \dfrac { k g \ m^ 2 } { s^2 } $$

مثال ۲ عدم قطعیت هایزنبرگ

فرض کنید در مثال قبل $$ 2 mL $$ آب روی توپ وجود دارد که برابر با سرعت بیان شده در مثال اول روی توپ در حال حرکت است. خطای اندازه‌گیری $$ \Delta x $$ را محاسبه کنید.

فیلم آموزش اپتیک کوانتومی در فرادرس

کلیک کنید

مقدار حجم به خودی خود دارای اهمیت نیست؛ از این رو در ابتدا باید مقدار حجم آب را به جرم تبدیل کرده و در مرحله بعد از رابطه عدم قطعیت استفاده کرد. با انجام این کار داریم:

$$\large \begin {align*} ( 2 \, mL ) \underbrace{\left(\dfrac{1\,g}{1\,mL}\right)}_{\text{density of water}} \left(\dfrac{1\,kg}{1,000\,g}\right) =2 \times 10^{-3} kg \nonumber \end {align*} $$

$$ \large \begin{align} p & = m v\nonumber \\[5pt] &= (2 \times 10^{-3} kg)(40\,m / s ) \nonumber \\[5pt] &= 8 \times 10^ { - 2 } \dfrac{kg \, m}{s}\nonumber \end {align} \nonumber$$

$$ \large \begin{align} \Delta { p } &=p (1 \times 10^{-6}) = (8 \times 10^{-2} \dfrac{kg \, m} {s } ) ( 1 \times 10^{-6}) \\ & = 8 \times 10^ { - 8 } \dfrac{kg \, m}{s} \nonumber \end {align} \nonumber $$

$$\large \begin{align} \Delta { p } \Delta{x} &\ge \dfrac{h}{4\pi} \\ \Delta { x } &\ge \dfrac { h } { 4 \pi\Delta { p } } \nonumber \\[5pt] &\ge \dfrac { 6.626 \times 10^{-34} J \, s } { 4 \pi \left ( 8 \times 10^{-8} \dfrac{kg \, m }{s}\right)}\nonumber \\[5pt] & \ge 6.6 \times 10 ^ {-28} m \nonumber \end{align} \nonumber $$

$$ \large \begin{align} p&=m v \nonumber \\[5pt]&= (9.1 \times 10^{-31} k g ) ( 40\,m/s) \nonumber \\[5pt] &= 3.6 \times 10 ^ { -29 }\dfrac { k g \, m } { s } \nonumber \end{align} \nonumber$$

$$ \large \begin{align} \Delta { p } &= p \times 10^{-6} \nonumber \\[5pt] &= 3.6 \times 10 ^ { -29 } \dfrac { k g \, m}{s} \times 1 \times 10 ^ { -6} \nonumber \\[5pt] &= 3.6 \times 10^{-35} \dfrac { k g \, m } { s } \nonumber \end{align} \nonumber $$

$$ \large \begin{align} \Delta { p } \Delta { x } &\ge \dfrac { h } { 4\pi } \nonumber \\[5pt] \Delta { x } & \ge \dfrac{h}{4\pi\Delta{p}} \nonumber \\[5pt] & \ge \dfrac{6.626 \times 10 ^ { - 34 } J \times s}{4\pi 3.6 \times 10 ^ {-35} \dfrac{kg \, m } { s } } \nonumber \\[5pt] &\ge1.5\,m \nonumber \end{align} \nonumber $$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مدل اتمی بور — به زبان ساده
• اوربیتال و آرایش الکترونی — به زبان ساده
• طیف اتمی — از صفر تا صد

^^