فرکانس — به زبان ساده

اگر تا به امروز مفهوم فرکانس برایتان سوال است، یا درک شهودی مناسبی از آن ندارید، در این مقاله از مجله فرادرس در نظر داریم تا با زبانی ساده به تعریف و مفهوم فرکانس (Frequency) یا معادل فارسی آن، بسامد بپردازیم.
تعریف فرکانس
به طور خلاصه، فرکانس را میتوان تعداد تکرار یک واقعه در واحد زمان تعریف کرد. این تعریف که به فرکانسِ زمانی نیز موسوم است، به تقابل دو فرکانسِ زاویهای و فرکانسِ فضایی تاکید دارد. در ادامه به معرفی دو فرکانسِ زاویهای و فضایی نیز خواهیم پرداخت.
با توجه به مطلب فوق، میتوانیم مفهومی دیگر از تعریف فرکانس را موسم به دوره (Period) استخراج کنیم. دوره که اصولاً با نام دوره تناوب شناخته میشود، مدت زمانی است که یک رخداد یا واقعه، روند یا سیکل (Cycle) کاملی را (۱ بار) طی میکند. در واقع دوره تناوب را میتوانیم عکس فرکانس تعریف کنیم. در فیزیک و علوم مهندسی، فرکانس را با نماد یا و دوره تناوب را با نماد نمایش میدهند.
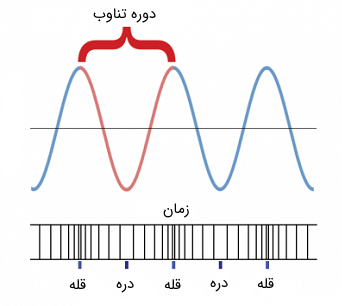
بدیهی است که واحد دوره تناوب در سیستم استاندارد ، ثانیه است. واحد فرکانس را به افتخار فیزیکدان آلمانی «هاینریش رودلف هرتز» (Heinrich Rudolf Hertz)، هرتز مینامند و با نماد نمایش میدهند ().

به عنوان مثال اگر، قلب یک نوزاد تازه متولد شده با فرکانسِ 120 بار در دقیقه تپش کند، دوره تناوب عمل تپش، یعنی مدت زمانی که ۱ عمل کامل تپش (انقباض و انباسط قلب) رخ میدهد 0.5 ثانیه است (60 تقسیم بر 120). میزان نرخ نوسازی تصویر یا «رفرشرِیت» (Refresh Rate) که بر حسب فرکانس بیان میشود، مثالی دیگر از واحد فرکانس است. به طور مثال مانیتوری با رفرشریت ، در ۱ ثانیه تصویرش 120 بار تکرار میشود.

جهت درک بهتر این امر به تصویر متحرک زیر دقت کنید. تصویر زیر که کاملاً گویای رابطه () است، بیان میکند که هرچه مدت زمان رخ دادن واقعهای که به طور پیوسته تکرار میشود (در اینجا چشمک زدن دایرهها) کمتر باشد، فرکانسِ آن بیشتر است.
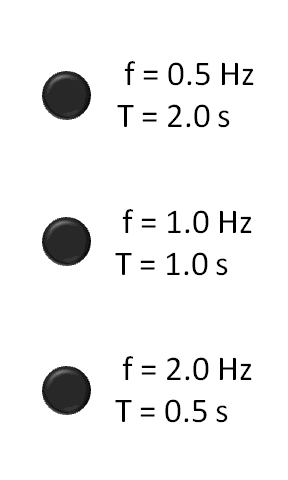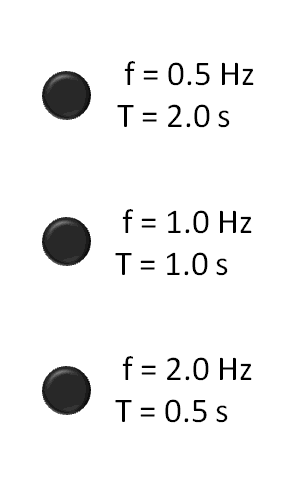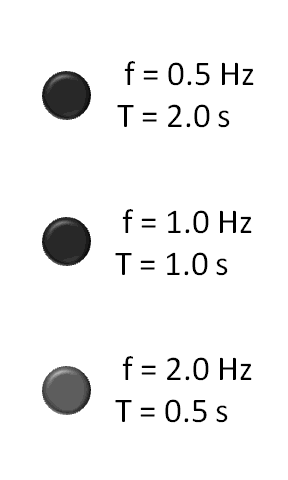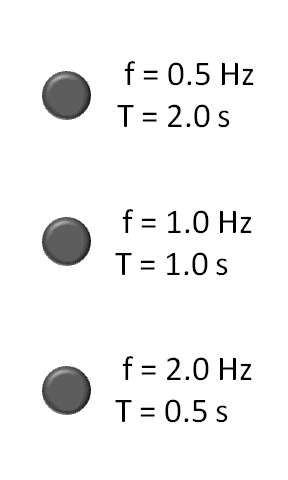
در سیستمهای مکانیکی دوار نیز که با واحد rpm (دور بر دقیقه) سنجیده میشوند، به هر 60 دور در دقیقه، 1 هرتز میگویند ().
فرکانس یکی از مهمترین پارامترهای فیزیک و علوم مهندسی است که به وسیله آن، تمامی پدیدههای ارتعاشی، نوسانی و انواع موجهای مکانیکی و صوتی را تفسیر میکنند. از آنجا که دوره تناوب و فرکانس در واقع یک مفهوم هستند، جهت راحتی کار، معمولاً برای امواج آهسته و طولانی نظیر امواج سطحی اقیانوسها از دوره تناوب موج و برای امواج کوتاه و سریع از فرکانس استفاده میکنند. در جدول زیر دوره تناوب نظیر هر فرکانس آمده است:
| فرکانس (هرتز) | ||||||
| دوره تناوب (ثانیه) |
فرکانس زاویه ای (Angular Frequency)
فرکانسِ زاویهای که با نماد یونانی «اُمگا» (Omega : ω) نمایش داده میشود، پارامتری است که میزان یا نرخ تغییر (جابهجایی) زاویهای بر حسب رادیان را در سیستمهای دوار (چرخشی) توصیف میکند. همچنین در امواج متناوب سینوسی شکل (sinusoidal) میزان تغییر فاز را مشخص میکند.
فرکانسِ زاویهای با واحد رادیان بر ثانیه () نمایش داده میشوند. فرکانسِ زاویهای به میزان از فرکانسِ عادی بزرگتر است.
فرکانس فضایی یا مکانی (Spatial Frequency)
فرکانسِ فضایی همانند فرکانس زمانی تعریف میشود. با این تفاوت که محور زمانی با محور مکانی (یک یا چند بعدی) جایگزین میشود. به طور مثال:
عدد که به عدد موج معروف است، همان فرکانسِ فضایی بوده که با واحد رادیان بر متر اندازهگیری میشود. در حالتهای دو و سه بعدی، عدد موج فرم برداری، موسوم به بردار موج، به خود میگیرد:
در شکل زیر میتوانید رابطه ساده ریاضی بین پارامترهایی که در فوق معرفی کردهایم را مشاهده کنید.
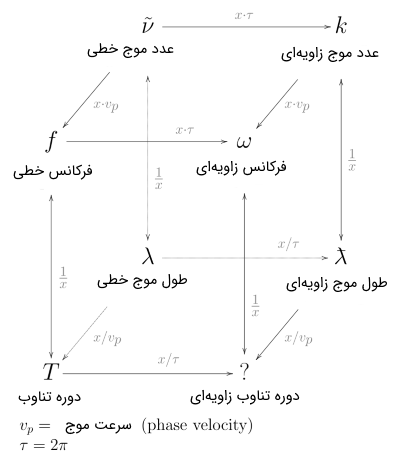
انتشار موج
در محیطهای معمولی و عادی، یعنی محیطهایی که سرعت انتقال موج مستقل از فرکانس است، فرکانس با معکوس طول موج ارتباط دارد. ضریب تناسب بین فرکانس و طول موج، سرعت انتشار موج است. پس حتی در محیطهای پاشنده نیز، فرکانسِ موج با سرعت فاز () موج در آن محیط و طول موج به فرم زیر وابسته است:
میدانیم که امواج الکترومغناطیسی در خلأ با سرعت نور () حرکت میکنند، پس رابطه فوق به شکل زیر تغییر میکند که در آن سرعت نور در خلأ است.
توجه داشته باشید هنگامی که موج الکترومغناطیسی تولید شده از یک منبع تک رنگ (تک فرکانس) که از یک محیط به محیط دیگر میرود، فرکانس آن ثابت مانده و فقط سرعت و طول موج آن طبق رابطه تغییر میکنند. جهت آشنایی با پارامتر طول موج، به مقاله «طول موج -- به زبان ساده» مراجعه فرمایید.

اندازهگیری فرکانس
سادهترین راه جهت محاسبه فرکانس یک واقعه، نظیر نوسان یک آونگ، چرخش یک دیسک، یا تکرار قلههای یک موج و ... شمارش تعداد تکرار واقعه در یک بازه زمانی خاص است. با تقسیم تعداد تکرار آن واقعه به بازه زمانی، فرکانس به دست میآید. به طور مثال اگر یک واقعه به تعداد 71 مرتبه در مدت زمان 15 ثانیه تکرار شود، فرکانس این واقعه به صورت زیر محاسبه میشود:
شمارنده فرکانس (Frequency Counter) یا اسیلوسکوپ (Oscilloscope)

امروزه جهت محاسبه فرکانس سیگنالهای الکتریکی در فیزیک و مهندسی برق از ابزاری الکترونیکی موسوم به شمارنده فرکانس (Frequency Counter) استفاده میکنند. این ابزار به صورت خودکار فرکانس سیگنال ورودی را محاسبه و در واحد هرتز () نمایش میدهد. این کار توسط اسیلوسکوپها (Oscilloscope) نیز قابل انجام است. در واقع میتوان گفت که اسیلوسکوپ درون خود یک شمارنده فرکانس نیز جای داده است.

جهت محاسبه فرکانسِ فرآیندهای مکانیکی نظیر چرخش، نوسانات و لرزشها و ... میتوان آنها را با مبدلهایی به سیگنالهای الکتریکی معادل تبدیل و سپس توسط شمارندههای فرکانس، اقدام به محاسبه فرکانسِ آنها کرد. امروزه دستگاههای مذکور توانایی محاسبه فرکانس تا حد 100 گیگاهرتز را دارند. جهت محاسبه فرکانسهایی بیشتر از این مقدار، از روشهای غیرمستقیم استفاده کرد.
روش هتروداین (Heterodyne Method)
یکی از روشهای کاربردی جهت محاسبه فرکانسِ امواج الکترومغناطیسی که فرکانسی بیشتر از حد توان محاسبه دستگاههای شمارنده فرکانس دارند، روش محاسبه غیر مستقیم، موسوم به هترودینگ (Heterodyning) یا تبدیل فرکانسی است.
در این روش یک سیگنال (موج) مرجع با فرکانسی معلوم که در نزدیکی فرکانس نامعلوم موج مذکور است را با سیگنال مجهول در دستگاهی غیرخطی نظیر دیود، مخلوط (Nonlinear Mixing Device) میکنیم. این کار باعث ایجاد یک پالس/بیت (Beat) یا هتروداین (Heterodyne) در اختلاف فرکانسی دو موج میشود. به شکل زیر دقت کنید.
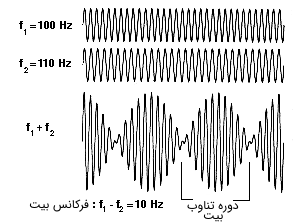
با ادامه این کار میتوانیم نزدیکترین فرکانس به فرکانس موج مجهول را پیدا کنیم. امروزه سعی در استفاده از این روش، جهت تشخیص فرکانسهای بالا (ناحیه اپتیکی) دارند که به تشخیص هتروداین نوری (Optical Heterodyne Detection) معروف است.
مثالهایی از فرکانسهای مختلف
در این بخش در نظر داریم تا با فرکانس آشناترین موردهایی که در زندگی روزمره با آنها در تعامل هستیم، آشنا شویم.
امواج الکترومغناطیسی
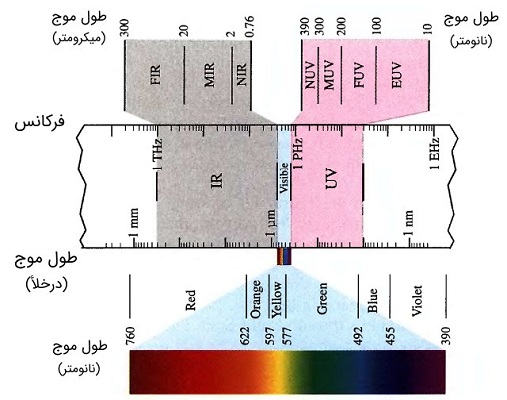
در مقاله «طیف الکترومغناطیسی -- به زبان ساده» به طور جامع با طیف الکترومغناطیسی آشنا شدیم. دیدیم که این امواج الکترومغناطیسی که از میدانهای الکتریکی و میدانهای مغناطیسی عمود بر هم تشکیل شدهاند، از فرکانسهای کم به فرکانسهای زیاد گسترش مییابند. هر ناحیه فرکانسی در این طیف بر حسب کاربرد و رفتار موج در آن ناحیه، نام متفاتی دارند. در شکل زیر طیف الکترومغناطیسی در ناحیههای مختلف نشان داده شده است.
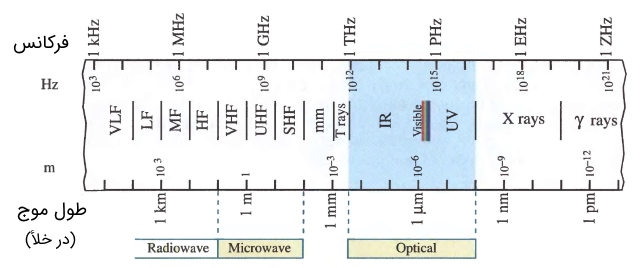
مهندسان برق مخابرات که عموماً با فرکانسهای رادیویی (Radio waves) و میکروویو (Microwave) سروکار دارند، جهت راحتی کار و تدوین استانداردهای مربوطه به حوزه کاری خود، همانطور که در شکل (10) نیز مشخص است، فرکانسهای مختلف را به شرح زیر نامگذاری (طبقهبندی یا ناحیهبندی) میکنند. به طور مثال فرکانسهای VHF به بالا، کاربرد بسیار زیادی در سیستمهای راداری دارند.
| شماره باند | بازه فرکانسی | نام بازه فرکانسی | مخفف بازه | نام انگلیسی |
| 1 | 3~30 Hz | فرکانسهای فوق پایین | ELF | Extremely Low Frequencies |
| 2 | 300~3000 Hz | فرکانس صدا | VF | Vioce Frequencies |
| 3 | 3~30 KHz | فرکانسهای بسیار پایین | VLf | Very Low Frequencies |
| 4 | 30~300 KHz | فرکانسهای پایین | LF | Low Frequencies |
| 5 | 300~3000 KHz | فرکانسهای متوسط | MF | Medium Frequencies |
| 6 | 3~30 MHz | فرکانسهای بالا | HF | High Frequencies |
| 7 | 30~300 MHz | فرکانسهای بسیار بالا | VHF | Very High Frequencies |
| 8 | 300~3000 MHz | فرکانسهای ماورای بالا | UHF | Ultra High Frequencies |
| 9 | 3~30 GHz | فرکانسهای فوقالعاده زیاد | SHF | Super High Frequencies |
| 10 | 30~300 GHz | فرکانسهای به شدت بالا | EHF | Extremely High Frequencies |
| 11 | 300GHz ~ 3THz | تراهرتز | THF | Tremendously High Frequencies |
در حوزه مخابرات فیبر نوری، از آنجایی که مقدار عددی فرکانس بسیار بالا است، جهت راحتی کار، معمولا از طول موج به جای فرکانس استفاده میشود. در طراحی فیبرهای نوری نیز معمولا از واژه طول موج کاری یاد میشود. یادآور میشویم که رابطه بین فرکانس و طول موج به صورت است. نیز سرعت نور در محیط است که بسته به ضریب شکست محیط میتواند متفاوت باشد (). فرکانسهای ناحیه اپتیکی، شامل مادون قرمز، مرئی و فرابنفش نیز در شکل زیر نشان داده شدهاند.
امواج صوتی
در مقاله «شدت صوت -- به زبان ساده» با چگونگی تشکیل امواج مکانیکی صوتی آشنا شدیم. همانند امواج الکترومغناطیسی، امواج صوتی نیز در بازههای فرکانسی خاصی ناحیهبندی شدهاند. این نواحی در شکل زیر نشان داده است:
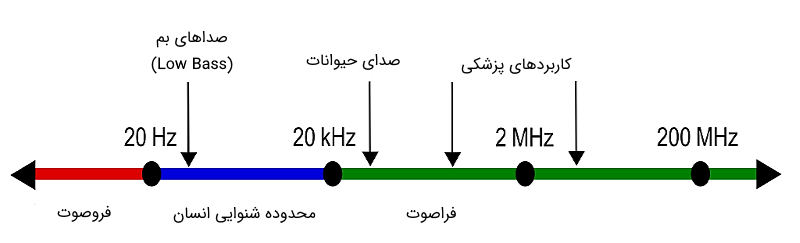
آشناترین بازهای که هر روز به آن سروکار داریم، محدوده شنوایی (آکوستیک) است که از فرکانسهای تا گسترش یافته است. فرکانسهای کمتر از به امواج فروصوت (Infrasound) و امواجی با فرکانسهای بیشتر از به امواج فراصوت (Ultrasound) مشهور هستند.
در بسیاری از محیطهای انتشار، نظیر هوا، سرعت انتقال صوت مستقل از فرکانسِ موج است. بنابراین طول موج امواج صوتی تقریبا معکوس فرکانسِ موج است ().
خطوط جریان
جریان الکتریکی که از طریق خطوط انتقال به سمت کاربران منتقل میشود، از نوع متناوب است. در اکثر مناطق جغرافیایی فرکانس برق شهر به صورت استانداردی جهانی است. در آمریکای شمالی نیز فرکانس برق شهر (جریان متناوب) است. در تصویر زیر، سیگنال جریان متناوبی با دوره تناوب 0.02 ثانیه نشان داده شده است. مطابق با رابطه () فرکانسِ این جریان AC برابر با میشود.

اگر این مطلب از مجله فرادرس برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای فیزیک
- آموزش فیزیک پایه ۲
- مجموعه آموزشهای دروس مهندسی برق
- آموزش الکترومغناطیس مهندسی
- مخابرات نوری -- از صفر تا صد
- امپدانس و محاسبه آن — به زبان ساده
- دی الکتریک — به زبان ساده
^^













سلام استاد عزیز
سوالی درمورد فرکانس داشتم
ایا با تغییر میزان ولوم صدا وکم زیاد کردن ان
فرکانس موزیک عوض میشود
یا تغییر بیس و تریبل پخش تاثیری روی فرکانس
دارد؟
آستانه شنوایی انسان از 20HZ الی 2KHZ میباشد
لطفا این مسئله را حل بفرمایید:
سرعت بارگذاری ۲/۵ میلیمتر بر ثانیه و دامنه جابجایی ۷۵ میلیمتر است. فرکانس بارگذاری چند هرتز است؟
Frequency (Hz) = Speed (mm/s) / Displacement (mm)
Frequency (Hz) = 2.5 mm/s / 75 mm = 0.0333 Hz
باسلام و درود فراوان
آیا کسی میدونه داخل چاه فرکانسی که از فانکشن ژنراتور توسط دوتا میله نازک برنجی خارج میشه به هدف مورد نظر میرسه یا نه اینکه اصلا فشار یا جاذبه زمین داخل چاه این اجازه رو نمیده که فرکانس خروجی بره و به هدف برسه؟
تو بحث امواج الکتریکی هر چی ارتفاع موج بیشتر میشه یعنی ولتاژ افزایش پیدا می کنه
تو بحث الکترومغناطیس این افزایش ارتفاع چه تفسیری میتونه داشته باشه ؟!
سلام وقت بخیر ، ببخشید من میخام فرکانس طبیعی ی نوع سنگ رو ب دست بیاورم ، چه راهی یا فرمولی بایستی انجام بدهم ، لطفت راهنمایی کنید
سلام واحد فرکانس میتونه رادیان بر ثانیه باشه اگه میتونه علتش رو میگید؟
بله، واحد فرکانس نیز می تواند رادیان بر ثانیه (rad/s) باشد. دلیل این امر این است که فرکانس اندازه گیری تعداد چرخه یا نوسان در واحد زمان است. در مورد نوسانات سینوسی، مانند بسیاری از سیستم های مکانیکی، یک سیکل کامل با 2π رادیان مطابقت دارد.
بنابراین، اگر یک فرکانس بر حسب هرتز (Hz) دارید، می توانید با استفاده از رابطه زیر آن را به رادیان در ثانیه (rad/s) تبدیل کنید:
فرکانس (Hz) = فرکانس زاویه ای (rad/s) / (2π)
برعکس، برای تبدیل از راد/ثانیه به هرتز:
فرکانس زاویه ای (rad/s) = فرکانس (Hz) * 2π
این تبدیل به ویژه در هنگام برخورد با سیستم هایی که با توابع مثلثاتی توصیف شده اند مفید است، زیرا به شما امکان می دهد فرکانس را بر حسب رادیان در ثانیه بیان کنید.
صدای ضبط شده روی صفحه گردان با سرعت 45 دور در دقیقه فرکانس 1.23 کیلوهرتز دارد. اگر توسط یک صفحه گردان با سرعت 33.3 دور در دقیقه تکثیر شود چه فرکانسی خواهد داشت؟
فرکانس سنگ چقدره؟
فرکانس الماس چقدره؟
فرکانس طلا چقدره؟
سلام و ادب…سوال بسیار حساسی دارم که در صورت پاسخگویی شما،بینهایت در محاسبات صحیح ترانسهام میتونه نقش مفیدی رو ایفا کنه،لیکن ممنون میشم بنده رو راهنمایی بفرمایید…من تحصیلات عالیه ندارم،به همین دلیل ناچار هستم سوالم رو به شکل کلی تر و ساده تری بیان کنم….سوال اینکه،طبق جدول و بخشنامه ی استاندارد سیمهای روکش دار(در این مورد تاکید بر سیم های لاکی میباشد)چگالی جریان برای مثال،سیم با سطح مقطع ۲.۵ میلیمتر،۱۵ آمپر مجاز میباشد که این بخشنامه بر اساس فرکانس استاندارد برق شبکه یعنی ۵۰ هرتز دلالت دارد….سوال اینکه همین سیم در فرکانس زیره ۵۰ کیلو هرتز،تا چه جریان مجازی را به ما تحویل خواهد داد؟؟؟طرح رابطه ای که بتوان از طریق آن محاسبه ی چگالی جریان یک سیم با متریال مشخص،در فرکانس های متفاوت را محاسبه و از آن بهره برداری کرد!!!
برای تعیین جریان مجازی که سیم می تواند در فرکانس 50 کیلوهرتز ارسال کند، می توانیم از چگالی جریان استاندارد مجاز برای سیم های 50 هرتز استفاده کنیم. نکته کلیدی در اینجا در نظر گرفتن اثر پوستی است که در فرکانس های بالاتر قابل توجه می شود. اثر پوستی باعث می شود که سطح مقطع موثر هادی در فرکانس های بالاتر کاهش یابد.
بیایید جریان مجازی را با استفاده از مراحل زیر محاسبه کنیم:
1. عمق پوست (δ) را در فرکانس داده شده پیدا کنید. عمق پوست معیاری است که نشان می دهد جریان تا چه حد در یک فرکانس خاص به داخل سیم نفوذ می کند. توسط:
δ = √(2 / (π * μ * σ * f))
جایی که:
δ عمق پوست است.
μ نفوذپذیری ماده است (برای مس، تقریباً 4π x 10^(-7) H/m است).
σ رسانایی ماده است (برای مس، تقریباً 5.8 x 10^7 S/m است).
f فرکانس (50 کیلوهرتز در این مورد) است.
2. سطح مقطع موثر سیم را برای فرکانس 50 کیلوهرتز محاسبه کنید:
A_effective = A * e^(-d/δ)
جایی که:
A سطح مقطع اصلی است (2.5 mm^2 در این مورد).
d عمق نفوذ (معمولاً برابر با شعاع سیم) است.
3. جریان مجازی (I_virtual) را با استفاده از سطح مقطع موثر و چگالی جریان استاندارد برای 50 هرتز محاسبه کنید:
I_virtual = A_effective * J
جایی که:
J چگالی جریان استاندارد (15 A/mm^2 برای 50 هرتز) است.
بیایید محاسبات را انجام دهیم:
ابتدا عمق پوست (δ) را محاسبه کنید:
δ = √(2 / (π * (4π x 10^(-7)) * (5.8 x 10^7) * 50000))
δ ≈ 0.0263 میلی متر
سپس، سطح مقطع موثر (A_effective) را با استفاده از شعاع سیم (r) 1.25 میلی متر محاسبه کنید:
A_effective = (2.5 mm^2) * e^(-1.25 mm / 0.0263 mm)
A_effective ≈ 0.0207 mm^2
در نهایت جریان مجازی (I_virtual) را محاسبه کنید:
I_virtual = (0.0207 mm^2) * (15 A/mm^2)
I_virtual ≈ 0.3105 A
بنابراین، در فرکانس 50 کیلوهرتز، سیم جریان مجازی تقریباً 0.3105 آمپر را ارائه می دهد.
هرچه مدت زمان رخ دادن واقعهای که به طور پیوسته تکرار میشود (در اینجا چشمک زدن دایرهها) کمتر باشد، فرکانسِ آن بیشتر است.
این جمله اشتباه نیست؟
سلام و روز شما به خیر؛
چون فرکانس برابر با عکس دوره تناوب است، هر چه دوره تناوب کمتر باشد فرکانس بیشتر است. به همین دلیل جملهای که عنوان کردهاید درست است و میتوانید آن را در مثالهای مربوط به چراغ چشمک زن نیز درک کنید.
از اینکه با فرادرس همراه هستید خرسندیم.
سلام ميشه راهنمايي كنين فركانس لحظه اي سيگنال پيوسته چه طور حساب ميشه؟؟
سلام.
فرکانس لحظهای با فرمول زیر محاسبه میشود:
f(t)=2π1ω(t)=2π1dtdφ(t)
که در آن، φ(t) زاویه فاز لحظهای باز نشده است.
موفق باشید.
عالی بود ممنونم
سلام ، ممنون از مطالب آموزنده و بسیار عالی ، ولی چطور میتونم این مقالات و یا کتابها رو دانلود کنم تا در مواقعی که دستزسی به اینترنت نیست هم از آنها استفاده کنم
ممنون عالی بود مفاهیم با ساده ترین بیان منتقل شده
کامل و ساده بود در کل عالی