مرکز جرم – به زبان ساده

مرکز جرم یک جسم، نقطه‌ تعادل آن جسم را نشان می‌دهد. به صورت ریاضی می‌توان بیان کرد که مرکز جرم، نقطه‌ای از جسم در نظر گرفته می‌شود که مجموع گشتاور ناشی از اجزای جرم جسم حول آن نقطه برابر با صفر باشد. مرکز جرم از آن نظر حائز اهمیت است که در مسائل مختلف، می‌توان مجموعه‌ای از اجرام را مانند یک جرم در نظر گرفت که در نقطه مرکز جرم آن‌ مجموعه قرار دارد.

این موضوع کاربرد بسیار زیادی در علم مکانیک و فیزیک دارد. برای مثال قانون دوم نیوتون برای مجموعه‌ای از اجرام با استفاده از این مفهوم، به سادگی قابل بیان است.

این مطلب، ابتدا به بررسی مفهوم مرکز جرم و رابطه کلی آن می‌پردازد. سپس مفهوم تقارن و انواع آن، برای یافتن مکان مرکز جرم یک جسم، بدون انجام محاسبات ریاضی، مورد ارزیابی قرار می‌گیرد. در ادامه رابطه‌ای برای یافتن مکان مرکز جرم چند جسم که روی یک خط یا موقعیت‌های مختلف قرار دارند، ارائه می‌گردد. پس از آن، رابطه مرکز جرم برای اجسام پیوسته با چگالی یکنواخت و متغیر مورد بررسی قرار می‌گیرد و در نهایت تفاوت دو مفهوم اساسی یعنی مرکز گرانش و جرم بیان می‌شود.

مرکز جرم

به صورت کلی می‌توان بیان کرد که مرکز جرم، مکانی است که در آن، مجموع گشتاورها در جهت عقربه‌های ساعت حول مرکز جرم با مجموع گشتاور‌ها در خلاف جهت عقربه‌های ساعت حول همان نقطه، برابر است.

عبارت بالا را می‌توان این گونه بیان کرد که اگر تمام جرم‌های یک مجموعه شامل چند جسم را در مرکز جرم قرار دهیم، گشتاور حاصل از جرم‌های قرار داده شده در مرکز جرم، حول هر نقطه‌ای از فضا با مجموع گشتاور حاصل از تک تک جرم‌ها حول همان نقطه، برابر خواهد بود. این موضوع با استفاده از رابطه زیر نشان داده شده است.

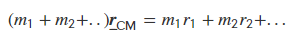
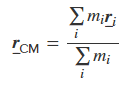
مقدمه‌ای بر تقارن

مرکز جرم یک جسم که چگالی یکنواختی دارد را معمولا بدون انجام محاسبات ریاضی و تنها با در نظر گرفتن تقارن آن جسم، می‌توان به دست آورد.

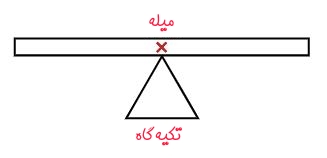
برای مثال یک میله با چگالی یکسان را در نظر بگیرید. واضح است که مرکز جرم این جسم در میانه آن قرار دارد. این موضوع در شکل زیر به تصویر کشیده شده است.

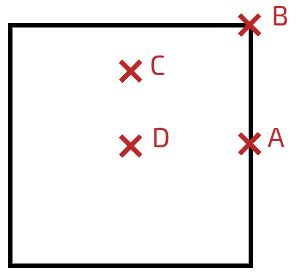
به عنوان مثال دیگر می‌توان مربعی به شکل زیر را در نظر گرفت، مرکز جرم این جسم دو بعدی که چگالی آن یکنواختی است، در نقطه D قرار دارد.

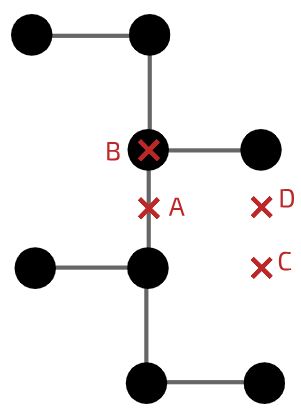
مرکز جرم جسمی با هندسه نشان داده شده در شکل زیر، در نقطه B قرار دارد. توجه شود که چگالی این جسم به صورت یکنواخت در نظر گرفته شده است.

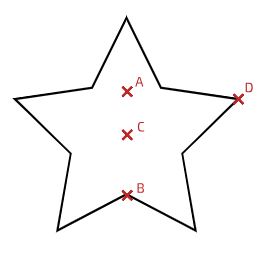
به عنوان مثال سوم، یک ستاره پنج پر را مطابق شکل زیر، در نظر بگیرید. در صورتی که چگالی این ستاره به صورت یکنواخت در نظر گرفته شود، مرکز جرم آن دقیقا در مرکز جسم یعنی نقطه C قرار خواهد گرفت.

تقارن چرخشی

تقارن چرخشی، یکی از پایه‌ای‌ترین انواع تقارن‌ها است که برای محاسبه مرکز جرم یک جسم مورد استفاده قرار می‌گیرد. بنابراین در صورتی که یک جسم و یا مجموعه‌ای از اجسام، حول یک نقطه به صورت چرخشی دارای تقارن باشند، آن نقطه، مرکز جرم آن جسم و یا جسم‌ها است.

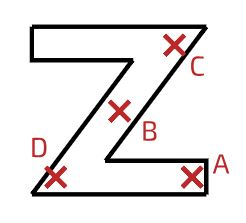
بر این اساس، جسمی که به شکل Z در قسمت قبلی نشان داده شد را اگر 180 درجه حول مرکز آن دوران دهیم، دقیقا مشابه حالت اول خواهد بود. بنابراین مرکز جرم آن دقیقا روی مرکز تقارن چرخشی آن قرار خواهد گرفت.

جسمی را مطابق شکل زیر با چگالی یکنواخت در نظر بگیرید. از آنجایی که این جسم حول نقطه A تقارن چرخشی دارد، مرکز جرم آن، دقیقا همان نقطه A است.

تقارن بازتابی

همانطور که می‌دانید، اگر جسمی، یک خط تقارن بازتابی داشته باشد، با قرار دادن آینه روی خط تقارن می‌توان نیمه پاک شده جسم را بازسازی کرد. مشابه با تعریف یک خط تقارن بازتابی، می‌توان اجسامی را تصور کرد که مانند شکل زیر چند خط تقارن بازتابی داشته باشند.

مرکز جرم‌ یک جسم و یا مجموعه‌ای از اجسام که چند خط برای تقارن بازتابی دارند، دقیقا روی تقاطع این خطوط قرار می‌گیرد و اگر یک جسم، تنها یک خط تقارن بازتابی داشته باشد، می‌توان نشان داد که مرکز جرم‌ این جسم در مکانی روی این خط قرار دارد. برای مثال، ستاره نشان داده شده در شکل بالا را در نظر بگیرید، همه خطوط تقارن بازتابی آن از یک نقطه می‌گذرند که این نقطه همان مرکز جرم‌ این جسم را نشان می‌دهد.

نکته‌ای که باید به آن اشاره کرد این است که در صورتی که یک جسم، دو خط تقارن بازتابی داشته باشد، نقطه‌ تقاطع این دو خط که مرکز جرم‌ آن جسم است، همان نقطه‌ای است که جسم حول آن تقارن چرخشی دارد. توجه شود که معمولا در مسائل مختلف، خط تقارن بازتابی کاربرد بیشتری برای محاسبه مرکز جرم نسبت به نقطه تقارن چرخشی دارد.

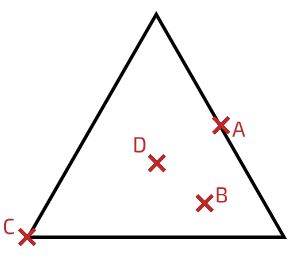
به عنوان مثال، مثلث متساوی الاضلاع با چگالی یکنواخت مانند شکل زیر را در نظر بگیرید. همانطور که مشاهده می‌شود، این مثلث سه خط تقارن بازتابی دارد و مرکز جرم آن دقیق در نقطه تقاطع این سه خط، یعنی در نقطه D قرار می‌گیرد.

مرکز جرم چند جسم روی یک خط

مرکز جرم به صورت کلی، مکانی در فضا است که با سه مولفه y ،x و z معرفی می‌شود، اما زمانی که اجسام روی یک خط قرار داشته باشند، تنها با یک مولفه می‌توان به راحتی مکان مرکز جرم را معرفی کرد. این موضوع به آن دلیل است که در شرایط بیان شده،‌ قرار گرفتن مرکز جرم در نقطه‌ای روی همان خط امری بدیهی است و ما تنها به دنبال یافتن مکان دقیق قرارگیری مرکز جرم روی آن خط هستیم.

برای مثال، مجموعه‌ای از اجسام با جرم یکسان m را در نظر بگیرید که روی یک خط افقی مانند شکل زیر قرار گرفتند. مکان قرارگیری این اجسام به ترتیب در نقاط x=0.25m ،x=0m و x=1m است. این فواصل نسبت به نقطه‌ای در سمت چپ خط، داده شده است.

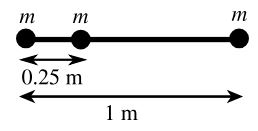
مرکز جرم مجموعه اجسامی که روی یک خط قرار گرفتند با استفاده از رابطه زیر قابل محاسبه است.

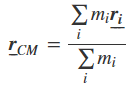
در این رابطه m_i، جرم هر یک از اجسام را نشان می‌دهد و r_i فاصله اجسام از یک مبدا مشخص را بیان می‌کند. بنابراین صورت کسر نشان داده شده در رابطه فوق (رابطه ۳) را می‌توان برای مثال بالا، به شکل زیر بازنویسی کرد.

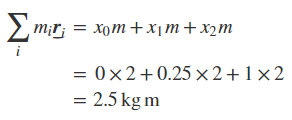
مخرج معادله مرکز جرم (رابطه ۳) نشان دهنده مجموع جرم اجسام حاضر در مسئله است. این عبارت را برای مثال بیان شده، می‌توان به شکل زیر بازنویسی کرد.

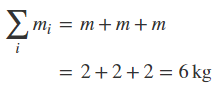
بنابراین می‌توان مکان قرارگیری مرکز جرم این مجموعه از اجسام را با استفاده از قرار دادن مقادیر بالا در رابطه ۳، به شکل زیر محاسبه کرد.

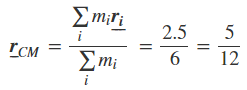
بنابراین مرکز جرم مجموعه اجسام نشان داده شده، در نقطه‌ای روی خط و در فاصله $${5 \over 12} m$$ از سمت چپ مجموعه قرار دارد.

مرکز جرم چند جسم در حالت کلی

فرض کنید، مجموعه‌ای شامل چند جسم موجود است که این اجسام روی یک خط قرار ندارند. در این حالت، باید از سه مولفه y ،x و z برای نمایش مرکز جرم استفاده کرد. رابطه هرکدام از این مولفه‌ها، مشابه با رابطه ۳ است. در واقع در تمام حالات، صورت کسر مرکز جرم به صورت مجموع حاصل ضرب جرم هر جسم در مکان آن است و مخرج آن مجموع جرم تمام اجسام را نشان می‌دهد.

در این حالت، مختصات مرکز جرم با استفاده از روابط زیر قابل محاسبه است. این روابط به ترتیب مکان مرکز جرم را در سه راستای y ،x و z نمایش می‌دهد.

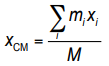
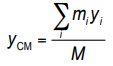
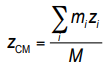
به عنوان مثال، سه جسم با جرم‌های m1 ،m0 و m2 را مطابق شکل زیر در نظر بگیرد. این اجسام به صورت دو بعدی و در یک صفحه، کنار یکدیگر قرار گرفتند و مولفه z تمام آن‌ها یکسان است. بنابراین می‌توان نتیجه گرفت که مرکز جرم آن‌ها روی همین صفحه قرار دارد و نیاز به محاسبه مولفه z مرکز جرم (رابطه 6) نیست.

همانطور که بیان شد، مولفه x مرکز جرم با استفاده از رابطه زیر قابل محاسبه است.

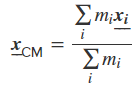
صورت و مخرج رابطه بالا (مولفه x مرکز جرم) برای مجموعه اجسام نشان داده شده، به شکل زیر محاسبه می‌شود.

$$\large \begin{array}{c} \sum_{i} m_{i} \underline{x}_{i}=x_{1} \cos \theta_{1} m_{1}+\left(x_{1} \cos \theta_{1}+x_{2}\cos \theta_{2}\right) m_{2} \\ \sum_{i} m_{i}=m_{0}+m_{1}+m_{2} \end{array}$$

مشابه روندی که برای مولفه x مرکز جرم در بالا طی شد، مولفه y مرکز جرم نیز قابل محاسبه است. این مولفه با استفاده از روندی که در ادامه بیان می‌شود، به دست می‌آید.

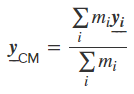
صورت و مخرج رابطه بالا (مولفه y مرکز جرم) برای مجموعه اجسام نشان داده شده، به شکل زیر محاسبه می‌شود.

$$\sum_i m_i y_i = x_ 1 \sin \theta_1 m_1 + (x_1 \sin \theta_1 - x_2 \sin \theta_2) m _ 2$$

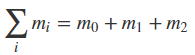
زوایای نشان داده شده در روابط بالا، همان زوایایی است که شکل این مثال بیان شدند.

بنابراین در مجموع با استفاده از روابط نشان داده شده، فرم نهایی مختصات مکان مرکز جرم به شکل زیر نشان داده می‌شود.

$$\large \underline{x}_{\mathrm{CM}}=\frac{x_{1} \cos \theta_{1} m_{1}+\left(x_{1} \cos \theta_{1}+x_{2}\cos \theta_{2}\right) m_{2}}{m_{0}+m_{1}+m_{2}}$$

$$y_CM = \frac{x_1 \sin \theta_1 m_1 + (x_1 \sin \theta_1 - x_2 \sin \theta_2 ) m _2}{m_0 + m_1 + m_2}$$

مرکز جرم اجسام پیوسته

مرکز جرم یک جسم با چگالی یکنواخت را می‌توان به صورت کلی با استفاده از رابطه زیر محاسبه کرد.

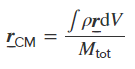
در این رابطه، ρ چگالی جسم را نمایش می‌دهد و V نشان دهنده حجم جسم مورد نظر است. نکته‌ای که باید به آن اشاره کرد این است که زمانی که چگالی یکنواخت باشد، به عنوان یک ثابت از عبارت انتگرالی فوق خارج می‌شود.

در صورتی که چگالی جسم یکنواخت نباشید و مقدار آن در مکان‌های مختلف متفاوت باشد، رابطه انتگرالی فوق به شکل زیر بازنویسی می‌شود.

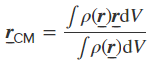
زمانی که شتاب گرانش در محیط به صورت یکسان در نظر گرفته شود، مرکز جرم و «مرکز گرانش» (Centre of Gravity) یکسان خواهند بود. در این حالت می‌توان فرض کرد که مرکز جرم، مکانی از جسم است که اگر تکیه‌گاه را زیر آن نقطه قرار دهیم جسم در حالت تعادل باقی خواهد ماند. در این حالت، گشتاور‌های ساعتگرد و پادساعتگرد حول تکیه‌گاه یکسان خواهند بود.

نکته مهمی که باید به آن اشاره کرد این است که در مسائل مختلف، می‌توان کل جرم جسم را روی مرکز جرم آن جسم متصور شد. بنابراین با استفاده از این کار، محاسبات به فرم بسیار ساده‌تری در می‌آیند.

به عنوان مثال میله‌ای با چگالی M/L را مطابق شکل زیر در نظر بگیرد. در این رابطه M، جرم کلی میله و L، طول آن را نمایش می‌دهد.

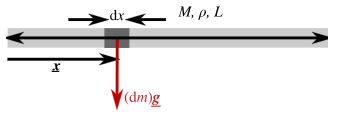
در این شرایط می‌توان میله را با یک نقطه به جرم M نمایش داد که در نقطه‌ای با مختصات r قرار گرفته است و r مکان مرکز جرم این میله را نشان می‌دهد. در شرایطی که میله چگالی یکنواخت دارد، مرکز جرم (فاصله r) در فاصله‌ای برابر با نصف طول میله (r = L/2) قرار می‌گیرد. این موضوع در شکل زیر به تصویر کشیده شده است.

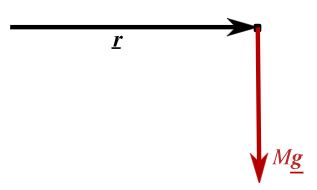
مرکز جرم این میله با استفاده از روابط زیر قابل محاسبه است. ابتدا گشتاور وزن نقطه‌ای که نماینده میله است (شکل بالا) را حول مبدا مختصات می‌نویسیم و مقدار آن را با گشتاور وزن کل میله حوله مبدا مختصات برابر قرار می‌دهیم. این موضوع در رابطه زیر نمایش داده شده است.

r در این رابطه مکان مرکز جرم میله را نمایش می‌دهد. در ادامه، طرفین رابطه بالا را بر وزن کل میله یعنی (Mg) تقسیم می‌کنیم. بنابراین داریم:

با محاسبه انتگرال فوق، مکان مرکز جرم به شکل زیر محاسبه می‌شود.

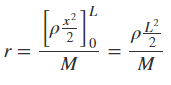
از آنجایی که چگالی در این مثال برابر با M/L بیان شده است، می‌توان نتیجه گرفت که مرکز جرم از رابطه بالا برابر با r = L/2 به دست می‌آید.

تفاوت مرکز جرم و مرکز گرانش

بسیاری از افراد تصور می‌کنند که مرکز جرم و مرکز گرانش، دو مفهوم یکسان هستند، در حالی که این تصوری اشتباه است. در واقع همانطور که اشاره شد، مرکز جرم، نقطه‌ای است که جرم جسم در آن نقطه در حالت تعادل قرار دارد و به میدان گرانش بستگی ندارد.

مرکز گرانش نیز نقطه‌ای را نشان می‌دهد که گشتاور وزن جسم در جهت ساعتگرد و پادساعتگرد حول آن نقطه، یکسان هستند. در واقع اگر یک تکیه‌گاه را در نقطه مرکز گرانش یک جسم قرار دهیم، جسم در حالت تعادل قرار می‌گیرد و دوران نمی‌کند.

نکته مهمی که باید به آن اشاره کرد این است که اگر میدان گرانش به صورت یکنواخت حضور داشته باشد، مرکز گرانش و جرم یک جسم در نقطه‌ یکسانی قرار می‌گیرند. در واقع در بسیاری از مسائل رایج، این موضوع برقرار است و با تقریب خوبی می‌توان مکان این دو نقطه را یکسان در نظر گرفت ولی توجه کنید که مفهوم و تعریف آن‌ها یکسان نیست.

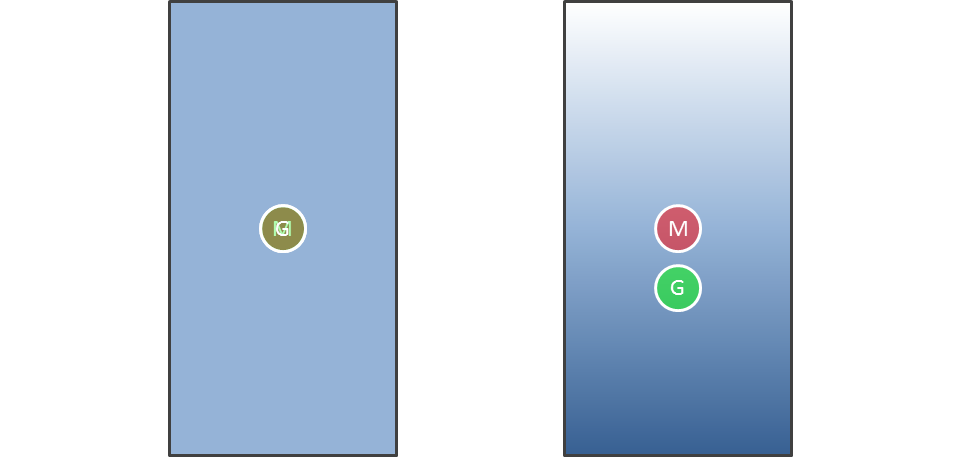
حالتی را در نظر بگیرید که در آن، میدان گرانش در پاهای شما قوی‌تر از مقدار آن در قمست سر شما باشد. در این حالت، مرکز گرانش شما در نقطه‌ای پایین‌تر از مرکز جرم شما قرار دارد. در حالت برعکس، یعنی زمانی که میدان گرانش طوری توزیع شده باشد که مقدار آن در ناحیه سر شما بیشتر از پاهای شما باشد، مرکز گرانش شما بالاتر از مرکز جرمتان قرار خواهد گرفت.

این موضوع در شکل زیر به تصویر کشده شده است. در شکل سمت چپ، جسم نشان داده شده، یک میدان گرانش یکنواخت را تجربه می‌کند و میدان گرانش و جرم این جسم روی یکدیگر قرار گرفته‌اند. در شکل سمت راست، میدان گرانش در پایین جسم قوی‌تر از مقدار آن در بالای جسم است و در نتیجه مرکز گرانش در نقطه‌ای پایین‌تر از مرکز جرم قرار می‌گیرد.

همانطور که اشاره شد، مرکز جرم‌ مکانی است که در آن، مجموع گشتاور جرم‌ها در جهت عقربه‌های ساعت حول نقطه مرکز جرم‌ برابر با مجموع گشتاور‌ها در خلاف جهت عقربه‌های ساعت، حول آن نقطه است و می‌توان این نقطه را مکانی در نظر گرفت که جسم، در آن نقطه، در حالت تعادل قرار دارد.

این مطلب ابتدا مفهوم مرکز جرم و رابطه کلی آن را مورد مطالعه قرار داده است. سپس مفهوم تقارن و انواع آن، برای یافتن مکان مرکز جرم یک جسم، بدون انجام محاسبات ریاضی، ارزیابی شدند. در ادامه، رابطه‌ای بیان شد که به کمک آن، مکان مرکز جرم چند جسم که روی یک خط یا موقعیت‌های مختلفی قرار دارند، قابل محاسبه است. پس از آن، رابطه مرکز جرم برای اجسام پیوسته با چگالی یکنواخت و متغیر بیان شد و در نهایت تفاوت دو مفهوم اساسی یعنی مرکز گرانش و جرم مورد بررسی قرار گرفت.

در صورتی که به مباحث ارائه شده، علاقه‌مند هستید و قصد یادگیری در زمینه‌های مطرح شده در ریاضیات، فیزیک پایه و مکانیک را دارید، آموز‌ش‌های زیر به شما پیشنهاد می‌شود:

• آیرودینامیک (Aerodynamics) چیست؟ — از صفر تا صد
• قوانین حرکت نیوتن — به زبان ساده

^^