فرمول هرون — به زبان ساده

پیشتر، در مجله فرادرس با مثلث و محاسبات مربوط به آن در هندسه آشنا شدیم. در این آموزش، چگونگی محاسبه مساحت مثلث را با استفاده از اضلاع آن بررسی میکنیم.
«فرمول هرون» (Heron's formula) که با نامهای «قضیه هرون» و «دستور هرون» نیز شناخته میشود، فرمولی است که با استفاده از آن میتوان مساحت یک مثلث را با داشتن طول اضلاع محاسبه کرد. این فرمول را میتوان برای هر نوع مثلثی بهکار برد. این فرمول را «هرون اسکندرانی» (Hero of Alexandria)، مهندس و ریاضیدان یونانی در 70-10 میلادی معرفی کرد.
طبق فرمول هرون، مساحت یک مثلث با اضلاعی بهطول b ،a و c را میتوان با رابطه زیر محاسبه کرد:
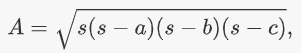
که در آن، s برابر با نصف محیط (مجموع طول سه ضلع) مثلث است:
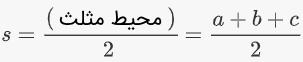
فرمول هرون، به فرمهای دیگری نیز نوشته میشود:

اثبات: همانطور که میدانیم، مساحت یک مثلث برابر با نصف حاصلضرب قاعده در ارتفاع آن است:
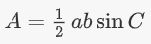
با استفاده از قانون کسینوسها، عبارت زیر را داریم:
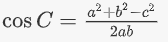
اگر از قضیه فیثاغورس کمک بگیریم، میتوانیم کسینوس بالا را به سینوس تبدیل کنیم:
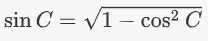
با جایگذاری مقدار سمت راست معادله در رابطه اخیر و قرار دادن این رابطه در فرمول مساحت، بعد از چند عملیات جبری ساده، فرمول هرون اثبات میشود.
مثال
مساحت مثلث زیر را بهدست آورید.
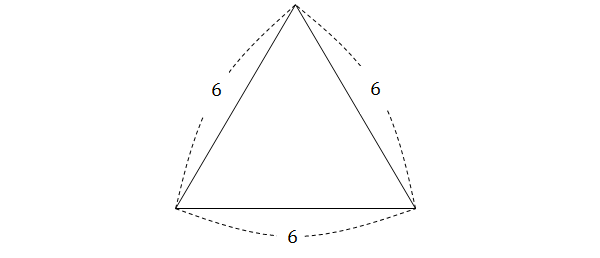
حل: از آنجایی که طول هر سه ضلع مثلث 6 است، نصف محیط آن برابر است با . بنابراین، مساحت بهسادگی و به صورت زیر بهدست میآید:
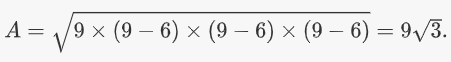
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مثلث — انواع مثلث و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مثلث چیست ؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)
- مساحت انواع مثلث چگونه بدست می آید ؟ — حل تمرین و مثال های متنوع
- محیط مثلث چگونه بدست می آید؟ + فیلم آموزش رایگان
- چگونه مساحت مثلث را حساب کنیم؟ + فیلم آموزشی و تمرین با جواب
- محاسبه آنلاین مساحت مثلث — معرفی بهترین سایتها + مثال
- فرمول محیط مثلث چیست ؟ انواع فرمول ها + حل مثال های متنوع
- فرمول مساحت مثلث چیست ؟ — تمام فرمول ها + حل تمرین
- قاعده مثلث چیست و چگونه بدست می آید ؟ + تعریف و مثال
- ارتفاع مثلث چیست و چگونه رسم می شود ؟ — آموزش تصویری + حل تمرین
- محاسبه ارتفاع مثلث — تعریف، حل تمرین و مثال + جدول فرمول ها
- محیط مثلث مختلف الاضلاع — به زبان ساده + حل مثال های متنوع
- چگونه مساحت مثلث مختلف الاضلاع را حساب کنیم؟ + حل تمرین و مثال
- چگونه مساحت مثلث با سه ضلع معلوم را حساب کنیم؟ + حل تمرین و مثال
- فرمول هرون — به زبان ساده(همین مطلب)
- مساحت مثلث با سینوس چگونه محاسبه می شود ؟ + حل تمرین و جدول فرمول ها
- مثلث قائم الزاویه چیست ؟ — تعریف، ویژگی ها و محاسبات | به زبان ساده
- محیط مثلث قائم الزاویه — به زبان ساده + حل مثال های متنوع
- مساحت مثلث قائم الزاویه — حل تمرین و مثال های متنوع
- مثلث متساوی الساقین چیست ؟ | تعریف، ویژگی ها و محاسبات — به زبان ساده
- محیط مثلث متساوی الساقین — به زبان ساده و با حل مثال
- مساحت مثلث متساوی الساقین — حل تمرین و مثال های متنوع
- محیط مثلث متساوی الاضلاع چگونه بدست می آید؟ + حل مثال و تمرین
- مساحت مثلث متساوی الاضلاع — حل تمرین و مثال های متنوع













عالی بود
خیلی خوبه ???
عالی بود.