رادیکال چیست؟ — قوانین رادیکال به زبان ساده

احتمالا با خواندن مطالب دیگر مجله فرادرس با مفهوم رادیکال آشنا شدهاید. ولی در اینجا قصد داریم به طور مفصل و البته به زبان ساده، بفهمیم که رادیکال چیست و قوانین رادیکال و انجام عملیات روی عبارتهای رادیکالی به چه صورت است.
برای آشنایی بیشتر با رادیکال و نحوه محاسبه آن به مطالب اعداد رادیکالی و محاسبات مربوط به آن ها — به زبان ساده و فرمول رادیکال در اکسل — از صفر تا صد (+) را بخوانید. همچنین نوشتارهای جذر یا محاسبه ریشه دوم عدد — به زبان ساده یا معادله رادیکالی — به زبان ساده از مجله فرادرس نیز خالی از لطف نیست.
رادیکال چیست ؟
«ریشهها» (یا رادیکال ها) یک عملگر ریاضی هستند که عکس عملگر توان (Power) را اجرا میکنند. ما میتوانیم عملی که «توان رساندن» روی یک عدد ایجاد میکند را به کمک «عملگر رادیکال» لغو کنیم و همچنین یک عملگر رادیکال یا جذر را با یک عملگر توانی بیاثر نماییم. به عنوان مثال، اگر عدد ۲ را به صورت مربع (توان ۲) درآوریم، واضح است که مقدار ۴ حاصل میشود. زیرا رابطه زیر برقرار است.
به این ترتیب اگر از عدد 4 جذر یا ریشه دوم بگیریم، عمل توانرسانی (مربع کردن) لغو شده و به همان مقدار قبلی یعنی 2 خواهیم رسید. همینطور اگر 3 را مربع کنیم، 9 حاصل میشود. از طرفی ریشه دوم 9 نیز همان ۳ را نتیجه میدهد. در ریاضیات این عملیات را به صورت زیر نشان خواهیم داد.
نمادی که در بالا به صورت «√» به کار رفته، نماد «رادیکال» نامیده میشود. به این ترتیب گزاره را ریشه دوم یا جذر عدد ۹ یا به طور خلاصه رادیکال ۹ میخوانیم.

ما میتوانیم توان رساندن را به غیر از مربع (توان ۲) نیز انجام دهیم. مکعب یک عدد به معنی به توان رساندن با نمای ۳ است. همچنین میتوانیم اعداد را به توان چهارم یا «به قوه 4» برسانیم، یا حتی توان 100 و غیره. به همین ترتیب، میتوانیم ریشه مکعب یک عدد، ریشه چهارم، ریشه 100ام و غیره را برای یک عدد محاسبه کنیم. همانطور که ریشه دوم، مربع کردن را از بین میبرد، ریشه مکعب نیز مکعب کردن را برطرف میکند، ریشه چهارم نیز باعث از بین بردن توان ۴ یا قوه ۴ یک عدد میشود.
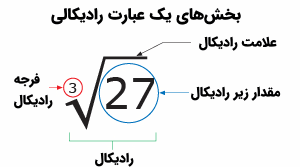
برای نشان دادن برخی از ریشههای دیگر به غیر از یک ریشه مربع، هنگام نوشتن از همان علامت رادیکال یا استفاده میکنیم، اما یک عدد را هم در قسمت بالای رادیکال در نظر میگیریم، این عدد را به شکل کوچکتر از اعداد دیگر و داخل فضای خالی بالای رادیکال مینویسیم. این فضا به نام قسمت فرجه رادیکال شناخته میشود. این عدد مربوط به مقدار ریشهای است که باید گرفته شود. به عنوان مثال، در مورد مکعب کردن و پیدا کردن ریشه سوم برای عدد ۴ و ۶۴ رابطههای زیر را داریم.
عدد «3» در بالای علامت رادیکال نشانگر شاخص یا فرجه رادیکال است. همچنین «64» نیز پارامتر رادیکال است که «عدد زیر رادیکال» نیز نامیده میشود. شاید به این دلیل که بیشتر رادیکالهایی که استفاده میکنیم، براساس ریشه دوم نوشته میشوند، اغلب از بیان فرجه ۲ در رادیکال صرف نظر میشود. ولی توجه داشته باشید که رابطه زیر برای رادیکال با فرجه ۲ و ریشه دوم یا جذر نیز وجود خواهد داشت.
به این ترتیب نامگذاری ریشه یا رادیکالها با توجه به فرجه به صورت زیر خواهد بود.
- ریشه دوم یا جذر، .
- ریشه سوم یا کعب، .
- ریشه چهارم، .
- ریشه پنجم، .
- ...
به یاد داشته باشید که میتوانیم هر عدد را به صورت مربع یا مکعب یا به هر توانی رسانده و سپس از عدد حاصل، جذر، کعب یا رادیکال برحسب فرجه همان توان بگیریم و به عدد اولیه برسیم. این کار را در مثالهای قبلی دیدیم، در ادامه متن، به مواردی اشاره خواهیم کرد که برای مشخص کردن رادیکال اعداد از عکس عمل توان رساندن استفاده کردیم.
همانطور که میدانید، 16 یک عدد مربع است زیرا میتوان آن را برمبنای توان ۲ نمایش داد.
پس ریشه دوم عدد ۱۶ برابر است با ۴.
ولی متاسفانه همیشه نمیتوان رادیکال را به صورت ساده و برحسب توان، محاسبه کرد. برای مثال مقدار ۳ را در نظر بگیرید. در بین اعداد صحیح، عددی وجود ندارد که آن را به توان ۲ رسانده و به مقدار ۳ برسیم.
متاسفانه یک عدد صحیح یا حتی گویا نخواهد بود و باید آن را در بین اعداد حقیقی جستجو کرد. اگر با استفاده از ماشین حساب ریشه دوم عدد ۳ را محاسبه کنید به مقدار زیر خواهید رسید.
عدد حاصل یک عدد گنگ بوده و در نتیجه نمیتوان مقدار دقیق آن را مشخص کرد. بنابراین در اغلب موارد آن را بوسیله عمل گرد کردن، به نزدیکترین عدد گویا گرد کرده و برای محاسبات به کار میگیریم.
از آنجایی که در اغلب موارد با رادیکال با فرجه ۲ یا ریشه دوم اعداد مواجه میشویم، بخش بعدی را به نحوه محاسبه این گونه رادیکالها یعنی ریشه دوم اعداد یا عبارتهای جبری اختصاص میدهیم. ولی در قسمتهای بعدی، نگاهی به رادیکال با فرجههای بزرگتر از ۲ نیز خواهیم داشت. یکی از کاربردهای مهم ریشه دوم یا رادیکال با فرجه ۲، در قضیه فیثاغورس (فیثاغورث) نهفته است.
قضیه فیثاغورس: در یک مثلث قائمالزاویه، مربع وتر، برابر است با مجموع مربعات دو ضلع دیگر. بنابراین اگر طول ضلع وتر را با c و طول اضلاع دیگر را با a و b نشان دهیم، طبق این قضیه، رابطه زیر برقرار است.
به این ترتیب میتوانیم طول ضلع وتر را با محاسبه ریشه دوم مجموع مربعات دو ضلع دیگر از این مثلث بدست آوریم.
نکته: برای مشاهده و آشنایی با نحوه محاسبه ریشه دوم اعداد، بهتر است نوشتار جذر یا محاسبه ریشه دوم عدد — به زبان ساده را مطالعه کنید. در بخش بعدی بیشتر به محاسبات روی عبارتهای رادیکالی تاکید خواهیم کرد.
اگر به مقادیر ریشه دوم اعداد صحیح علاقمند هستید، نگاهی به جدول زیر بیاندازید. در این جدول برای مقادیر ۱ تا ۲۰، ریشه دوم یا همان جذر محاسبه شده و با دقت چهار رقم اعشار نمایش داده شده است.
جدول ۱: ریشه یا جذر اعداد ۱ تا ۲۰
| مقدار | ریشه دوم یا جذر | نتیجه |
| ۱ | 1 | |
| 2 | ۱٫4142 | |
| 3 | 1٫7321 | |
| 4 | ۲ | |
| 5 | 2٫2361 | |
| 6 | 2٫4495 | |
| 7 | ۲٫6458 | |
| 8 | 2٫8284 | |
| 9 | 3 | |
| 10 | 3٫1623 | |
| 11 | 3٫3166 | |
| 12 | 3٫4641 | |
| 13 | 3٫۶۰۵۵ | |
| 14 | 3٫7417 | |
| 15 | 3٫8730 | |
| 16 | 4 | |
| 17 | 4٫1231 | |
| 18 | 4٫2426 | |
| 19 | 4٫3589 | |
| 20 | 4٫4721 |
ساده کردن عبارتهای رادیکال یا جذر
برای ساده سازی عبارتی که حاوی ریشه مربع یا جذر است، باید جملات داخل رادیکال را به صورت «مربع کامل» درآوریم. سپس این بخش را از داخل رادیکال خارج کرده و با گرفتن ریشه دوم از آن، در خارج از رادیکال نمایش دهیم.
به عنوان مثال، مشخص است که عدد 4 همان مربع عدد 2 است، بنابراین ریشه دوم 4 برابر است با ۲، زیرا عدد ۴ از ضرب دو عامل یکسان یا برابر (که در اینجا عدد ۲ است) ساخته شده.
همانطور که در رابطه بالا مشاهده شد، ابتدا ۴ را به صورت یک مربع کامل () نوشتیم، سپس پایه را از داخل رادیکال خارج کردیم زیرا توان با فرجه رادیکال یکسان است. بنابراین عبارت زیر رادیکال (بدون در نظر گرفتن توان آن) از داخل آن خارج خواهد شد. همین عمل را برای عدد ۴۹ نیز تکرار میکنیم.
باز هم میبینید، چون ۴۹ را میتوان به صورت نوشت، توان را با فرجه رادیکال ساده کرده و عدد ۷ را از داخل رادیکال خارج کردهایم. به عنوان یک مورد دیگر به ۲۲۵ اشاره میکنیم. میدانیم که مربع ۱۵ برابر است با ۲۵۵. بنابراین، ریشه دوم ۲۵۵ همان مقدار ۱۵ خواهد بود. این کار را بوسیله مربع کردن عبارت زیر رادیکال به شکل زیر انجام میدهیم، سپس با حذف فرجه با توان، مقدار زیر رادیکال را بیرون میآوریم.

نکته: توجه داشته باشید که مقدار یا نتیجه محاسبه رادیکال، همیشه مقداری مثبت یا نامنفی است. ولی اگر از اعداد منفی چشم پوشی نکرده باشیم، میتوانیم آنها را در محاسبه مربع نیز به کار ببریم. به رابطههای زیر دقت کنید. مشخص است که برای مثال مربع ۲- نبر برابر با ۴ است. ولی هرگز ریشه دوم یا رادیکال ۴ را برابر ۲- قرار نمیدهیم. زیرا همیشه مقدار رادیکال با فرجه زوج، مثبت است.
تأکید میکنیم که ارزیابی یک عبارت برای یافتن مقدار و حل یک معادله به منظور پیدا کردن ریشههای آن، دو چیز کاملاً متفاوت هستند. در حالت اول، درست به مانند عملیات قسمت قبل عمل میکنیم و برای مثال هرگز ریشه دوم مقدار ۴ را با علامت منفی نشان نمیدهیم. ولی اگر برای حل معادله اقدام کنیم، ریشهها را به ترتیب برابر با ۲ و ۲- در نظر میگیریم. زیرا میدانیم، مربع ۲ یا ۲- برابر با ۴ هستند. به این ترتیب به دنبال همه مقادیری هستیم که در معادله صدق میکنند. پس برای این معادله دو ریشه حقیقی پیدا میکنیم که تساوی برایشان برقرار میشود.
همین موضوع نشان میدهد که محاسبه با حل معادله درجه ۲ ممکن است تفاوتهای زیادی داشته باشند. رابطههای زیر را در این حالت در نظر بگیرید.
همانطور که در مثال مربوط به ریشه دوم عدد ۳ اشاره کردیم، اغلب اوقات بدست آوردن نتیجه یک رادیکال به کمک تبدیل به مربع کامل امکانپذیر نیست، اما ممکن است یک مربع در میان عوامل آن وجود داشته باشد. برای ساده سازی این نوع رادیکالها، ما باید استدلال را به کمک فاکتور گیری صورت دهیم. یعنی هر آنچه درون رادیکال است را با توجه به عواملی که به صورت مربع هستند، فاکتور گیری کرده، سپس به سادهسازی رادیکال دست بزنیم.
هنگام انجام این کار، استفاده از این واقعیت مهم است که میتوانیم ضرب رادیکالها را به صورت رادیکال ضرب جملات داخل رادیکال بنویسیم. این موضوع درست مشابه توان رسانی و روشهایی ساده کردن جملات تواندار است. به قواعد زیر توجه کنید.

قاعده ضرب جملات تواندار و تواندار کردن ضرب آنها
به این ترتیب براساس رابطه بالا، برای رادیکال نیز رابطه زیر برقرار است.
قاعده تبدیل ضرب رادیکال به رادیکال ضرب و برعکس
در ادامه برای نشان دادن کاربرد این قاعده، مثالهایی ذکر خواهیم کرد که به درک عملیات مربوط به سادهسازی رادیکالها کمک خواهند کرد.
مثالهای مربوط به سادهسازی رادیکال
در مثالهای پیش رو به وضعیتی خواهیم پرداخت که از قواعد ساده سازی گفته شده در قسمت قبل، برای محاسبه رادیکال استفاده خواهیم کرد.
مثال ۱: مقدار را محاسبه کنید.
برای بدست آوردن رادیکال بالا، از دو شیوه کمک میگیریم. ابتدا ۱۴۴ را به صورت حاصلضرب دو عبارت مربع مینویسیم. مشخص است که رابطه زیر بین ۱۴۴ با ۹ و ۱۶ برقرار است.
میدانیم که ۹ و ۱۶ هر دو مربع کامل هستند. پس عبارت زیر رادیکال را به به صورت حاصلضرب این دو مقدار یعنی مربع کامل مینویسیم.
میتوان مشاهده کرد که از تبدیل رادیکال ضرب به ضرب رادیکال بهره بردهایم.
راه حل دوم آن است که به طور مستقیم، ۱۴۴ را به صورت مربع کامل بنویسیم. همانطور که میدانید مربع ۱۲ برابر است با ۱۴۴، پس در این حالت ۱۲ ریشه دوم ۱۴۴ خواهد بود.
مثال ۲: عبارت را ساده کنید.
اینبار هم از قاعده تبدیل ضرب رادیکالها به رادیکال ضرب استفاده میکنیم و نتیجه را بدست میآوریم.
واضح است که برای بدست آوردن تساوی آخر، به مثال ۱ توجه داشتهایم.
مثال ۳: مقدار را به سادهترین حالت مشخص کنید.
این بار عدد ۷۵ را به صورت تجزیه به عوامل اول در میآوریم. به این ترتیب رابطه یا تساوی زیر حاصل میشود.
منظور از تجزیه به عوامل اول، نوشتن یک عدد، برحسب ضرب اعدادی است که همگی عدد اول باشند.
بنابراین برای محاسبه از این تجزیه کمک میگیریم.
از آنجایی که عبارت یک عبارت یا جمله مربع کامل است، پایه آن از داخل رادیکال خارج میشود و خواهیم داشت:
البته در اغلب موارد دوست داریم که عدد را بر رادیکال مقدم بداریم به همین دلیل ۵ را به صورت ضریب در ابتدای عبارت نوشته و رادیکال را به عنوان عبارت دوم در ضرب به کار میبریم تا به اشتباه رابطه بالا را به صورت به کار نبریم.
نتیجه سمت راست تساوی بالا را به صورت «پنج رادیکال ۳» میخوانیم.
نکته: هنگام نوشتن یک عبارت حاوی رادیکال، فرم مناسب آن است که رادیکال را در انتهای عبارت قرار دهید. ولی باید توجه داشته باشید که عدد قبل از رادیکال را با فرجه رادیکال اشتباه نگیرید. بنابراین همیشه مراقب باشید که فرجه را درست بالای علامت رادیکال قرار دهید تا دچار اشتباه نشوید.
هنگام ساده سازی لازم نیست که عبارت زیر رادیکال را تا انتهای اعداد اول فاکتور بگیرید. به محض اینکه میبینید یک عامل یا مضربی به شکل مربع کامل دارید و آنچه باقی میماند، قابلیت تبدیل به مربع کامل را ندارد، دست نگه داشته و نتیجه را به صورت حاصل ضرب نمایش میدهیم.
مثال ۴: را به سادهترین حالت بنویسید.
ابتدا سعی میکنیم بخش مربع کامل را از ۷۲ استخراج کنیم.
همانطور که مشخص است از مربع کامل یعنی عدد ۳۶ در تجزیه ۷۲ کمک گرفته و نتیجه را به صورت ضرب عدد در رادیکال نمایش دادیم.
نکته: توجه دارید که ۲ مربع کامل نیست و از رادیکال خارج نمیشود.

مثال ۵: مقدار را مشخص کنید.
ابتدا با فاکتورگیری آغاز میکنیم. از آنجایی که در عدد ۴۵۰۰، به تعداد ۴۵ دسته ۱۰۰ تایی وجود دارد (۱۰۰ نیز مربع کامل است) عبارت را به صورت زیر تجزیه میکنیم.
از نتیجه حاصل برای محاسبه رادیکال استفاده خواهیم کرد. در گام دوم سعی میکنیم که ۴۵ را به صورت حاصلضرب عبارتهای مربع کامل بنویسیم. پس میتوان نوشت:
پس در حالت کلی از رابطه زیر استفاده خواهیم کرد.
میدانید که منظور از همان حاصلضرب ۳۰ در رادیکال ۵ است ولی نمایش آن را بدون علامت ضرب انجام میدهیم.
در بخش بعدی به بررسی جملات و عبارتهای جبری و ریشه دوم آنها خواهیم پرداخت. مشخص است زمانی که از عبارتهای جبری صحبت میکنیم، پای متغیرها نیز در میان خواهد بود. از آنجایی که متغیرها نیز نماینده اعداد هستند، ریشهگیری یا محاسبه جذر عبارت های جبری به مانند اعداد خواهد بود. ولی برای تاکید و همچنین استفاده از بعضی اتحادها، جذر گیری یا سادهکردن این گونه عبارتها را بازگو خواهیم کرد.
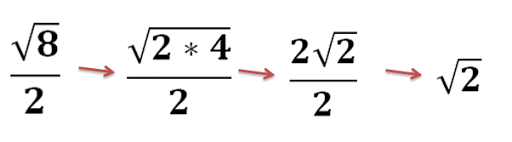
ساده سازی و ضرب جملات زیر رادیکال
هنگام ساده سازی عبارتهای زیر رادیکال، شما همیشه فقط اعداد درون رادیکال را نخواهید داشت. ممکن است یک عبارت رادیکالی با متغیرها نیز همراه باشد. متغیرهای موجود در محاسبه یک رادیکال به همان روش اعداد صورت خواهد گرفت و مبنا، ایجاد جملاتی به صورت مربع کامل یا فاکتورگیری است. برای توضیح مراحل کار به ذکر مثالهایی در این زمینه خواهیم پرداخت.
مثال ۶: عبارت را ساده کنید.
از قبل میدانیم که 16 یک مربع کامل است، بنابراین عدد 4 را از رادیکال خارج میکنیم. با نگاه به بخش متغیر، متوجه میشویم که x نیز به صورت مربع کامل به کار رفته است. بنابراین میتوانیم از متغیر را هم از رادیکال خارج کنیم.
به روند مربوط به این محاسبه که در ادامه دیده میشود، توجه کنید.
عبارتهای طرف راست، مربع کامل هستند و پایهها از رادیکال خارج میشوند.
همانطور که میبینید، سادهسازی رادیکالهایی که شامل متغیرها هستند دقیقاً به همان روش سادهسازی رادیکالهایی است که فقط شامل اعداد هستند. فاکتور گیری یا تبدیل به مربع کامل، راهکارهایی است که در اینجا نیز به کار میروند.
مثال ۷: عبارت را ساده کنید.
از آنجایی که فرجه رادیکال زوج است (اگر رادیکال بدون فرجه باشد، محاسبه ریشه دوم صورت میگیرد) بنابراین تمامی جملات با توان زوج را میتوان به صورت مربع کامل در آورد و از رادیکال خارج کرد. همچنین برای جمله یا عبارتهایی به شکل توانهای فرد نیز میتوان بخشی را به صورت توان زوج و بخش دیگر را به صورت توان فرد در آورد که حاصل ضرب آنها، همان توان عبارت اصلی را بسازد.
همانطور که مشخص است b و c دارای توانهای فرد هستند ولی میتوانیم آنها را به دو بخش ضربی با توانهای زوج و فرد تفکیک کنیم. محاسبات را در ادامه میبینید.
به این ترتیب با خارج کردن عبارتهای مربع کامل، جملات سمت راست ساده شده و به شکل زیر در میآیند.
باز هم میبینید که با ضربکردن اعداد، اعداد را قبل از عبارت رادیکالی قرار دادهایم تا خواندن جمله، سادهتر شود. به این ترتیب حاصل را به صورت «دو آ دو، بی سه ،سی در رادیکال سه بی سی» میخوانیم.
مثال ۸: عبارت را ساده کنید.
به وسیله فاکتورگیری و استفاده از تفکیک توانها عبارتهای مربوط به متغیرهای r و s را جدا کرده تا به صورت مربع کامل درآیند. این عملیات در رابطههای زیر اجرا شدهاند.
نکته: ممکن است اشاره شده باشد که مقدار متغیرهای s , t مثبت هستند. این امر به جهت مثبت بودن مقدار زیر رادیکال مهم است. به یاد دارید که مقادیر زیر رادیکالهای با فرجه زوج، همیشه باید مثبت باشند.
ضرب رادیکال ها
اولین کاری که برای سادهسازی رادیکالها به کار بردید، استفاده از تبدیل رادیکال ضرب به ضرب رادیکالها بود. حال میخواهیم عمل عکس را انجام دهیم و برای سادهسازی ضرب رادیکالها، آنها را به رادیکال ضرب تبدیل کرده و جملهها را ساده کنیم.

ساده سازی رادیکالهای ضرب شده بسیار ساده است، ما از این واقعیت استفاده میکنیم که ضرب دو رادیکال همان رادیکال ضرب است و بالعکس. برای روشن شدن موضوع به ذکر مثالهایی خواهیم پرداخت.
مثال 9: حاصل ضرب را انجام دهید.
همانطور که میدانید، این ضرب رادیکالها است و چون فرجه رادیکالها یکسان است میتوانیم ضرب رادیکالها را به صورت رادیکال ضرب عبارتهای زیر رادیکال بنویسیم.
همین عمل را به کمک تجزیه نیز میتوانیم اجرا کنیم. به روابطی که در زیر قابل مشاهده است دقت کنید.
کاملا مشخص است که ابتدا ۸ را تجزیه کردهایم و به عاملی به صورت مربع درآوردهایم. سپس ضرب دو رادیکال یکسان را ساده کرده و چون هر دو عبارت رادیکالی یکسان هستند، رادیکال را برداشتهایم.
نکته: همانطور که در مثال قبل مشاهده کردید، هنگامی که یک رادیکال به توان ۲ (مثل ) برسد، رادیکال از بین میرود. بنابراین میتوان گفت که چه مقدار زیر رادیکال یا کل عبارت (با رادیکال) به توان ۲ برسد، رادیکال از بین خواهد رفت.
مثال ۱۰: عبارت با چه مقداری برابر است؟
به منظور محاسبه عبارت گفته شده، ابتدا ضرب رادیکالها را به رادیکال ضرب تبدیل میکنیم.
مثال ۱۱: عبارت را ساده کنید.
درست به مانند مراحل قبلی، اعداد را به صورت تجزیه به عوامل اول یا مربع کامل در میآوریم.
بنابراین جذر یا ریشه حاصل ضرب را مینویسیم.
مثال ۱۲: عبارت را ساده کنید.
میبینید که در کنار اعداد از متغیرها نیز استفاده شده است. مشخص است که ۴ خود یک مربع کامل است و از درون حاصل ضرب در نیز میتوان بخش مربع کامل را استخراج کرد. بنابراین محاسبات را به صورتی که در ادامه میبینید، پی میگیریم.
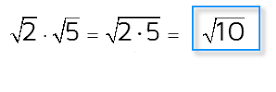
جمع و تفریق رادیکال ها
درست مانند اعداد گویا، ریشهها یا اعداد رادیکالی را میتوان با هم جمع یا تفریق کرد. البته ممکن است عمل سادهسازی نتیجه جمع یا تفریق قابل اجرا نباشد. از طرفی به این موضوع نیز توجه داشته باشید که رادیکالها برای جمع یا تفریق باید دارای فرجه یکسانی بوده و در عین حال، مقدار زیر رادیکال نیز برایشان برابر باشد.

به این ترتیب باید جملات مشخص برای جمع و تفریق رادیکالی، مشابه باشند. پس بهتر است تعریفی از اعداد یا عبارتهای رادیکالی مشابه ارائه دهیم. زیرا دو عدد رادیکالی را زمانی میتوان با یکدیگر جمع جبری کنیم که مشابه باشند.
رادیکال های مشابه: اعداد رادیکالدار، زمانی مشابه هستند که فرجه و مقدار زیر رادیکال در آنها برابر بوده و تنها میتواند ضریب رادیکالها با یکدیگر تفاوت داشته باشند. در جمع و تفریق اعداد رادیکالی این موضوع اهمیت پیدا میکند زیرا فقط رادیکال های مشابه را میتوان از هم تفریق یا با هم جمع کرد.
برای مثال و مشابه هستند، زیرا فرجه هر دو رادیکال ۲ بوده و از طرفی مقدار زیر رادیکال در هر دو عدد برابر با ۳ است. اعداد ۴ و ۵و نیز ضریبهای رادیکالها هستند. بنابراین اگر قرار باشد آنها را با یکدیگر جمع یا تفریق کنیم، رابطهها را به صورت زیر خواهیم نوشت.
همچنین برای تفریق نیز به صورت زیر عمل خواهیم کرد.
بنابراین قاعده کلی برای جمع یا تفریق دو عدد رادیکال (ریشه دوم) با ضرایب مختلف را به صورت زیر خواهیم داشت:
همچنین یکسان بودن فرجهها را هم باید در نظر گرفت. برای مثال اگر ریشه ام عدد مطرح باشد، رابطه بالا به صورت کلی به شکل زیر خواهد بود.
نکته: اگر در عبارت اول، فرجه و در عبارت دوم، فرجه بوده که ، آنگاه امکان جمعکردن این جمله وجود نخواهد داشت. همچنین اگر در عبارت اول و در عبارت دوم مقدار زیر رادیکال باشند، بطوری که آنگاه امکان جمع جبری جملات وجود ندارد.
در ادامه به ذکر مثالهایی در این زمینه میپردازیم تا مسئله جمع و تفریق رادیکال برایتان روشنتر شود.
مثال ۱۳: عبارت زیر را ساده کنید.
از آنجایی که هر دو عبارت در جمع، رادیکال با فرجه ۲ هستند و مقدار زیر رادیکال نیز یکسان است، امکان محاسبه جمع جبری وجود دارد. در این حالت به صورت زیر عمل میکنیم.
مثال ۱۴: نتیجه جمع رادیکال ۹ و رادیکال ۲۵ چیست؟
در حقیقت مسئله را به بیان ریاضی به شکل زیر مشخص میکنیم.
نکته: توجه داشته باشید که در رابطه بالا، ابتدا رادیکالها ساده شده، سپس با یکدیگر جمع شدهاند. واضح است که رابطه زیر را برای جمع کردن رادیکالها نباید به کار بست.
مثلا طبق مثال ۱۴، داریم:
ولی به این موضوع نیز توجه داشته باشید که ممکن است با ساده کردن رادیکالهایی مانند یا ، به عبارتهایی برسیم که در زیر رادیکال، مقدارهای زیر رادیکال برابر شده و با توجه به یکسان بودن فرجهها، جمع یا تفریق میسر شود. مثالهای قبلی به این موضوع پرداخته بودند. در ادامه به مثالهای دیگری اشاره میکنیم که در آنها، یا جملات مشابه وجود دارند یا به کمک تغییراتی میتوان به جملات مشابه برای محاسبه رادیکال، رسید.
مثال ۱۵: نتیجه جمع زیر را بدست آورید.
از آنجایی که عبارتهای زیر رادیکال برابر بوده و هر دو برحسب ریشه دوم هستند، امکان جمع کردن وجود دارد. پس نتیجه را به صورت زیر محاسبه میکنیم.
مثال ۱۶: نتیجه جمع برای عبارت زیر چیست؟
همانطور که میبینید فقط دو جمله اول و سوم در این مثال مشابه هستند و به این ترتیب و قابل جمع بوده و عبارت نمیتواند با آنها جمع شود.
واضح است که ضریب در عبارت سمت چپ، یعنی برابر با ۱ است. به همین دلیل در ادامه محاسبات، داخل پرانتز، ۱ را با ۳ جمع کردهایم. در مثال بعدی میخواهیم به موارد بیشتری از نحوه جمع یا تفریق جملات رادیکالی بپردازیم.

مثال ۱۷: عبارت زیر را ساده کنید.
برای آنکه به سادهترین حالت نمایش این جمع و تفریق برسیم، مراحل زیر را طی خواهیم کرد.
به این ترتیب با ساده کردن رادیکالها به رابطه زیر خواهیم رسید.
که پس از سادهسازی و جمع جبری رادیکالها مقدار نهایی بدست میآید.
همانطور که در این مثال مشاهد کردید، در ابتدا به نظر میرسید با نابرابری مقادیر زیر رادیکال، امکان جمع یا تفریق وجود ندارد. ولی پس از آنکه عبارتهای رادیکالی را ساده کردیم، به جملات مشابه رادیکالی رسیدیم و توانستیم محاسبات مربوط به جمع و تفریق را برای این جملهها اجرا کنیم.
مثال ۱۸: نتیجه سادهسازی رابطه چه خواهد شد؟
از آنجایی که هر دو رادیکال فرجه یکسانی دارند، امکان سادهسازی و جمع کردن آنها محتمل است. ولی از طرفی، مقادیر زیر رادیکالها یکسان نیستند و امکان سادهسازی نیز وجود ندارد. بنابراین عبارت گفته شده به سادهترین شکل نوشته شده و نمیتوان در آن تغییری بوجود آورد.
مثال ۱۹: حاصل ضرب در را بدست آورید.
از خاصیت پخشی ضرب نسبت به جمع استفاده کرده و رابطه ضرب را ساده میکنیم.
همانطور که مشخص است، نتیجه از این سادهتر نخواهد شد.
مثال ۲۰: حاصل ضرب چیست؟
مثال ۲۱: مقدار حاصل ضرب زیر را بدست آورید.
در این مثال به کمک ضرب جمله به جمله، محاسبات را برای مقادیر رادیکالی اجرا میکنیم و هر بار بخشی از عبارت اول را به صورت پخشی، در عبارت دوم ضرب خواهیم کرد.
مزدوج و تقسیم رادیکال ها
در بخش قبل دیدید که برای ضرب دو عبارت که به صورت جمع رادیکالها نوشته شده، باید از خاصیت پخشی ضرب نسبت به جمع استفاده کنید. ولی در بسیاری از موارد به کمک اتحادها، بخصوص اتحاد مزدوج، این ضربها به سادگی قابل حل هستند.
البته برای آنکه ابتدا بدانیم چگونه این ضربها باید صورت گیرند، همان خاصیت پخشی را به کار برده ولی ضربها را به صورت ستونی یا عمودی انجام میدهیم. این عمل ضرب را هنگامی که اعداد دو رقمی را ضرب میکنیم هم به کار بردهایم. در ادامه این نوع ضرب را به کمک مثالهایی، معرفی میکنیم.
مثال ۲۲: حاصل ضرب را در مشخص کنید.
قاعده ضرب عمودی را برای تک تک جملهها به کار خواهیم برد. به تصویر زیر دقت کنید.
همانطور که میبینید، قسمت اول ضرب در بخش اول دیده می شود و بخش دوم (سطر دوم) از ستون دوم آغاز شده. همین عملیات را به صورت پخشی و سطری نیز میتوان اجرا کرد.
پس از سادهسازی و جمع جبری جملات مشابه به رابطه زیر خواهیم رسید.
مثال ۲۳: ضرب زیر را انجام دهید.
میبینید که پرانتز اول بسیار به پرانتز دوم شبیه است. در حقیقت تنها تفاوت در علامت جمع و تفریق دو پرانتز نهفته است. در این حالت عبارت اول و دوم را «مزدوج» (Conjugate) یکدیگر مینامند. در اینجا عمل ضرب را به مانند قبل انجام میدهیم ولی در ادامه مفهوم ضرب عاملهای مزدوج را به کمک اتحادها اجرا خواهیم کرد.
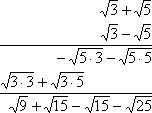
در ضرب بالا که به صورت ستونی نوشته شده، مشخص است که عبارتها، یکی یکی در هم ضرب و سپس با هم جمع شدهاند. پس از جمع جبری به رابطه زیر خواهیم رسید.
نکته: هر دو عبارت اولیه، یک عدد غیرگویا (عدد موهومی) را نشان میدهند در حالیکه حاصلضرب آنها یک عدد گویا (۲-) شد. این امر نشان میدهد که از ضرب دو عدد موهومی میتوان یک عدد گویا ساخت ولی به یاد داشته باشید که از ضرب دو عدد گویا، یک عدد موهومی یا گنگ حاصل نمیشود.
منظور از عبارت مزدوج چیست ؟
در مثال قبل دیدیم که دو عبارت به صورت رادیکالی وجود داشت که فقط در علامت جمع و تفریق با یکدیگر تفاوت داشتند. حال فرض کنید و یکبار با هم جمع و یکبار از هم تفریق شده باشند.

در این حالت، ضرب عباراتی را پیدا میکنیم که در آن این جمع و تفریق در هم ضرب شده باشند. به نظر میرسد که روند باید به مانند مثال قبل باشد، ولی یک راه حل ساده برای بدست آوردن این ضرب وجود دارد. حتما اتحاد مزدوج را به یاد دارید. در ادامه شکل اصلی این اتحاد را مینویسیم.
این بار به جای همان و به جای ، را قرار میدهیم. پس به کمک اتحاد دو جمله مزدوج به رابطه زیر خواهیم رسید.
زیرا و است.
در رابطه بالا، به اصطلاح را مزدوج میگویند. همینطور میتوان را مزدوج نامید. بنابراین مزدوج بودن یک رابطه دو طرفه است. پس اگر عبارت اول، مزدوج عبارت دوم باشد، نتیجه میگیریم که عبارت دوم نیز مزدوج عبارت اول است.
هنگامی که مزدوجها را در هم ضرب میکنیم، کاری مشابه آنچه در هنگام پخش ضرب در جمع اتفاق افتاد را اجرا کردهایم. به سادگی مشخص است که نتیجه برابر با اختلاف مربع هر دو عبارت است. برای مشخص شدن الگوی مزدوج به مثالهای زیر دقت کنید.
- عبارت مزدوج است.
- عبارت مزدوج است.
- عبارت مزدوج است.
نکته: برای ساختن مزدوج یک عبارت، کافی است علامت بین دو بخش از جملهها را معکوس کنیم. یعنی جمع را به تفریق یا تفریق را به جمع تبدیل کنیم. به این ترتیب مزدوج عبارت اولیه ساخته میشود.
مثال 24: مزدوج عبارت چیست؟
کافی است که علامت جمع را به تفاضل یا تفریق تبدیل کنیم. بنابراین مزدوج عبارت بالا خواهد بود.
مثال ۲۵: مزدوج کدام است؟
در اینجا هم دو عبارت مورد نظر و هستند. بنابراین مزدوج با تغییر علامت «-» به «+» ساخته میشود. پس مزدوج است.
تقسیم در عبارتهای رادیکالی
همانطور که میتوان بین ضرب رادیکالها و یک رادیکال حاوی ضرب رابطه برقرار کرد، میتوان بین تقسیم رادیکالها و تبدیل آنها به رادیکال تقسیم رابطهای نوشت چون تقسیم دقیقا به مانند عکس عمل ضرب است. مشخص است که برای این گونه محاسبات از رابطه زیر کمک خواهیم گرفت.
واضح است که هر دو رادیکال دارای فرجه یکسان هستند در غیر اینصورت امکان تبدیل تقسیم رادیکال به رادیکال تقسیم وجود ندارد. برای مثال فرض کنید قرار است عبارت زیر را ساده کنیم.
ابتدا تقسیم رادیکال را به رادیکال تقسیم تبدیل میکنیم.
در مثال بعدی از سمت راست رابطه گفته شده کمک میگیریم.
مثال ۲۶: برای ساده کردن اقدام کنید.
ابتدا رادیکال تقسیم را به تقسیم رادیکالها تبدیل میکنیم. در این حالت مشخص است که از سمت راست رابطه بالا به سمت چپ حرکت کردهایم.
گویا کردن مخرج کسرهای رادیکالی
در بخشهای قبل، تمام کسرهای حاوی رادیکال (یا رادیکالهای حاوی کسر) مخرجی داشتند که یا عدد گویا هستند یا در اثر سادهسازی به واحد تبدیل شده و کسر به یک عدد رادیکالی ساده تبدیل میشد. ولی اگر عبارت رادیکالی در مخرج کسر باقی بماند، بهتر است آن کسر را به صورتی درآوریم که مخرج آن گویا باشد.

گویا کردن مخرج کسرهای رادیکالی به صورتی اجرا میشود که با ضرب صورت و مخرج در یک مقدار ثابت، مخرج کسر به صورت مربع کامل درآمده و به صورت عدد گویا قابل نمایش باشد. در این حالت میگوییم، کسر را گویا کردهایم. گویا کردن کسر در دقت یا محاسبات بعدی اثری ندارد ولی این کار باعث میشود، خوانایی و انجام محاسبات بعدی سادهتر صورت گیرد. برای روشن شدن مراحل کار و شیوه گویا کردن کسرها، به ذکر چند مثال میپردازیم.
مثال 27: رادیکال را ساده کنید.
با توجه به قاعده تبدیل رادیکال تقسیم به تقسیم رادیکالها، این رادیکال را ساده میکنیم.
این مثال بسیار شبیه تمرین قبلی است، اما نتیجه ساده کردن «اشتباه» به نظر میرسد. چرا؟ زیرا مخرج حاوی یک رادیکال است. مخرج نباید حاوی رادیکال باشد وگرنه نتیجه یک کسر گویا نیست. همانطور که مشخص است، که در مخرج این کسر قرار دارد، یک عبارت رادیکالی است و در این مرحله باید این کسر را گویا کنیم.
نکته: چرا این محاسبه اشتباه به نظر میرسد؟ از آنجا که این مسئله ممکن است در سطح دبیرستان یا دبستان مطرح باشد، گویا کردن آن اهمیت دارد. ولی ممکن است در مقاطع دیگر تحصیلی (مانند تحصیلات دانشگاهی) گویا کردن کسر امری مهم تلقی نشود. از آنجایی که در این دو مقطع (دبستان و دبیرستان) کسرهای متعارفی مورد بحث است، به همین علت مخرج کسرهای رادیکالی را گویا کرده تا بتوانیم آنها را به صورت کسر متعارفی یا شبیه آن درآوریم.
برای دریافت پاسخ صحیح، باید مخرج را گویا کرده و آن را در ضرب کنیم تا به صورت مربع کامل درآید. ولی در این بین برای آنکه کسر تغییری نکند، صورت را هم در همین مقدار ضرب خواهیم کرد تا کسری برابر با کسر قبلی ایجاد کنیم.
به این ترتیب مخرج به صورت مربع کامل درآمد و با سادهسازی رادیکال، مخرج کسر گویا شد.
نکته: اگر به همان کسرهای دوره ابتدایی فکر کنیم، نمیتوانید کسرها را با یکدیگر جمع یا تفریق کنید مگر اینکه مخرج یکسانی داشته باشند. برای ایجاد این «مخرجهای مشترک»، کسرها را گویا کرده تا از قاعده جمع و تفریق به کمک مخرج مشترک بهره ببریم.
مثال ۲۸: کسر را گویا کنید.
مشخص است که برای تبدیل مخرج کسر به مربع کامل، صورت و مخرج را باید در ضرب کنیم. به این ترتیب به رابطههای زیر خواهیم رسید.
همانطور که میبینید از قاعده تبدیل ضرب رادیکالها به رادیکال ضرب استفاده کردهایم. همچنین در مخرج نیز شاهد ایجاد یک مربع کامل هستیم که در نتیجه عدد ۳ از زیر رادیکال خارج میشود. البته بهتر است بعد از اینکه کسر را گویا کردیم، باز هم به دنبال سادهسازی باشیم. به این منظور در کسر مشخص است که مقدار ۶ صورت با مقدار ۳ مخرج قابل ساده شده است. در نتیجه مقدار نهایی برای رابطه بالا به صورت زیر خواهد بود.
مثال 29: کسر را ساده کنید.
ساده سازی این کسر به معنی گویا کردن مخرج آن است. بنابراین با ضرب و تقسیم صورت و مخرج در یک مقدار سعتی میکنیم که مخرج را به صورت مربع کامل درآورده و کسر را گویا کنیم. در اقدام اول سعی میکنیم با ضرب صورت و مخرج در این کار را انجام دهیم، زیرا در مخرج مقدار وجود دارد.
متاسفانه با این عمل، نتوانستیم مخرج را گویا کنیم. بنابراین شاید بهتر باشد که صورت و مخرج کسر مذبور را در ضرب کنیم. این عملیات را در ادامه اجرا کردهایم.
با این کار نیز باز کسر به صورت مخرج گویا ظاهر نشد. به یاد دارید که ضرب یک عبارت رادیکالی در مزدوج آن، با استفاده از اتحاد مزدوج، آن را به صورت تقریق دو عبارت مربع در میآورد. شاید این کار بتواند چارهای برای حل این مسئله باشد.
به این ترتیب مخرج کسر حاصل از عملیات را به صورت گویا درآوردهایم.

مثال ۳۰: کسر را ساده کرده و به کسر گویا درآورید.
باز هم در این مثال به نظر میرسد که استفاده از ضرب کردن در مزدوج مخرج مفید باشد. واضح است که مزدوج برابر با است. پس رابطه بالا را به صورت زیر خواهیم نوشت.
همانطور که در مثالهای بالا نشان داده شد، انجام ضرب به طور جداگانه میتواند مفید باشد. سعی نکنید یک باره بیش از یک عمل را در یک حرکت انجام دهید. اطمینان حاصل کنید که پس از اتمام گویا کردن، هرگونه عمل ساده کردن کسر را به درستی انجام دادهاید تا نتیجه نهایی کامل و صحیح باشد.
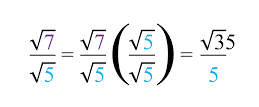
ریشهگیری مرتبههای بالاتر
عملگر جذر یا ریشه میتواند با مرتبههای بالاتر هم اجرا شود. در این حالت اصطلاحهای کعب (ریشه سوم)، ریشه چهارم و ... به کار برده میشود. ریشههای چهارم و سایر ریشههای با مرتبه بالاتر مانند ریشههای دوم ساده میشوند. اگرچه، در بعضی از حالتها، باید کمی تفکر خود را گسترش دهیم تا جواب صحیح حاصل شود. در ادامه با ذکر مثالهایی، سادهسازی رادیکالهای با درجه یا مرتبه بزرگتر از ۲ را مورد بررسی قرار خواهیم داد.
ساده سازی عبارتهای رادیکالی با مرتبه یا فرجه بزرگتر از ۲
در بخشهای قبلی، با تبدیلهای ضرب یا تقسیم رادیکال به رادیکال ضرب یا تقسیم کار سادهسازی را انجام دادیم. همچنین تجزیه به عوامل ضربی، یکی از راهکارهای مناسب برای ساده سازی عبارت های رادیکالی محسوب میشد. در اینجا هم همین عملگرها و راهکارها را برای ساده سازی عبارتهای رادیکالی با مرتبه بزرگتر از ۲ به کار خواهیم برد. برای ریشههای با مرتبه بالاتر، تفکر همان است. اگر ریشه مکعب داشته باشیم، میتوانیم هر عاملی را که به صورت توانهایی از ۳ باشند، از زیر رادیکال خارج کنیم. در ریشه چهارم، هر عاملی را که به صورت چهار ضرب یا توانی از ۴ باشد، از زیر رادیکال با فرجه ۴ خارج خواهیم کرد. در یک ریشه پنجم، هر عاملی که در زیر رادیکال به صورت توانی از ۵ نوشته شده را میتوان از زیر رادیکال خارج کرده و در پشت آن (به صورت مضرب) قرار داد. به مثالهای زیر دقت کنید.
مثال 31: عبارت را ساده کنید.
کافی است که ۱۶ را به عوامل اول خودش تجزیه کنیم.
نکته: وقتی عبارات رادیکال با فرجه زوج را ساده میکنید، (مانند ریشه ۲ یا ریشه چهارم)، باید مقدار زیر رادیکال، مثبت باشد.
مثال ۳۲: عبارت چه مقداری است؟
باز هم از تجزیه استفاده میکنیم.
مثال ۳۳: حاصل چیست؟
تجزیه ۵۴ به عوامل اول به صورت زیر صورت میگیرد.
پس به رابطه زیر خواهیم رسید.
مثال ۳۴: مقدار چقدر است؟
در این مثال هم عدد ۴۸ را به عوامل اول تجزیه میکنیم.
بنابراین حاصل رادیکال را به صورت زیر خواهیم نوشت.
مثال ۳۵: را ساده کنید.
برای حل این مسئله به شکل زیر عمل میکنیم.
مثال ۳۶: عبارت را به سادهترین عدد تبدیل کنید.
در این مثال فرض کنید که بخواهیم عدد ۲ را به داخل رادیکال ببریم. واضح است که برای ورود یک مقدار به زیر رادیکال، باید آن را درون رادیکال، به صورت توان با فرجه رادیکال بنویسیم. پس به شکل زیر عمل میکنیم.
البته این کار را به صورت دیگری نیز میتوانستیم انجام دهیم.
نکته: همیشه به یاد داشته باشید که ورود هر جمله به درون رادیکال، باعث توان رساندن آن در عبارت زیر رادیکال خواهد شد. به بیان ریاضی رابطه زیر برقرار است.

مثال 37: عبارت زیر را ساده کنید.
در این مثال، متغیرهایی زیر رادیکال وجود دارند و باید با توجه به توانهای آنها، جملههایی را از داخل رادیکال خارج کنیم. از آنجایی که فرجه رادیکال ۵ است، باید توانها را به صورت مضاربی از ۵ درآوریم. مقادیر عددی نیز در این عبارت با تجزیه به عوامل اول و تبدیل به مقادیری با توانهای ۵، قادر به خروج از زیر رادیکال هستند. به روابط زیر توجه کنید.
بنابراین سادهسازی را به صورتی که در ادامه دیده میشود، اجرا میکنیم.
بنابراین جملات با توانهای ۵ از زیر رادیکال خارج میشوند.
باز هم تاکید میکنیم که هنگام محاسبه رادیکالهایی با فرجه زوج که در زیر رادیکال، متغیر وجود دارد، شرط مثبت بودن عبارت زیر رادیکال را در نظر بگیرید. این شرط تضمیمن میکند که محاسبات به درستی صورت گرفته و نتیجه قابل اعتماد است.
ضرب رادیکال با مرتبههای بالاتر
قواعدی که برای ضرب رادیکال با فرجه ۲ یا همان ریشه دوم بیان شد برای ضرب رادیکال با مرتبههای بالاتر نیز وجود دارد. تبدیل ضرب رادیکالها با فرجه یکسان به رادیکال ضرب و همچنین تقسیم در این خصوص قابل استفاده است. این موضوع را به کمک مثالهایی که در ادامه آوردهایم، نشان خواهیم داد.
مثال 38: عبارت زیر را ساده کنید.
از آنجایی که فرجههای هر دو رادیکال یکسان هستند، میتوان آنها را در هم ضرب کرد و ضرب رادیکالها را به صورت رادیکال ضرب عبارتهای زیر رادیکال نوشت.
مثال 39: عبارت زیر را ساده کنید.
باز هم با توجه به یکسان بودن فرجه، ضرب امکانپذیر است.
حال عبارتهای همانند را با توجه به توانها ضرب کرده و نتیجه را ساده میکنیم. واضح است که جملهها با توان ۴ از زیر رادیکال خارج میشوند.
جمع و تفریق برای رادیکال با فرجه بزرگتر از ۲
جملههایی در یک عبارت رادیکالی قابل جمع کردن هستند که فرجهها و مقادیر زیر رادیکال یکسانی داشته باشند و فقط ضرایب این رادیکالها با یکدیگر تفاوت داشته باشند. این قاعده را برای رادیکال با فرجه ۲ نیز به کار بردیم. به مثالهایی در این زمینه توجه کنید.
مثال ۴۰: عبارت زیر را ساده کنید.
هر دو رادیکال با فرجه ۳ هستند ولی عبارت زیر رادیکال یکسان نیست. ولی شاید سادهسازی رادیکالها آنها را به جملات مشابه تبدیل کند.
مثال 41: عبارت زیر را ساده کنید.
در اینجا هم به مانند مقال قبل هر دو رادیکال با فرجه ۳ هستند ولی عبارت زیر رادیکال یکسان نیست. پس رادیکالها را ساده خواهیم کرد.
تقسیم رادیکال با فرجه بزرگتر از ۲
همانطور که قواعد ضرب رادیکالها را فراگرفتید، قواعد تقسیم را هم میتوانید به کار برید. به مثالهای زیر توجه کنید.

مثال 42: عبارت را ساده کنید.
با توجه به تجزیه و قاعده تبدیل رادیکال تقسیم به تقسیم رادیکال، عمل میکنیم.
مثال ۴3: عبارت را ساده کنید.
متاسفانه، مخرج این کسر گویا نیست و باید با روش گویا کردن، کسر را به صورت دیگری درآوریم.
مشخص است که صورت و مخرج را در مخرج کسر، ضرب کردهایم. نتیجه به صورت زیر خواهد بود.
نکات دیگر در مورد رادیکال
هنگام کار با رادیکالها، یاد گرفتیم که چگونه مخرج کسر را در صورت امکان به صورت گویا درآوریم اگر مخرج کسری حاوی یک مقدار رادیکالی باشد، خواندیم که میتوانیم از فرمول یا اتحاد مزدوج (یا عکس آن) برای خلاص شدن از رادیکالها استفاده کنیم. به طور خاص، یاد گرفتیم که اگر کسری را در صورت و مخرج، در یک مقدار ثابت ضرب کنیم، تغییری در آن بوجود نمیآید. از این ویژگی استفاده کرده و کسرهای رادیکالی را به شکلی درآوردیم که مخرج آنها گویا باشد. در ادامه این متن، چند مثال دیگر از گویا سازی را برای حالتهایی با رادیکال فرجههای بزرگتر از ۲ بازگو میکنیم.
مثال 44: کسر را گویا کنید.
از آنجایی که اینجا با کعب (یا ریشه سوم) یک عدد سروکار داریم، اتحاد مزدوج کارساز نخواهد بود. به رابطه زیر دقت کنید.
مشخص است که با این راه حل، مخرج کسر تبدیل به عدد صحیح یا گویا نمیشود. ولی استفاده از اتحاد مکعب مناسب به نظر میرسد. برای یادآوری اتحاد مکعب را در ادامه معرفی میکنیم.
در مثال ما، اگر و باشد، کافی است صورت و مخرج را در سمت راست تساوی بالا ضرب کنیم.
طبیعتاً، اگر علامت مخرج اصلی «منفی» بود، فرمول «اختلاف مکعب» را برای گویا سازی استفاده میکردیم. این اتحاد در رابطه زیر دیده میشود.
همانطور که دیدید، امکان تبدیل رادیکال به توان نیز برای گویا سازی یا محاسبات نظیر آن، قابل استفاده است. مشخص است که ریشه دوم به صورت یک عبارت توانی با نمای تبدیل میشود. ریشه مکعب هم به صورت یک توان به شکل ظاهر خواهد شد. همینطور، ریشه چهارم یک توان به شکل خواهد بود. این فرآیند تبدیل ریشه به توان معکوس، به محاسبات بعدی رادیکال کمک بسیاری میکند و باعث میشود، اعداد رادیکالی را به صورت اعداد تواندار تصور کرده و با همان مبنای اعداد تواندار با آنها رفتار کنیم. به این ترتیب، جمع، تفریق، ضرب و تقسیم اعداد رادیکالی درست به صورت اعداد تواندار خواهد بود. به مثالهایی که در ادامه آورده شده دقت کنید تا استفاده از این قوانین را بهتر درک کنید.
مثال 45: حاصل ضرب در را به صورت یک عبارت رادیکالی بنویسید.
با تبدیل رادیکال به حالت توانی میتوانیم، محاسبات را به راحتی انجام دهیم.

مثال ۴۶: عبارت زیر را ساده کنید.
صورت این کسر به صورت کعب و مخرج ریشه دوم است. ولی چون مقادیر زیر رادیکالها یکسان است، تبدیل آنها به صورت توانی و سادهسازی میسر خواهد بود. پس به صورت زیر عمل خواهیم کرد.
حالا دوباره توانها را به صورت رادیکال خواهیم نوشت و نتیجه را گویا خواهیم کرد.
چون توان زیر رادیکال در بخش صورت کسر، کوچکتر از فرجه رادیکال است، نمیتوان رادیکال را سادهتر کرد.
خلاصه و جمعبندی
همانطور که خواندید، جذرگیری به کمک عملیات خاصی صورت میگیرد که وابسته به تقسیم یا به توان رساندن است. در حقیقت جذر یا فرمول رادیکال را معکوس توانرساندن میدانیم. به همین جهت، همان عملیاتی که برای توان رساندن (مثل ضرب) انجام میدهیم را برای جذر یا رادیکال (مثل تقسیم) تکرار میکنیم. عملگر رادیکال و خصوصیات محاسباتی آن نیز از مواردی بود که در این مطلب به آن پرداخته شد. استفاده از اتحادهای جبری مانند اتحاد مزدوج و گویا کردن کسرهای رادیکالی از مواردی بود که در این مطلب از مجله فرادرس به آنها اشاره کرده و با ذکر مثالهای متعدد، درک آنها را تسهیل کردیم. البته در موارد دیگر مانند زمانی که فرجه رادیکال بزرگتر از ۲ بود، ابتکاراتی مانند ضرب صورت و مخرج در عبارتهایی متناسب با اتحادهای ریاضی به کار بردیم تا کسرها را گویا کنیم. مبنای مباحث به کار رفته در این متن، ساده کردن و اجرای عملیات جبری روی اعداد و همچنین عبارتهای رادیکالی بود.













10ضرب در رادیکال nمساوی ۳۷/۲۴شده مقدار nچگونه محاسبه میشه؟
سلام وقت بخیر از مطالب خوبتون ممنونم
میشه جواب این سوال رو برای من توصیح بدین ؟
ساده شده ی عبارت (رادیکال a به توان n )به صورت جبری
بازم ممنون
با سلام و خسته نباشید
عبارت های ریاضی شما در کروم به صورت 22=4 نشان داده می شه اما در Microsoft Edge درست نمایش داده می شه
سلام، وقت شما بخیر؛
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم، احتمالاً در این مورد خاص صفحه به درستی برای شما بارگذاری نشده است. لطفاً یکبار صفحه را با ترکیب کلیدهای CTRL+Shift+R رفرش کنید و کمی صبور باشید تا عبارات به درستی برای شما بارگذاری شوند بعد از آن در دیدن این موارد در مرورگر کروم نباید مشکلی داشته باشید.
سلام . خسته نباشید . اعشار رادیکال 13 به طور صحیح وارد نشده . رقم بعد از ممیز 60 است .
سلام. همه توضیحات عالی.فقط یک سوال در مثال آخر در مرحله آخر ساده سازی ۵ به توان ۶ از کجا اوند؟؟؟
سلام.
عدد مورد نظر اصلاح شد.
از همراهی و بازخورد شما سپاسگزاریم.
در مثال ۲۳ اگر رادیکال ۳۰ را به صورت ضرب رادیکال ۱۵ در رادیکال ۲ در نظر بگیریم ساده سازی می شود. بنابراین جواب نهایی ساده سازی میشه: منفی چهار رادیکال دو به علاوه ۳
سایت بسیار خوبی داشتید اما نتونستم کامل بخونم چون مِنو تون روی متن بود و روی سایت قبلی تون هم همین مشکل رو داشتم لطفا اصلاح کنید ?
سلام بسیار عالی بود منتهی نتونستم جواب سوالم و پیدا کنم عبارت رادیکال nضربه در رادیکال n+1 منهای رادیکال n
لطفا راهنمایی کنین
سلام، وقت شما بخیر؛
اگر راهنمایی بفرمائید که روی چه دستگاهی وبسایت را با این مشکل مشاهده میکنید، از چه سیستم عامل و چه مرورگری بهره میگیرید، حتما تلاش خواهیم کرد این موضوع را بررسی و در اسرع وقت رفع کنیم.
از اینکه با مجله فرادرس همراه هستید و با ارائه بازخود ما را در بهتر شدن یاری میکنید، بسیار سپاسگزاریم.