خرپا چیست؟ — به زبان ساده

در مطالب گذشته در مورد مفاهیم بنیادین استاتیک بحث شد. همچنین در مطلبی جداگانه مثالهایی از استاتیک را بیان کردیم. در این مطلب قصد داریم تا در مورد کاربرد مفاهیم استاتیک در یکی از مهمترین بخشهای سازهها یعنی خرپا بحث کنیم.
خرپا چیست؟
خرپا سازهای چند عضوی است که تمامی بخشهای آن به یکدیگر پین شدهاند. معنی پین این است که در هیچ مفصلی گشتاوری وجود ندارد؛ بنابراین در خرپا فقط نیرو وجود دارد.
در شکل زیر میتوانید یک خرپا و نیروهای خارجی وارد شده به آن را ببینید.
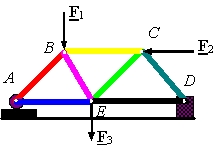
روشهای تحلیل نیرو در خرپا
در حالت کلی بهمنظور تحلیل نیروهای موجود در یک خرپا از دو روش «مفاصل» (Joints) و «مقاطع» (Sections) استفاده میشود. در هر خرپا با اعمال نیروی خارجی، درون هر عضو نیرویی ایجاد خواهد شد.
برای مثال در خرپای شکل بالا که دو نیروی F۲ ،F۱ و F3 به آن وارد میشود، نیروهایی مطابق شکل زیر، در آن ایجاد شده است.
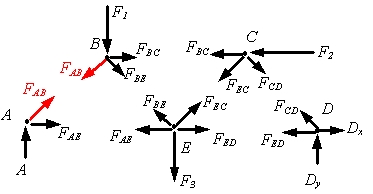
روش مفاصل
در این روش هر مفصل را به صورت تنها تصور کنید؛ سپس برآیند تمامی نیروهای وارد شده به آن را صفر قرار دهید. بنابراین به منظور تحلیل نیرویی خرپا با استفاده از روش مفاصل، به ترتیب زیر عمل کنید:
- هر مفصل را به صورت جدا تصور کنید.
- نیروهای وارد شده به مفصل را معین کنید.
- برآیند نیروهای رسم شده روی مفصل را در راستای x و y برابر با صفر قرار دهید.
برای درک بهتر این روش، به مثالهای ارائه شده در انتهای این مطلب مراجعه فرمایید.
روش مقاطع
در این روش بخشی از خرپا جدا شده و به عنوان سیستم در نظر گرفته میشود. سپس برآیند نیروها و گشتاورهای وارد شده به آن برابر با صفر قرار داده شده و نیروهای مجهول در مسئله بدست میآیند. بنابراین برای بدست آوردن نیروهای مجهول موجود در یک خرپا به ترتیب زیر عمل کنید:
- انتخاب بخشی مناسب از خرپا به عنوان سیستم (این مفهوم در مثالهای ارائه شده در پایین، به شکلی دقیقتر توضیح داده شده)
- قرار دادن تمامی نیروهای - خارجی - وارد شده به سیستم انتخاب شده
- نوشتن معادله تعادل گشتاور و نیرو برای سیستم مفروض و محاسبه نیروهای مجهول قرار گرفته روی آن
نکات کاربردی و مهم در تحلیل نیرویی خرپا
توجه داشته باشید که همواره در تحلیل نیرویی خرپا، روشهایی میانبر وجود خواهند داشت. از این رو در این قسمت نکاتی مهم در مورد تحلیل نیرویی یک خرپا، در زمان کمتر را ارائه خواهیم داد.
۱. اعضای خنثی در خرپا
در یک خرپا ممکن است اعضایی وجود داشته باشند که نیرویی را حمل نکنند. این جمله به این معنی است که در عضو مد نظر نیرویی وجود ندارد. در حقیقت میتوان خرپا را بدون آن عضو تصور کرد. برای مثال در شکل زیر اعضایی که به رنگ آبی، قرمز و صورتی مشخص شدهاند، نیرویی را در خود حس نمیکنند. [میتوان تصور کرد که این اعضا در خرپا وجود ندارند.]

اجازه دهید مفهوم عضو خنثی را دقیقتر توضیح دهیم. در شکل بالا عضو B را بیرون کشیده و نیروهای وارد شده به مفصل را روی آن قرار میدهیم. در شکل زیر این کار انجام شده.
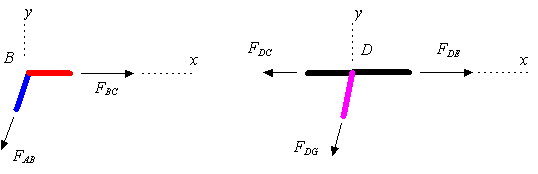
طبق مفاهیم بیان شده در مطلب مفاهیم استاتیک، بایستی برآیند نیروهای وارد شده به مفصل، در هر دو راستای x و y صفر باشد. بنابراین معادله تعادل نیرویی در راستای y برای این مفصل را میتوان به صورت زیر نوشت.
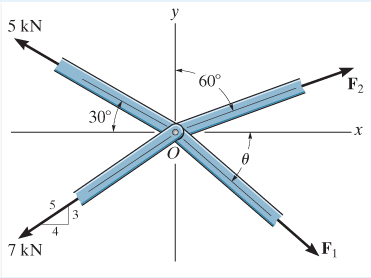
۲. نیروهای دو عضوی که در یک راستا قرار گرفتهاند
یک مفصل در خرپا ممکن است به شکلی قرار گیرد که فقط نیرو را از عضوی به عضو مقابل خود انتقال دهد. برای مثال در شکل زیر هیچ تغییری در نیروهای اطراف مفصل اتفاق نمیافتد و فقط نیرو در دو عضوی که در مقابل هم قرار دارند، منتقل میشود. برای نمونه در این خرپا روابط F1=F3 و F4=F2 برقرار هستند.
در حقیقت در چنین مفاصلی، تمامی نیروهای قرار گرفته در یک راستا، اندازه برابری دارند.
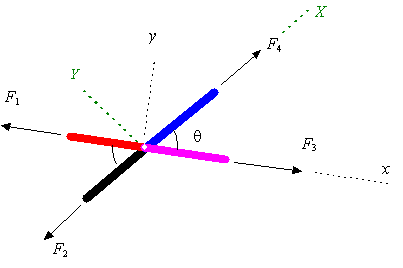
مثلا در این مفصل نیروهای F1 و F3 در راستای X قرار گرفتهاند و به همین دلیل با هم برابر هستند.
۳. خرپای معین و نامعین
توجه داشته باشید که همواره به منظور تحلیل یک خرپا بایستی تعداد معادلات و تعداد نیروها با یکدیگر برابر باشند. برای بررسی این موضوع اجازه دهید چند نمونه را بررسی کنیم. شکل زیر را در نظر بگیرید. میخواهیم تعداد نیروهای مجهول در این سازه و تعداد معادلاتی که میتوان برای آن نوشت را مورد بررسی قرار دهیم. به نظر شما برای تحلیل این خرپا، چند نیروی مجهول وجود دارد.

نیروهای مجهول در شکل خرپای بالا:
در حقیقت هر عضو یک نیرو را شامل میشود و ۳ عکس العمل تکیه گاه در A و D [یک نیرو در A و دو نیرو در D] وجود دارند. بنابراین کلا ۱۰ نیرو بایستی محاسبه شود. همچنین این خرپا از ۵ مفصل تشکیل شده که در هرکدام از آنها میتوان ۲ معادله تعادل نیرویی، در راستای x و y نوشت. در نتیجه میتوان ۱۰ معادله تعادل نیرویی، برای خرپا نوشت. به طور خلاصه میتوان گفت: ۱۰ مجهول و ۱۰ معادله برای این خرپا وجود دارد. به چنین سازههایی، معین گفته میشود.
حال میخواهیم شما را به چالش بکشیم. بدین منظور خرپای زیر را در نظر بگیرید. به نظر شما در این خرپا چند نیرو وجود دارد؟ همچنین چند معادله میتوان نوشت؟

نیروهای مجهول در این خرپا عبارتند از:
بنابراین ۹ نیروی مجهول در این خرپا وجود دارد. همچنین معادلاتی را که میتوان برای این خرپا نوشت به شرح زیر هستند.
این خرپا از ۴ مفصل تشکیل شده که بررای هرکدام از آنها میتوان دو معادله تعادلی و را نوشت. بنابراین ۸=۲×۴ معادله میتوان برای این خرپا نوشت.
در نتیجه این خرپا دارای ۹ مجهول است؛ در حالی که میتوان ۸ معادله برای آن نوشت. به خرپایی که تعداد معادلات آن از تعداد نیروهای مجهولش کمتر باشد، خرپای نامعین گفته میشود.
به منظور تحلیل نیرویی خرپای بالا، یکی از عضوهای AC یا BD بایستی حذف شود [با این کار یک مجهول از معادلات کنار رفته و تعداد مجهولات و معادلات با هم برابر میشود].
۴. مکانیزم
در بالا به این نکته اشاره کردیم که اگر تعداد مجهولات در یک خرپا بیشتر از معادلاتش باشد، به آن نامعین گفته میشود و به منظور تحلیل نیرویی، بایستی یکی از عضوهای خرپا را حذف کرد. حال شرایطی برعکس را تصور کنید. یعنی فرض کنید که در یک خرپا تعداد معادلات، از تعداد مجهولات بیشتر باشد. برای نمونه شکل زیر را تصور کنید.
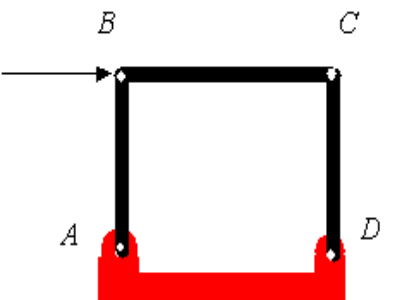
نیروهای مجهول در این سازه عبارتند از:
بنابراین این سازه دارای ۷ نیروی مجهول است.
از طرفی این سازه دارای ۴ مفصل است که برای هر کدام از آنها میتوان دو معادله تعادل، در راستای x و y نوشت؛ در نتیجه ۸=2×۴ معادله قابل بیان هستند. بنابراین این سازه دارای ۸ معادله و ۷ مجهول است. جالب است چرا که تعداد معادلات از تعداد مجهولات بیشتر شده.
به سازهای که در آن تعداد معادلات نیرویی از تعداد نیروهای مجهول بیشتر باشد، مکانیزم گفته میشود. چنین سازهای قابلیت تحمل بارگذاری را نداشته و میتواند با گذشت زمان تغییر شکل دهد.
انیمیشن زیر نشان میدهد که چگونه این خرپا ناپایدار بوده و با اعمال نیرو به حرکت در میآید.
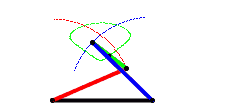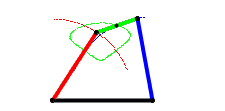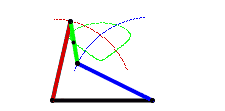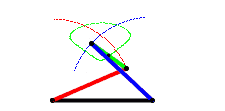
مثالها
پس از بیان نکات و مفاهیم بدست آوردن نیروهای موجود در یک خرپا، حال وقت آن رسیده که از این مفاهیم در مسائل کاربردی استفاده کنیم.
مثال ۱
با استفاده از روش مفاصل، نیروهای موجود در خرپای زیر را بیابید.
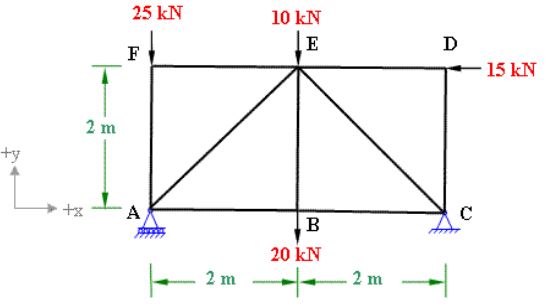
اگر به شکل دقت کنید، قسمت A به صورت غلتک و نقطه C به عنوان مفصل در نظر گرفته میشود. از این رو بایستی توجه داشته باشید که نیرویی در راستای y، در مفصل A وجود ندارد. برای حل این مسئله به صورت زیر عمل کنید.
قدم اول: تعیین تعداد معادلات و مجهولات در این خرپا
همانطور که در شکل نیز میبینید، این خرپا از ۹ عضو تشکیل شده [AF, AB, AE, BE, BC, CE, CD, DE, EF]. بنابراین ۹ نیروی مجهول در اعضا این خرپا وجود دارد. همچنین در نقطه C دو نیروی عکس العمل Cx و Cy به خرپا وارد میشود. توجه داشته باشید به علت این که مفصل A به صورت غلتک است، نیرویی در راستای x در A وجود ندارد. بنابراین کل نیروهای مجهول در خرپا برابر با ۱۲=۹+۲+۱ است.
برای بدست آوردن تعداد معادلات نیرویی که میتوان برای این خرپا نوشت، بایستی تعداد مفاصل را محاسبه کرد. در این مسئله، ۶ مفصل وجود دارد. با نوشتن تعادل نیرویی در راستاهای x و y برای هر کدام از آنها، به ۱۲ معادله میرسیم.
قدم دوم: محاسبه نیروهای عکس العمل در تکیهگاه
با در نظر گرفتن کل خرپا به عنوان سیستم، نیروهای زیر به آن وارد میشود.
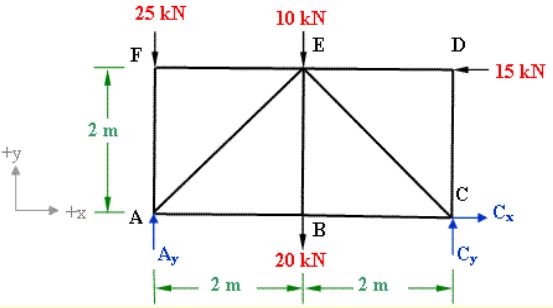
با نوشتن تعادل نیرو در راستای x میتوان نیروی را به صورت زیر محاسبه کرد.
بر همین مبنا میتوان معادله تعادل نیرویی در راستای y را به شکل زیر نوشت.
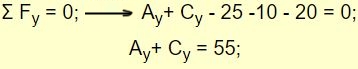
از آنجایی که سیستم ساکن است، بنابراین گشتاور خالصی نیز به آن وارد نمیشود. در نتیجه با صفر قرار گشتاور حول نقطه A داریم:
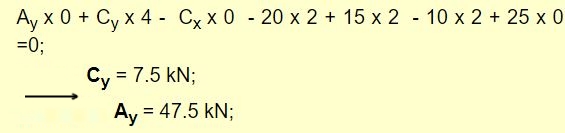
قدم سوم: محاسبه نیروی موجود در اعضاء خرپا
در این مرحله با استفاده از روش مفاصل، نیروهای موجود در اعضاء خرپا را محاسبه میکنیم. بدین منظور در ابتدا به اعضایی نگاه کنید که بیشتر از ۲ نیروی مجهول نداشته باشند. در این مسئله دو مفصلِ D و F، دارای دو نیروی مجهول هستند. در نتیجه مفصل D را انتخاب میکنیم. توجه داشته باشید که نیروی موجود در یک عضو، همواره به صورت کششی یا فشاری است. در شکل زیر نیروهای کششی و فشاری برای یک مفصل فرضی، نشان داده شدهاند.

از آنجایی که نیروها مجهول هستند و نمیدانیم که کدامیک کششی و کدامیک فشاری است، در ابتدا همه نیروهای موجود در اعضا را به صورت کششی فرض میکنیم؛ پس از آنکه نیروها محاسبه شدند، علامت مثبت به معنای کششی بودن آنها است و علامت منفی به معنای فشاری بودن. معادل تعادل نیروها در راستای x و در نقطه D را به شکل زیر مینویسیم:
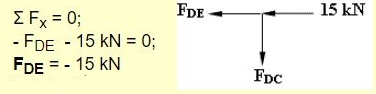
علامت منفی مقابل نیروی FDE نشان میدهد که نوع آن فشاری است. قبل از اینکه تعادل نیروها در راستای y را بنویسیم، به نظر شما مقدار نیروی F چقدر است؟ بهغیر از این نیرو هیچ نیروی دیگری در این راستا وجود ندارد، بنابراین برای تعادل نقطه D در راستای y، نیروی FDC بایستی صفر باشد. برای اطمینان از این نتیجه، تعادل نیروها در راستای y را به شکل زیر مینویسیم:
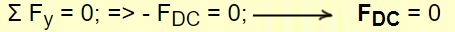
از طرفی معادله تعادل نیرویی در دو راستای x و y، برای نقطه F را میتوان به شکل زیر بیان کرد:
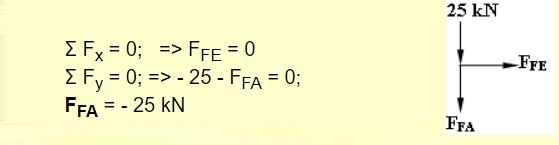
توجه داشته باشید که نیروی FFA دارای علامت منفی است، بنابراین این نیرو نیز بایستی به صورت فشاری در نظر گرفته شود [فقط جهت آن را برای محاسباتی که در ادامه انجام میدهید به صورت عکس فرض کنید].
با بدست آمدن این نیروها دوباره به سیستم نگاه کنید و به دنبال مفاصلی بگردید که فقط دو نیروی مجهول در آنها باشند. در این مرحله از حل، مفاصل A و C دارای دو نیروی مجهول هستند. همانطور که در شکلِ خرپای این مسئله نیز میبینید، ممکن است بعضی از نیروهای مفصلی به صورت کاملا افقی یا عمودی نبوده و با محورهای مختصات زاویه داشته باشند. در این شرایط در ابتدا بایستی آنها را در راستای محورها، تجزیه کرد و سپس معادله تعادل نیرویی را نوشت. برای نمونه زاویه نیروی FAE با جهت مثبت محور x برابر با ۴۵ درجه است؛ از این رو معادله تعادل نیرویی برای مفصل A را میتوان به شکل زیر بیان کرد:
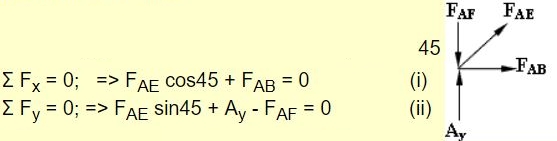
با قرار دادن نیروهای Ay و FAF در معادله ii به رابطه زیر میرسیم.
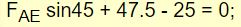
بنابراین نیروی FAE برابر با ۳۱.۸۲- بدست میآید. از این رو این نیرو نیز به صورت فشاری است. با جایگذاری این مقدار در رابطه i میتوان نیروی FAB را بدست آورد.
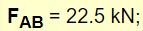
حال میتوان معادله تعادل را حول نقطه C به صورت زیر بیان کرد:
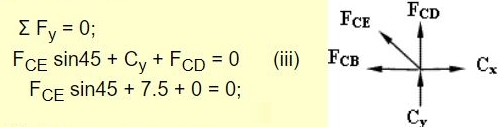
از این معادله، نیروی FCE برابر با ۱۰.۶۱- محاسبه میشود.
برای مفصل C معادله تعادل نیرویی در راستای x را میتوان به شکل زیر نوشت:

با جایگذاری FCE در معادله (iv) داریم:
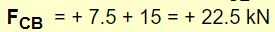
به همین شکل و با نوشتن تعادل نیرویی برای مفصل B، میتوان نیروی BE را نیز به صورت زیر محاسبه کرد.
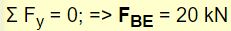
همانطور که دیدید، تمامی نیروهای موجود در این خرپا محاسبه شدند. در جدول زیر اندازه و نوع این نیروها بیان شده است.
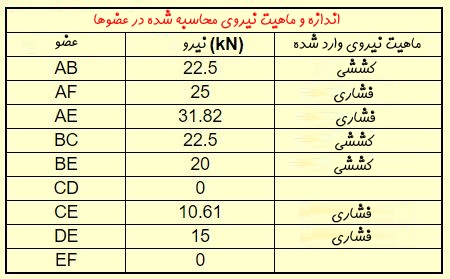
همانطور که دیدید مسئله با استفاده از روش مفاصل حل شد. توجه داشته باشید که در حل مسائل استاتیکی اینکه در ابتدا نیروی کدام عضو محاسبه شوند، بسیار مهم است. در حقیقت یک مسئله استاتیکی را میتوان به چندین روش حل کرد؛ اما نکته اینجا است که یک روش ممکن است ۱۵ دقیقه زمان ببرد و روش دیگر ۱ ساعت و ۱۵ دقیقه!
در ادامه به مثالی در مورد روش مقاطع خواهیم پرداخت. توجه داشته باشید که این روش، به نسبت زمان کمتری برای حل نیاز دارد؛ از این رو سعی کنید در مواجه با مسائل استاتیک، تریجیحاً از این روش نیز استفاده کنید.
مثال ۲
با استفاده از روش مقاطع، نیروی عضوهای BC، CE و EF را در خرپای زیر را محاسبه کنید.
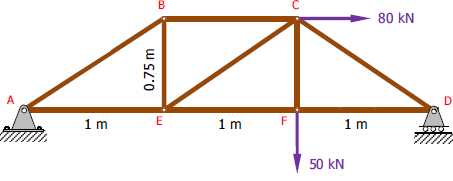
همانطور که در مثال قبل نیز اشاره کردیم، در ابتدا بایستی تعداد معادلات و نیروهای مجهولِ خرپا را یافت. این سازه دارای ۶ مفصل، بنابراین ۱۲ معادله خواهد بود. همچنین این خرپا دارای ۹ عضو و سه عکس العمل تکیهگاهی است؛ در نتیجه ۱۲ نیروی مجهول نیز در این خرپا خواهیم داشت.
همانطور که در مثال ۱ نیز بیان کردیم قدم دوم این است که عکسالعملهای تکیهگاهی را بیابیم. از این رو راحتتر آن است که معادله تعادل گشتاور را حول نقطه A بنویسیم. نقطه A به این دلیل انتخاب شده چون با نوشتن گشتاور حول آن، دو نیروی مجهول AX و Ay در معادله ظاهر نخواهند شد. بنابراین گشتاور حول مفصل A را میتوان به شکل زیر بیان کرد:
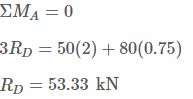
در نتیجه نیروی عکسالعمل، در مفصل غلتکی D بدست آمد.
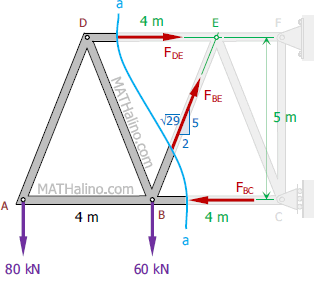
قدم دوم این است که بخشی از خرپا را به عنوان سیستم انتخاب کنیم. در روش مقاطع این قدم بسیار مهم است. گاهی با انتخاب یک مقطع مناسب میتوانید زمان حل مسئله را بسیار کوتاه کنید. مطابق با شکل زیر، در راستای b-b خرپا را به دو بخش تقسیمبندی میکنیم.
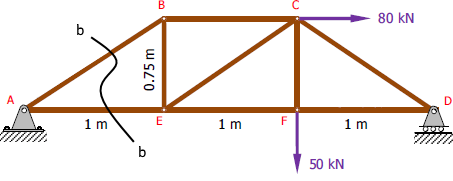
بخشِ سمت راستِ مقطع b-b را به عنوان سیستم در نظر میگیریم. در این حال با نوشتن معادله تعادل گشتاور حول نقطه E میتوان نیروی FBC را محاسبه کرد. بنابراین داریم:

با استفاده از همین روش و بهمنظور محاسبه نیروی FEF، میتوان خرپا را در مقطع a-a برش زد و سمت راست آن را به عنوان سیستم در نظر گرفت. در این حالت با نوشتن معادله تعادل حول نقطه C میتوان نیروی FEF را به شکل زیر محاسبه کرد.

نهایتا با استفاده از نوشتن تعادل نیروی در راستای y قادریم تا نیروی FCE را محاسبه کنیم. بنابراین نیروی مذکور به صورت زیر بدست خواهد آمد.

همانطور که دیدید در این روش نیز همانند روش مفاصل در ابتدا بایستی عکس العملهای تکیهگاه را یافت و پس از آن به ادامه حل پرداخت.
مثال ۳
کدام یک از عضوهای خرپای زیر خنثی هستند.
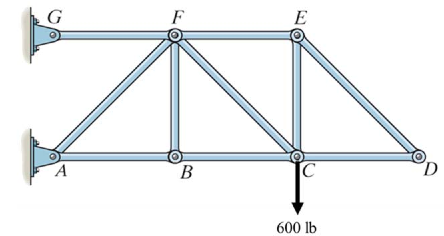
همانطور که اشاره شد، در بعضی از مسائل عضوهایی در سیستم وجود دارند که نیرویی در آنها نیست. بنابراین شناسایی این عضوها در ابتدای حل، بسیار کمک کننده خواهد بود.
مفصلی را تصور کنید که تنها دو عضو به آن متصل شده است. اگر هیچ نیرویی به مفصل مفروض وارد نشود، هر دو عضو خنثی خواهند بود [در بالا بیان کردیم که عضو خنثی به این معنا است که نیرویی در آن وجود نداشته باشد].
مفصل D در شکل بالا را در نظر بگیرید. این مفصل دو عضوی است و همچنین نیرویی به آن وارد نمیشود، بنابراین نیروی دو عضو ED و CD برابر با صفر هستند. از این رو شکل بالا را میتوان به صورت زیر تصور کرد.
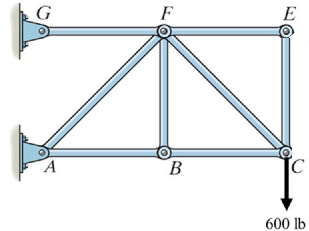
بنابراین توانستیم با شناسایی اعضای صفر نیرویی، مسئله را آسانتر کنیم. حال به نظر شما در شکل بالا عضو صفر نیرویی وجود دارد؟ همانطور که در شکل بالا میبینید مفصل E به دو عضو متصل شده و نیرویی به آن وارد نمیشود. بنابراین عضوهای EF و CE صفر نیرویی بوده و میتوان آنها را در تحلیل نیرویی، جزء خرپا حساب نکرد. بنابراین شکل اولیه را همچنان میتوان سادهتر کرد. نهایتا قادریم تا سیستم نهایی را به صورت زیر تصور کنیم.
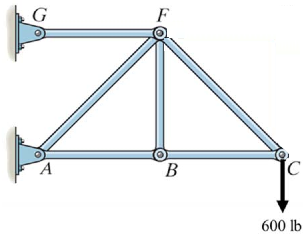
بنابراین از منظر تحلیل نیرویی سه خرپای زیر معادل هم هستند که در آن نیز برابر با صفر است.
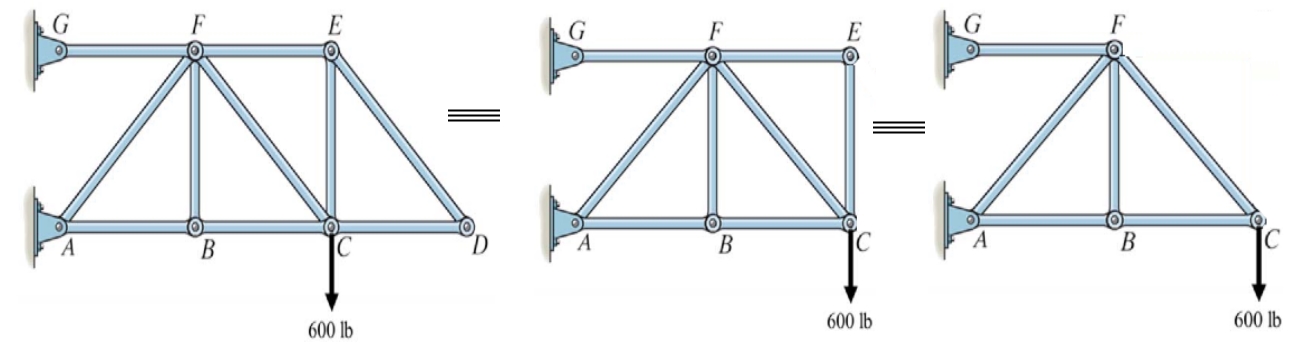
^^













در توضیحات گفته شده که اتصلات خرپا بصورت پین (مفصل) باهم در اتصال هستند. ولی در حالت کاربردی اتصلات اکثر خرپاها بصورت جوشکاری متصل شده اند. آیا آنها خرپا محسوب نمی گردند؟
با تشکر
با سلام
لطفا در خصوص اعضای صفر نیرویی در خرپاها توضیحات کاملتری بیان کنید.
با تشکر
تصویر اخر باز هم امکان ساده تر شدن داره
FB هم عضو خنثی هست
ممنون ولی در مثال آخر نیروی عضو FB هم برابر صفر است. (با در نظر گرفتن تعادل نقطه مادی در مفصل B)
سلام، وقت شما بخیر؛
بله، این موضوع به مطلب اضافه شد.
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.
بسیار دقیق و خلاصه
ممنون از لطفتون
با تشکر، بسیار مفید و توضیحات کامل و جامع بود، بیش از پیش موفق باشید
سلام لطفا یه مطلب هم راجع به قاب چیست بذارید. من سرچ کردم
تو سایت چیزی پیدا نکردم. با تشکر
عاااااااااااالی بود
بسیار بسیار میفید و عالی
واقعا ممنون از توضیح بسیار خوبتون
عالی
خدا خیرت بدهه
سلام ببخشید نیروی. افقی تو خرپاهایی مثل پرت با دو پایه مفصل چطور محاسبه میشه؟
باورتون نمیشه الان فهمیدم داستان چیه یه دنیا ممنون. خیلی خوبه که قدم به قدم با مثال توضیح دادین
عاااااااااااالی. خیییلی خوب بود.
آقا خدا خیرتون بده. دو ترمه دارم میفتم استاتیک رو. جناب عوض زاده امکانش هست باهاتون هماهنگ کنم برای کلاس خصوصی هزینشم هم مهم نیس هر چه قدر بگین اوکی هستش.