محاسبه حجم مخروط و فرمول آن – با مثال و حل تمرین

اگر به اطراف خود دقیقتر نگاه کنیم، شکلهای هندسی مختلفی از جمله مخروطها وجود دارند که با مطالعه ریاضیات و هندسه، میتوانیم ویژگیهای مختلف این شکلها را یاد بگیریم. در این مطلب از مجله فرادرس قصد داریم شما را با حجم مخروط آشنا کنیم. ابتدا توضیح میدهیم که مخروط چیست، سپس فرمول حجم مخروط، انواع مخروط و نحوه محاسبه حجم مخروط را بیان میکنیم. در انتها با حل مثالها و تمرینهای مختلف، به شما کمک میکنیم تا در مورد حجم مخروط و نکات آن، یادگیری کاملی بهدست آورید.
حجم مخروط چیست؟
حجم مخروط فضایی است که توسط یک مخروط در سه بعد اشغال میشود و فرمول آن برابر است با یک سوم حاصلضرب مساحت قاعده مخروط در ارتفاع آن. به عبارت دیگر، اگر شعاع قاعده مخروط r و ارتفاع آن h باشد، حجم مخروط برابر است با . مخروط یک شکل هندسی سه بعدی است که از دو بخش به نام قاعده و سطح جانبی تشکیل شده است. قاعده مخروط، یک دایره است و سطح جانبی آن که روی قاعده قرار میگیرد، در نقطهای به نام راس مخروط باریک میشود.
مقدار حجم مخروط یا هر شکل هندسی دیگری در قالب مکعب یا توان سوم واحدهای اندازهگیری بیان میشود. برای مثال حجم یک ظرف مخروطی شکل مانند یک قیف، بهصورت ۱۰۰ cm۳ یا ۱ m۳ بیان میشود.
مخروط چیست؟
نان بستنی قیفی، کلاه تولد و مخروطهای ترافیکی قرمز رنگ ورود ممنوع در خیابانها، مثالهای واضحی از اجسام مخروطی شکل اطراف ما هستند. مخروط یک شکل هندسی سه بعدی است که از چرخاندن یک مثلث حول هر کدام از راسهایش تشکیل میشود. هر مخروط دارای دو بخش اساسی است:
- سطح مقطع مخروط: سطح دایرهای شکل تخت و همواری که به آن «قاعده» (Base) هم گفته میشود.
- سطح جانبی مخروط: سطح منحنی شکلی که روی قاعده قرار میگیرد و در نقطهای به نام «راس مخروط» (Vertex) باریک میشود.

از نظر هندسی سه پارامتری که در محاسبه حجم مخروط موثر هستند، عبارتاند از:
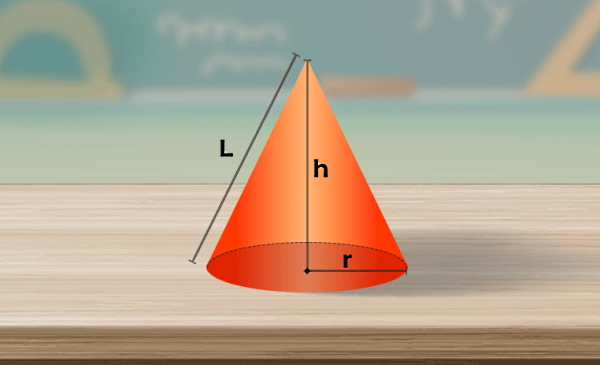
- شعاع مخروط (r): فاصله بین مرکز سطح مقطع دایرهای شکل مخروط تا هر نقطه روی محیط دایره.
- ارتفاع مخروط (h): فاصله بین راس مخروط تا مرکز سطح مقطع دایرهای شکل مخروط.
- یال مخروط (l): فاصله بین نوک مخروط تا هر نقطهای در لبه بیرونی قاعده دایرهای شکل مخروط.
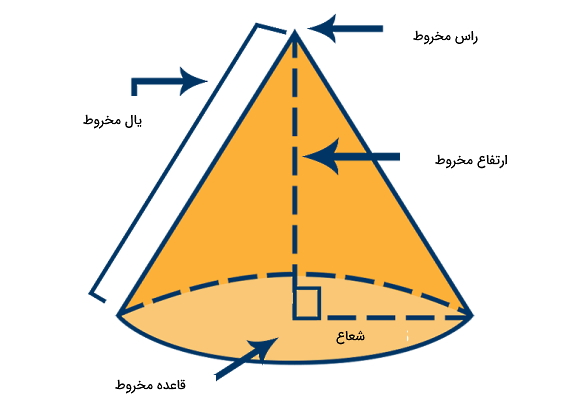
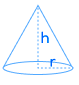
اگر بخواهیم یال مخروط را برحسب ارتفاع و شعاع آن بهدست آوریم، از قضیه فیثاغورس برای مثلثی قائمالزاویهای که با این سه پارامتر ساخته میشود، استفاده میکنیم. نتیجه برابر خواهد شد با . این سه پارامتر هندسی مهم در مخروط، در شکل زیر نمایش داده شدهاند.
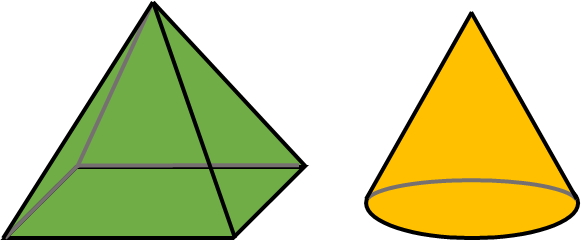
مخروط یکی از انواع «هرم» (Pyramid) محسوب میشود که دارای قاعدهای به شکل دایره است. در انواع هرمها، قاعده میتواند بهصورت چندضلعیهای مختلف باشد. بنابراین هرمها «چندوجهی» (Polyhedron) محسوب میشوند. اما مخروط بهعلت داشتن قاعده دایرهای شکل، چندوجهی نیست. در واقع هرم دارای چند وجه مثلثی شکل است که مساحت جانبی آن را تشکیل میدهند. این در حالی است که «سطح جانبی» (Lateral or Curved Surface) مخروط، یک سطح منحنی شکل و پیوسته است.
اگر بخواهیم دقیقتر با مخروط آشنا شویم، ابتدا باید یاد بگیریم که بهطور کلی مفاهیمی مانند مساحت جانبی یا حجم چه معنایی دارند. بعد از آن، به محاسبه مساحت جانبی مخروط و یافتن فرمول حجم مخروط خواهیم پرداخت.
حجم چیست؟
میدانیم مقاطع مخروطی میتوانند دو بعدی یا سه بعدی باشند. برای مثال یه برگه کاغذ تقریبا یک جسم دو بعدی محسوب میشود، در حالی که کتاب یک جسم سه بعدی است. اگر دانشآموز رشته ریاضی و فیزیک هستید، با مشاهده فیلم آموزشی هندسه ۳ – پایه دوازدهم فرادرس میتوانید یادگیری خود در مورد مقاطع مخروطی را تقویت کنید. لینک این فیلم در ادامه قرار داده شده است:
معمولا بیشتر اجسام در محیط اطراف ما سه بعدی هستند. به همین ترتیب، اشکال هندسی هم دو بعدی یا سه بعدی هستند. برای نمونه «دایره» (Circle) و «مربع» (Square) اشکال هندسی دو بعدی هستند که معادل سه بعدی آنها «کره» (Sphere) و «مکعب» (Cube) است. در دو بعد کمیت مهم «مساحت» (Area) است، در حالی که در سه بعد محاسبه حجم مهم میشود.
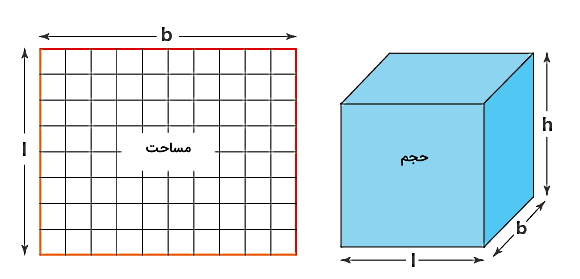
هر جسم سه بعدی فضایی را اشغال میکند که حجم نامیده میشود. بنابراین اندازه فضای اشغال شده توسط یک جسم، معادل حجم آن جسم است. برای مثال، با دانستن حجم یک بطری آب میدانیم که این بطری با چه مقدار آب کاملا پر میشود. از آنجایی که اجسام سه بعدی مختلف شکلهای مختلفی دارند، حجم آنها نیز متغیر است. برای مثال حجم کره با حجم «استوانه» (Cylinder) یا مکعب متفاوت است. در جدول زیر خلاصهای از فرمول حجم اشکال هندسی سه بعدی مختلفی که معمولا با آنها کار داریم، بیان شده است:
| فرمول حجم | پارامترهای مهم در شکل هندسی | نام شکل هندسی سه بعدی |
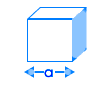 | مکعب | |
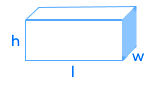 | مکعب مستطیل | |
 | کره | |
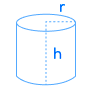 | استوانه | |
 | مخروط |
مساحت سطح جانبی چیست؟
معمولا اشکال هندسی مانند مخروط یا استوانه، دارای دو نوع سطح مختلف هستند. یک سطح، سطح تخت قاعده آنها است که مساحت آن، مساحت قاعده نام دارد. سطح دیگر، یک سطح منحنی شکلی است که روی قاعده سوار میشود. این سطح را سطح جانبی مینامند. بنابراین وقتی از مساحت سطح جانبی صحبت میکنیم، منظورمان فقط مساحت این سطح منحی شکل است نه مساحت قاعده.
در هندسه، اشکال هندسی مختلف دارای مساحت جانبی متفاوتی هستند که با فرمولهای مشخصی قابل محاسبه است. در جدول زیر، خلاصهای از فرمول مساحت جانبی اشکال هندسی مهم آورده شده است:
| فرمول مساحت سطح جانبی | پارامترهای مهم در شکل هندسی | نام شکل هندسی سه بعدی |
 | مکعب | |
 | مکعب مستطیل | |
 | کره | |
 | استوانه | |
 | مخروط با یال l |
مساحت کل چیست؟
مساحت سطح کل یک جسم سه بعدی برابر است با مساحت تمام وجوه بیرونی آن. مفهوم مساحت کل با مفهوم مساحتی که برای یک شکل هندسی دو بعدی محاسبه میکردیم، متفاوت است. یک مثال در زندگی عادی برای مفهوم مساحت کل یک شکل سه بعدی، زمانی است که میخواهیم یک هدیه با شکل نامنظم را بستهبندی کنیم. بهطور کلی، مساحت سطح کل یک شکل هندسی سه بعدی برابر است با مجموع مساحت قاعدهها و مساحت سطح جانبی آن شکل.
| فرمول مساحت سطح کل | پارامترهای مهم در شکل هندسی | نام شکل هندسی سه بعدی |
 | مکعب | |
 | مکعب مستطیل | |
 | کره | |
 | استوانه | |
 | مخروط با یال l |
در مطالب قبلی مجله فرادرس مانند مطلب «مخروط، کره و استوانه — حجم و مساحت اشکال هندسی به زبان ساده» حجم و مساحت مهمترین اشکال هندسی بهصورت خلاصه توضیح داده شده است. حالا که یاد گرفتیم تفاوت حجم، مساحت سطح جانبی و مساحت سطح کل یک شکل هندسی سه بعدی چیست، در بخشهای بعدی ابتدا فرمول مساحت جانبی مخروط را بهدست میآوریم، سپس به محاسبه حجم مخروط خواهیم پرداخت.
چگونه یادگیری حجم مخروط را با فرادرس شروع کنیم؟
تا اینجا یاد گرفتیم که مخروط چیست و با فرمولهای حجم، مساحت جانبی و مساحت کل اشکال هندسی سه بعدی مهم نیز آشنا شدیم. چنانچه دانشآموز هستید و میخواهید اطلاعات کاملتری در مورد مخروط و سایر شکلهای هندسی از طریق مشاهده فیلمهای آموزشی بهدست بیاورید، پیشنهاد میکنیم از فیلمهای تهیه شده در فرادرس استفاده کنید:
- فیلم آموزش ریاضی نهم فرادرس
- فیلم آموزش ریاضی نهم تست آزمون نمونه دولتی و تیزهوشان فرادرس
- فیلم آموزش ریاضی ۳ دوازدهم علوم تجربی فرادرس
- فیلم آموزش هندسه ۳ دوازدهم ریاضی و فیزیک فرادرس
- فیلم آموزش رایگان مثلث فرادرس
- فیلم آموزش رایگان پنج ضلعی فرادرس
- فیلم آموزش رایگان مکعب فرادرس
- فیلم آموزش رایگان هرم فرادرس
محاسبه مساحت جانبی مخروط
در این قسمت میخواهیم فرمول مساحت سطح جانبی مخروطی با شعاع r و یال l را بهدست آوریم. مطابق شکل زیر، اگر سطح جانبی این مخروط را باز کنیم، به یک «قطاع» (Sector) دایره خواهیم رسید. شعاع این قطاع برابر است با یال مخروط (l). از طرفی میدانیم محیط قاعده مخروط، محیط دایرهای به شعاع r است. پس با باز کردن سطح جانبی مخروط، اندازه کمان قطاع برابر با محیط قاعده خواهد بود. کافی است مساحت این قطاع را حساب کنیم تا مساحت سطح جانبی مخروط موردنظر بهدست آمده باشد.
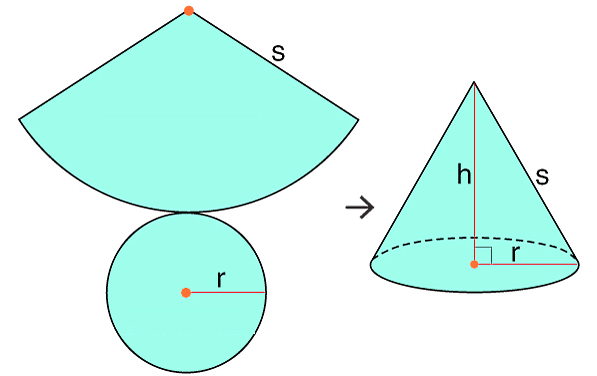
اگر بهجای قطاعی به شعاع l، یک دایره کامل به شعاع l در نظر میگرفتیم، محیط آن میشد. در این قسمت، از یک فرمول در ریاضیات استفاده میکنیم:
نسبت محیط کمان قطاع به محیط کل دایره = نسبت مساحت قطاع به مساحت کل دایره
محیط قطاع برابر است با محیط قاعده مخروط، یعنی . محیط کل دایره به شعاع l هم میشود و مساحت کل دایره به شعاع l نیز با برابر است. پس اگر مساحت قطاع موردنظر را با Sl نشان دهیم، خواهد شد:
بنابراین محاسبه مساحت سطح جانبی مخروطی با شعاع r و یال l بهصورت انجام شد.
محاسبه مساحت کل مخروط
پس از محاسبه مساحت سطح جانبی، حالا میتوانیم مساحت کل مخروط را با جمع کردن مساحت سطح جانبی و مساحت قاعده مخروط بهدست آوریم. مساحت قاعده مخروط برابر با مساحت دایرهای به شعاع r یعنی است. بنابراین اگر مساحت کل مخروط را با St نشان دهیم، مقدار آن میشود:
محاسبه حجم مخروط
فرمول حجم مخروط از فرمول حجم استوانه بهدست میآید. اما ابتدا باید ببینیم استوانه چیست و حجم آن چگونه محاسبه میشود. استوانه یک شکل هندسی است دارای دو قاعده دایرهای شکل با شعاع یکسان که توسط یک سطح جانبی به هم متصل شدهاند. محور استوانه یا ارتفاع، خطی است که مرکز دو قاعده دایرهای شکل را به هم متصل میکند. در شکل زیر استوانهای با شعاع r و ارتفاع h نشان داده شده است.
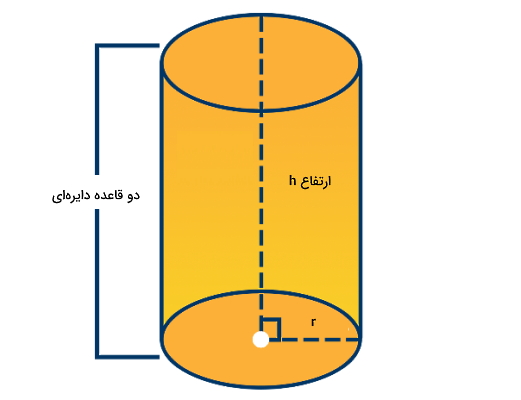
حالا میخواهیم حجم این استوانه را محاسبه کنیم. فرض میکنیم تعداد h عدد دیسک با شعاع r و ارتفاع واحد (اندازه ارتفاع = ۱) داریم. اگر این دیسکها را روی هم بچینیم، در نهایت به استوانهای به شکل زیر میرسیم که دارای شعاع r و ارتفاع h است. در واقع، داخل استوانه با h عدد دیسک به مساحت پر شده است. بنابراین حجم استوانه میشود:
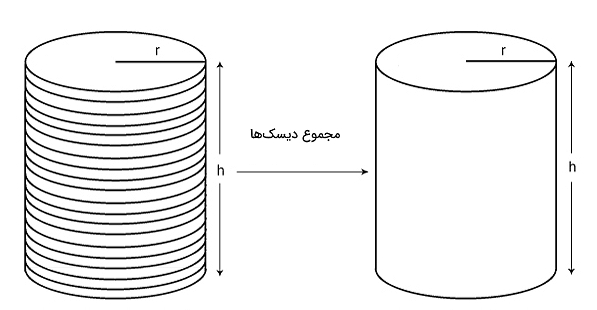
اگر در داخل این استوانه یک مخروط با قاعدهای کاملا برابر با قاعده استوانه و ارتفاعی کاملا برابر با ارتفاع استوانه قرار دهیم، این مخروط دقیقا یک سوم حجم استوانه را پر میکند. بنابراین میتوانیم بگوییم حجم مخروط یک سوم حجم استوانه است. به عبارت دیگر، فرض کنید استوانهای به شعاع r و ارتفاع h کاملا با مایعی پر شده است. اگر بخواهیم مایع داخل این استوانه را داخل مخروطی با شعاع r و ارتفاع h بریزیم، باید سه مخروط مشابه با این ابعاد داشته باشیم تا استوانه کاملا خالی شود.
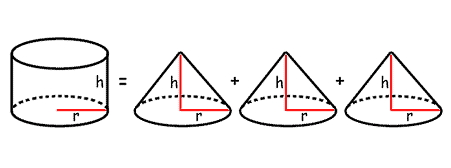
پس اگر حجم مخروط را با V نشان دهیم، فرمول حجم مخروط میشود:
همچنین اگر بخواهیم فرمول حجم مخروط را برحسب اندازه یال ان یعنی l بنویسیم، با توجه به اینکه رابطه بین r و h و l بهصورت است، فرمول زیر را خواهیم داشت:
انواع مخروط
مخروطها در دو گروه کلی «مخروط قائم» (Right Cone) و «مخروط مایل یا اریب» (Oblique Cone) دستهبندی میشوند. عامل تعیینکننده قائم یا مایل بودن مخروط، محل قرارگیری راس مخروط نسبت به قاعده است. همچنین، در اغلب موارد قاعده یک مخروط یک دایره است و به همین علت چنین مخروطهایی را «مخروط دایروی» مینامند. اما در برخی مخروطها، قاعده مخروط به شکل یک «بیضی» (Ellipse) است. در این صورت مخروط را «مخروط بیضوی» مینامیم. در این مطلب، با فرض دایروی بودن مخروطها توضیحات لازم و مثالها بیان شده است.
مخروط قائم چیست؟
بیشتر اوقات زمانی که از کلمه مخروط استفاده میکنیم، منظورمان مخروط قائم است، مگر اینکه تاکید شود مخروط موردنظر مایل است. در مخروط قائم ارتفاع و محور مخروط بر قاعده آن عمود است. به عبارت دیگر، در این نوع مخروط راس مخروط دقیقا بالای مرکز قاعده قرار دارد. نکته مهمی که در مورد مساحت جانبی یک مخروط قائم وجود دارد این است که تمامی خطوطی که راس این مخروط را به قاعده آن وصل میکنند، دارای طول یکسانی هستند.
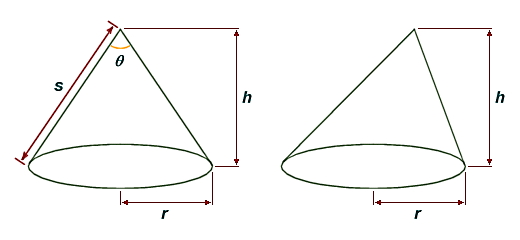
برای محاسبه حجم مخروط قائم از همان فرمولی استفاده میشود که برای حجم مخروط در بخشهای قبلی محاسبه شد. همچنین مساحت سطح جانبی و مساحت کل مخروط قائم نیز همان روابطی هستند که در بخشهای پیش بیان کردیم:
مخروط مایل چیست؟
در مخروط مایل محور مخروط بر قاعده آن عمود نیست. در واقع در این نوع مخروط، راس در هر نقطهای به جز دقیقا در بالای مرکز قاعده قرار میگیرد. در مخروط مایل، خطوطی که راس مخروط را به هر نقطه روی محیط قاعده متصل میکنند، هماندازه نیستند. در شکل بالا میتوانید تفاوت این دو نوع مخروط را بهتر مشاهده کنید.
نکته: فرمولی که برای محاسبه حجم مخروط مایل بهکار میرود، دقیقا همان فرمول حجم مخروط قائم است، اما در مورد مساحت جانبی و مساحت کل مخروط مایل روابط با مخروط قائم یکسان نیست. سوالی که پیش میآید این است که پس مساحت جانبی یک مخروط مایل را چگونه میتوان محاسبه کرد؟ پاسخ این است که فرمول مشخصی برای مساحت جانبی و در نتیجه محاسبه مساحت کل یک مخروط مایل وجود ندارد.
برای نمونه تصویر زیر را در نظر بگیرید. ارتفاع (h) برای مخروط قائم در شکل (A)، از نقطه راس مخروط به مرکز قاعده دایرهای شکل عمود شده است. این تعریفی است که برای ارتفاع در هر مخروط قائمی صدق میکند.
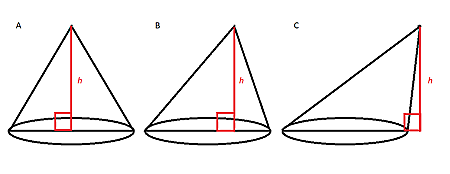
اما در شکلهای (B) و (C) که دو مخروط مایل هستند، ارتفاع تعریف مشابهی ندارد. در شکل (B) خط عمود از راس مخروط به نقطهای روی قاعده دایرهای شکل ارتفاع مخروط شده است، در حالی که در شکل (C) ارتفاع مخروط از راس مخروط به نقطهای خارج از قاعده مخروط عمود شده است. در واقع در این دو مخروط مایل، راس مخروط متفاوت است. همین متفاوت بودن راس در مخروطهای مایل، باعث میشود نتوانیم فرمول مشخصی برای مساحت جانبی آنها پیدا کنیم.
مخروط ناقص چیست؟
«مخروط ناقص» (Frustum Cones) در دستهبندی کلی مخروطها قرار نمیگیرد، اما جز اشکال هندسی پرکاربردی است که شناخت ویژگی آن لازم است. اگر یک مخروط قائم را در نظر بگیرید، با ایجاد یک برش افقی روی محور آن و موازی با سطح مقطع دایرهای شکلاش، یک مخروط کوچکتر و یک بخش ناقص تشکیل میشود. این بخش ناقص، مخروط ناقص نام دارد. در سمت راست تصویر زیر مشاهده میکنید که یک مخروط ناقص چه شکلی خواهد داشت. همانطور که در شکل مشخص است، چنین مخروطی دارای دو قاعده دایرهای شکل و نابرابر است و نقطهای به نام راس مخروط را ندارد.
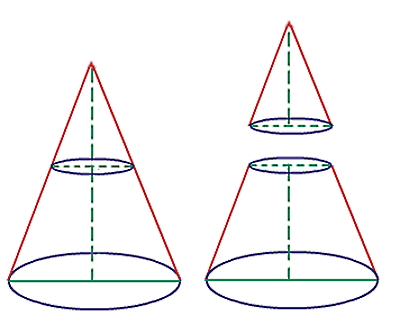
اگر بخواهیم به نمونههای عینی از یک مخروط ناقص در زندگی روزمره اشاره کنیم، آباژور یا سطل گزینههای مناسبی هستند. برای اینکه حجم چنین مخروطی را پیدا کنیم، کافی است حجم مخروط کوچک جدید (مخروط دوم) را از حجم مخروط اولیه بزرگتر (مخروط اول) کم کنیم. اگر شکل زیر را در نظر بگیریم، ابعاد دو مخروط را میتوانیم به صورت زیر بنویسیم:
- شعاع مخروط اول: r
- اندازه یال مخروط اول: l
- ارتفاع مخروط اول: h+H
- شعاع مخروط دوم: 'r
- اندازه یال مخروط دوم: 'l
- ارتفاع مخروط دوم: h
با توجه به این اطلاعات، حجم مخروط اول و دوم خواهد شد:
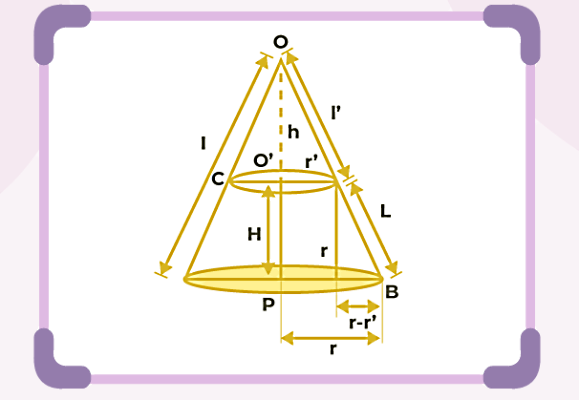
با کم کردن حجم مخروط دوم از اول، حجم مخروط ناقص یعنی V بهصورت زیر حاصل میشود:
حالا برای اینکه این رابطه را سادهتر کرده باشیم، از قواعد تشابه مثلثها استفاده میکنیم. دو مثلث OPB و OO'C را در نظر میگیریم. طبق قواعد تشابه، برای این دو مثلث رابطه زیر برقرار است:
حالا بهجای h+H، در فرمولی که برای حجم مخروط ناقص بهدست آوردیم، این مقدار را قرار میدهیم:
مجددا به نسبت تشابه بازمیگردیم:
حالا بهجای h در فرمول حجم، این رابطه را قرار میدهیم:
در این بخش از یک فرمول معروف در اتحاها به نام فرمول اتحاد چاق و لاغر استفاده میکنیم. طبق این فرمول داریم:
پس میتوانیم بهجای بنویسیم :
پس فرمول مخروط ناقص با شعاع قاعده کوچکتر یا قاعده بالایی 'r و شعاع قاعده بزرگتر یا قاعده پایینی r میشود:
که در آن H ارتفاع مخروط ناقص است. ارتفاع مخروط ناقص، فاصله بین دو مرکز قاعده دایرهای شکل است. پس برای محاسبه حجم مخروط ناقص، کافی است اندازه شعاع دو قاعده و ارتفاع مخروط را بدانیم.
مثال فرمول حجم مخروط
پس از اینکه یاد گرفتیم فرمول حجم مخروط چیست و محاسبه حجم مخروط به چه صورت انجام میشود، در این بخش قصد داریم با حل مثالهای متنوع نکات این مبحث را تکمیل کنیم.
مثال ۱
حجم مخروطی با شعاع ۲ cm و ارتفاع ۵ cm چقدر است؟
پاسخ
از فرمول حجم مخروط استفاده میکنیم و r=۲ و h=۵ را جایگزین میکنیم:
میدانیم مقدار عدد پی برابر است با ۳٫۱۴. بنابراین داریم:
مثال ۲
اگر ارتفاع یک مخروط ۷ cm و قطر سطح مقطع آن ۶ cm باشد، حجم مخروط را پیدا کنید:
پاسخ
میدانیم سطح مقطع یک مخروط، دایره است. بنابراین اگر قطر آن به ما داده شده است، با توجه به اینکه در فرمول حجم مخروط شعاع داریم، لازم است قطر دایره را به شعاع تبدیل کنیم. شعاع یک دایره، همیشه نصف قطر آن است. پس با در نظر گرفتن قطر دایره بهصورت d، داریم:
همچنین با حل این مثال میتوانیم برای حجم مخروط بر حسب قطر قاعده دایرهای شکل (d) فرمول مستقیمی بیان کنیم که بهصورت زیر است:
مثال ۳
اگر حجم مخروطی برابر با ۱۷۴٫۴ m۳ و ارتفاع آن ۸٫۶ m باشد، مساحت قاعده و شعاع مخروط چقدر است؟
پاسخ
در این مسئله بهتر است از فرمول حجم مخروط بهصورت زیر استفاده کنیم:
که در آن ، مساحت قاعده دایرهای شکل در مخروط است.
پس مساحت قاعده محاسبه شد. حالا برای پیدا کردن شعاع قاعده، از فرمول مساحت دایره استفاده میکنیم:

مثال ۴
مساحت سطح جانبی مخروطی با شعاع قاعده ۱ cm و ارتفاع ۳ cm، چقدر است؟
پاسخ
میدانیم فرمول مساحت جانبی مخروط برابر است با . در این رابطه l یعنی اندازه یال مخروط برابر است با . بنابراین اول باید l را محاسبه کنیم:
حالا عدد بهدست آمده را در فرمول مساحت جانبی مخروط قرار میدهیم:
مثال ۵
اگر نسبت ارتفاع دو مخروط قائم ۱ به ۵ و نسبت محیط قاعده آنها نیز ۵ به ۳ باشد، نسبت حجم این دو مخروط را بیابید:
پاسخ
مخروطها را با شماره ۱ و ۲ نامگذاری میکنیم تا بتوانیم راحتتر به پاسخ این سوال برسیم. در این سوال محیط قاعده مخروط داده شده است. پس باید فرمول حجم مخروط را بر حسب محیط قاعده بازنویسی کنیم تا بهتر بتوانیم از نسبتهای داده شده استفاده کنیم. برای حجم هر کدام از دو مخروط داریم:
محیط قاعده مخروط را که یک دایره است، با P نشان میدهیم. حالا نسبتهایی که در صورت سوال داده شده است را بهصورت زیر مرتب میکنیم:
می دانیم محیط دایره برابر است با ، پس اگر فرمول حجم مخروط را بر حسب P بخواهیم بنویسیم، خواهیم داشت:
حالا میتوانیم نسبت حجم دو مخروط را با هم مقایسه کنیم:
در این نسبت، اعداد ثابت که مشترک هستند، حذف میشوند. در نهایت پس از سادهسازی داریم:
حالا میتوانیم نسبتهای داده شده در صورت سوال را بهراحتی جایگذاری کنیم:
بنابراین نسبت حجم مخروط اول به دوم برابر با ۵ به ۹ است.
مثال ۶
اگر محیط قاعده یک مخروط قائم ۸۸ cm و ارتفاع آن ۴۸ cm باشد، مساحت کل مخروط را محاسبه کنید:
پاسخ
محیط قاعده مخروط برابر است با محیط دایره. پس از فرمول محیط دایره استفاده میکنیم تا با قرار دادن ۸۸ بهجای محیط، شعاع قاعده مخروط را پیدا کنیم:
حالا اگر فرمول مساحت کل مخروط را در نظر بگیریم، هنوز l را نداریم. پس اول l را از قضیه فیثاغورس محاسبه میکنیم:
حالا مقادیر l و r را در فرمول St قرار میدهیم:
مثال ۷
مساحت سطح جانبی یک مخروط ۱ و ۱/۳ برابر بزرگتر از مساحت قاعده آن است. اگر ارتفاع مخروط ۷ cm باشد، حجم مخروط چقدر است؟
پاسخ
اگر مساحت جانبی را با St و مساحت قاعده مخروط را با Sb نشان دهیم، جمله اول در صورت سوال به معنای زیر است:
حالا دو فرمول مساحت را در فرمول اول که رابطه دو مساحت است، قرار میدهیم:
پس از سادهسازی خواهیم داشت:
حالا با توجه به اینکه نسبت l به r و ارتفاع h را داریم، میتوانیم مقدار r را حساب کنیم. چون برای محاسبه حجم مخروط، باید شعاع را داشته باشیم. اگر از رابطه بالا l را خارج کنیم و قضیه فیثاغورس را استفاده کنیم، داریم:
حالا که r پیدا شد، میتوانیم به محاسبه حجم مخروط بپردازیم:

مثال ۸
اگر مقادیر یال و شعاع یک مخروط قائم نسبت ۲۹ به ۲۰ داشته باشند و حجم مخروط برابر با ۴۸۳۸٫۴ π cm۳ باشد، شعاع مخروط چقدر است؟
پاسخ
ابتدا نسبت یال به شعاع را بهصورت مینویسیم. بنابراین داریم:
اگر قضیه فیثاغورس را برای یال مخروط بنویسیم، خواهیم داشت:
بنابراین تا اینجا ارتفاع را بر حسب شعاع مخروط محاسبه کردیم. حالا اگر از فرمول حجم مخروط استفاده کنیم، بهجای h در این فرمول رابطه بالا را قرار دهیم و مقدار حجم داده شده در صورت سوال را بهجای V جایگزین کنیم، خواهیم داشت:
پس از سادهسازی عبارت بالا، r۳ را خواهیم داشت:
و با گرفتن ریشه سوم عدد بهدست آمده برای r۳، شعاع مخروط محاسبه خواهد شد:
مثال ۹
حجم مخروط ناقصی با دو قاعده به شعاعهای ۱ و ۲ و ارتفاع ۵ چند است؟
پاسخ
میدانیم فرمول حجم مخروط ناقص برابر است با:
با جایگذاری عددها در این فرمول، حجم میشود:
مثال ۱۰
در یک مخروط قائم، شعاع قاعده مخروط ۱۴ cm است و ارتفاع آن ۴۸ cm. فرض کنید برشی در این مخروط درست از نقطه میانی ارتفاع مخروط و موازی با قاعده آن، انجام شود. در این صورت حجم نیمه بالایی که یک مخروط کوچکتر است، چقدر است؟
پاسخ
در حل این سوال لازم است از این نکته استفاده کنیم که وقتی مخروطی از وسط برش داده میشود، نسبت حجم مخروط کوچکتر به حجم مخروط بزرگتر برابر است با مکعب نسبت ارتفاع این دو مخروط. در سوال گفته شده است که برش از نقطه وسط ارتفاع مخروط اولیه انجام شده است. بنابراین مطابق شکل زیر، دو مخروط در نهایت خواهیم داشت، یک مخروط کوچکتر با نام APD و یک مخروط بزرگتر به نام ABC.
فرض میکنیم ارتفاع مخروط کوچکتر h و ارتفاع مخروط بزرگتر H است. در این صورت حجم مخروط بزرگتر میشود:
که با داشتن مقدار شعاع و ارتفاع این مخروط، حجم آن بهراحتی محاسبه میشود:
حالا با توجه به اینکه مخروط از نیمه ارتفاع خود برش داده شده است، پس ارتفاع مخروط کوچک بالایی برابر است با . طبق توضیحی که در ابتدای حل این سوال دادیم، نسبت حجم مخروط کوچکتر به حجم مخروط بزرگتر برابر است با مکعب نسبت ارتفاع این دو مخروط یعنی . به عبارتی اگر حجم مخروط کوچکتر را با v نشان دهیم، میتوانیم بنویسیم:
تکمیل یادگیری حجم مخروط با فرادرس
در این بخش لیستی از فیلمهای آموزشی فرادرس برای دانشجویان علاقهمند به مبحث اشکال هندسی تهیه شده است. با مشاهده این فیلمهای فرادرس میتوانید اطلاعات تکمیلی در این زمینه کسب کنید:
- فیلم آموزش ریاضی عمومی ۲ مرور و حل تمرین فرادرس
- فیلم آموزش ریاضی عمومی ۲ حل مثال فرادرس
- فیلم آموزش رایگان محاسبه حجم، مکعب، هرم، مخروط و کره فرادرس
آزمون حجم مخروط
پس از آموختن تمام نکات مربوط به فرمول حجم مخروط، در انتهای این مطلب از مجله فرادرس میتوانید با حل سوالات آزمون، میزان یادگیری خود را محک بزنید. پس از انتخاب تمام گزینههای موردنظر، با کلیک بر روی بخش «دریافت نتیجه آزمون»، نمره نهایی خود را مشاهده خواهید کرد.
ارتفاع و شعاع یک مخروط به ترتیب برابر هستند با ۱۵ cm و ۷ cm. حجم این مخروط کدام گزینه است؟
گزینه آخر صحیح است. با استفاده از فرمول حجم مخروط، میتوانیم به این سوال پاسخ دهیم:
برای دوخت یک چادر مخروطی شکل مسافرتی بدون در نظر گرفتن زیره و با ارتفاع ۴۸ m و شعاع سطح مقطع ۱۴ m، چند متر پارچه لازم است اگر عرض پارچه ۸ m باشد؟
۲۷۵
۲۲۰
۲۶۴
۲۵۷
گزینه اول درست است. مقدار پارچهای که برای دوخت این چادر لازم است، همان مساحت سطح جانبی چادر مخروطی شکل است. چون گفته شده زیره در نظر گرفته نشود، یعنی مساحت قاعده از مساحت سطح کل مخروط کم شده است. بنابراین مساحت سطح جانبی باقی میماند.
پس در واقع باید از فرمول مساحت سطح جانبی مخروط یعنی استفاده کنیم. اما در این فرمول از l استفاده شده است که هنوز مقدار آن را نمیدانیم. پس ابتدا l را از قضیه فیثاغورس بهدست میآوریم:
حالا با داشتن l و r میتوانیم مساحت سطح جانبی این چادر مخروطی شکل را محاسبه کنیم:
از طرفی باید طبق صورت سوال، عرض پارچه استفاده شده را نیز در نظر بگیریم. پارچه استفاده شده به شکل مستطیل است. میدانیم مساحت مستطیل برابر است با حاصلضرب طول در عرض آن. پس اگر مساحت پارچه موردنیاز برابر با ۲۲۰۰ m۲ باشد، در حالی که عرض پارچه ۸ m است، آنگاه طول موردنیاز برابر خواهد شد با:
یک کلاه مخروطی شکل قطری برابر با ۲۴ cm و ارتفاع ۱۶ cm دارد. هزینه نقاشی روی سطح این کلاه چقدر خواهد شد، اگر نرخ پرداختی برای هر cm۲ از سطح این کلاه معادل ۱۰۰۰ تومان باشد؟
۷۵۳٫۶ تومان
۷۵۳۶۰۰۰ تومان
۷۵۳۶۰۰ تومان
۷۵۳۶ تومان
گزینه سوم درست است. در این سوال هم با توجه به اینکه کلاه مخروطی شکل، در واقع همان مخروطی است که قاعده ندارد، پس در سوال مساحت سطح جانبی مخروط خواسته شده است. همچنین میدانیم قطر دایره برابر است با دو برابر شعاع آن. پس شعاع مخروط خواهد شد:
از طرفی باید یال مخروط را هم حساب کنیم:
مساحت سطح جانبی مخروط نیز بهصورت زیر محاسبه میشود:
هزینه نقاشی برای هر سانتیمتر مربع در سوال داده شده است. هزینه نقاشی کل این سطح، از ضرب ۷۰ در عدد بالا بهدست میآید:
محیط قاعده یک مخروط با ارتفاع ۱۶ cm برابر است با ۳۳ cm. حجم مخروط کدام گزینه است؟
۱۰۲۸
۶۱۶
۴۶۲
۸۲۸
گزینه سوم درست است. برای محاسبه حجم مخروط باید شعاع و ارتفاع مخروط را داشته باشیم. در این سوال ارتفاع مخروط داده شده است، اما شعاع را از محیط قاعده باید بهدست آوریم. اگر محیط قاعده را که یک دایره است، با P نشان دهیم، خواهیم داشت:
حالا میتوانیم فرمول حجم مخروط را بنویسیم و آن را حساب کنیم:
مینا در حال بررسی یک کیف مخروطی شکل است تا بتواند خطکشی با طول ۸٫۳ اینچ را در آن قرار دهد. اگر او بداند که حجم کیف ۲۴π in۳ و شعاع آن ۳ in است، آیا مینا میتواند بدون امتحان کردن کیف و فقط از طریق محاسبه متوجه شود که خطکش در این کیف قرار میگیرد یا خیر؟ کدام گزینه صحیح است؟
بله، مینا با انجام محاسبات متوجه میشود که خطکش در کیف قرار نمیگیرد، چون طول خطکش از ارتفاع یا قطر کیف مخروطی بیشتر است.
خیر، مینا با انجام محاسبات نمیتواند متوجه شود که آیا خطکشاش درون این کیف قرار میگیرد یا نه.
بله، مینا با انجام محاسبات متوجه میشود که خطکش در کیف قرار نمیگیرد، چون طول خطکش از یال کیف مخروطی بیشتر است.
بله، مینا با انجام محاسبات متوجه میشود که خطکش در کیف قرار میگیرد، چون طول خطکش از یال کیف مخروطی کمتر است.
گزینه آخر درست است. برای اینکه ببینیم خطکش مینا درون این کیف قرار میگیرد یا نه، اول باید ببینیم طول خطکش از ابعاد مختلف این کیف بیشتر است یا کمتر. برای مثال اگر قطر قاعده دایرهای شکل این کیف را حساب کنیم، برابر میشود با . پس تا اینجا طول خطکش (۸٫۳) از قطر کیف (۶) بیشتر است و نمیتواند در این بعد کیف جای بگیرد.
قدم بعدی این است که ارتفاع کیف مخروطی را حساب کنیم و ببینیم ارتفاع کیف از طول خطکش بیشتر میشود یا نه. برای اینکه ارتفاع را پیدا کنیم، میتوانیم از مقدار حجم کیف استفاده کنیم و با بهکار بردن فرمول حجم مخروط، ارتفاع را بهدست آوریم:
ارتفاع کیف هم محاسبه شد و دیدیم که ارتفاع (۸) از طول خطکش (۸٫۳) کمتر است. پس خطکش را به این شکل هم نمیتوانیم داخل کیف قرار دهیم. اما یک بعد دیگر از کیف مخروطی شکل، یال آن است. میدانیم اندازه یال مخروط طبق فرمول زیر از ارتفاع و شعاع آن حساب میشود:
اندازه یال (۸٫۵) از طول خطکش (۸٫۳) بیشتر است. پس اگر خطکش را بهصورت مایل در قسمت یال این کیف مخروطی شکل قرار دهیم، کاملا داخل کیف قرار میگیرد. بنابراین گزینه آخر درست است.
چنانچه بخواهیم داخل یک استوانه با حجم ۲۷π cm۳ و ارتفاع ۳ cm را با تعدادی مخروط پر کنیم، چند مخروط لازم داریم و شعاع این مخروطها چقدر باید باشد؟
سه مخروط با شعاع ۹
سه مخروط با شعاع ۳
دو مخروط با شعاع ۳
نمیتوانیم تعداد مخروطها را مشخص کنیم.
گزینه صحیح، گزینه دوم است. در این سوال بدون اینکه بخواهیم محاسبهای انجام دهیم، طبق مطالب گفته شده در بخش «محاسبه حجم مخروط»، میدانیم حجم یک استوانه سه برابر حجم مخروطی با ابعاد یکسان است. پس گزینه اول و دوم تا اینجا درست هستند.
اما برای اینکه سه مخروط داخل استوانه قرار بگیرند، باید شعاع و ارتفاع آنها کاملا با شعاع و ارتفاع استوانه برابر باشد. اگر شعاع استوانه را حساب کنیم، شعاع مخروط هم همین است.
پس فرمول حجم استوانه را بهکار میبریم و بهجای حجم و ارتفاع از صورت سوال عددگذاری میکنیم:
اگر شعاع و ارتفاع مخروطی دو برابر شود، حجم آن چه تغییری خواهد کرد؟
حجم چهار برابر میشود.
حجم هم دو برابر میشود.
حجم هشت برابر میشود.
حجم تغییری نمیکند.
گزینه سوم درست است. اگر شعاع اولیه مخروط r۱ و شعاع جدید برابر با r۲ شود و به همین ترتیب ارتفاع اولیه h۱ و ارتفاع در حالت دوم h۲ شود، طبق فرمول حجم مخروط خواهیم داشت:
با محاسبه نسبت حجم در حالت دوم به حجم در حالت اول، میتوانیم تغییرات حجم را پیدا کنیم:
پس از سادهسازی داریم:
اگر در مخروطی به شعاع ۵ cm و ارتفاع ۸ cm، یک برش افقی موازی قاعده و در فاصله ۲ cm از راس ایجاد شود، حجم مخروط ناقص حاصل شده با شعاع قاعده کوچکتر ۱ cm کدام گزینه است؟ (π=۳)
پاسخ صحیح، گزینه آخر است. فرمول حجم مخروط ناقص برابر است با:
در این سوال r برابر است با ۵، 'r که همان شعاع قاعده بالایی یا قاعده کوچکتر است برابر است با ۱ و ارتفاع مخروط ناقص یا H برابر میشود با ارتفاع مخروط اولیه منهای ارتفاع مخروط کوچک ثانویه یعنی ۲-۸ که برابر است با ۶. با قرار دادن این اعداد در فرمول داریم:
دقت شود در صورت سوال ذکر شده است که عدد پی برابر با ۳ در نظر گرفته شود.
کدام گزینه درست نیست؟
حجم یک مخروط، ۳ برابر حجم استوانهای با ابعاد مشابه است.
مخروط نوعی هرم است، با این تفاوت که قاعده آن به جای چندضلعی یک دایره است.
یک مخروط ناقص دارای دو قاعده دایرهای شکل است.
یک مخروط مایل فرمول حجم مشخصی دارد ولی فرمول مساحت جانبی آن مشخص نیست.
گزینه اول اشتباه است و جابجا بیان شده است. حجم یک مخروط یک سوم حجم استوانهای با ابعاد مشابه است. سایر گزینهها درست هستند.
مساحت کل یک مخروط کدام گزینه است؟
گزینه اول درست است. گزینه دوم مساحت جانبی مخروط، گزینه سوم مساحت قاعده مخروط و گزینه آخر فرمول حجم مخروط است.