اشکال هندسی | تعاریف، فرمول های محاسبه محیط و مساحت – به زبان ساده


در این مطلب از مجله فرادرس که راهنمایی برای اشکال هندسی است، با انواع شکلهای هندسی آشنا میشویم و علاوه بر بیان تعریف آنها، فرمولهای محاسبه مساحت، محیط و حجمشان را ارائه میکنیم.
دایره
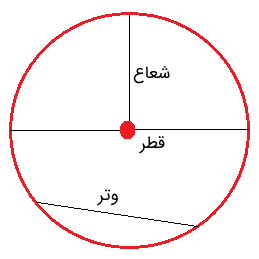
«دایره» (Circle) به مجموعه نقاطی از یک صفحه گفته میشود که فاصله یکسانی از یک نقطه مرکزی دارند. دایره تنها از نقاط مرزی تشکیل میشود. فاصله بین نقطه میانی و مرز دایره را «شعاع» مینامند. پارهخطی که نقاط انتهایی آن روی دایره باشد و از نقطه میانی عبور کند «قطر» نامیده میشود.
قطر دو برابر شعاع است. همچنین، پارهخطی را که نقاط انتهایی آن روی مرز دایره قرار دارند، اما از مرکز عبور نمیکند، «وتر» مینامیم.
مساحت دایره
دایره زیر را در نظر بگیرید.
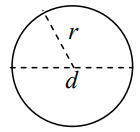
مساحت یک دایره با شعاع برابر است با:
همچنین، مساحت یک دایره با قطر به صورت به دست میآید:
محیط دایره
محیط دایرهای به شعاع به صورت زیر به دست میآید:
اگر قطر دایره را داشته باشیم، محیط آن به صورت زیر محاسبه میشود:
مثلث
مثلث یکی از اشکال هندسی مهم است، زیرا سایر چندضلعیها (با تعداد ضلعهای بیشتر از ۳) به مثلث قابل تجزیه هستند.
جالب است بدانید که مثلث تنها چندضلعی است که اگر اندازه اضلاع آن را داشته باشیم، یک شکل منحصر به فرد خواهیم داشت. سه نوع مثلث در شکل زیر نشان داده شدهاند.
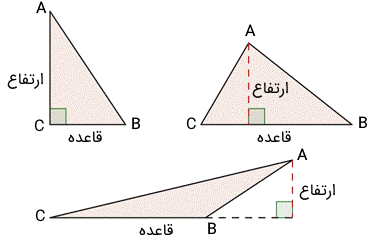
ضلع مثلث پارهخطی است که دو رأس مجاور مثلث را به هم متصل میکند. رأس، محل برخورد دو ضلع مثلث است. ارتفاع: یک پارهخطی است که از یک رأس آغاز میشود و بر ضلع مقابل (یا امتداد آن) عمود است. محل برخورد ارتفاع با قاعده یا امتداد آن، پای عمود نام دارد. همچنین، قاعده مثلث ضلعی است که ارتفاع بر آن عمود میشود.
مساحت مثلث
مثلث زیر را در نظر بگیرید.
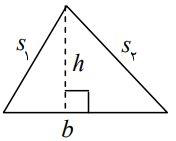
مساحت مثلث بالا به ارتفاع و قاعده به صورت زیر محاسبه میشود:
محیط مثلث
محیط مثلث با ساقهای و و قاعده برابر است با:
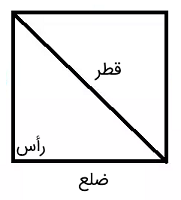
مربع
مربع یکی از اشکال هندسی با چهار ضلع مساوی است که هر چهار زاویه آن برابر با 90 درجه است. مستطیل تقریباً ویژگیهای مشابهی با یک مربع دارد، اما تفاوت این دو شکل در این است که در یک مستطیل فقط اضلاع مقابل با هم برابرند و اندازه اضلاع مجاور آن با هم برابر نیست. بنابراین، مستطیل تنها در صورتی مربع خوانده میشود که طول هر چهار ضلع آن برابر باشد. در واقع، میتوان چنین گفت که مربع نوع خاصی از یک مستطیل است.
قطر مربع یک پارهخط است که دو رأس مقابل مربع را به هم موصل میکند. رأس محل برخورد دو ضلع مجاور مربع است. از آنجا که هر مربع چهار رأس دارد، بنابراین در یک مربع دو قطر وجود خواهد داشت.
مساحت مربع
مربع زیر را در نظر بگیرید.

مساحت این مربع به ضلع به صورت زیر به دست میآید:
محیط مربع
محیط مربع نیز به صورت زیر محاسبه خواهد شد:
مستطیل
مستطیل یک چهارضلعی که دو جفت ضلع دارد که طول اضلاع روبهروی آن با یکدیگر برابرند.
در مستطیل هر چهار زاویه داخلی قائمه هستند.
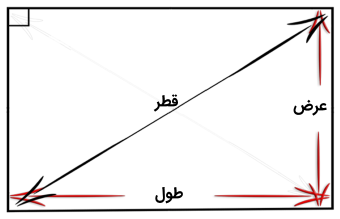
ضلع کوچک مستطیل عرض نامیده میشود و ضلع بزرگ آن را طول مینامیم. قطر مستطیل نیز، یک پارهخط است که دو رأس مقابل را به هم وصل میکند.
مساحت مستطیل
مستطیل زیر را در نظر بگیرید.
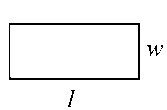
مساحت این مستطیل برابر است با:
محیط مستطیل
محیط مستطیلی به طول و عرض برابر است با:
لوزی
لوزی یکی از اشکال هندسی چهارضلعی است که اندازه هر چهار ضلع آن با هم برابر است.
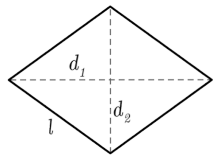
همانطور که در شکل بالا میبینیم، قطرهای لوزی عمود منصف یکدیگر هستند.
مساحت لوزی
مساحت یک لوزی با قطرهای و برابر است با:
محیط لوزی
محیط یک لوزی به ضلع برابر است با:
متوازی الاضلاع
متوازی الاضلاع یکی از اشکال هندسی چهارضلعی است که اضلاع روبهروی آن موازی یکدیگرند. اندازه اضلاع و زوایای روبهرو در متوازیالاضلاع با هم برابر است. در متوازی الاضلاع شکل زیر، قاعده است که معمولاً (نه همیشه) در قسمت پایین و کف شکل است.
ارتفاع متوازی الاضلاع است که خطی را نشان میدهد که از قاعده بالا بر قاعده پایین عمود میشود. قطر متوازی الاضلاع نیز پارهخطی است که دو رأس مقابل را به هم وصل میکند.
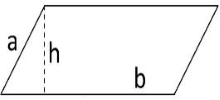
مساحت متوازی الاضلاع
مساحت متوازیالاضلاعی با ارتفاع و قاعده با فرمول زیر به دست میآید:
محیط متوازی الاضلاع
اگر دو ضلع متوالی یک متوازیالاضلاع برابر با و باشند، محیط آن برابر خواهد بود با:
ذوزنقه
ذوزنقه یکی از اشکال هندسی چهارضلعی است که دو ضلع آن با هم موازی هستند.
دو ضلع موازی ذوزنقه را قاعده مینامند و دو ضلع دیگر ساقهای آن هستند.
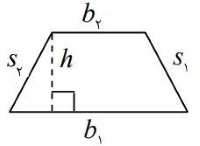
کوتاهترین فاصله بین دو قاعده را ارتفاع مینامند.
مساحت ذوزنقه
اگر ارتفاع ذوزنقه را و قاعدههای آن را و و ساقهایش را و فرض کنیم، مساحت آن برابر خواهد بود با:
محیط ذوزنقه
محیط ذوزنقهای با قاعدههای و و ساقهای و برابر است با:
بیضی
بیضی یکی از اشکال هندسی و مقاطع مخروطی است که از تقاطع مخروط با صفحهای که نسبت به قاعده مخروط زاویه دارد، ساخته میشود.
در واقع، بیضی مجموعه تمام نقاطی از صفحه است که مجموع فاصله آنها از دو نقطه ثابت (که کانون نامیده میشوند) یک مقدار ثابت است. در شکل زیر، F و G کانونهای بیضی هستند و P نقطهای از مکان هندسی بیضی است.
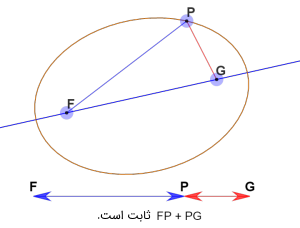
در شکل زیر، قطر بزرگ و قطر کوچک بیضی هستند.
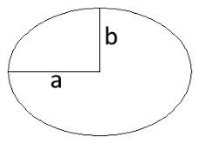
مساحت بیضی
مساحت یک بیضی با قطر کوچک و قطر بزرگ با فرمول زیر محاسبه میشود:
محیط بیضی
روشهای مختلفی برای تقریب محیط بیضی وجود دارد. محیط تقریبی بیضی برابر است با:
n ضلعی
n ضلعی، همانگونه که از نامش پیداست، یکی از اشکال هندسی است که n ضلع دارد.
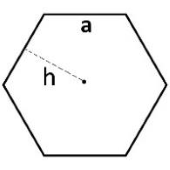
مساحت n ضلعی
مساحت یک n ضلعی با ارتفاع و طول ضلع به صورت زیر محاسبه میشود:
محیط n ضلعی
محیط یک n ضلعی به طول ضلع برابر است با:
کره
کره یکی از اشکال هندسی سهبعدی گرد و متقارن حول یک نقطه است.
همه نقاط سطح کره فاصله یکسانی از مرکز کره دارند. این فاصله شعاع نامیده میشود و در شکل زیر با مشخص شده است. قطر کره نیز پارهخطی است که از مرکز کره عبور کرده و دو نقطه از سطح کره را به یکدیگر وصل میکند.
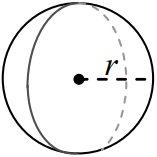
مساحت سطح کره
مساحت سطح کرهای به شعاع برابر است با:
مساحت سطح کرهای به قطر به صورت زیر به دست میآید:
حجم کره
حجم کرهای با شعاع به صورت زیر محاسبه میشود:
مکعب مستطیل
مکعب مستطیل یکی از اشکال هندسی سهبعدی است که ۸ رأس، ۱۲ ضلع و ۶ وجه دارد. تمام وجههای روبهرو در مکعب مستطیل برابر هستند. همچنین، مکعب مستطیل دارای مقاطع مستطیلی است.
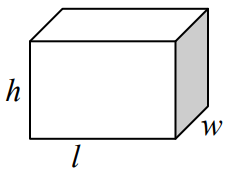
حجم مکعب مستطیل
حجم مکعب مستطیل شکل بالا به ارتفاع ، طول و عرض برابر است با:
مساحت مکعب مستطیل
مساحت سطح مکعب مستطیلی به ارتفاع ، طول و عرض برابر است با:
استوانه
استوانه یکی از اشکال هندسی سهبعدی است که دو دایره موازی و هماندازه در بالا و پایین دارد. این دایرهها را قاعده مینامیم. فاصله بین دو قاعده را نیز ارتفاع میگوییم. اگر قاعدههای بالا و پایین استوانه در یک راستا باشند، استوانه را قائم و اگر بر هم منطبق نباشند، استوانه را مایل مینامیم. شکل زیر استوانه مایل و قائم را نشان میدهد.

استوانه زیر را داریم.
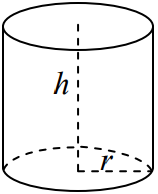
حجم استوانه
حجم استوانهای با ارتفاع و شعاع قاعده برابر است با:
مساحت استوانه
اگر یک استوانه دارای ارتفاع و شعاع قاعده باشد، مساحت سطح آن به شکل زیر محاسبه میشود:
مخروط
مخروط یکی از اشکال هندسی سهبعدی است که از سطح مقطع به آرامی یا به سرعت (بسته به سطح قاعده و ارتفاع) تا رأس باریک میشود. شکل زیر یک مخروط را نشان میدهد.
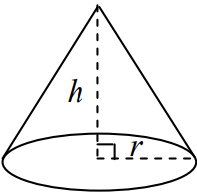
حجم مخروط
حجم مخروطی به شعاع قاعده و ارتفاع ، برابر است با:
مساحت سطح مخروط
مساحت سطح یک مخروط که شعاع قاعده آن و ارتفاعش است، به صورت زیر محاسبه میشود:
مخروط ناقص
شکل زیر یکی از اشکال هندسی به نام مخروط ناقص را نشان میدهد که تفاوت آن با مخرط کامل این است که قسمت بالای آن بریده و جدا شده است.

حجم مخروط ناقص
حجم یک مخروط ناقص با ارتفاع ، شعاع قاعده بالای و شعاع قاعده پایین برابر است با:
مساحت سطح مخروط ناقص
حجم یک مخروط ناقص با طول شیب ، شعاع قاعده بالای و شعاع قاعده پایین برابر است با:
منشور
منشور یکی از اشکال هندسی فضایی است که دو وجه از وجههای آن مشابه هستند و به آنها قاعده میگوییم. قاعدههای منشور میتوانند اشکال هندسی مسطح مانند مثلث، مربع، مستطیل یا هر چندضلعی دیگری باشند.
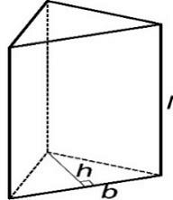
وجوه دیگر منشور مستطیل یا متوازیالاضلاع هستند. دقت کنید که قاعدههای منشور انحنا ندارند و باید چندضلعی باشند.
حجم منشور
حجم منشوری به طول و قاعده و ارتفاع قاعده برابر است با:
مساحت منشور
مساحت سطح منشوری به طول و قاعده و ارتفاع قاعده برابر است با:
bh، مساحت جانبی منشور را نمایش میدهد.









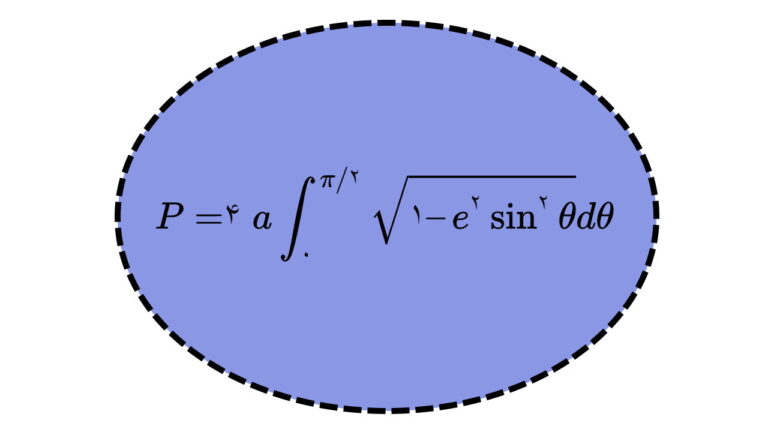

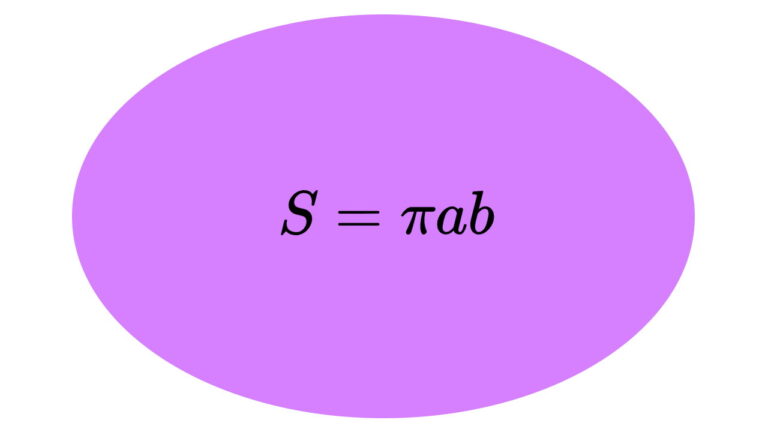

تشکر بابت نشر اطلاعات
سلام و عرض ادب خسته نباشید؛ مطالب بسیار عالی بود آقای مهندس حمیدی؛ ممنون و متشکرم از لطفتان.
کم بود
سلام ممنون آقای حمیدی
عالی بود….