مقاطع مخروطی در مختصات قطبی | به زبان ساده
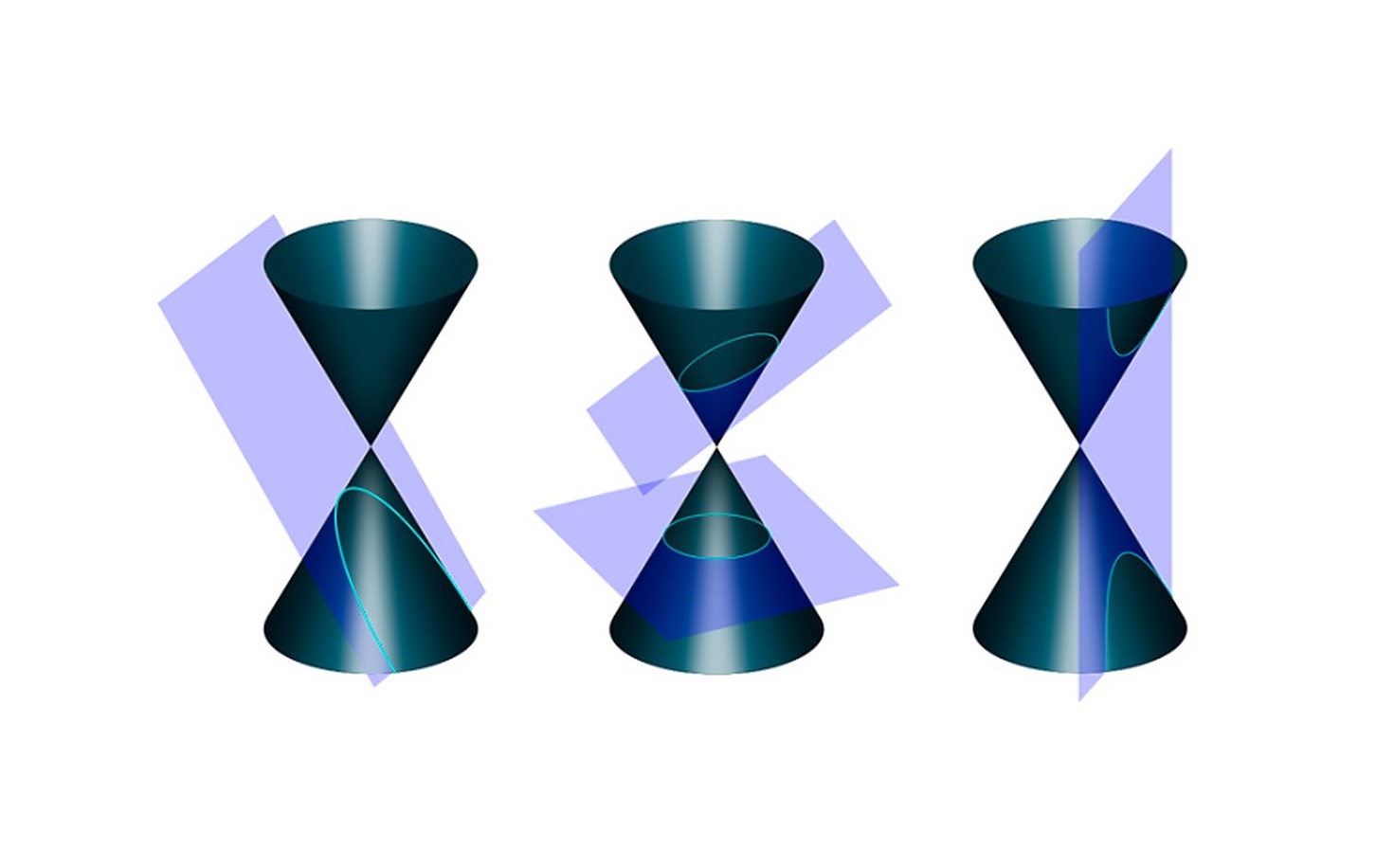
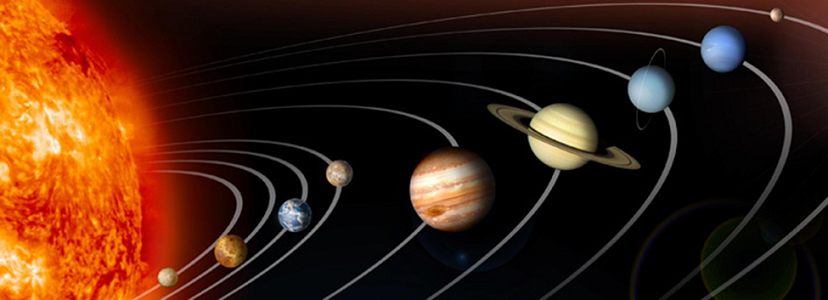
اغلب ما با حرکتِ مداری، مانند حرکت یک سیاره حول خورشید یا الکترون حول هسته اتم آشنا هستیم. درون سامانه سیارهای، مدار سیارات، سیارکها و دنبالهدارها در اطراف اجرام آسمانی بزرگتر اغلب بیضوی هستند. با این حال، دنبالهدارها میتوانند به جای آن در یک مدار سهموی یا هذلولی بگیرند و در واقعیت، ویژگیهای مدار سیارات ممکن است با گذشت زمان تغییر کند. هر مدار با موقعیت جرم آسمانی و فاصله و جهت سیاره یا جسم دیگر از آن جرم گره خورده است. در نتیجه، تمایل داریم از مختصات قطبی برای نشان دادن این مدارها استفاده کنیم. در این آموزش، با مقاطع مخروطی در مختصات قطبی آشنا میشویم.
در مدار بیضوی، «حضیض» (Periapsis) نقطهای است که در آن دو جسم نزدیکتر هستند و «اوج» (Apoapsis) نقطهای است که در آن از هم دورترین فاصله را دارند. به طور کلی، با نزدیک شدن به حضیض، سرعت جرم در مدار افزایش مییابد و با نزدیک شدن به اوج، سرعت آن کم میشود. برخی از اشیاء به سرعت فرار میرسند و این منجر به یک مدار بینهایت میشود. این اجرام حول یک مدار سهموی یا هذلولی میچرخند. جرم در حال چرخش از کشش گرانشی جرم آسمانی جدا میشود و به فضا پرتاب میشود. هر یک از این مدارها را میتوان با یک بخش مخروطی در سیستم مختصات قطبی مدل کرد.
انواع مقاطع مخروطی در مختصات قطبی
هر مخروط را میتوان با سه ویژگی مشخص کرد: یک «کانون» (Focus) منفرد، یک خط ثابت به نام «هادی» (Directrix)، و نسبت مسافت هریک از آنها نسبت به یک نقطه از نمودار.
سهمی $$x=2+y^2$$ را در نظر بگیرید که در شکل ۲ نشان داده شده است.
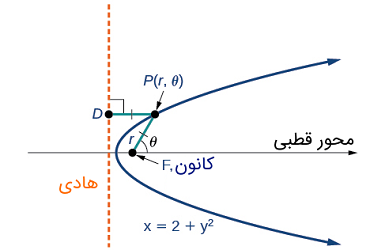
از قبل آموختهایم که چگونه یک سهمی توسط کانون (یک نقطه ثابت) و هادی (یک خط ثابت) تعریف میشود. در این بخش یاد خواهیم گرفت که چگونه هر مخروط را در سیستم مختصات قطبی با یک نقطه ثابت، کانون $$P(r,\theta)$$ در قطب و یک خط هادی عمود بر محور قطبی تعریف کنیم.
اگر $$F$$ یک نقطه ثابت (کانون) باشد و $$D$$ یک خط ثابت (هادی)، در این صورت $$e$$ یک عدد مثبت ثابت به نام خروج از مرکز (Eccentricity) است که میتوانیم به عنوان نسبت فاصلهها از یک نقطه روی نمودار نسبت به کانون و نقطه روی منحنی نسبت به هادی تعریف کنیم. در نتیجه، مجموعهای از تمام نقاط $$P$$ به صورت $$e=\dfrac{PF}{PD}$$ مقطع مخروطی است. به عبارت دیگر، میتوانیم مخروطی را به عنوان مجموعه تمام نقاط $$P$$ با این خاصیت تعریف کنیم که نسبت فاصله از $$P$$ به $$F$$ به فاصله از $$P$$ تا $$D$$ برابر با ثابت $$e$$ است.
برای یک مخروط با خروج از مرکز $$ e $$، گزارههای زیر را خواهیم داشت:
- اگر $$0≤e<1 $$ باشد، مقطع مخروطی یک بیضی است.
- اگر $$ e = 1 $$ باشد، مقطع مخروطی یک سهمی است.
- اگر $$ e > 1$$ باشد، مقطع مخروطی یک هذلولی است.
با این تعریف، اکنون میتوانیم مخروطی را بر حسب هادی $$x=\pm p$$، خروج از مرکز $$e$$ و زاویه $$\theta$$ تعریف کنیم. بنابراین، هر مخروط را میتوان به صورت یک معادله قطبی، یعنی معادلهای برحسب $$r$$ و $$\theta$$ نوشت.
معادله قطبی یک مقطع مخروطی
برای یک مقطع مخروطی با کانون در مبدأ، اگر هادی $$x=\pm p$$ باشد، که در آن، $$p$$ یک عدد حقیقی مثبت است و خروج از مرکز عدد حقیقی مثبت $$e$$ باشد، معادله قطبی آن به صورت زیر خواهد بود:
$$ \large r = \dfrac { e p } { 1 \pm e \cos \theta } $$
برای مقطع مخروطی با کانون در مبدأ، اگر هادی $$y=\pm p$$ باشد، که در آن $$p$$ یک عدد حقیقی مثبت است و خروج از مرکز عدد حقیقی مثبت $$e$$ است، معادله قطبی به شکل زیر خواهد بود:
$$ \large r = \dfrac { e p } { 1 \pm e \sin \theta } $$
اما چگونه میتوانیم با داشتن معادله قطبی یک مقطع مخروطی، نوع آن، هادی و کانون را مشخص کنیم؟ برای این کار کافی است مراحل زیر را انجام دهیم:
- صورت و مخرج را در وارون عدد ثابت مخرج ضرب میکنیم تا معادله را به شكل استاندارد بازنويسی کنیم.
- خروج از مرکز $$ e $$ ضریب تابع مثلثاتی مخرج است. آن را مشخص میکنیم.
- $$ e $$ را با $$ 1 $$ مقایسه میکنیم تا شکل و نوع مخروطی مشخص شود.
- اگر کسینوس در مخرج باشد، هادی $$ x = p $$ است و اگر سینوس در مخرج باشد، هادی $$ y =p $$ خواهد بود. $$ e p $$ را برابر با صورت فرم استاندارد قرار میدهیم تا آن را برای $$ x $$ یا $$ y $$ حل کنیم.
مثالی از مشخص کردن یک مقطع مخروطی به فرم قطبی
برای هر یک از معادلههای زیر، مخروط را با کانون در مبدأ، هادی و خروج از مرکز مشخص کنید.
(الف) $$r = \dfrac { 6 } { 3 + 2 \sin \theta } $$
(ب) $$ r = \dfrac { 1 2 } { 4 + 5 \cos \theta } $$
(ج) $$ r = \dfrac { 7 } { 2 − 2 \sin \theta } $$
برای هر یک از سه مقطع مخروطی، معادله را به شکل استاندارد بازنویسی میکنیم. فرم استاندارد دارای عدد $$1$$ به عنوان ثابت در مخرج است. بنابراین، در هر سه بخش، اولین قدم ضرب کردن صورت و مخرج در وارون ضریب معادله اصلی، یعنی $$\dfrac{1}{c}$$ است، که در آن، $$ c $$ آن ثابت مورد نظر است.
حل (الف): صورت و مخرج را در $$\dfrac{1}{3} $$ ضرب میکنیم.
$$ \large r = \dfrac { 6 } { 3 + 2 \sin \theta } ⋅ \dfrac { \left ( \dfrac { 1 } { 3 } \right ) } { \left ( \dfrac { 1 } { 3 } \right ) } = \dfrac { 6 \left ( \dfrac { 1 } { 3 } \right ) } { 3 \left ( \dfrac { 1 } { 3 } \right ) + 2 \left ( \dfrac { 1 } { 3 } \right ) \sin \theta } = \dfrac { 2 } { 1 + \dfrac { 2 } { 3 } \sin \theta } $$
از آنجا که $$\sin \theta$$ در مخرج است، هادی $$ y = p $$ خواهد بود. با مقایسه نسبت به فرم استاندارد، $$e=\dfrac{2}{3} $$ را خواهیم داشت. بنابراین، داریم:
$$ \large \begin {align*} 2 & = e p \\ 2 & = \dfrac { 2 } { 3 } p \\ \left ( \dfrac { 3 } { 2 } \right ) 2 & = \left ( \dfrac { 3 } { 2 } \right ) \dfrac { 2 } { 3 } p \\ 3 & = p \end {align*} $$
از آنجا که $$e<1$$، مقطع مخروطی یک بیضی است. خروج از مرکز $$e=\dfrac{2}{3} $$ و هادی $$ y = 3 $$ است.
حل (ب): صورت و مخرج را در $$\dfrac{1}{4} $$ ضرب میکنیم.
$$ \large \begin {align*} r & = \dfrac { 1 2 } { 4 + 5 \cos \theta } \cdot \dfrac { \left ( \dfrac { 1 } { 4 } \right ) }{ \left ( \dfrac { 1 } { 4 } \right ) } \\ r & = \dfrac { 1 2 \left ( \dfrac { 1 } { 4 } \right ) } { 4 \left ( \dfrac { 1 } { 4 } \right ) + 5 \left ( \dfrac { 1} { 4 } \right ) \cos \theta } \\ r & = \dfrac { 3 }{ 1 + \dfrac { 5 } { 4 } \cos \theta } \end {align*} $$
از آنجا که $$\cos \theta$$ در مخرج است، هادی $$ x = p $$ خواهد بود. با مقایسه با فرم استاندارد، $$e=\dfrac{5}{4} $$ را داریم. بنابراین، با توجه به صورت، خواهیم داشت:
$$ \large \begin {align*} 3 & = e p \\ 3 & = \dfrac { 5 } { 4 } p \\ \left ( \dfrac { 4 } { 5 } \right ) 3 & = \left ( \dfrac { 4 } { 5 } \right ) \dfrac { 5 } { 4 } p \\ \dfrac { 1 2 } { 5 } & = p \end {align*} $$
از آنجا که $$ e>1 $$، مقطع مخروطی یک هذلولی است. خروج از مرکز و هادی نیز، به ترتیب، $$ e=\dfrac{5}{4} $$ و $$x=\dfrac{12}{5}=2.4 $$ هستند.
حل (ج): صورت و مخرج را در $$\dfrac{1}{2} $$ ضرب میکنیم:
$$ \large \begin {align*} r & = \dfrac { 7 } { 2 - 2 \sin \theta } \cdot \dfrac { \left ( \dfrac { 1 } { 2 } \right ) } { \left ( \dfrac { 1 } { 2 } \right ) } \\ r & = \dfrac { 7 \left ( \dfrac { 1 }{ 2 } \right ) } { 2 \left ( \dfrac { 1 } { 2 } \right ) - 2 \left ( \dfrac { 1 } { 2 } \right ) \sin \theta } \\ r & = \dfrac { \dfrac { 7 } { 2 }} { 1 - \sin \theta } \end {align*} $$
از آنجا که در مخرج سینوس داریم، هادی $$ y = - p $$ خواهد بود. در مقایسه با فرم استاندارد، $$ e = 1 $$ را خواهیم داشت. بنابراین، صورت به شکل زیر خواهد بود:
$$ \large \begin {align*} \dfrac { 7 } { 2 } & = e p \\ \dfrac { 7 } { 2 } & = ( 1 ) p \\ \dfrac { 7 } { 2 } & = p \end {align*}$$
از آنجا که $$ e=1$$، مقطع مخروطی یک سهمی است. خروج از مرکز نیز $$ e = 1 $$ و هادی آن $$y=−\dfrac{7}{2}=−3.5 $$ است.
نمودار معادلات قطبی مقاطع مخروطی
هنگام رسم نمودار در مختصات دکارتی، هر مقطع مخروطی یک معادله منحصر به فرد دارد. این مورد در هنگام رسم نمودار در مختصات قطبی اتفاق نمیافتد. برای تعیین اینکه کدام نوع منحنی را رسم کنیم، باید از خروج از مرکز مخروط استفاده کنیم تا نوع مقطع مخروطی تعیین شود و سپس مشخصههای خاص آن را تعیین کنیم.
گام اول، بازنویسی مقطع مخروطی به شکل استاندارد است که در بخش قبل با آن آشنا شدیم. به عبارت دیگر، باید معادله را بازنویسی کنیم تا مخرج با 1 شروع شود. با این کار قادر خواهیم بود $$ e $$ و در نتیجه، شکل منحنی را تعیین کنیم. گام بعدی جایگذاری مقادیر $$ \theta $$ و حل معادله برای $$ r $$ است تا منحنی رسم شود. با قرار دادن $$ \theta $$ برابر با $$ $$، $$ \dfrac{\pi}{2}$$، $$ \pi$$ و $$\dfrac{3\pi}{2}$$ رئوس به دست میآیند و طرح خام نمودار حاصل میشود.
مثالی از رسم نمودار سهمی در مختصات قطبی
نمودار $$ r=\dfrac{5}{3+3 \cos \theta} $$ را رسم کنید.
حل: ابتدا مقطع مخروطی را با ضرب وارون $$3$$، یعنی $$ \frac 13 $$، در صورت و مخرج، به فرم استاندارد بازنویسی میکنیم:
$$ \large \begin {align*} r & = \dfrac { 5 } { 3 + 3 \cos \theta } = \dfrac { 5 \left ( \dfrac { 1 } { 3 } \right ) } { 3 \left ( \dfrac { 1 } { 3 } \right ) + 3 \left ( \dfrac { 1 } { 3 } \right ) \cos \theta } \\ r & = \dfrac { \dfrac { 5 } { 3 } } { 1 + \cos \theta } \end {align*} $$
از آنجا که $$ e = 1 $$ است، نمودار یک سهمی با مرکز مبدأ است. تابع یک $$ \cos \theta $$ دارد و دارای یک علامت مثبت در مخرج نیز هست، بنابراین، هادی $$ x = p $$ خواهد بود.
$$ \large \begin {align*} \dfrac { 5 } { 3 } & = e p \\ \dfrac { 5 } { 3 } & = ( 1 ) p \\ \dfrac { 5 } { 3 } & = p \end {align*} $$
هادی $$ x=\dfrac{5}{3} $$ است.
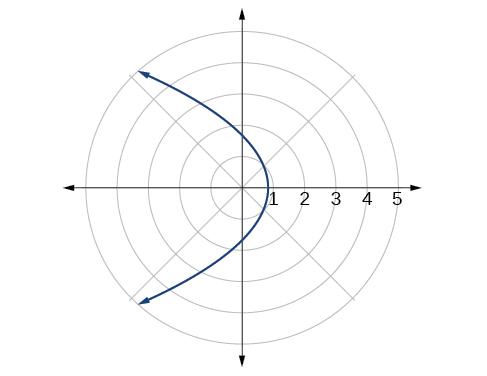
چند نقطه در جدول زیر آورده شدهاند. شکل ۳ نمودار منحنی را نشان میدهد.
| $$ D $$ | $$ C $$ | $$ B $$ | $$ A $$ | |
| $$\dfrac{3\pi}{2}$$ | $$\pi$$ | $$\dfrac{\pi}{2}$$ | $$0$$ | $$\theta$$ |
| $$\dfrac{5}{3}≈1.67$$ | تعریف نشده | $$\dfrac{5}{3}≈1.67$$ | $$\dfrac{5}{6}≈0.83$$ | $$r=\dfrac{5}{3+3 \cos \theta}$$ |
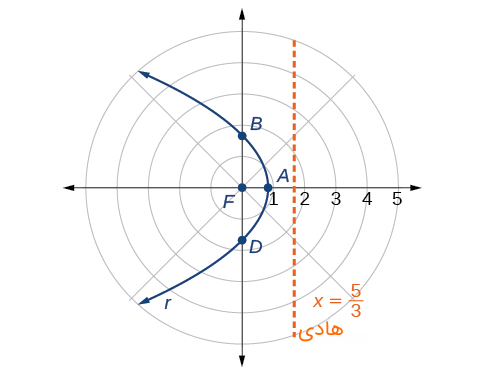
شکل بالا را میتوانیم با نتیجه رسم معادله در یک نرمافزار مقایسه کنیم. شکل ۴ این مورد را نشان میدهد.
مثالی از نمودار هذلولی در مختصات قطبی
نمودار $$r=\dfrac{8}{2−3 \sin \theta} $$ را رسم کنید.
حل: ابتدا مقطع مخروطی را با ضرب وارون $$2$$، یعنی $$ \frac 12 $$، در صورت و مخرج، به فرم استاندارد بازنویسی میکنیم:
$$ \large \begin {align*} r & = \dfrac { 8 } { 2 − 3 \sin \theta } = \dfrac { 8 \left ( \dfrac { 1 } { 2 } \right ) } { 2 \left ( \dfrac { 1 } { 2 } \right ) − 3 \left ( \dfrac { 1 } { 2 } \right ) \sin \theta } \\ r & = \dfrac { 4 } { 1 − \dfrac { 3 } { 2 } \sin \theta } \end {align*} $$
از آنجا که $$ e=\dfrac{3}{2} $$ و بزرگتر از ۱ است، یک هذلولی با کانون مبدأ خواهیم داشت. تابع یک جمله $$ \sin \theta $$ دارد و یک علامت منفی در مخرج وجود دارد، در نتیجه، هادی $$ y = - p $$ خواهد بود.
$$ \large \begin {align*} 4 & = e p \\ 4 & = \left ( \dfrac { 3 }{ 2 } \right ) p \\ 4 \left ( \dfrac { 2 } { 3 } \right ) & = p \\ \dfrac { 8 } { 3 } & = p \end {align*} $$
هادی $$ y=−\dfrac{8}{3} $$ است.
چند نقطه در جدول زیر آورده شدهاند. شکل ۵ نمودار منحنی را نشان میدهد.
| $$ D $$ | $$ C $$ | $$ B $$ | $$ A $$ | |
| $$\dfrac{3\pi}{2}$$ | $$\pi$$ | $$\dfrac{\pi}{2}$$ | $$0$$ | $$\theta$$ |
| $$\dfrac{8}{5}=1.6$$ | $$4$$ | $$−8$$ | $$4$$ | $$r=\dfrac{8}{2−3\sin \theta}$$ |
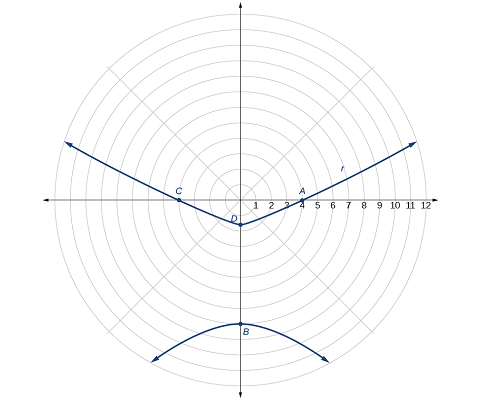
مثالی از رسم نمودار بیضی در مختصات قطبی
نمودار $$r=\dfrac{10}{5−4 \cos \theta}$$ را رسم کنید.
حل: ابتدا مقطع مخروطی را با ضرب وارون $$5$$، یعنی $$ \frac 15 $$، در صورت و مخرج، به فرم استاندارد بازنویسی میکنیم:
$$ \large \begin {align*} r & = \dfrac { 1 0 } { 5 − 4 \cos \theta } = \dfrac { 1 0 \left ( \dfrac { 1 } { 5 } \right ) } { 5 \left ( \dfrac { 1 } { 5 } \right ) − 4 \left ( \dfrac { 1 } { 5 } \right ) \cos \theta } \\ r & = \dfrac { 2 } { 1 − \dfrac { 4 } { 5 } \cos \theta } \end {align*} $$
از آنجا که $$e=\dfrac{4}{5}$$ است، $$ e < 1 $$ خواهد بود، بنابراین، یک بیضی با کانون در مبدأ رسم خواهیم کرد. تابع دارای یک $$ \cos \theta $$ است و یک علامت منفی در مخرج وجود دارد، بنابراین، هادی $$ x = - p $$ است.
$$ \large \begin {align*} 2 & = e p \\ 2 & = \left ( \dfrac { 4 }{ 5 } \right ) p \\ 2 \left ( \dfrac { 5 } { 4 } \right ) & = p \\ \dfrac { 5 } { 2 } & = p \end {align*} $$
در نتیجه، هادی $$x=−\dfrac{5}{2}$$ خواهد بود.
چند نقطه در جدول زیر آورده شدهاند. شکل ۶ نمودار منحنی را نشان میدهد.
| $$D$$ | $$C$$ | $$B$$ | $$A$$ | |
| $$\dfrac{3\pi}{2}$$ | $$\pi$$ | $$\dfrac{\pi}{2}$$ | $$0$$ | $$\theta$$ |
| $$2$$ | $$\dfrac{10}{9}≈1.1$$ | $$2$$ | $$10$$ | $$r=\dfrac{10}{5−4 \cos \theta}$$ |
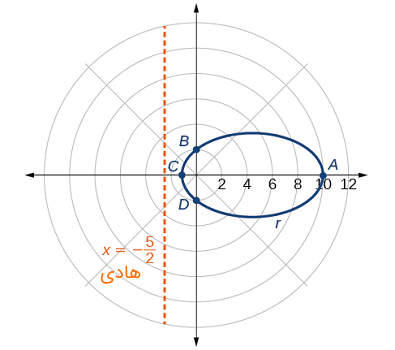
میتوانیم نتیجه را با استفاده از یک نرمافز رایانهای مقایسه کنیم که در شکل ۷ نشان داده شده است.
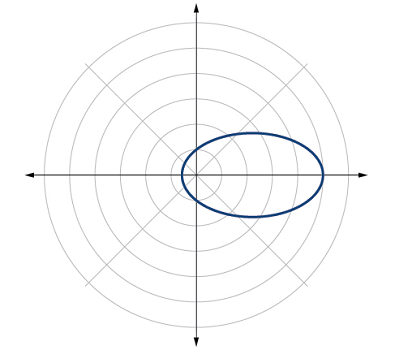
تعریف مقاطع مخروطی برحسب یک کانون و یک هادی
تاکنون از معادلات قطبی مقاطع مخروطی برای توصیف و رسم نمودار منحنی آنها استفاده کردیم. اکنون برعکس کار خواهیم کرد. بدین معنی که معادله قطبی را از اطلاعاتی در مورد مبدأ، خروج از مرکز و هادی به دست خواهیم آورد.
این کار را به صورت زیر انجام خواهیم داد:
- افقی یا عمودی بودن هادی را تعیین میکنیم. اگر هادی برحسب $$ y $$ باشد، از فرم قطبی عمومی برحسب سینوس استفاده میکنیم. اگر هادی برحسب $$x$$ باشد، از فرم قطبی عمومی برحسب کسینوس استفاده خواهیم کرد.
- علامت مخرج را تعیین میکنیم. اگر $$ p < 1 $$ باشد، از علامت منفی و اگر $$ p > 0 $$ باشد، از علامت مثبت استفاده میکنیم.
- ضریب تابع مثلثاتی را به عنوان خروج از مرکز در نظر میگیریم.
- قدر مطلق $$p$$ را در صورت مینویسیم و معادله را ساده میکنیم.
مثالی اول مقاطع مخروطی برحسب یک کانون و یک هادی
فرم قطبی یک مقطع مخروطی با کانون در مبدأ، $$ e = 3 $$ و هادی $$ y = - 2 $$ را به دست آورید.
حل: هادی $$ y = - p $$ است، بنابراین، در مییابیم که تابع مثلثاتی مخرج سینوس است.
از آنجا که $$ y = - 2 $$ و $$ - 2 < 0 $$ است، میدانیم یک علامت منفی در مخرج خواهیم داشت. از فرم استاندارد زیر استفاده میکنیم:
$$ \large r = \dfrac { e p } { 1 − e \sin \theta } $$
و $$e=3$$ و $$|−2|=2=p$$.
بنابراین:
$$ \large \begin {align*} r & = \dfrac { ( 3 ) ( 2 ) } { 1 - 3 \sin \theta } \\ r & = \dfrac { 6 } { 1 - 3 \sin \theta } \end {align*} $$
مثالی دوم مقاطع مخروطی برحسب یک کانون و یک هادی
فرم قطبی یک مقطع مخروطی با کانون مبدأ، $$e=\dfrac{3}{5}$$ و هادی $$ x = 4 $$ را بیابید.
حل: از آنجا که هادی $$ x = p $$ است، میدانیم که تابع مخرج کسینوس خواهد بود. از آنجا که $$ x = 4 $$ بوده و $$ 4 > 0 $$ است نیز یک علامت مثبت در مخرج وجود دارد. از فرم استاندارد زیر استفاده میکنیم:
$$ \large r = \dfrac { e p } { 1 + e \cos \theta } $$
که $$e=\dfrac{3}{5}$$ و $$|4|=4=p $$ است.
بنابراین، داریم:
$$ \large \begin {align*} r & = \dfrac { \left ( \dfrac { 3 } { 5 } \right ) ( 4 ) } { 1 + \dfrac { 3 } { 5 } \cos \theta } \\ r & = \dfrac { \dfrac { 1 2 } { 5 } } { 1 + \dfrac { 3 } { 5 } \cos \theta } \\ r & = \dfrac { \dfrac { 1 2 } { 5 } } { 1 \left ( \dfrac { 5 } { 5 } \right ) + \dfrac { 3 } { 5 } \cos \theta } \\ r & = \dfrac { \dfrac { 1 2 } { 5 } } { \dfrac { 5 } { 5 } + \dfrac { 3 } { 5 } \cos \theta } \\ r & = \dfrac { 1 2 } { 5 } ⋅\dfrac { 5 } { 5 + 3 \cos \theta} \\ r & = \dfrac { 1 2 } { 5 + 3 \cos \theta } \end {align*} $$
مثال تبدیل فرم قطبی مقطع مخروطی به فرم دکارتی
مقطع مخروطی $$r=\dfrac{1}{5−5\sin \theta}$$ را به فرم دکارتی تبدیل کنید.
حل: با استفاد از اتحاد $$r=\sqrt{x^2+y^2}$$ که در آن، $$x=r \cos \theta$$ و $$y=r \sin \theta$$ است، فرمول را بازنویسی میکنیم:
$$ \large \begin {align*} r & = \dfrac { 1 } { 5 - 5 \sin \theta } \\ r \cdot ( 5 - 5 \sin \theta ) & = \dfrac { 1 } { 5 - 5 \sin \theta } \cdot ( 5 - 5 \sin \theta ) \\ 5 r - 5 r \sin \theta & = 1 \\ 5 r & = 1 + 5 r \sin \theta \\ 2 5 r ^ 2 & = { ( 1 + 5 r \sin \theta ) } ^ 2 \\ 2 5 ( x ^ 2 + y ^ 2 ) & = { ( 1 + 5 y ) } ^ 2 \\ 2 5 x ^ 2 + 2 5 y ^ 2 & = 1 + 1 0 y + 2 5 y ^ 2 \qquad \\ 2 5 x ^ 2 - 1 0 y & = 1 \end {align*} $$











سلام طریقه رسم مارپیچ های ارشمیدسی و هذلولوی با معادله ی r= تتا وتتا/ r=1
را بیزحمت برام توضیح بدهید و برای پیدا کردن مساحت زیر خم اینها چگونه حدود را پیدا میکنیم
سلام. احتمالاً آموزشهای زیر به شما کمک خواهند کرد:
مشتق در مختصات قطبی — به زبان ساده (+ دانلود فیلم آموزش رایگان)
مساحت در مختصات قطبی — به زبان ساده (+ دانلود فیلم آموزش رایگان)
سالم و موفق باشید.