محاسبه حجم — به زبان ساده (+ فیلم آموزش رایگان)

حجم یک شکل، معادل با فضایی در نظر گرفته میشود که توسط آن اشغال میشود. از این رو محاسبه حجم در بسیاری از مفاهیم مرتبط با ریاضی و فیزیک دیده میشود. بنابراین در این مطلب از مجله فرادرس قصد داریم تا نحوه محاسبه حجم چندین شکل هندسی مختلف را توضیح دهیم.
محاسبه حجم
حجم به صورت فضایی در نظر گرفته میشود که میتوان در آن هوا، آب یا جرم خاصی قرار داد. معمولا واحدهای اندازهگیری حجم برابر با سانتیمتر مکعب ()، متر مکعب ، اینچ مکعب () یا فوت مکعب () است.
محاسبه حجم مکعب
مکعب، شکلی سهبعدی محسوب میشود که از ۶ وجه برابر تشکیل شده است. در شکل زیر یک مکعب با طول وجوه نشان داده شده است.
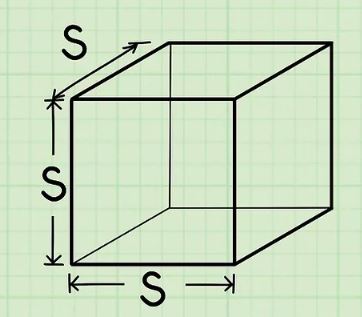
برای نمونه یک حبه قند را میتوان به عنوان مکعب در نظر گرفت. برای بدست آوردن حجم مکعب، کافی است هریک از ابعاد آن در یکدیگر ضرب شوند. با توجه به برابر بودن اضلاع، کافی است یکی از طولها را به توان ۳ رساند. برای نمونه مکعبی را در نظر بگیرید که اندازه ضلع آن برابر با باشد. در این صورت حجم این مکعب برابر با است.
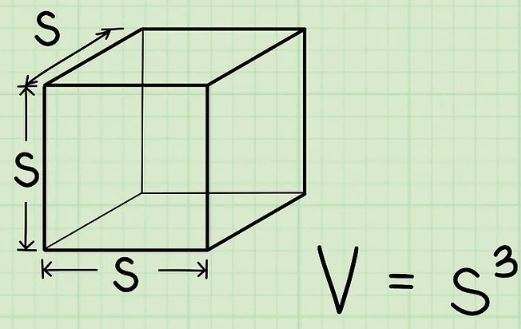
توجه داشته باشید که در مواردی ممکن است حجم مکعب از شما خواسته شود و تنها یک ضلع از آن داده شده باشد. در این موارد باید طول مابقی اضلاع نیز برابر با طول داده شده در نظر گرفته شوند. برای نمونه مکعبی را در نظر بگیرید که طول یکی از اضلاع آنها برابر با باشد. در این صورت اندازه حجم چنین مکعبی برابر است با:
توجه داشته باشید که واحدها نیز همچون اعداد، در یکدیگر ضرب میشوند. بنابراین واحد حجم بدست آمده در بالا برابر است با:
محاسبه حجم مکعب مستطیل
مکعب مستطیل، شکلی است که دارای ۶ وجه است. اما وجههای این جسم اندازههای متفاوتی دارند. در حقیقت یک مکعب مستطیل از طول، عرض و ارتفاع تشکیل شده است.
البته توجه داشته باشید که مکعب، زیرمجموعهای از مکعب مستطیل محسوب میشود. در شکل زیر یک مکعب مستطیل به همراه طول ()، عرض () و ارتفاع () آن نشان داده شده است.
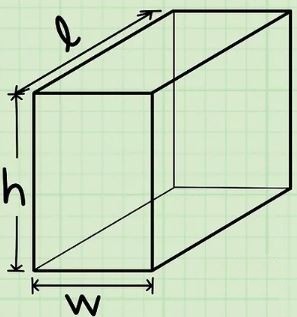
برای بدست آوردن حجم یک مکعب مستطیل کافی است، طول، عرض و ارتفاع آن را در هم ضرب کرد.
معمولا طول، برابر با بزرگترین ضلع موجود در مکعب مستطیل در نظر گرفته شده و موازی با سطح زمین است. برای مکعب مستطیلِ زیر، اندازه طول نشان داده شده است ().
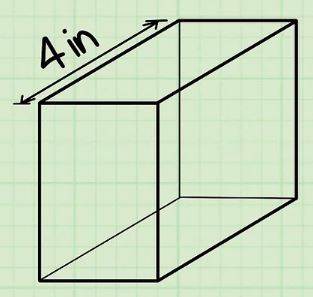
در مورد تشخیص طول، عرض یا ارتفاع در یک مکعب مستطیل نگران نباشید؛ چراکه اندازه حجم با جابجا فرض شدن آنها، تفاوتی نخواهد داشت. بر خلاف طول، عرض را معمولا برابر با کوتاهترین طول مکعب مستطیل در نظر میگیرند که موازی با سطح زمین است. در شکل زیر عرض مکعب مستطیل فرضی نیز نشان داده شده است ().
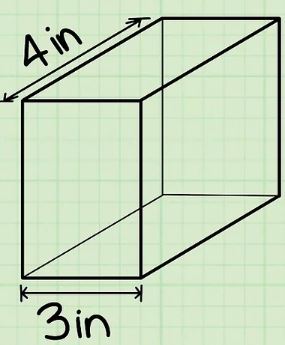
ارتفاع را برابر با فاصله زمین تا سطح قرار گرفته در بالای مکعب مستطیل در نظر بگیرید. برای نمونه ارتفاعِ مکعب مستطیل زیر برابر با است.
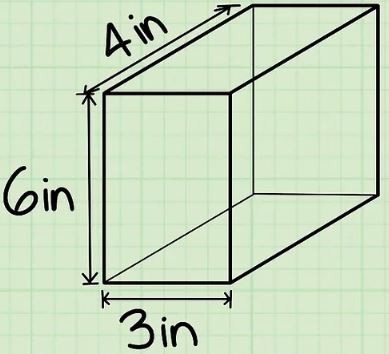
حال فرض کنید میخواهیم حجم مکعب مستطیل فوق را بدست آوریم. همانطور که در بالا نیز بیان شد، برای بدست آوردن حجم باید طول، عرض و ارتفاع را در هم ضرب کرد. بنابراین این مستطیل برابر است با:
بدیهی است که با ضرب کردن واحد طولها در هم، واحد حجم بدست میآید. بنابراین اندازه حجم و واحد آن برابر است با:
محاسبه حجم استوانه
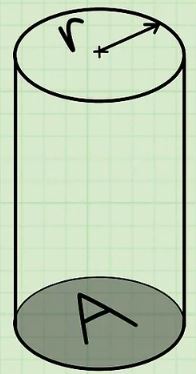
استوانه به شکلی گفته میشود که از یک شکل لولهای مانند به همراه دو سطح دایرهای صاف تشکیل شده است. یک استوانه دو مشخصه اصلی تحت عنوان شعاع () و ارتفاع () دارد. قاعده، صفحاتی هستند که در بالا و پایین استوانه قرار گرفتهاند. این دو صفحه تحت عنوان قاعده شناخته میشوند. یک باتری قلمی یا تنه درخت را میتوان به عنوان استوانه در نظر گرفت. در شکل زیر، استوانه به همراه شعاع و ارتفاع آن نشان داده شدهاند.
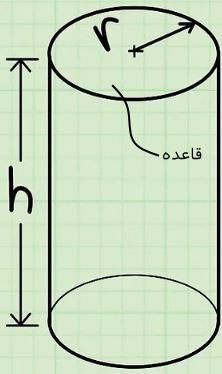
برای بدست آوردن حجم یک استوانه به دو مشخصه شعاع و ارتفاع نیاز است. حال فرض کنید شعاع و ارتفاع استوانهای به ترتیب برابر با و باشند. در این صورت اندازه حجم استوانه برابر است با:
توجه داشته باشید که نشاندهنده مساحت قاعده استوانه بوده که با ضرب شدن آن در ارتفاع، حجم بدست میآید. در مواردی ممکن است به جای شعاعِ ، قطرِ داده شده باشد. در این صورت در ابتدا باید قطر را به ۲ تقسیم کرده سپس از آن به منظور محاسبه حجم استفاده کرد.
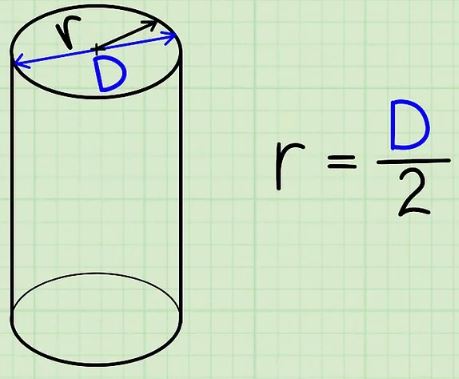
حال فرض کنید حجم استوانهای از شما خواسته شده، اما به جای شعاع ()، به شما محیط دایره () داده شده است. در شکل زیر محیط قاعده به رنگ قرمز نشان داده شده است.
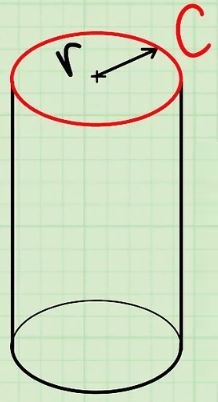
در این شرایط با تقسیم کردن به عدد اندازه شعاع بدست آمده و سپس با قرار دادن شعاع در رابطه ، اندازه حجم بدست خواهد آمد. برای نمونه فرض کنید شعاع استوانهای برابر با است. در این صورت در ابتدا مساحت مقطع نشان داده شده در شکل زیر برابر میشود با:
حال برای بدست آوردن حجم کافی است تا مساحت بدست آمده را در ارتفاع ضرب کرد. با انجام این کار اندازه حجم برابر میشود با:
محاسبه حجم هِرم
هرم به شکلی در هندسه گفته میشود که قاعده آن به صورت یک چندضلعی باشد. همچنین این شکل از وجوه جانبی تشکیل شده که در نقطهای مشخص به هم میرسند. معمولا در ریاضیات از هرمهایی استفاده میشود که قاعده آن یک مستطیل یا مربع باشد.
توجه داشته باشید که قاعده یک هرم میتواند هرچند ضلعی داشته باشد. در شکل زیر یک هرم با قاعدهای مربعی نشان داده شده است. مساحت قاعده آن برابر با و ارتفاع آن نیز برابر با است.
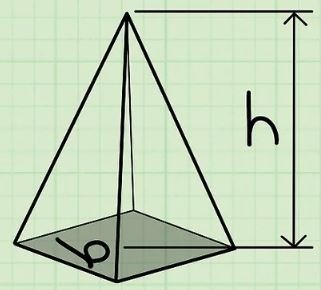
به منظور محاسبه حجم هرم با مساحت قاعده و ارتفاع از رابطه زیر استفاده میشود.
توجه داشته باشید که در اکثر موارد مساحت قاعده هرم را باید در ابتدا محاسبه کرده، سپس حجم را بدست آورد. برای نمونه مطابق با شکل زیر هرمی را در نظر بگیرید که مقطع آن نیز به صورت مربعی با طول است. در این صورت مساحت قاعده آن برابر است با:
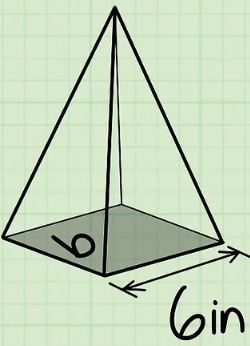
با فرض اینکه ارتفاع این هرم برابر با باشد، اندازه حجم هرم برابر میشود با:
محاسبه حجم مخروط
مخروط شکلی سهبعدی است که قاعده آن به صورت دایرهای است. هر مخروط دو مشخصه ارتفاع () و شعاع قاعده () دارد. در شکل زیر مخروط، شعاع و ارتفاع آن نشان داده شده است.
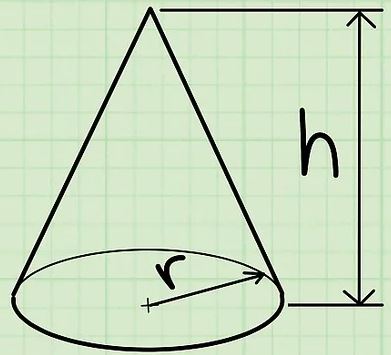
حجم مخروطی به شعاع قاعده () و ارتفاع برابر است با:
برای نمونه مخروطی با شعاعِ و ارتفاع را در نظر بگیرید. حجم این مخروط برابر است با:
با بدست آمدن مساحت قاعده، در مرحله بعد اندازه حجم برابر میشود با:
محاسبه حجم کره
کره به مجموعه نقاطی از فضا گفته میشود که فاصله آنها از نقطه ثابتی، مقداری یکسان باشد.
برای نمونه شکل حبابهای صابون به صورت کره هستند.

به منظور ترسیم یک کره، تنها به یک نقطه ثابت و فاصله نیاز داریم. در این صورت کرهای به شعاع ، با مرکز قابل ترسیم است. در شکل زیر چنین کرهای نشان داده شده است.
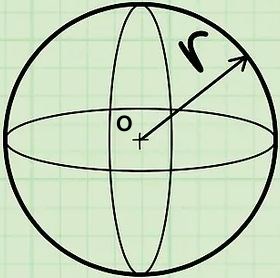
رابطه کلی به منظور محاسبه حجم کرهای به شعاع برابر است با:
برای نمونه حجم اشغالشده توسط کرهای به شعاع برابر است با:
همانطور که مشاهده میکنید در این حالت نیز واحدها در یکدیگر ضرب شدهاند. در مطالب آینده، نحوه محاسبه حجمهای پیچیدهتر را توضیح خواهیم داد.













خیلی خیلی عالی دست سازندش درد نکنه
خوب هر شکل فرمول خاص خودشو داره نمیشه گفت همه اشکال یه فرمول داشته باشن
سلام خسته نباشید
یه سوالی داشتم ازتون
قاعده ی کلی یا دستور کلی برای محاسبه ی حجم اجسام چیست؟
لطفا جواب اینو بدین ممنون
عالی بود. کامل یاد گرفتم. ممنون
سلام در قسمت محاسبه مخروطی در انتهای محاسبه حجم بدست آمده در انتها را باید تقسیم بر 3 کرد و شما این کار را نکردید و چرا واحد استوانه را اینچ مکعب در نظر گرفتید ولی در مخروطی و حرم واحد را متر مربع در نظر گرفتید؟
سلام.
اصلاحات لازم انجام شد.
از توجه شما سپاسگزاریم.
عرض سلام وخسته نباشید.شما که زحمت شکل ها و فرمول های ریاضی رو کشیدید چه خوب بود که از علائم عرف نیز استفاده می شد مثلا برای نمایش اندازه ضلع مکعب به جای s از a و برای نمایش اندازه مساحت قاعده به جای b از s استفاده می کردید.دراین صورت هم مطالب استاندارد ارائه می شد و هم در نگاه اول کاربرمتوجه مطلب می شد.مثلا این جانب در مشاهده فرمول (s به توان 3) = s یک لحظه فکر کردم مطالب اشتباه ارائه شده است. با تشکر از توجه شما.