دوران مقاطع مخروطی — از صفر تا صد
همانطور که میدانیم، مقاطع مخروطی زمانی تشکیل میشوند که یک صفحه، به گونهای، بخشی از مجموعه دو مخروط را که در رأس با هم مشترک هستند قطع کند. در این آموزش درباره دوران مقاطع مخروطی بحث خواهیم کرد.
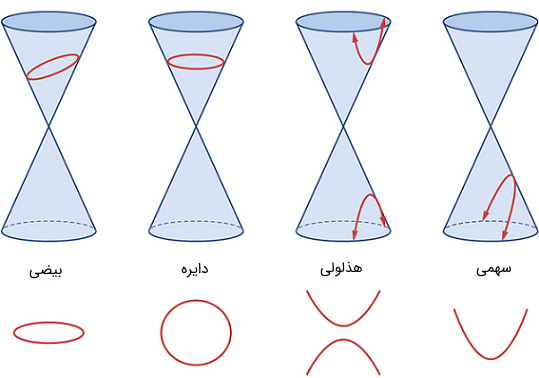
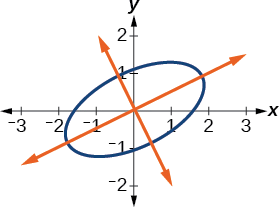
شکل زیر، تشکیل بیضی، دایره، هذلولی و سهمی را به خوبی نشان میدهد.
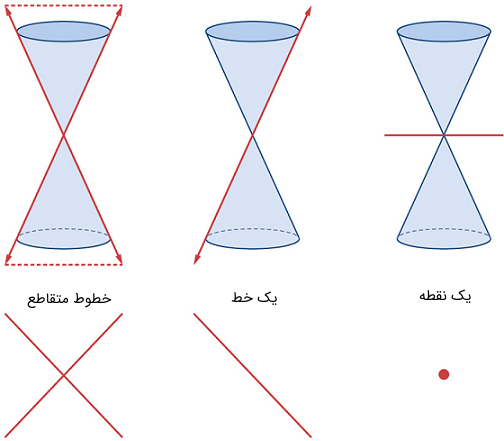
بیضیها، دایرهها، هذلولیها و سهمیها گاهی مقاطع مخروطی ناتباهیده (Nondegenerate) نیز نامیده میشوند تا با مقاطع مخروطی تباهیده (Degenerate) که در شکل ۲ نشان داده شدهاند تمایز داده شوند. یک مقطع مخروطی تباهیده وقتی ایجاد میشود که یک صفحه دو مقطع را در رأس قطع کند. بسته به زاویه صفحه، سه نوع مقطع مخروطی ممکن است ایجاد شود: یک نقطه، یک خط یا دو خط متقاطع.
فرم عمومی مقاطع مخروطی
در آموزشهای قبلی مجله فرادرس، با معادلات مقاطع مخروطی مختلف آشنا شدیم.
در این بخش، معادله عمومی مقاطع مخروطی را ارائه خواهیم کرد که میتوان از آن برای هر مقطع مخروطی استفاده کرد. فرم عمومی، معادلهای برابر با صفر است و جملات و ضرایب مرتبه خاصی دارند:
$$ \large A x ^ 2 + B x y + C y ^ 2 + D x + E y+ F = 0 $$
که در آن، $$A$$، $$B$$ و $$ C $$ نمیتوانند همه با هم صفر باشند. میتوانیم از مقادیر ضرایب برای تعیین نوع مقطع مخروطی مربوط به معادله داده شده استفاده کنیم. احتمالاً این پرسش برایتان ایجاد شده که چرا فرم عمومی بالا دارای جمله $$ x y $$ بوده و در فرم عمومی مقاطعی که تاکنون با آنها آشنا شدهایم وجود نداشته است. همانطور که در ادامه نیز بحث خواهیم کرد، وقتی $$ B $$ صفر نباشد، جمله $$ x y $$ مقطع مخروطی را میچرخاند.
| مقطع مخروطی | مثال |
| بیضی | $$ 4 x ^ 2 + 9 y ^ 2 = 1 $$ |
| دایره | $$ 4 x ^ 2 + 4y ^ 2 = 1 $$ |
| هذلولی | $$ 4 x ^ 2 − 9 y ^ 2 = 1 $$ |
| سهمی | $$ 4 x ^ 2 = 9 y $$ یا $$ 4 y ^ 2 = 9 x $$ |
| یک خط | $$ 4 x + 9 y = 1 $$ |
| دو خط متقاطع | $$ ( x − 4 ) ( y + 4 ) = 0 $$ |
| دو خط موازی | $$ ( x − 4 ) ( x − 9 ) = 0 $$ |
| یک نقطه | $$ 4 x ^ 2 + 4 y ^ 2 = 0 $$ |
| بدون نمودار | $$ 4 x ^ 2 + 4 y ^ 2 = − 1 $$ |
همانطور که گفتیم، فرم عمومی یک مقطع مخروطی به صورت زیر است:
$$ \large A x ^ 2 + B x y + C y ^ 2 + D x + E y + F = 0 \;\;\;\;\; (1) $$
که در آن، $$ A$$، $$ B$$ و $$C$$ نمیتوانند با هم صفر شوند. جدول زیر خلاصهای از مقاطع مخروطی مختلف را نشان میدهد که در آنها، $$ B = 0 $$ و $$ A$$ و $$ C $$ اعداد حقیقی غیرصفر هستند. صفر بودن $$ B $$ یعنی اینکه مقطع مخروطی نچرخیده است.
| بیضی | $$ A x ^ 2 +C y ^ 2 + D x + E y + F = 0 $$، $$ A≠C $$ و $$ AC>0 $$ |
| دایره | $$ Ax^2+Cy^2+Dx+Ey+F=0 $$، $$ A=C $$ |
| هذلولی | $$ Ax^2−Cy^2+Dx+Ey+F=0 $$ یا $$−Ax^2+Cy^2+Dx+Ey+F=0 $$ که در آن، $$ A $$ و $$C$$ مثبت هستند. |
| سهمی | $$ A x ^ 2 + D x + E y + F = 0 $$ یا $$ C y ^ 2 + D x + E y + F = 0 $$ |
تعیین مقطع مخروطی از روی معادله آن
برای تعیین نوع یک مقطع مخروطی از معادله آن، گامهای زیر را طی میکنیم:
۱. بازنویسی معادله به فرم عمومی (۱)؛ یعنی $$ A x ^ 2 + B x y + C y ^ 2 + D x + E y + F = 0 $$.
۲. تعیین مقادیر $$ A $$ و $$C$$ از فرم عمومی:
- اگر $$A$$ و $$C $$ غیرصفر، همعلامت و نابرابر باشند، نمودار ممکن است یک بیضی باشد.
- اگر $$ A $$ و $$ C $$ برابر، غیرصفر و همعلامت باشند، نمودار ممکن است یک دایره باشد.
- اگر $$ A $$ و $$C$$ غیرصفر و دارای علامتهای مخالف باشند، آنگاه نمودار ممکن است یک هذلولی باشد.
- اگر $$ A $$ و $$ C $$ صفر باشند، آنگاه نمودار ممکن است یک سهمی باشد.
اگر $$ B = 0 $$، مقطع مخروطی یک محور عمودی و/یا افقی خواهد داشت. اگر $$ B $$ برابر با صفر نباشد، همانگونه که در ادامه نشان داده شده است، مقطع مخروطی دوران یافته است. در عبارات بالا به عبارت «ممکن است» دقت کنید؛ زیرا شاید بسته به مقادیر $$ A$$، $$ B$$، $$C$$، $$D$$، $$E$$ و $$F$$ معادله در حالت کلی یک مقطع مخروطی را نشان ندهد. برای مثال، وقتی $$A$$ و $$B$$ علامت یکسانی داشته باشند، حالت تباهیده یک دایره یا یک بیضی یک نقطه است:
$$ \large A x ^ 2 + B y ^2 = 0 , \;\;\;\;\; (2) $$
وقتی $$A$$ و $$B$$ علامتهای مخالف هم داشته باشند، حالت تباهیده یک هذلولی دو خط راست متقاطع است: $$ Ax^2+By^2=0$$. در مقابل، وقتی $$ A $$ و $$B$$ مثبت باشند، معادله $$ Ax^2+By^2+1=0 $$ بوده و در حالت کلی نمودار خاصی را نشان نمیدهد، زیرا زوج مرتب حقیقی که در آن صدق کند وجود ندارد.
مثال ۱
نمودار متناظر با هر یک از مقاطع مخروطی ناتباهیده زیر را مشخص کنید.
- الف) $$ 4 x ^ 2 − 9 y ^ 2 + 3 6 x + 3 6y − 1 2 5 = 0 $$
- ب) $$ 9 y ^ 2 + 1 6x + 3 6 y − 1 0 = 0 $$
- ج) $$ 3 x ^ 2 + 3 y ^ 2 − 2 x− 6 y − 4 = 0 $$
- د) $$ − 2 5 x ^ 2 − 4 y ^ 2 + 1 0 0x + 1 6y + 2 0 = 0 $$
حل الف: فرم عمومی (معادله (۱)) را بازنویسی میکنیم:
$$ \large \begin {align*} \color {red} { A } \color {black} x ^ { 2 } + \color {blue} { B } \color {black} x y + \color {red} { C } \color {black} y ^ { 2 } + \color{blue} { D } \color {black} x + \color {blue} { E } \color {black} y + \color {blue} { F } & = 0 \\ 4 x ^ { 2 } + 0 x y + ( - 9 ) y ^ { 2 } + 36 x + 36 y + ( - 1 2 5 ) & = 0 \end {align*} $$
همانطور که میبینیم، $$ A = 4 $$ و $$ C = - 9 $$ است و $$ A$$ و $$C$$ علامتهای مخالف هم دارند. نمودار این معادله یک هذلولی است.
حل ب: فرم عمومی (معادله (۱)) را بازنویسی میکنیم:
$$ \large \begin {align*} \color {red} { A } \color {black} x ^ { 2 } + \color {blue} { B } \color {black} x y + \color {red} { C } \color {black} y ^ { 2 } + \color {blue} { D } \color {black} x + \color {blue} { E } \color {black} y + \color {blue} { F } & = 0 \\[4pt] 0 x ^ { 2 } + 0 x y + 9 y ^ { 2 } + 16 x + 36 y + ( - 1 0 ) & = 0 \end {align*} $$
که در آن، $$ A = 0 $$ و $$ C = 9 $$. از آنجایی که $$ A $$ صفر است، میتوان گفت که این معادله یک سهمی را نشان میدهد.
حل ج: فرم عمومی (معادله (۱)) را بازنویسی میکنیم:
$$ \large \begin {align*} \color {red} { A } \color {black} x ^ { 2 } + \color {blue} { B } \color {black} x y + \color {red} { C } \color {black} y ^ { 2 } + \color {blue} { D } \color {black} x + \color {blue} { E } \color {black} y + \color {blue} { F } & = 0 \\[4pt] 3 x ^ { 2 } + 0 x y + 3 y ^ { 2 } + ( - 2 ) x + ( - 6 ) y + ( - 4 ) & = 0 \end {align*} $$
که در آن، $$ A = 3 $$ و $$ C = 3 $$ است. با توجه به برابر بودن $$ A $$ و $$ C $$، معادله مربوط به یک دایره است.
حل د: فرم عمومی (معادله (۱)) را بازنویسی میکنیم:
$$ \large \begin {align*} \color {red} { A } \color {black} x ^ { 2 } + \color {blue} { B } \color {black} x y + \color {red} { C } \color {black} y ^ { 2 } + \color {blue} { D } \color {black} x + \color {blue} { E } \color {black} y + \color {blue} { F } & = 0 \\[4pt] ( - 2 5 ) x ^ { 2 } + 0 x y + ( - 4 ) y ^ { 2 } + 1 0 0 x + 1 6 y + 2 0 & = 0 \end {align*} $$
همانطور که میبینیم، $$ A = -25 $$ و $$ C = -4 $$ است. از آنجایی که $$ AC> 0 $$ و $$ A \neq C$$، نمودار این معادله یک بیضی است.
دوران مقاطع مخروطی
تاکنون، معادلات مقاطع مخروطی را بدون جملات $$ x y $$ بررسی کردیم که نمودارها را روی محورهای $$ x $$ و $$ y $$ تراز میکرد.
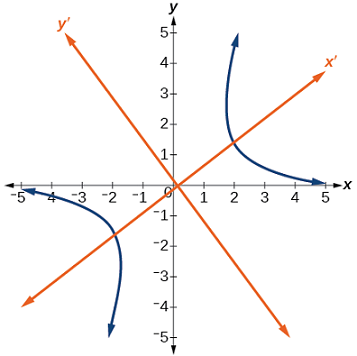
وقتی جمله $$ xy $$ را به معادلات اضافه کنیم، در واقع مقطع مخروطی را حول مبدأ چرخاندهایم. اگر محورهای $$ x $$ و $$ y $$ با زاویه مشخص $$ \theta $$ چرخانده شوند، آنگاه هر نقطه روی صفحه که با زوج مرتب $$ (x, y ) $$ نمایش داده میشود، به نقطه جدید $$(x' , y')$$ منتقل خواهد شد. در این حالت، محورهای جدید $$x'$$ و $$y'$$ هستند (شکل ۳).
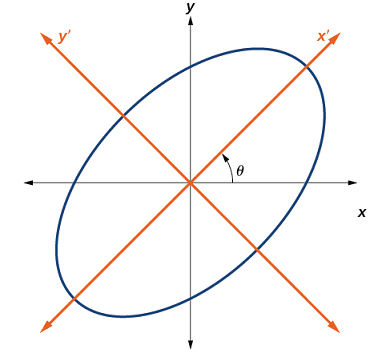
اکنون میخواهیم رابطه بین $$ x $$ و $$y$$ صفحه کارتزین را با $$x'$$ و $$ y'$$ صفحه دوران یافته جدید پیدا کنیم (شکل ۴).
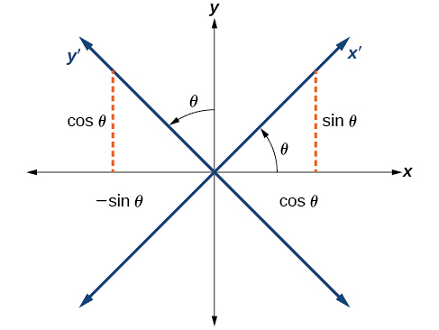
مختصات محورهای $$x$$ و $$ y$$ اولیه دارای بردارهای یکه $$ \hat{i} $$ و $$ \hat{j} $$ هستند. محورهای دوران یافته نیز بردارهای یکه $$ \hat{i}^\prime $$ و $$ \hat{j}^\prime $$ دارند. زاویه $$ \theta $$ به عنوان زاویه دوران شناخته میشود (شکل ۵). میتوانیم بردارهای یکه جدید را بر حسب برادارهای یکه اصلی بنویسیم:
$$ \large \hat { i }′ = \cos \theta \hat { i } + \sin \theta \hat { j } \;\;\;\;\; (3) $$
$$ \large \hat { j }′ = − \sin \theta \hat { i } + \cos \theta \hat { j } \;\;\;\;\; (4) $$
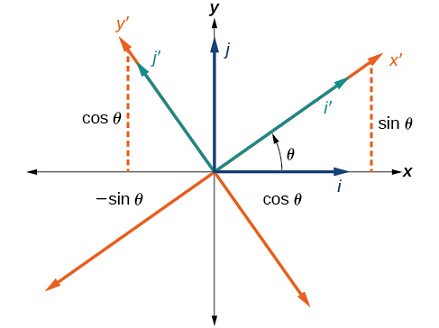
بردار $$ \overrightarrow{u} $$ را در مختصات جدید در نظر بگیرید. این بردار را میتوان برحسب مختصات محورها به صورت زیر نوشت:
$$ \large \begin {align*} \overrightarrow { u } & = x ^ \prime i′ + y ^ \prime j′ \\[4pt] & = x ^ \prime ( i \cos \theta + j \sin \theta ) + y ^ \prime ( − i \sin \theta + j \cos \theta ) \\[4pt] & = i x' \cos \theta + j x' \sin \theta − i y' \sin \theta + j y' \cos \theta \\[4pt] & = i x' \cos \theta − i y' \sin \theta + j x' \sin \theta + j y' \cos \theta \\[4pt] & = ( x' \cos \theta − y' \sin \theta ) i + ( x' \sin \theta + y' \cos \theta ) j \end {align*} $$
از آنجایی که $$ \overrightarrow{u}=x^\prime i′+y^\prime j′ $$، نمایش $$ x $$ و $$ y $$ برحسب دستگاه مختصات جدید به صورت زیر خواهد بود:
$$ \large x = x ^ \prime \cos \theta − y ^ \prime \sin \theta $$
$$ \large y = x ^ \prime \sin \theta + y ^ \prime \cos \theta $$
معادلات دوران
اگر نقطه $$ (x , y )$$ در صفحه کارتزین در یک صفحه مختصات جدید نمایش داده شود، که در آن، محورهای دوران با چرخش به اندازه زاویه $$ \theta $$ نسبت به محور مثبت $$ x $$ شکل گرفتهاند، آنگاه مختصات نقطه نسبت به محورهای جدید $$(x' , y')$$ است. میتوانیم از معادلات دوران زیر برای تعریف رابطه بین $$ (x,y) $$ و $$ (x^\prime , y^\prime ) $$ زیر استفاده کنیم:
$$ \large x = x ^ \prime \cos \theta − y ^ \prime \sin \theta \;\;\;\;\; ( 5 ) $$
و
$$ \large y = x ^ \prime \sin \theta + y ^ \prime \cos \theta \;\;\;\;\; (6 ) $$
برای استخراج معادله مقطع مخروطی پس از دوران، مراحل زیر را طی کنید:
- $$ x $$ و $$ y $$ را پیدا کنید که $$ x=x^\prime \cos \theta−y^\prime \sin \theta $$ و $$ y=x^\prime \sin \theta+y^\prime \cos \theta $$.
- عبارتهای $$ x $$ و $$ y $$ را در معادلات جایگذاری و آنها را ساده کنید.
- معادلات را برای $$ x^\prime $$ و $$ y^\prime $$ به فرم استاندارد بنویسید.
مثال ۲
اگر معادله $$ 2x^2−xy+2y^2−30=0 $$ به اندازه $$ \theta=45° $$ دوران کند، معادله پس از دوران به چه صورت در خواهد آمد؟
حل: مقادیر $$ x $$ و $$ y $$ را محاسبه میکنیم که $$ x=x^\prime \cos \theta−y^\prime \sin \theta $$ و $$ y=x^\prime \sin \theta+y^\prime \cos \theta$$.
از آنجایی که $$ \theta=45° $$، داریم:
$$ \large \begin {align*} x & = x ^ \prime \cos ( 4 5 ° ) − y ^ \prime \sin ( 4 5 ° ) \\[4pt] x & = x ^ \prime \left ( \dfrac { 1 } { \sqrt { 2 } } \right ) − y ^ \prime \left ( \dfrac { 1 } { \sqrt { 2 } } \right) \\[4pt] x & = \dfrac { x ^ \prime − y ^ \prime }{ \sqrt { 2 } } \end {align*} $$
و
$$ \large \begin {align*} y & = x ^ \prime \sin ( 4 5 ° ) + y ^ \prime \cos ( 4 5 ° ) \\[4pt] y & = x ^ \prime \left ( \dfrac { 1 } { \sqrt { 2 } } \right ) + y ^ \prime \left ( \dfrac { 1 } { \sqrt { 2 } } \right) \\[4pt] y & = \dfrac { x ^ \prime + y ^ \prime }{ \sqrt { 2 } } \end {align*} $$
عبارات $$ x=x^\prime \cos\theta−y^\prime \sin\theta $$ و $$ y=x^\prime \sin \theta+y^\prime \cos \theta $$ را در $$ 2x^2−xy+2y^2−30=0 $$ جایگذاری میکنیم:
$$ \large 2 { \left ( \dfrac { x ^ \prime − y ^ \prime }{ \sqrt { 2 } } \right ) } ^ 2 − \left ( \dfrac { x ^ \prime − y ^ \prime }{ \sqrt { 2 } } \right ) \left ( \dfrac { x ^ \prime + y ^\prime }{ \sqrt { 2 } } \right ) + 2 { \left ( \dfrac { x ^ \prime + y ^ \prime }{ \sqrt { 2 } } \right ) } ^ 2 − 3 0 = 0 $$
همچینن آن را ساده میکنیم:
$$ \large \begin {array} {rl} 2 \dfrac { ( x ^ \prime − y ^ \prime ) ( x ^ \prime − y ^ \prime ) } { 2 } − \dfrac { ( x ^ \prime − y ^ \prime ) ( x ^ \prime + y ^ \prime ) }{ 2 } + 2 \dfrac { ( x ^ \prime + y ^ \prime ) ( x ^ \prime + y ^ \prime ) } { 2 } − 3 0 = 0 \\[4pt] { x ^ \prime } ^ 2 − 2 x ^ \prime y ^ \prime + { y ^ \prime } ^ 2 − \dfrac { ( { x ^ \prime } ^ 2 −{ y ^ \prime } ^ 2 ) } { 2 } + { x ^ \prime } ^ 2 + 2 x ^ \prime y ^ \prime + { y ^ \prime } ^ 2 − 3 0 = 0 \\[4pt] 2 { x ^ \prime } ^ 2 + 2 { y ^ \prime } ^ 2 − \dfrac { ( { x ^ \prime } ^ 2 − { y ^ \prime } ^ 2 ) } { 2 } = 3 0 \\[4pt] 2 ( 2 { x ^ \prime } ^ 2 + 2 { y ^ \prime } ^ 2 − \dfrac { ( { x ^ \prime } ^ 2 − { y ^ \prime } ^ 2 ) } { 2 } ) = 2 ( 3 0 ) \\[4pt] 4 { x ^ \prime } ^ 2 + 4 { y ^ \prime } ^ 2 − ( { x ^ \prime } ^ 2− { y ^ \prime } ^ 2 ) = 6 0 \\[4pt] 4 { x ^ \prime } ^ 2 + 4 { y ^ \prime } ^ 2 − { x ^ \prime } ^ 2 + { y ^ \prime } 2 = 6 0 \\[4pt] \dfrac { 3 { x ^ \prime } ^ 2 } { 6 0 } + \dfrac { 5 { y ^ \prime } ^ 2 } { 6 0 } = \dfrac { 6 0 } { 6 0 } \end {array} $$
معادله نهایی را برحسب $$ x^\prime $$ و $$ y^\prime $$ به فرم استاندارد مینویسیم:
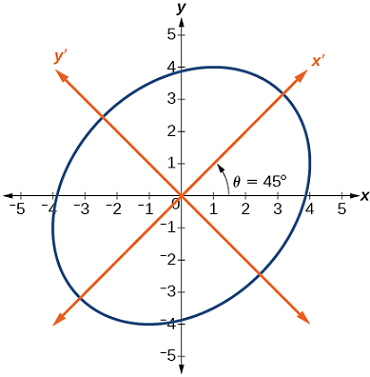
$$ \large \dfrac { { x ^ \prime } ^ 2 } { 2 0 } + \dfrac { { y ^ \prime } ^ 2 } { 1 2 } = 1 \nonumber $$
این معادله یک بیضی را نشان میدهد. نمودار این معادله در شکل ۶ نمایش داده شده است.
فرم استاندارد مخروطیهای دوران یافته
اکنون میتوانیم فرم استاندارد یک مخروطی را که به اندازه زاویه مشخصی چرخیده شده است، به دست آوریم. میخواهیم ببینیم معادله مخروطی به فرم $$ Ax^2+Bxy+Cy^2+Dx+Ey+F=0 $$ با چرخش محورها به چه شکلی در میآید. برای انجام این کار، فرم عمومی را به عنوان یک معادله برای دستگاه مختصات $$ x'$$ و $$y'$$ بدون جمله $$x' y' $$ مینویسیم که با دوران به اندازه $$ \theta$$ در رابطه زیر صدق کند:
$$ \large \cot ( 2 \theta ) = \dfrac { A − C } { B } \;\;\;\;\; (7) $$
قبلاً گفتیم که هر مقطع مخروطی را میتوان با معادله مرتبه دوم زیر نمایش داد:
$$ \large A x ^ 2 + B x y + C y ^ 2 + D x + E y + F = 0 $$
که در آن، $$A$$، $$B $$ و $$ C$$ نمیتوانند با هم صفر باشند. اگر $$ B \neq 0 $$، آنگاه یک جمله $$xy$$ خواهیم داشت که سبب میشود نتوانیم معادله را به فرم استاندارد بازنویسی کنیم. برای رفع این مشکل، میتوانیم محورها را به اندازه زاویه حاده $$ \theta $$ بچرخانیم که در رابطه $$ \cot(2\theta)=\dfrac{A−C}{B} $$ صدق میکند.
- اگر $$ \cot(2\theta)>0 $$، آنگاه $$ 2 \theta $$ در ربع اول بوده و $$ \theta $$ در بازه $$ (0°,45°) $$ قرار دارد.
- اگر $$ \cot(2\theta)<0$$، آنگاه $$ 2 \theta $$ در ربع دوم بوده و $$ \theta $$ در بازه $$(45°,90°)$$ قرار دارد.
- اگر $$ A = C$$، آنگاه $$ \theta=45°$$.
برای نوشتن معادله مقطع مخروطی در دستگاه دوران یافته بدون جمله $$ x'y'$$، گامهای زیر را طی میکنیم:
- یافتن $$ \cot(2\theta) $$.
- یافتن $$ \sin \theta $$ و $$ \cos \theta $$.
- جایگذاری $$ \sin \theta $$ و $$ \cos \theta $$ در $$ x=x^\prime \cos \theta−y^\prime \sin \theta $$ و $$ y=x^\prime \sin \theta+y^\prime \cos \theta $$.
- جایگذاری عبارت $$ x $$ و $$ y $$ در معادله داده شده و سادهسازی آن.
- نوشتن معادلات با $$ x'$$ و $$ y'$$ در فرم استاندارد نسبت به محورهای دوران یافته.
مثال ۳
معادله $$ 8x^2−12xy+17y^2=20 $$ را در دستگاه $$ x^\prime y^\prime $$ بدون جمله $$ x^\prime y^\prime $$ بنویسید.
حل: ابتدا $$ \cot(2\theta) $$ را به دست میآوریم.
$$ \large 8 x ^ 2 − 1 2 x y + 1 7 y ^ 2 = 2 0 \rightarrow A = 8 ,\; B = − 1 2 , \; C = 1 7 $$
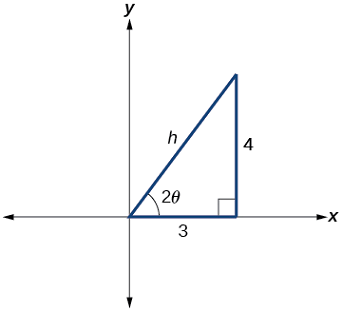
با توجه به شکل ۷، میتوان نوشت:
$$ \large \begin {align*} \cot ( 2 \theta ) & = \dfrac { A − C }{ B } = \dfrac { 8 − 1 7 } { − 1 2 } \\[4pt] & =\dfrac { − 9 }{ − 1 2 } = \dfrac { 3 } { 4} \end {align*} $$
بنابراین، وتر به صورت زیر محاسبه میشود:
$$ \large \begin {align*} 3 ^ 2 + 4 ^ 2 & = h ^ 2 \\[4pt] 9 + 1 6 & = h ^ 2 \\[4pt] 2 5 & = h ^ 2 \\[4pt] h & = 5 \end {align*} $$
در ادامه، $$ \sin \theta $$ و $$ \cos \theta $$ را به دست میآوریم:
$$ \large \begin {align*} \sin \theta & = \sqrt { \dfrac { 1 −\cos ( 2 \theta ) } { 2 } } = \sqrt { \dfrac { 1 − \dfrac { 3 } { 5 } } { 2 } } = \sqrt { \dfrac { \dfrac { 5 } { 5 } − \dfrac { 3 } { 5 } } { 2 } } = \sqrt { \dfrac { 5 − 3 } { 5 } ⋅ \dfrac { 1 }{ 2 } } = \sqrt { \dfrac { 2 } { 1 0 } } = \sqrt { \dfrac { 1 } { 5 } } \\ \sin \theta & = \dfrac { 1 } { \sqrt { 5 } } \\ \cos \theta & = \sqrt { \dfrac { 1 + \cos ( 2 \theta ) }{ 2 } } = \sqrt { \dfrac { 1 + \dfrac { 3 } { 5 } } {2 } } = \sqrt { \dfrac { \dfrac { 5 } { 5 } + \dfrac { 3 } { 5 } } { 2 } } = \sqrt { \dfrac { 5 + 3 } { 5 }⋅ \dfrac { 1 } { 2 } } = \sqrt { \dfrac { 8 } { 1 0 } } = \sqrt { \dfrac { 4 } { 5 } } \\ \cos \theta & = \dfrac { 2 } { \sqrt { 5 } } \end {align*} $$
با جایگذاری مقادیر $$ \sin \theta $$ و $$ \cos \theta $$ در $$ x=x^\prime \cos \theta−y^\prime \sin \theta $$ و $$ y=x^\prime \sin \theta+y^\prime \cos \theta $$، داریم:
$$ \large \begin {align*} x & = x' \cos \theta − y ^ \prime \sin \theta \\[4pt] & = x ^ \prime \left ( \dfrac { 2 } { \sqrt { 5 } } \right ) − y ^ \prime \left ( \dfrac { 1 } { \sqrt { 5 } } \right ) \\[4pt] & = \dfrac { 2 x ^ \prime − y ^ \prime } { \sqrt { 5 } } \end {align*} $$
و
$$ \large \begin {align*} y & = x ^ \prime \sin \theta + y ^ \prime \cos \theta \\[4pt] & = x ^ \prime \left ( \dfrac { 1 } { \sqrt { 5 } } \right ) + y ^ \prime \left ( \dfrac { 2 } { \sqrt { 5 } } \right) \\[4pt] & = \dfrac { x ^ \prime + 2 y ^ \prime } { \sqrt { 5 } } \end {align*} $$
اکنون عبارات $$ x $$ و $$ y$$ را در معادله قرار داده و آن را ساده میکنیم:
$$ \large \begin {align*} 8 { \left ( \dfrac { 2 x ^ \prime − y ^ \prime } { \sqrt { 5 } } \right ) } ^ 2 − 1 2 \left ( \dfrac { 2 x ^ \prime − y ^ \prime } { \sqrt { 5 } } \right ) \left ( \dfrac { x ^ \prime + 2 y ^ \prime }{ \sqrt { 5 } } \right ) + 1 7 { \left ( \dfrac { x ^ \prime + 2 y ^ \prime } { \sqrt { 5 } } \right ) } ^ 2 & = 2 0 \\[4pt] 8 \left ( \dfrac { ( 2 x ^ \prime − y ^ \prime )( 2 x ^ \prime − y ^ \prime ) } { 5 } \right )− 1 2 \left ( \dfrac { ( 2 x ^ \prime − y ^ \prime ) ( x ^ \prime + 2 y ^ \prime ) }{ 5 } \right ) + 1 7 \left ( \dfrac { ( x ^ \prime + 2 y ^ \prime )( x ^ \prime + 2 y ^ \prime ) } { 5 } \right ) & = 2 0 \\[4pt] 8 ( 4 { x ^ \prime } ^ 2 − 4 x ^ \prime y ^ \prime + { y ^ \prime } ^ 2 ) − 1 2 ( 2 { x ^ \prime } ^ 2 + 3 x ^ \prime y ^ \prime − 2 { y ^ \prime } ^ 2 ) + 1 7 ( { x ^ \prime } ^ 2 + 4 x ^ \prime y ^ \prime + 4 { y ^ \prime } ^ 2 ) & = 1 0 0 \\[4pt] 3 2 { x ^ \prime } ^ 2 − 3 2 x ^ \prime y ^ \prime + 8 { y ^ \prime } ^ 2 − 2 4 { x ^ \prime } ^ 2 − 3 6 x ^ \prime y ^ \prime + 2 4 { y ^ \prime } ^ 2 + 1 7 { x ^ \prime } ^ 2 + 6 8 x ^ \prime y ^ \prime + 6 8 { y ^ \prime } ^ 2 & = 1 0 0 \\[4pt] 25 { x ^ \prime } ^ 2 + 1 0 0 { y ^ \prime } ^ 2 & = 1 0 0 \\[4pt] \dfrac { 2 5 } { 1 0 0 } { x ^ \prime } ^ 2 + \dfrac { 1 0 0 } { 1 0 0 } { y ^ \prime } ^ 2 & = \dfrac { 1 0 0 } { 1 0 0 } \end {align*} $$
معادله در مختصات جدید برحسب $$ x'$$ و $$ y'$$ به صورت زیر است:
$$ \large \dfrac { { x ^ \prime } ^ 2 } { 4 } + \dfrac { { y ^ \prime } ^ 2 } { 1 } = 1 \nonumber $$
شکل ۸ نمودار این بیضی را نشان میدهد.
مثال ۴
نمودار معادله زیر را در دستگاه $$x'y'$$ رسم کنید:
$$ \large x ^ 2 + 1 2 x y − 4 y ^ 2 = 3 0 $$
حل: ابتدا $$ \cot(2\theta) $$ را به دست میآوریم:
$$ \large x ^ 2 + 1 2 x y − 4 y ^ 2 = 2 0 \rightarrow A = 1 , \; B = 1 2 , \; C = − 4 $$
$$ \large \begin {align*} \cot ( 2 \theta ) & = \dfrac { A − C } { B } \\ \cot ( 2 \theta ) & = \dfrac { 1 − ( − 4 ) } { 1 2 } \\ \cot ( 2 \theta ) & = \dfrac { 5 } { 1 2 } \end {align*} $$
از آنجایی که $$ \cot(2\theta)=\dfrac{5}{12} $$، میتوانیم مثلث مرجع شکل ۹ را رسم کنیم.

بنابراین، وتر به صورت زیر به دست میآید:
$$ \large \begin {align*} 5 ^ 2 + { 1 2 } ^ 2 & = h ^ 2 \\[4pt] 2 5 + 1 4 4 & = h ^ 2 \\[4pt] 1 6 9 & = h ^ 2 \\[4pt] h & = 1 3 \end {align*} $$
در ادامه، $$ \sin \theta $$ و $$ \cos \theta $$ را محاسبه میکنیم. برای این کار از اتحادهای نیمزاویه کمک میگیریم:
$$ \large \sin \theta = \sqrt { \dfrac { 1 − \cos ( 2 \theta ) }{ 2 } } = \sqrt { \dfrac { 1 − \dfrac { 5 } { 1 3 } }{ 2} } = \sqrt { \dfrac { \dfrac { 1 3 } { 1 3 } − \dfrac { 5 } { 1 3 } }{ 2 } } = \sqrt { \dfrac { 8 } { 1 3 } ⋅ \dfrac { 1 } { 2 } } = \dfrac { 2 }{ \sqrt { 1 3 } } $$
$$ \large \cos \theta = \sqrt { \dfrac { 1 + \cos ( 2 \theta ) }{ 2 } } = \sqrt { \dfrac { 1 + \dfrac { 5 } { 1 3 } } { 2 } } = \sqrt { \dfrac { \dfrac { 1 3 } { 1 3 } + \dfrac { 5 } { 1 3 } }{ 2} } = \sqrt { \dfrac { 1 8 } { 1 3 } ⋅ \dfrac { 1 } { 2 } } = \dfrac { 3 }{ \sqrt { 1 3 } } $$
حال $$ x $$ و $$ y $$ را به دست میآوریم:
$$ \large x = x ^ \prime \cos \theta − y ^ \prime \sin \theta $$
$$ \large x = x ^ \prime \left ( \dfrac { 3 } { \sqrt { 1 3 } } \right ) − y ^ \prime \left ( \dfrac { 2 } { \sqrt { 1 3 } } \right ) $$
$$ \large x = \dfrac { 3 x ^ \prime − 2 y ^ \prime } { \sqrt { 1 3 } } $$
و
$$ \large y = x ^ \prime \sin \theta + y ^ \prime \cos \theta $$
$$ \large y = x ^ \prime \left ( \dfrac { 2 }{ \sqrt { 1 3 } } \right ) + y ^ \prime \left ( \dfrac { 3 } { \sqrt { 1 3 } } \right) $$
$$ \large y = \dfrac { 2 x ^ \prime + 3 y ^ \prime } { \sqrt { 1 3 } } $$
اکنون $$ x=\dfrac{3x^\prime −2y^\prime }{\sqrt{13}} $$ و $$ y=\dfrac{2x^\prime +3y^\prime }{\sqrt{13}} $$ را در $$ x^2+12xy−4y^2=30 $$ قرار میدهیم:
$$ \large \begin {array} {rl} { \left ( \dfrac { 3 x ^ \prime − 2 y ^ \prime } { \sqrt {1 3 } } \right ) } ^ 2 + 1 2 \left ( \dfrac { 3 x ^ \prime − 2 y ^ \prime }{ \sqrt { 1 3 } } \right ) \left ( \dfrac { 2 x ^ \prime + 3 y ^ \prime } { \sqrt { 1 3 } } \right )− 4 { \left ( \dfrac { 2 x ^ \prime + 3 y ^ \prime }{ \sqrt { 1 3 } } \right ) } ^ 2 = 3 0 \\ \left ( \dfrac { 1 } { 1 3 } \right )[ { ( 3 x ^ \prime − 2 y ^ \prime ) } ^ 2 + 1 2 ( 3 x ^ \prime − 2 y ^ \prime ) ( 2 x ^ \prime + 3 y ^ \prime ) − 4 { ( 2 x ^ \prime + 3 y ^ \prime ) } ^ 2 ] = 3 0 \\ \left ( \dfrac { 1 }{ 1 3 } \right )[ 9 { x ^ \prime } ^ 2 − 1 2 x ^ \prime y ^ \prime + 4 { y ^ \prime } ^ 2 + 1 2 ( 6 { x ^ \prime } ^ 2 + 5 x ^ \prime y ^ \prime − 6 { y ^ \prime } ^ 2 ) − 4 ( 4 { x ^ \prime } ^ 2 + 1 2 x ^ \prime y ^ \prime + 9 { y ^ \prime } ^ 2 ) ] = 3 0 \\ \left ( \dfrac { 1 } { 1 3 } \right ) [ 9 { x ^ \prime } ^ 2 − 1 2 x ^ \prime y ^ \prime + 4 { y ^ \prime } ^ 2 + 7 2 { x ^ \prime } ^ 2 + 6 0 x ^ \prime y ^ \prime − 7 2 { y ^ \prime } ^ 2 − 1 6 { x ^ \prime } ^ 2 − 4 8 x ^ \prime y ^ \prime − 3 6 { y ^ \prime } ^ 2 ] = 3 0 \\ \left ( \dfrac { 1 } { 1 3 } \right ) [ 6 5 { x ^ \prime } ^ 2 − 1 0 4 { y ^ \prime } ^ 2 ] = 3 0 \\ 6 5 { x ^ \prime } ^ 2 − 1 0 4 { y ^\prime } ^ 2 = 3 9 0 \\ \dfrac { { x ^ \prime } ^ 2 } { 6 } − \dfrac { 4 { y ^ \prime } ^ 2 } { 1 5 } = 1 \end {array} $$
شکل ۱۰ نمودار هذلولی $$ \dfrac{{x^\prime }^2}{6}−\dfrac{4{y^\prime }^2}{15}=1 $$ را نشان میدهد.
تعیین مقاطع بدون دوران محورها
اکنون به نقطه اول باز میگردیم. چگونه میتوانیم نوع مقطع مخروطی را که معادله آن داده شده تعیین کنیم؟
وقتی محورها دوران یافتهاند چه اتفاقی میافتد؟ فرم عمومی مقطع مخروطی را در نظر بگیرید:
$$ \large A x ^ 2 + B x y +C y ^ 2 + D x + Ey + F = 0 $$
اگر فرمولهای دوران را به این معادله اعمال کنیم، خواهیم داشت:
$$ \large A′ { x ^ \prime } ^ 2 + B′ x ^ \prime y ^ \prime + C′{ y ^ \prime } ^ 2 + D′ x ^ \prime + E′ y ^ \prime + F′ = 0 $$
میتوان نشان داد که:
$$ \large B ^ 2 − 4 A C = { B′ } ^ 2 − 4 A′ C′ $$
این عبارت بعد از دوران تغییری نمیکند، به همین دلیل آن را عبارت تغییرناپذیر مینامیم. مبیّن $$ B^2−4AC $$ تغییرناپذیر است و بعد از دوران بدون تغییر باقی میماند. از آنجایی که مبیّن بدون تغییر میماند، با استفاده از آن میتوانیم نوع مقطع را مشخص کنیم.
استفاده از مبیّن برای تعیین مقطع
اگر معادله
$$ \large A x ^ 2 + B x y + C y ^ 2 + D x + E y + F = 0 \;\;\;\;\; (8)$$
در اثر دوران محورها به معادله
$$ \large A′ { x ^ \prime } ^ 2 + B′ x ^ \prime y ^ \prime + C′{ y ^ \prime } ^ 2 + D′ x ^ \prime + E′ y ^ \prime + F′ = 0 \;\;\;\;\; (9)$$
تبدیل شود، آنگاه، داریم:
$$ \large B ^ 2 − 4 A C = { B′ } ^ 2 − 4 A′ C′ $$
معادله $$ Ax^2+Bxy+Cy^2+Dx+Ey+F=0 $$ یک بیضی، یک سهمی، یک هذلولی یا یک مورد تباهیده است.
- اگر $$ B^2−4AC<0 $$، آنگاه مقطع مخروطی یک بیضی است.
- اگر $$ B^2−4AC=0 $$، آنگاه مقطع مخروطی یک سهمی است.
- اگر $$ B^2−4AC>0 $$، آنگاه مقطع مخروطی یک هذلولی است.
مثال ۵
مقاطع مخروطی مربوط به معادلات بدون دوران زیر را تعیین کنید.
- الف) $$ 5 x ^ 2 + 2 \sqrt { 3 } x y + 2 y^ 2 − 5 = 0 $$
- ب) $$ 5 x ^ 2 + 2 \sqrt { 3 } x y +1 2 y ^ 2 −5 = 0 $$
حل الف: ابتدا $$A$$، $$ B $$ و $$ C $$ را تعیین میکنیم:
$$ \large \underbrace { 5 } _ { A } x ^ 2 + \underbrace { 2 \sqrt { 3 } } _ { B } x y + \underbrace { 2 } _ { C } y ^ 2 − 5 = 0 $$
مبیّن به صورت زیر است:
$$ \large \begin {align*} B ^ 2 − 4 A C & = { ( 2 \sqrt { 3 } ) } ^ 2 − 4 ( 5 ) ( 2 ) \\ & = 4 ( 3 ) −4 0 \\ & = 1 2 − 4 0 \\ & = − 2 8 < 0 \end {align*} $$
بنابراین، $$ 5x^2+2\sqrt{3}xy+2y^2−5=0 $$ یک بیضی را نشان میدهد.
حل ب: ابتدا $$A$$، $$ B $$ و $$ C $$ را تعیین میکنیم:
$$ \large \underbrace { 5 } _ { A } x ^ 2 + \underbrace { 2 \sqrt { 3 } } _ { B } x y + \underbrace { 1 2 } _ { C } y ^ 2 − 5 = 0 \nonumber $$
مبیّن به صورت زیر به دست میآید:
$$ \large \begin {align*} B ^ 2 − 4 A C & = { ( 2 \sqrt { 3 } ) } ^ 2 − 4 ( 5 ) ( 1 2 ) \\ & = 4 ( 3 ) − 2 4 0 \\ & = 1 2 − 2 4 0 \\ & = − 2 2 8 < 0 \end {align*} $$
بنابراین، $$5x^2+2\sqrt{3}xy+12y^2−5=0$$ معادله یک بیضی است.
جمعبندی
معادلات اصلی که باید آنها را به خاطر داشته باشید به صورت زیر هستند.
- معادله عمومی یک مقطع مخروطی:
$$ \large A x ^ 2 + B x y + C y ^ 2 + D x + E y + F = 0 $$
- دوران یک مقطع مخروطی:
$$ \large x = x ^ \prime \cos \theta − y ^ \prime \sin \theta \\ \large y = x ^ \prime \sin \theta + y ^ \prime \cos \theta $$
- زاویه دوران:
$$ \large \theta , \; \; \; \cot ( 2 \theta ) = \dfrac { A − C } { B } $$
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
^^










