اتحاد چاق و لاغر چیست؟ – اثبات، فرمول، نمونه سئوال – به زبان ساده

در آموزش‌های قبلی مجله فرادرس، با اتحادها و یکی از انواع مهم آن‌ها، یعنی اتحاد مکعب آشنا شدیم. در این آموزش‌ از مجله فرادرس می‌خواهیم با اتحاد مجموع و تفاضل دو مکعب آشنا شویم که به اتحاد چاق و لاغر و اتحاد فیل و فنجان نیز معروف است.

اتحاد چاق و لاغر چیست؟

همان‌طور که گفتیم، اتحاد چاق و لاغر به اتحاد مجموع یا تفاضل مکعب دو جمله گفته می‌شود. اتحاد چاق و لاغر را می‌توان برای دو حالت زیر بیان کرد:

• چندجمله‌ای $$a^3+b^3$$ که مجموع دو مکعب نامیده می‌شود و به عبارت ساده‌تر، مجموع توان سوم دو متغیر است.
• چندجمله‌ای $$a^3-b^3$$ که تفاضل دو مکعب نامیده می‌شود و به عبارت ساده‌تر، تفاضل توان سوم دو متغیر است.

اتحاد چاق و لاغر یک تساوی است که مجموع یا تفاضل دو مکعب را تجزیه می‌کند. در ادامه، این تساوی‌ها را معرفی می‌کنیم.

اتحاد چاق و لاغر مجموع مکعبات به صورت زیر است (برای به خاطر سپردن این اتحاد، به علامت‌ها دقت کنید):

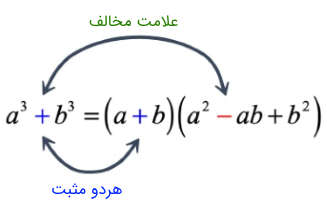
اتحاد چاق و لاغر تفاضل مکعبات نیز به شکل زیر بیان می‌شود (برای به خاطر سپردن این اتحاد، به علامت‌ها دقت کنید):

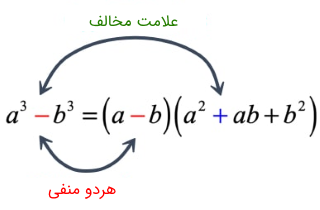
چرا چاق و لاغر؟

احتمالاً این پرسش برایتان پیش آمده که چرا به این اتحاد چاق و لاغر می‌گویند. فقط به دلیل ظاهر این اتحاد است که این نام را بر این اتحاد نهاده‌اند! در واقع یکی از دو پرانتز بزرگ‌ (چاق) و دیگری کوچک (لاغر) است. شکل‌های زیر این موضوع را به خوبی نشان می‌دهند.

اتحاد را برای مجموع مکعبات می‌نویسیم:

برای تفاضل مکعبات نیز داریم:

اگر به تصاویر بالا و اندازه عبارات داخل پرانتزها دقت کنید، دلیل این نام‌گذاری را خواهد فهمید.

اثبات اتحاد چاق و لاغر

اثبات اتحاد چاق و لاغر را می‌توان برای دو حالت مجموع و تفاضل بیان کرد.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی در فرادرس

کلیک کنید

اثبات اتحاد چاق و لاغر مجموع

باید تساوی زیر را اثبات کنیم:

$$\large (a+b)(a^{2}–ab+b^{2})=a^{3}+b^{3}$$

با استفاده از خاصیت‌ توزیع‌پذیری یا پخش‌پذیری، سمت چپ عبارت بالا را می‌توانیم به صورت زیر بنویسیم:

$$\large \left ( a \right ) \left ( a ^ { 2 } –a b + b ^ { 2 } \right ) + \left ( b \right ) \left ( a ^ { 2 } – a b + b ^ { 2 } \right )$$

اکنون $$a$$ را در پرانتز اول ضرب می‌کنیم:

$$\large \left ( a ^ { 3 } –a ^ { 2 } b + a b^ { 2 } \right ) + \left ( b \right ) \left ( a ^ { 2 } - a b + b ^ { 2 } \right )$$

سپس $$b$$ را در پرانتز دوم ضرب می‌کنیم:

$$\large \left ( a ^ { 3 } – a ^ { 2 } b + a b ^ { 2 } \right ) + \left ( a ^ { 2 } b – a b ^ { 2 } + b ^ { 3 } \right )$$

با چیدن جمله‌های مشابه در کنار یکدیگر، خواهیم داشت:

$$\large a ^ { 3 } - a ^ { 2 } b + a^ { 2 } b+ a b ^ { 2 } - a b ^ { 2 } + b ^ { 3 }$$

در نهایت، با حذف جملات قرینه، به عبارت زیر می‌رسیم:

$$\large a ^ 3 + b ^ 3$$

و اثبات کامل می‌شود.

اثبات اتحاد چاق و لاغر تفاضل

باید تساوی زیر را اثبات کنیم:

$$\large (a-b)(a^{2}+ab+b^{2})=a^{3}-b^{3}$$

با استفاده از خاصیت‌ توزیع‌پذیری یا پخش‌پذیری، سمت چپ عبارت بالا را می‌توانیم به صورت زیر بنویسیم:

$$\large \left ( a \right ) \left ( a ^ { 2 } + a b + b ^ { 2 } \right ) - \left ( b \right ) \left ( a ^ { 2 } + a b + b ^ { 2 } \right )$$

اکنون $$a$$ را در پرانتز اول ضرب می‌کنیم:

$$\large \left ( a ^ { 3 } +a ^ { 2 } b + a b^ { 2 } \right ) - \left ( b \right ) \left ( a ^ { 2 } + a b + b ^ { 2 } \right )$$

سپس $$b$$ را در پرانتز دوم ضرب می‌کنیم:

$$\large \left ( a ^ { 3 } + a ^ { 2 } b + a b ^ { 2 } \right ) - \left ( b a ^ { 2 } + a b ^ { 2 } + b ^ { 3 } \right )$$

با چیدن جمله‌های مشابه در کنار یکدیگر، خواهیم داشت:

$$\large a ^ { 3 } + a b ^ { 2 } + b a^ { 2 } - b a ^ { 2 } - a b ^ { 2 } - b ^ { 3 }$$

در نهایت، با حذف جملات قرینه، به عبارت زیر می‌رسیم:

$$\large a ^ 3 - b ^ 3$$

و می‌بینیم که اثبات کامل می‌شود.

تعبیر هندسی اتحاد چاق و لاغر

در این بخش می‌خواهیم تعبیر هندسی دو حالت اتحاد چاق و لاغر، یعنی تفاضل مکعب و مجموع مکعب، را شرح دهیم.

تعبیر هندسی تفاضل دو مکعب

دو توان سوم $$x$$ و $$y$$، یعنی $$x^3$$ و $$y ^ 3$$ را با مکعب‌های زیر نشان می‌دهیم.

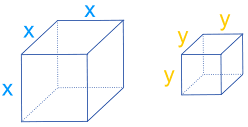
مکعب بزرگ‌تر را می‌توان به چهار مکعب کوچک‌تر با نام‌های C ،B ،A و D تقسیم کرد که هر ضلع مکعب A برابر با $$y$$ است. شکل زیر این موضوع را به خوبی نشان می‌دهد.

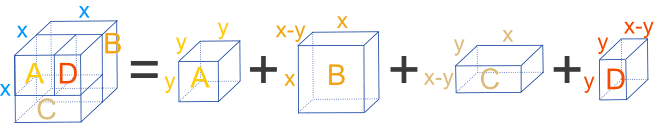
حجم مکعب‌ها به صورت زیر است:

• حجم مکعب A: $$y^3$$
• حجم مکعب B: $$x^2(x-y)$$
• حجم مکعب C: $$xy(x-y)$$
• حجم مکعب D: $$y^2(x-y)$$

مکعب‌های C ،B ،A و D مکعب بزرگ را به حجم $$x^3$$ تشکیل می‌دهند:

$$\large \begin {align*} x ^ 3 & = y ^ 3 + x ^ 2 ( x − y ) + x y ( x − y ) + y ^ 2 ( x − y ) \\ x ^ 3 − y ^ 3 & = x ^ 2 ( x − y ) + x y ( x − y ) + y ^ 2 ( x − y ) \\ x ^ 3 − y ^ 3 & = ( x − y ) ( x ^ 2 + x y + y ^ 2) \end {align*}$$

همان‌طور که می‌بینیم، تساوی آخر اتحاد چاق و لاغر را برای تفاضل مکعبات نشان می‌دهد.

تعبیر هندسی مجموع دو مکعب

اما تعبیر هندسی اتحاد چاق و لاغر برای مجموع مکعبات چگونه است؟ از نظر هندسی، برای محاسبه مجموع $$a^3+b^3$$ می‌توانیم دو مکعب به اضلاع $$a$$ و $$b$$ را در نظر بگیریم. شکل زیر این موضوع را به خوبی نشان می‌دهد (فرض کرده‌ایم $$a$$ بزرگ‌تر از $$b$$ است).

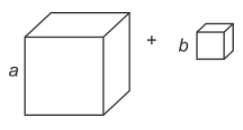
مکعب کوچک‌تر را می‌توان مطابق شکل زیر روی مکعب بزرگ‌تر قرار داد.

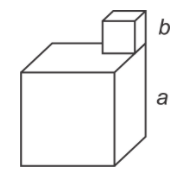
مطابق شکل زیر، خطوط فرضی را رسم می‌کنیم و به یک مکعب بزرگ‌تر مانند شکل زیر می‌رسیم.

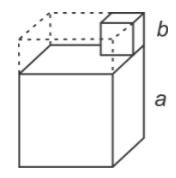
حجم کل مکعب مستطیل حاصل (همراه با مکعب مستطیل فرضی) به صورت زیر به دست می‌آید:

$$\large V = a \times a \times ( a + b ) = a ^ 2 ( a + b )$$

بخش فرضی مکعب مستطیل بالا را می‌توانیم مطابق شکل زیر به دو قسمت ۱ و ۲ تقسیم کنیم.

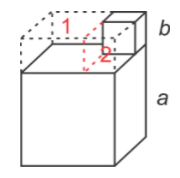
مجموع حجم دو مکعب واقعی، برابر با تفاضل حجم کل مکعب مستطیل (همراه با بخش فرضی) و حجم بخش فرضی (۱ و ۲) است:

$$\large V_{a,b}= a ^ { 2 } ( a + b ) - [\underbrace { a b ( a - b )} _{\text {} 1}+\underbrace { b^ { 2 } (a - b ) } _ { \text {} 2 } ]$$

اگر از جمله مشترک $$b(a-b)$$ درون براکت فاکتور بگیریم، عبارت بالا را می‌توانیم به صورت زیر بنویسیم:

$$\large V_{a,b} = a ^ 2 ( a + b ) - b ( a - b ) [a + b ]$$

توجه کنید که هر دو جمله یک عامل مشترک $$( a + b )$$ دارند. با فاکتور گرفتن از این عامل مشترک، می‌توان نوشت:

$$\large V_{a,b} = ( a + b ) ( a ^ 2 - ab+b^2)$$

عبارت درون پرانتز دوم را ساده می‌کنیم و به عبارت زیر می‌رسیم:

$$\large V_{a,b} = (a+b) ( a ^ 2 - ab + b ^ 2 )$$

آنچه به دست آورده‌ایم، مجموع حجم دو مکعب موجود، یعنی $$a^3 + b ^ 3$$ است. این یعنی تساوی زیر را داریم که همان اتحاد چاق و لاغر است:

$$\large a ^ 3 + b ^ 3 = ( a + b ) (a ^ 2 - a b + b ^ 2 )$$

مثال های اتحاد چاق و لاغر

در این بخش، چند نمونه سوال اتحاد چاق و لاغر را بررسی می‌کنیم.

مثال اول اتحاد چاق و لاغر

عبارت $$x ^ 3 + 125$$ را تجزیه کنید.

حل: با توجه به تساوی $$125 = 5 ^ 3$$، این عبارت را می‌توانیم با استفاده از اتحاد چاق و لاغر به صورت زیر تجزیه کنیم:

$$\large \begin {aligned} x ^ { 3 } + 1 2 5 & = ( x ) ^ { 3 } + (5 ) ^ { 3 } \\ & = ( x + 5 ) \left [ x ^ { 2 } - ( x ) ( 5 ) + 5 ^ { 2 } \right ] \\ & = ( x + 5 ) \left ( x ^ { 2 } - 5 x + 2 5 \right ) \end {aligned}$$

مثال دوم اتحاد چاق و لاغر

عبارت $$16m^{3}+54n^{3}$$ را تجزیه کنید.

حل: ابتدا از $$2$$ فاکتور می‌گیریم:

$$\large 2 \left ( 8 m ^ { 3 } + 2 7 n ^ { 3 } \right )$$

با توجه به تساوی‌های $$8m^3= (2m)^3$$ و $$27n^3=(3n)^3$$، عبارت بالا را می‌توانیم به صورت زیر بنویسیم:

$$\large 2 [( 2 m )^ { 3 } + (9 n ^ { 3 } ) ]$$

با در نظر گرفتن دو جمله $$a=2m$$ و $$b=3n$$ و استفاده از اتحاد چاق و لاغر، خواهیم داشت:

$$\large 2 \left [ (2 m )^2 + ( 3 n )^2 \right ] = 2 \left ( 2 m + 3 n \right ) \left [ \left ( 2 m \right ) ^{ 2 } - \left ( 2 m \right ) \left ( 3 n \right ) + \left ( 3 n \right ) ^ { 2 } \right ]$$

بنابراین، خواهیم داشت:

$$\large 2 \left ( 2 m + 3 n \right ) \left [ 4 m ^ { 2} - \left ( 2 m \right ) \left ( 3 n \right ) + 9n ^ { 2 } \right ]$$

و در نهایت، عبارت مورد نظر به صورت زیر تجزیه خواهد شد:

$$\large 2 \left ( 2 m + 3 n \right ) \left ( 4 m^ { 2 } - 6 m n + 9 n ^ { 2 } \right )$$

مثال سوم اتحاد چاق و لاغر

عبارت $$r^{9}-8s^{6}$$ را تجزیه کنید.

حل: این عبارت را می‌توانیم به صورت زیر بنویسیم:

$$\large \left ( r ^ { 3 } \right ) ^ { 3 } - \left ( 2 s ^ { 2 } \right ) ^ { 3 }$$

با در نظر گرفتن $$a=r^{3}$$ و $$b=2s^{2}$$، می‌بینیم که عبارت بالا به صورت $$a ^ 3 - b ^ 3$$ است. بنابراین، می‌توانیم از اتحاد چاق و لاغر زیر استفاده کنیم:

$$\large a ^ 3 - b ^ 3 = \left(a-b\right)\left(a^{2}+ab+b^{2}\right)$$

با جایگزینی $$a=r^{3}$$ و $$b=2s^{2}$$، خواهیم داشت:

$$\large \left ( r ^ { 3 } - 2 s ^ { 2 } \right ) \left [ \left ( r ^ { 3 } \right ) ^ { 2 } + \left ( r ^ { 3 } \right ) \left ( 2 s ^ { 2 } \right ) + \left ( 2 s ^ { 2 } \right ) ^ { 2 } \right ]$$

در نهایت، تجزیه عبارت به صورت زیر خواهد بود:

$$\large \left ( r ^ { 3 } - 2 s ^ { 2 } \right ) \left ( r ^ { 6 } + 2 r ^ { 3 } s ^ { 2 } + 4 s ^ { 4 } \right )$$

مثال چهارم اتحاد چاق و لاغر

عبارت $$1 - 216 { x ^ 3 } { y ^ 3 }$$ را تجزیه کنید.

حل: این مثال شاید در نگاه نخست دشور به نظر برسد. اما با کمی دقت و استفاده از آنچه درباره اتحاد چاق و لاغر گفتیم، می‌توانید آن را حل کنید. اگر کمی دقت کنیم، مشاهده می‌کنیم که می‌توان دو تساوی $$1 = (1)(1)(1) = 1 ^ 3$$ و $$216 = (6)(6)(6) = 6 ^ 3$$ را نوشت و به سادگی، عبارت را به صورت زیر تجزیه کرد:

$$\large \begin {aligned} 1 - 216 x ^ { 3 } y ^ { 3 } & = ( 1 ) ^ { 3 } - ( 6 x y ) ^ { 3 } \\ & = ( 1 - 6 x y ) \left [ ( 1 ) ^ { 2 } + ( 1 ) ( 6 x y ) + ( 6 x y ) ^ { 2 } \right ] \\ & = ( 1 - 6 x y ) \left ( 1 + 6 x y + 3 6 x ^ { 2 } y ^ { 2 } \right ) \end {aligned}$$

مثال پنجم اتحاد چاق و لاغر

عبارت $$x ^ 6 - y ^ 6$$ را تجزیه کنید.

حل: این عبارت را می‌توان به دو صورت زیر نوشت:

$$\large \begin{align*} x ^ 6 - y ^ 6 & = (x^2)^ 3 - (y^2)^3 \\ x ^ 6 - y ^ 6 &= (x ^ 3 )^ 2 - (y ^ 3 ) ^ 2 \end {align*}$$

با هر دو تساوی می‌توان مسئله را حل کرد. ابتدا فرض کنید اولی، یعنی تفاضل مکعب دو جمله $$x^2$$ و $$y ^ 2$$ را در نظر می‌گیرم. بنابراین، خواهیم داشت:

$$\large \begin {aligned} x ^ { 6 } - y ^ { 6 } & = \left ( x ^ { 2 } \right ) ^ { 3 } - \left ( y ^ { 2 } \right ) ^ { 3 } \\ & = \left ( x ^ 2 - y ^ 2 \right ) \left ((x ^ 2 )^ 2 + (x^2 ) (y ^ 2 ) + ( y ^ 2 ) ^ 2 \right ) \\ & = (x-y)(x+y) (x ^ 4 + x^2 y ^2+ y ^ 4 ) \\ & = ( x - y ) ( x + y) (x^ 4 + 2 x ^ 2 y ^ 2 - x ^ 2 y ^ 2 + y ^ 4 )\\ & = ( x - y ) ( x + y) [ ( x ^ 4 + 2 x ^2 y ^ 2 + y ^ 4 )- x ^ 2 y ^ 2 ] \\ & = ( x - y ) ( x + y) [ ( x ^2+ y ^ 2 ) ^ 2- x ^ 2 y ^ 2 ] \\ & = ( x - y ) ( x + y) [(x ^ 2 + y ^ 2 - xy )(x ^ 2 + y ^ 2 + xy)] \\ & = ( x - y ) ( x + y) (x ^ 2 - xy + y ^ 2)(x ^ 2 + xy + y ^ 2) \end {aligned}$$

روش دیگر، در نظر گرفتن اتحاد مزدوج برای دو جمله $$x^3$$ و $$y^ 3$$ و سپس استفاده از اتحاد چاق و لاغر است:

$$\large \begin {aligned} x ^ { 6 } - y ^ { 6 } & = \left ( x ^ { 3 } \right ) ^ { 2 } - \left ( y ^ { 3 } \right ) ^ { 2 } \\ & = \left ( x ^ { 3 } + y ^ { 3 } \right ) \left ( x ^ { 3 } - y ^ { 3 } \right ) \\ & = \left [ ( x + y ) \left ( x ^ { 2 } - x y + y ^ { 2 } \right ) \right ] \left [ ( x - y ) \left ( x ^ { 2 } + x y + y ^ { 2 } \right ) \right ] \\ & = ( x + y ) \left ( x ^ { 2 } - x y + y ^ { 2 } \right ) ( x - y ) \left ( x ^ { 2 } + x y + y ^ { 2 } \right ) \end {aligned}$$