آموزش حسابان یازدهم – از صفر تا صد + حل مثال و تمرین

حسابان یازدهم که با عنوان حسابان یک نیز شناخته می‌شود، یکی از دروس تخصصی دانش‌آموزان رشته ریاضی و فیزیک در مقطع متوسطه دوم محسوب می‌شود. در این درس ریاضی مهم مباحثی مانند جبر و معادله، مفهوم تابع، شناخت انواع توابع از جمله توابع نمایی و لگاریتمی، مثلثات و در نهایت حد و پیوستگی کاملا توضیح داده می‌شود. این مطلب از مجله فرادرس به آموزش حسابان یازدهم همراه با حل مثال و تمرین اختصاص دارد.

آموزش حسابان یازدهم شامل چه مباحثی است؟

کتاب حسابان ۱ شامل پنج فصل است که هر یک مقدمه‌ای برای فصل بعد است. به همین دلیل مهم است که قدم به قدم همراه با فصل‌های کتاب پیش بروید. برای مثال، اگر بخواهید مسائل حدگیری در فصل آخر را به راحتی حل کنید، لازم است ابتدا به انواع تابع و ویژگی‌های هر کدام در فصل‌های قبل کاملا مسلط شوید. آموزش حسابان یازدهم در مباحث زیر خلاصه می‌شود:

1. فصل اول - جبر و معادله: آشنایی با دنباله‌های حسابی و هندسی، معادلات درجه دوم، معادلات گویا و گنگ، مفهوم قدر مطلق و آشنایی با هندسه تحلیلی
2. فصل دوم - تابع: شناخت تابع و ویژگی‌های آن، انواع تابع، وارون تابع و اعمال مختلف روی آن
3. فصل سوم - توابع نمایی و لگارتیمی: لگاریتم و ویژگی‌های آن، حل معادلات لگاریتمی
4. فصل چهارم - مثلثات: مفهوم رادیان، نسبت‌های مثلثاتی، توابع و روابط مثلثاتی
5. فصل پنجم - حد و پیوستگی: مفهوم حد، حد چپ و راست، قضایای حد، رفع ابهام‌ها و پیوستگی

جبر و معادله

اولین بخش از آموزش حسابان یازدهم اختصاص دارد به توضیح دنباله‌ها، معادلات درجه دوم، معادلات گویا و گنگ، آشنایی با قدر مطلق و هندسه تحلیلی. در ادامه هر مبحث را در بخش مجزا توضیح می‌دهیم و در انتها حل مثال و تمرین خواهیم داشت.

مجموع جملات دنباله‌ های حسابی و هندسی

جدول زیر نشان می‌دهد تفاوت‌‌‌ مجموع جملات در دنباله‌ حسابی و هندسی طبق آموزش حسابان یازدهم چیست:

می‌دانیم دنباله حسابی به دنباله‌ای گفته می‌شود که در آن اختلاف بین هر دو جمله برابر است با یک عدد ثابت، در حالی که دنباله هندسی دنباله‌ای است که در آن نسبت هر دو جمله برابر است با یک عدد ثابت.

دنباله چیست؟

برای اینکه در ابتدای آموزش حسابان یازدهم با نحوه به دست آوردن مجموع جملات دنباله‌‌های حسابی و هندسی آشنا شویم، ابتدا بهتر است ببینیم دنباله چیست و دنباله‌های حسابی و هندسی چه تفاوت‌هایی با هم دارند. دنباله یا Sequence به یک مجموعه عدد گفته می‌شود که با نظم خاصی در کنار هم قرار گرفته‌اند و اگر به ارتباط هر عدد با عدد قبل و بعد از آن بیشتر دقت‌ کنید، ملاحظه می‌کنید که الگوی یکسانی بین تمام این اعداد برقرار است.

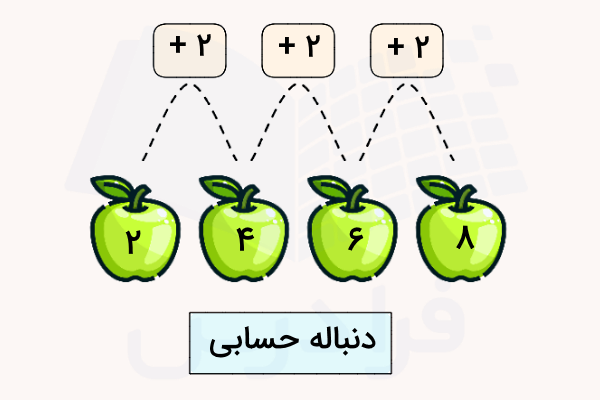
مهم‌ترین ویژگی‌های یک دنباله را می‌توانیم به شکل زیر در نظر بگیریم:

• هر کدام از اعداد یک دنباله، یک جمله یا Term نامیده می‌شود.
• دنباله‌ها می‌توانند متناهی یا نامتناهی باشند.
• دنباله‌ها را می‌توان به روش‌های مختلفی مانند فرمول صریح، رابطه بازگشتی یا جدول مقادیر توصیف کرد.
• فرمول صریح یک روش مستقیم برای محاسبه هر جمله دنباله ارائه می‌دهد.
• رابطه بازگشتی هر جمله را بر حسب یک یا چند جمله قبلی بیان می‌کند.
• جدول مقادیر فقط جملات دنباله را فهرست می‌کند.
• انواع مختلف دنباله‌ها عبارت‌اند از دنباله‌های حسابی، دنباله‌های درجه دو، دنباله‌های هندسی، دنباله‌های مثلثی، دنباله اعداد مربعی و ...

در آموزش حسابان یازدهم فقط به دنباله‌های حسابی و هندسی می‌پردازیم که موضوع بخش‌های بعد است.

دنباله حسابی و فرمول مجموع جملات آن

دنباله حسابی یا Arithmetic Sequence اولین مبحثی است که در آموزش حسابان یازدهم توضیح داده می‌شود. در این دنباله هر جمله از جمع کردن جمله قبلی خودش با یک عدد ثابت به‌ دست می‌آید. برای مثال، یک دنباله حسابی را در نظر بگیرید که در آن اولین جمله برابر است با $$a$$ و دومین جمله از جمع کردن $$a$$ با عدد ثابتی مانند $$d$$ به دست می‌آید.

در سومین جمله، جمله قبل ینی $$a+d$$ مجددا با عدد ثابت $$d$$ جمع می‌شود که حاصل برابر می‌شود با $$a+d+d$$. اگر این روند را به همین صورت ادامه دهیم، $$n$$ امین جمله برابر خواهد شد با $$a + (n-1)d$$. بنابراین مجموع جملات در یک دنباله حسابی با جمله اول $$a_1$$ و اختلاف بین جملات برابر با $$d$$، توسط فرمول زیر به دست می‌آید:

$$S_ n = \frac{ n}{2} (a_1 + a_n)$$

که در آن جمله  $$n$$ ام یا $$a_n$$ برابر است با:

$$a_ n = a_1 + (n-1) d$$

دنباله هندسی و فرمول مجموع جملات آن

در دنباله هندسی یا Geometric Sequence هر جمله با ضرب کردن جمله قبلی در یک جمله مشخص حاصل می‌شود. برای نمونه، طبق تصویر زیر اولین جمله دنباله هندسی برابر است با $$a$$. دومین جمله از ضرب این مقدار در $$q$$ حاصل می‌شود و جمله سوم با ضرب کردن جمله قبلی یعنی جمله دوم یا $$aq$$ در $$q$$ به دست می‌آید و به همین ترتیب. بنابراین $$n$$ امین جمله این دنباله هندسی برابر می‌شود با $$aq^{n-1}$$:

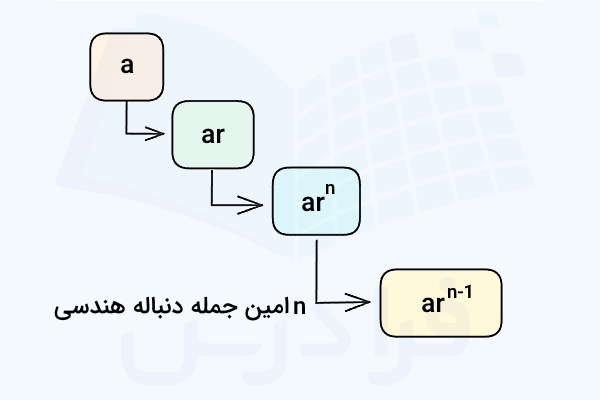
به این ترتیب اگر اولین جمله ما در یک دنباله هندسی $$a$$ و قدر نسبت بین جملات برابر با $$q$$ باشد، فرمول مجموع جملات به شکل زیر است:

$$S_ n = a \ \frac{1- q^n}{1-q}$$

معادلات درجه دوم

دومین بخش از فصل اول آموزش حسابان یازدهم اختصاص دارد به بررسی روابط بین ریشه‌های معادلات درجه دو و ضرایب این معادلات. می‌‌دانیم یک معادله درجه دو به شکل زیر است:

$$ax^2+ bx+ c = 0$$

دقت کنید شرط درجه دوم بودن یک معادله این است که $$a \neq 0$$. حل معادله درجه ۲ به معنای پیدا کردن پاسخ‌های آن یا مقادیر $$x$$ است که ریشه‌های معادله نامیده می‌شوند. مرسوم‌ترین روش حل معادله درجه دوم استفاده از روش دلتا است. ریشه‌های معادله درجه دو بالا طبق فرمول دلتا عبارت‌اند از:

$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$

علت اینکه می‌گوییم ریشه‌های معادله درجه دوم این است که به دلیل وجود علامت $$\pm$$ در فرمول بالا دو ریشه داریم. فرض کنید معادله‌ای به شکل زیر داریم:

$$x^2 - 7x +10 = 0$$

طبق فرمول دلتا ریشه‌های این معادله برابر‌اند با:

$$x = \frac{7 \pm \sqrt{49- 40}}{2} = \frac{7 \pm 3}{2} = \begin{cases}5 \\2\end{cases}$$

مجموع و حاصل‌ضرب این دو ریشه نیز عبارت‌اند از:

$$S = 2+5 = 7$$

$$P = 2 \times 5 =10$$

اما نکته جالب این است که می‌توانیم بدون حل معادله $$S$$ و $$P$$ را تعیین کنیم. در بخش‌های بعد به این موضوع خواهیم پرداخت.

فرمول مجموع ریشه ها

اگر ریشه اول و دوم یک معادله درجه دو را به ترتیب $$x_1$$ و $$x_2$$ بنامیم، مجموع این دو مقدار به شکل زیر خواهد شد:

$$S = x_1 + x_2 = \frac{-b }{2a} +\frac{ \sqrt{b^2 - 4ac}}{2a} + \frac{-b }{2a} -\frac{ \sqrt{b^2 - 4ac}}{2a} = \frac{-b }{a}$$

بنابراین برای معادله درجه دوم $$ax^2+ bx+ c = 0$$ مجموع ریشه‌ها همواره برابر است با $$S = \frac{-b }{a}$$.

فرمول حاصل‌ ضرب ریشه ها

اگر ریشه‌‌های اول و دوم یک معادله درجه دو را به ترتیب $$x_1$$ و $$x_2$$ بنامیم، حاصل‌ضرب این دو مقدار به شکل زیر خواهد شد:

$$P = x_1 x_2 = (\frac{-b }{2a} +\frac{ \sqrt{b^2 - 4ac}}{2a} )( \frac{-b }{2a} -\frac{ \sqrt{b^2 - 4ac}}{2a} )$$

رابطه بالا را می‌توانیم به نوعی یک اتحاد مزدوج در نظر بگیریم. بنابراین بدون اینکه دو پرانتز را در هم ضرب کنیم، حاصل آن ساده می‌شود:

$$P = x_1 x_2 = \frac{b^2 }{4a^2} -\frac{ b^2 - 4ac}{4a^2} =\frac{ c}{a}$$

بنابراین برای معادله درجه دوم $$ax^2+ bx+ c = 0$$ حاصل‌ضرب ریشه‌ها همواره برابر است با $$P =\frac{ c}{a}$$.

صفرهای تابع و روش هندسی حل معادلات

می‌‌دانیم هر تابع را می‌توان توسط یک رابطه (ضابطه) مانند $$f(x)$$ توصیف کرد. اگر این رابطه را برابر با صفر قرار دهیم، جواب‌های حاصل همان صفرهای معادله هستند:

$$f(x) = 0$$

در واقع اگر نمودار تابع را رسم کنیم، صفرهای تابع همان مولفه‌های x نقاطی هستند که از تلاقی نمودار تابع با محور xها حاصل می‌شوند. از این نکته می‌توانیم برای حل معادلات به روش هندسی استفاده کنیم. در این روش اگر معادله‌ای به شکل $$f(x) = g(x)$$ داشته باشیم که از برابری ضابطه دو تابع حاصل شده است، با رسم نمودار هر کدام از توابع $$f(x)$$ و $$g(x)$$ و سپس بررسی نقاط تلاقی این دو نمودار، می‌توانیم به جواب برسیم. کافی است مولفه افقی این نقاط تلاقی را به عنوان پاسخ در نظر بگیریم.

معادلات گویا و گنگ

منظور از معادلات گویا و گنگ معادلاتی است که به شکل کسری نوشته شده‌اند و شامل رادیکال نیز می‌شوند. حل این معادلات مستلزم ساده کردن جملات است که می‌توان به روش‌های مختلفی این فرآیند را انجام داد. تسلط به ساده‌سازی کسرها، انواع اتحادها، کوچکترین مضرب مشترک، نحوه به توان رساندن عبارت‌های رادیکالی، ساده کردن رادیکال‌ها و مفهوم دامنه و برد توابع گویا و چندجمله‌ای است. نکته مهم در حل معادلات گنگ و گویا این است که دقت کنیم پاسخ‌های به‌ دست آمده موجب صفر شدن مخرج کسرها یا منفی شدن عبارت‌های جبری زیر رادیکال نشوند.

قدر مطلق و ویژگی های آن

آخرین بخش از فصل اول آموزش حسابان اختصاص دارد به مفهوم قدر مطلق. می‌دانیم قدر مطلق هر عدد حقیقی $$a$$ به شکل زیر تعریف می‌شود:

$$|a| = \begin{cases} a & a \geq 0\\ -a & a < 0\end{cases}$$

اگر به جای عدد مشخص $$a$$ متغیر $$x$$ داخل قدر مطلق قرار بگیرد، تابع قدر مطلق را به شکل $$y = |x|$$ یا $$f (x) = |x|$$ خواهیم داشت که با توجه به تعریف بالا نمودار آن به شکل زیر رسم خواهد شد:

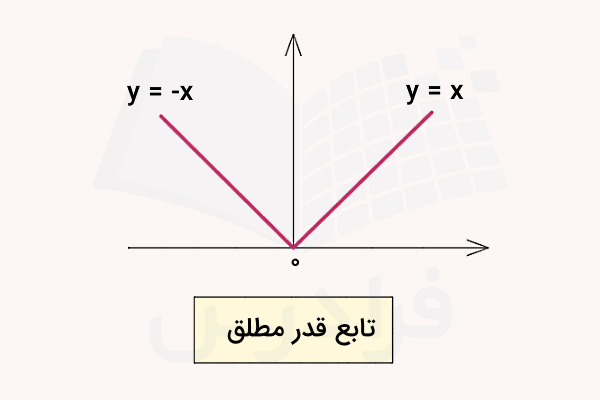
برخی از مهم‌ترین ویژگی‌های قدر مطلق را در ادامه فهرست کرده‌ایم:

• $$|x| = a \Rightarrow \begin{cases} x =a & x \geq a \\ x= -a & x < a \end{cases}$$
• $$|x|$$ همواره بزرگتر یا مساوی صفر است.
• $$|x| = |-x |$$
• $$\sqrt{x^2} = |x|$$
• $$|x|^2 = x^2$$

به این ترتیب اگر معادله‌ای به شکل $$|f(x)| = |g(x) |$$ داشته باشیم، جواب‌های این معادله معادل می‌شوند با جواب‌های دو معادله $$f(x) = g(x)$$ و $$f(x) = - g(x)$$. چنین معادلاتی را معادلات قدر مطلقی می‌نامیم.

آشنایی با هندسه تحلیلی

این بخش از آموزش حسابان یازدهم مقدمه‌ای است برای یادگیری بهتر درس هندسه ۳ که در پایه دوازدهم تدریس می‌شود. می‌دانیم موقعیت دقیق هر نقطه در صفحه را با مختصات آن نقطه می‌توان نمایش داد. حال اگر دو نقطه $$A = \left(\begin{array}{c}x_1\\ y_1\end{array}\right)$$ و $$B = \left(\begin{array}{c}x_2\\ y_2\end{array}\right)$$ را با مختصات مشخص داشته باشیم، طول پاره‌خط $$AB$$ یا فاصله بین این دو نقطه به شکل زیر محاسبه می‌شود:

$$AB =\sqrt {(x_2 -x_1)^2 + (y_2 -y_1)^2}$$

همچنین در این بخش تعاریف زیر مهم است:

• عمود منصف یک پاره‌خط به تمام نقاطی گفته می‌شود که فاصله آن‌ها از دو سر پاره‌خط به یک اندازه است.
• اگر دو خط عمود بر هم با شیب‌های $$m_1$$ , $$m_1$$ داشته باشیم، تساوی $$m_1m_2 = -1$$ همیشه برقرار است.
• اگر نقطه $$M$$ در وسط پاره‌خط $$AB$$ قرار گرفته باشد، مختصات آن برابر است با $$x_M = \frac{x_A + x_B}{2}$$ و $$y_M = \frac{y_A + y_B}{2}$$.
• فاصله عمودی نقطه $$A = \left(\begin{array}{c}x_0\\ y_0\end{array}\right)$$ از خطی با معادله $$ax + by + c = 0$$ توسط فرمول $$\frac {|ax_0 + by_0 + c |}{\sqrt{a^2 + b^2}}$$ محاسبه می‌شود.

حل مثال و تمرین از جبر و معادله

در این بخش چند نمونه مثال و تمرین از موضوعات این بخش خواهیم داشت تا آموزش حسابان یازدهم در این بخش تکمیل شود.

مثال ۱

هزینه یک تاکسی زمانی که مسافت اولیه‌ای به اندازه یک کیلومتر را می‌پیماید، برابر است با دو دلار. اگر به ازای هر یک کیلومتر بعدی به این مبلغ یک و نیم دلار اضافه شود، برای پیمودن بیست کیلومتر چه مبلغی نیاز است؟

پاسخ

ابتدا باید تشخیص دهیم دنباله ما هندسی است یا حسابی. چون در صورت سوال از عبارت «اضافه شود» استفاده شده است، پس نتیجه می‌گیریم جمله اول ما با یک و نیم دلار جمع می‌شود و به همین ترتیب. بنابراین یک دنباله حسابی داریم و برای پیدا کردن مبلغ معادل برای پیمودن بیست کیلومتر کافی است جمله بیستم در این دنباله را پیدا کنیم. با توجه به اینکه جمله اول $$2$$ و اختلاف مشترک $$1.5$$ است، جمله بیستم به شکل زیر محاسبه می‌شود:

$$a_ n = a_1 + (n-1) d$$

$$a_ {20} = 2 + (20-1) \times 1.5 = 30.5$$

مثال ۲

اگر $$\alpha$$ و $$\beta$$ ریشه‌های معادله $$x^2 + 4x + 6 = 0$$ باشند، معادله‌ای را پیدا کنید که ریشه‌‌های آن عبارت‌اند از $$\frac{1}{\alpha}$$ و $$\frac{1}{\beta}$$:

پاسخ

طبق فرمول‌های مجموع و حاصل‌ضرب ریشه‌ها، برای معادله داده شده خواهیم داشت:

$$S = \alpha + \beta= \frac{-b }{a}$$

$$$ P = \alpha \beta = \frac{ c}{a} $$

$$S = \frac{-4 }{1} = -4$$

$$P =\frac{ 6}{1} = 6$$

حالا مجموع دو ریشه موردنظر یعنی $$\frac{1}{\alpha}$$ و $$\frac{1}{\beta}$$ را محاسبه می‌کنیم:

$$S = \frac{1}{\alpha} + \frac{1}{\beta} = \frac{\alpha +\beta}{\alpha \beta}$$

ملاحظه می‌کنید که صورت و مخرج رابطه بالا معادل شد با مقادیری که به دست آوردیم. پس داریم:

$$S = \frac{\alpha +\beta}{\alpha \beta} = \frac{S}{P} = \frac{-4}{6}= \frac{-2}{3}$$

به همین شکل برای حاصل‌ضرب $$\frac{1}{\alpha}$$ و $$\frac{1}{\beta}$$ خواهیم داشت:

$$P= \frac{1}{\alpha } \times \frac{1}{\beta} = \frac{1}{\alpha \beta} = \frac{1}{P} = \frac{1}{6}$$

می‌دانیم اگر $$\alpha$$ و $$\beta$$ دو عدد دلخواه باشند به شکلی که $$S = \alpha + \beta$$ و $$P = \alpha \beta$$، آنگاه $$\alpha$$ و $$\beta$$ جواب‌های معادله $$x^2 - Sx +P = 0$$ هستند. بنابراین می‌توانیم بنویسیم:

$$x^2 - (\frac{-2}{3})x + \frac{1}{6} = 0$$

$$x^2 + \frac{2}{3}x + \frac{1}{6} = 0$$

اگر تمام جملات این معادله را در کسر یک ششم ضرب کنیم، خواهیم داشت:

$$6x^2 + 4x + 1 = 0$$

پس معادله به دست آمد.

مثال ۳

معادله $$|x| = x^2 - 2x$$ را به روش هندسی یا رسم نمودار حل کنید:

پاسخ

در این معادله دو تابع به شکل $$f(x) = x^2 - 2x$$ و $$g(x) = |x|$$ داریم. در قدم اول نمودار هر تابع را در یک دستگاه مختصات رسم می‌کنیم. تابع $$f$$ یک تابع درجه دو به شکل سهمی است و تابع $$g$$ یک تابع قدر مطلق است:

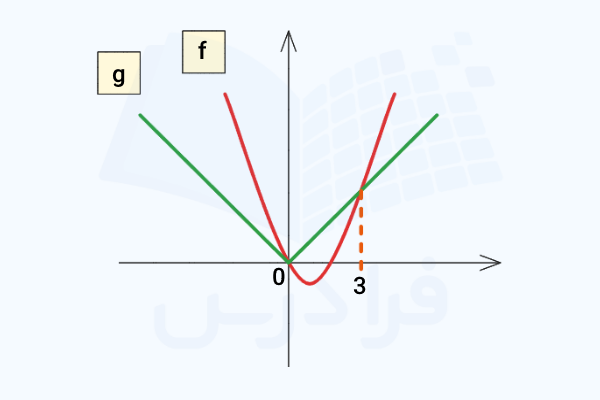
ملاحظه می‌کنید که این دو تابع در دو نقطه یکدیگر را قطع می‌کنند:

$$x = 0$$

$$x =3$$

این دو نقطه همان جواب‌های معادله $$|x| = x^2 - 2x$$ هستند.

مثال ۴

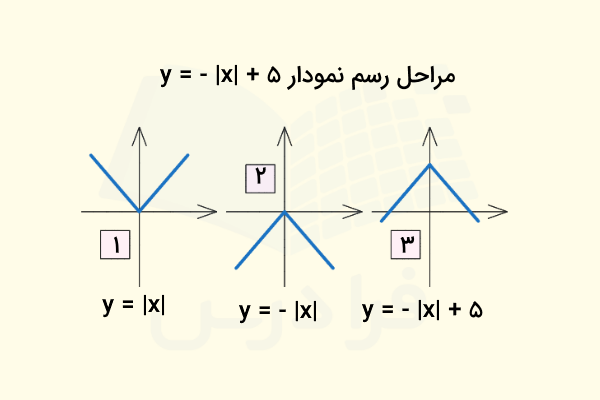
نمودار تابع $$y = - |x| + 5$$ را رسم کنید:

پاسخ

برای رسم چنین نموداری طبق مراحل زیر پیش می‌رویم:

1. ابتدا نمودار $$y = |x|$$ را رسم می‌کنیم.
2. آن را نسبت به محور x قرینه می‌کنیم.
3. نمودار نهایی را به اندازه پنج واحد در جهت مثبت محور y جابجا می‌کنیم.

حاصل به شکل زیر خواهد شد:

یادگیری حسابان با فرادرس

در این بخش چند فیلم آموزشی از مجموعه فرادرس به شما معرفی می‌شود که با هدف آموزش حسابان یازدهم و دوازدهم تهیه شده‌اند:

• فیلم آموزش حسابان ۱ – پایه یازدهم فرادرس
• فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین فرادرس
• فیلم آموزش حسابان ۲ – پایه دوازدهم فرادرس

تابع

در بخش بعدی از آموزش حسابان یازدهم با مفهوم تابع، انواع تابع، نحوه پیدا کردن وارون یا معکوس یک تابع و چگونگی انجام اعمال گوناگون روی یک تابع آشنا خواهید شد.

تعریف تابع چیست؟

در اولین قدم لازم است با تعریف دقیق تابع در ریاضی آشنا شویم. تابع یا Function به فرآیند، رابطه یا ضابطه‌ای گفته می‌شود که در آن هر عضو یا هر عنصر از یک مجموعه غیرصفر مانند $$A$$ به حداقل یک عضو از مجموعه غیرصفر دیگری مانند $$B$$ مرتبط می‌شود. این نوع رابطه که از اعضای یک مجموعه مثل $$A$$ (دامنه تابع) به اعضای مجموعه دیگری مانند $$B$$ (هم‌دامنه تابع) دیده می‌شود، همان تعریف تابع در ریاضی است که به شکل زیر نیز در زبان ریاضیات نمایش داده می‌شود:

$$f = \left\{ (a,b) | \ a \in A , b \in B\right\}$$

در این رابطه $$f$$ نماد تابع، $$\ a \in A$$ بیان کننده این است که عنصر $$a$$ عضوی از مجموعه $$A$$ و $$\ b \in B$$ نیز بیان کننده این است که عنصر $$b$$ عضوی از مجموعه $$B$$ است. به طور کلی در تشخیص تابع بودن یک ضابطه، لازم است به نکات زیر توجه کنیم:

• یک تابع زمانی مشخص می‌شود که دامنه، هم‌دامنه و دستور یا ضابطه‌ای که نحوه ارتباط بین اعضای دامنه و هم‌دامنه را نشان می‌دهد، مشخص باشند.
• هم‌دامنه مجموعه‌ای از اعداد یا اعضا است که خروجی تابع می‌تواند جزئی از آن باشد. به هم‌دامنه، دامنه مشترک نیز گفته می‌شود.
• تابع رابطه‌‌ای است که در آن هر عضو از مجموعه‌ای مانند $$A$$ فقط و فقط به یک عضو از مجموعه‌ای مانند $$B$$ مرتبط می‌‌شود.
• برد یک تابع زیرمجموعه‌ای از هم‌دامنه آن است.
• دو تابع $$f$$ و $$g$$ زمانی با هم برابر‌اند که دو شرط برقرار بماند، اول اینکه دامنه هر دو یکسان باشد و سپس به ازای هر $$x$$ از این دامنه، همواره داشته باشیم $$f(x) = g(x)$$.
• اگر دو تابع $$f$$ و $$g$$ به شکل $$f: A\rightarrow B$$ و $$g: B\rightarrow C$$ تعریف شوند، در این صورت ترکیب $$f$$ با $$g$$ به ازای هر $$x \in A$$ به شکل $$f(g(x))$$ یا $$fog$$ نشان داده می‌شود.

مساحت کره نمونه‌ای از یک مثال واقعی از تابع است. در فرمول مساحت کره که به شکل $$A = 4\pi r^2$$ نوشته می‌شود، همواره مساحت یا $$A$$ تابعی از شعاع کره یعنی $$r$$ است، چون با تغییر شعاع مساحت کره نیز تغییر می‌کند. به زبان ریاضیات می‌گوییم مساحت کره همواره تابعی از شعاع آن است. به همین ترتیب برای حجم کره و مساحت دایره نیز گفتن چنین عبارتی درست است. مثال دیگر از کاربرد تابع، قانون دوم نیوتن است. طبق این قانون، شتابی که جسم به دست می‌آورد، همواره تابعی از مجموع نیروهای وارد بر آن است.

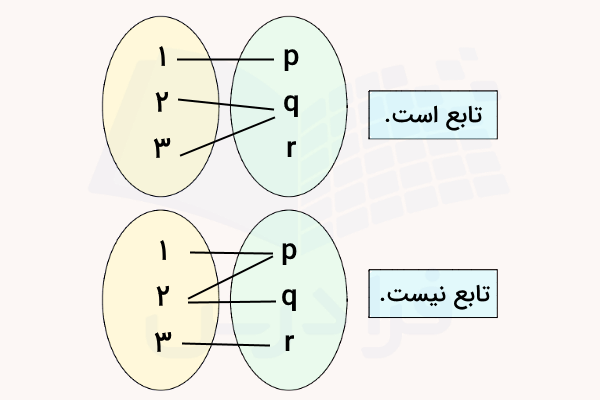
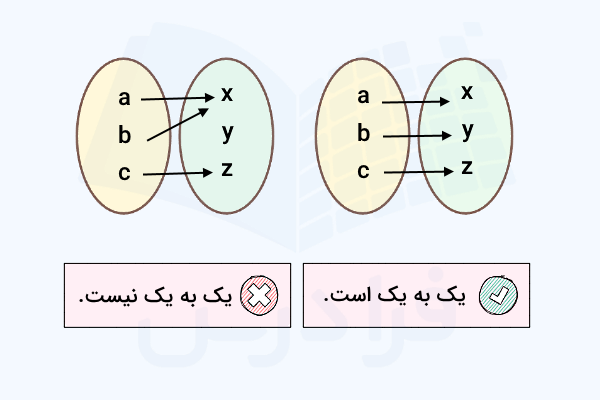
دو مجموعه بالای تصویر زیر یک تابع را نشان می‌دهند، در حالی که ارتباط بین اعضای دو مجموعه پایین‌تر نشان دهنده یک تابع نیست. با توجه به اینکه عدد $$2$$ به دو عضو از برد تابع مرتبط شده است، بنابراین نمی‌توانیم ارتباط این دو مجموعه را یک تابع در نظر بگیریم. این تابع را می‌توانیم به شکل نیز نشان دهیم که در آن مجموعه دامنه عبارت است از $$D = \left\{ 1,2,3\right\}$$ و برد نیز برابر است با $$R = \left\{ p,q\right\}$$:

$$f = \left\{ (1,p) , (2,q), (3,q) \right\}$$

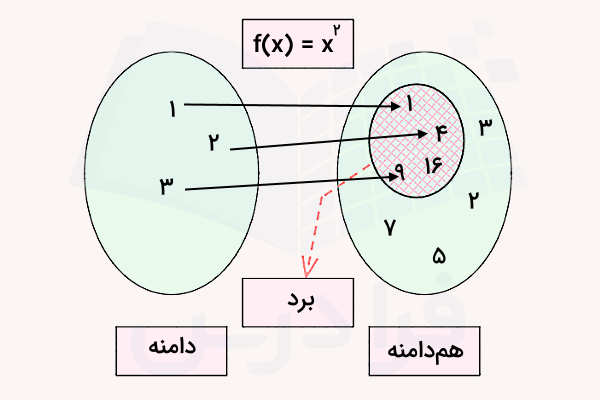
برای اینکه مفهوم هم‌دامنه را در مقایسه با برد بهتر متوجه شوید، به تصویر زیر دقت کنید. طبق این تصویر که نشان‌ دهنده تابعی با ضابطه $$x^2$$ است، برد شامل اعدادی مانند $$1, 4,9, 16$$ است که طبق ضابطه تابع با به توان دو رساندن اعضای دامنه حاصل می‌شوند، در حالی که هم‌دامنه شامل اعضای بیشتری است. در تصویر قبل نیز با اینکه مجموعه برد تابع دو عضو داشت، اما هم‌دامنه دارای سه عضو است.

رابطه یا فرمول ریاضیاتی توصیف کننده توابع می‌توانند با هم جمع شوند یا در هم ضرب شوند و .... برای دو تابع $$f$$ و $$g$$  روابط زیر را داریم:

• $$(f+g)(x) = f(x) + g(x)$$
• $$(f-g)(x) = f(x) - g(x)$$
• $$(f.g)(x) = f(x) .g(x)$$
• $$(kf(x))= k.f(x)$$ که در آن $$k$$ یک عدد حقیقی است.
• $$\frac{f}{g}(x) = \frac{f(x) }{g(x)}$$ که در آن $$g(x) \neq 0$$ است.

روش تشخیص تابع

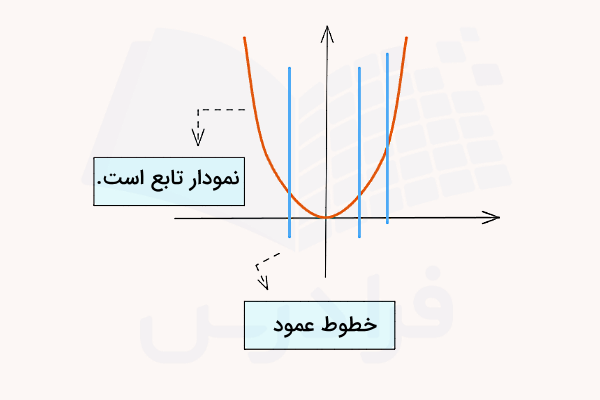
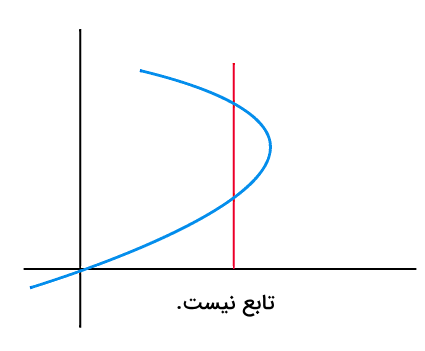
یکی از ساده‌ترین روش‌ها برای تشخیص تابع این است که ابتدا نمودار آن را رسم کنیم. سپس با رسم خطوط عمودی یا خطوطی موازی با محور y در نقاط مختلف، بینیم آیا این خطوط نمودار تابع را در بیش از یک نقطه قطع می‌کنند یا خیر. اگر فقط برای یکی از این خطوط بیش از دو نقطه تقاطع وجود داشت، این نمودار نشان دهنده یک تابع نیست.

دقت کنید برای رسم نمودار یک تابع کافی است ابتدا ضابطه یا رابطه آن تابع را پیدا کنیم. سپس با مقداردهی به جای $$x$$ و با در نظر گرفتن دامنه تابع، مقادیر $$f(x)$$ یا $$y$$ را به‌دست آوریم. برای مثال، در مورد تابع درجه دو نشان داده شده در تصویر قبل، ضابطه تابع معادل است با $$f(x) = y = x^2$$. نمودار این تابع به شکل یک سهمی است و همان‌طور که ملاحظه می‌کنید، یک تابع است:

این در حالی است که نمودار زیر نمودار یک تابع محسوب نمی‌شود:

انواع تابع

پس از اینکه تعریف و ویژگی‌های مهم یک تابع را در آموزش حسابان یازدهم آموختیم، در این بخش با انواع تابع، مشخصات و نمودار هر کدام به شکلی مختصر آشنا می‌شویم. با تابع یک به یک شروع می‌کنیم که در آن هر عضو متفاوت از دامنه فقط و فقط با یک عضو متمایز از برد متناظر است. تصویر زیر تمایز تابع یک به یک را با انواع دیگر توابع به درستی نشان می‌دهد:

روش آسان‌تر تشخیص یک به یک بودن تابع این است که نمودار آن را رسم کنیم. اگر خطوط موازی محور افقی این نمودار را در بیش از یک نقطه قطع کنند، تابع یک به یک نیست. در ادامه برخی از مهم‌ترین دسته‌بندی‌ها برای یک تابع را به طور خلاصه معرفی کرده‌ایم:

• تابع یک به یک: تابعی است که هر ورودی متفاوت خروجی متفاوتی نیز دارد.
• تابع پوشا: تابعی است که تمام مقادیر ممکن در برد را پوشش می‌دهد.
• تابع صعودی: تابعی است که با افزایش مقدار $$x$$ در آن مقدار $$f(x)$$ نیز افزایش می‌یابد.
• تابع نزولی: تابعی است که با افزایش مقدار $$x$$ در آن مقدار $$f(x)$$ کاهش می‌یابد.
• تابع زوج: تابعی است که به ازای هر $$x$$ در آن رابطه $$f(x) = f(-x)$$ همواره برقرار است.
• تابع فرد: تابعی است که به ازای هر $$x$$ در آن رابطه $$f(-x) = -f(x)$$ همواره برقرار است.
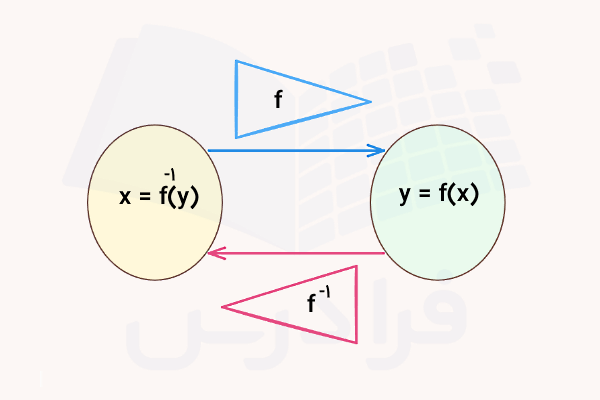
• تابع معکوس یا وارون: تابعی است که ورودی و خروجی تابع را جابجا می‌کند، به گونه‌ای که $$x = f (f^{-1} (x) )$$ همواره برقرار است.

برای مثال، در تصویر زیر اگر $$f$$ تابعی یک به یک و $$f^{-1}$$ وارون یا معکوس آن باشد، تبدیلات $$f$$ و $$f^{-1}$$ به شکل زیر خواهد بود:

شناخت این ویژگی‌ها در مورد یک تابع به ما کمک می‌کند تا در رسم نمودار آن یا محاسبه مشتق و ... بهتر عمل کنیم. برای مثال، اگر بدانیم تابعی زوج است، بلافاصله نتیجه می‌گیریم که نمودار آن نسبت به محور قائم تقارن دارد و این در رسم نمودار تابع کمک کننده است. همچنین انواع تابع را بر اساس ضابطه آن‌ها می‌توان به شکل زیر دسته‌بندی کرد:

• تابع ثابت: تابعی که مقدار آن به ازای هر ورودی یا $$x$$ برابر با عدد ثابتی مانند $$c$$ است ($$f(x) = c$$).
• تابع همانی: تابعی است که مقدار یا خروجی آن یعنی $$f(x)$$ همواره با ورودی یا $$x$$ برابر است ($$f(x) = x$$).
• تابع چند جمله‌ای: تابعی است که از مجموع چند جمله شامل توان‌های صحیح و غیرمنفی $$x$$ ساخته شده است ($$f(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n$$).
• تابع خطی: نوعی تابع چند جمله‌ای است که در آن بیشترین درجه یا توان $$x$$ برابر با یک است ($$f(x) = mx + b$$).
• تابع درجه دو یا مربعی: نوعی تابع چند جمله‌ای است که در آن بیشترین درجه یا توان $$x$$ برابر است با دو ($$f(x) = ax^2 + bx + c$$).
• تابع درجه سه یا مکعبی: نوعی تابع چند جمله‌ای است که در آن بیشترین درجه یا توان $$x$$ برابر است با سه ($$f(x) = ax^3 + bx^2 + c x + d$$).
• تابع گویا: تابعی است که صورت و مخرج آن چندجمله‌ای است با این شرط که مخرج صفر نشود ($$f(x) = \frac {P(x)}{Q(x)}$$ و $$Q(x) \neq 0$$).
• تابع قدر مطلق: تابعی است که فقط مقدار مثبت $$x$$ یا صفر آن را به ما می‌دهد ($$|x| = \begin{cases} x & x \geq 0\\ -x & x < 0\end{cases}$$).
• تابع جزء صحیح یا تابع پله‌ای: تابعی است که بزرگترین عدد کوچکتر یا مساوی $$x$$ را به ما می‌دهد ($$f(x) = [x]$$).
• تابع رادیکالی یا ریشه دوم: تابعی که در آن از متغیر $$x$$ ریشه‌ $$n$$ام گرفته می‌شود ($$f(x) = \sqrt[n]{x}$$).
• تابع مثلثاتی: در این نوع از توابع نسبت‌های اضلاع مثلث قائم‌الزاویه برحسب زاویه تعریف می‌شود ($$f(x) = \sin x$$ و $$f(x) = \cos x$$ و ...).

برای نمونه اگر بخواهیم تابع جزء صحیح را بهتر بشناسیم، لازم است ابتدا تعریف آن را بدانیم. جزء صحیح متغیری مانند $$x$$ به صورت زیر تعریف می‌شود که در آن $$x$$ عدد حقیقی و $$n$$ عدد صحیح است:

$$[x] = n \ , \ n \leq x \leq n+1$$

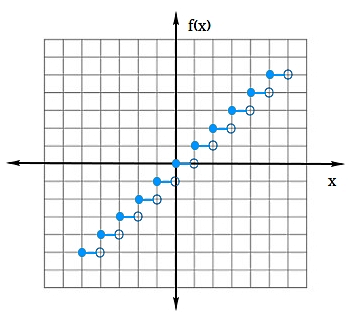
طبق این تعریف برای مثال داریم $$[3.501] = 3$$ یا $$[-1.88] = -2$$. دقت کنید نمودار تابع $$f(x) = [x ]$$ پیوسته نیست، بلکه طبق شکل بالا متشکل است از تعدادی خطوط موازی محور افق که یک تابع پله‌ای را نمایش می‌دهند. همچنین نقطه سمت چپ هر پله توپر است، به این معنا که این نقاط عضوی از مقادیر تابع هستند، در حالی که نقاط سمت راست توخالی هستند، یعنی این نقاط جزئی از تابع محسوب نمی‌شوند. همان‌طور که ملاحظه می‌کنید، مقدار این تابع در تمام بازه‌ها ثابت است.

حل مثال و تمرین از تابع

در این بخش با حل چند نمونه سوال در قالب سوالات تشریحی و چهار گزینه‌ای به شما کمک می‌کنیم تا به مباحث این بخش از آموزش حسابان یازدهم کاملا مسلط شوید.

مثال ۱

اگر توابع $$f$$ و $$g$$ به شکل زیر داده شوند، $$gof$$ را محاسبه کنید:

$$f(x) = \sqrt{x-2}$$

$$g(x) = \ln (1+x^2)$$

پاسخ

دقت کنید در این سوال $$gof$$ یا $$g(f(x))$$ خواسته شده است، نه $$f(g(x))$$. پس به شکل زیر پیش می‌رویم:

$$g(x) = \ln (1+x^2) \Rightarrow g(f(x)) = \ln (1+f^2(x))$$

در این عبارت توان دوم تابع $$f(x)$$ را داریم که برابر است با:

$$f(x) = \sqrt{x-2} \Rightarrow f^2(x) = x-2$$

پس خواهیم داشت:

$$\Rightarrow gof = g(f(x)) = \ln (1+x-2) = \ln (x-1)$$

مثال ۲

معکوس تابع $$f(x) = 5x + 4$$ را پیدا کنید:

پاسخ

در این سوال داریم $$y = 5x + 4$$ و اولین قدم برای پیدا کردن وارون تابع داده شده این است که $$x$$ را پیدا کنیم:

$$x = \frac{y-4}{5}$$

حالا برای نوشتن معکوس کافی است به‌جای $$y$$ از $$x$$ و به جای $$x$$ از $$f^{-1} (x)$$ استفاده کنیم:

$$f^{-1} (x) = \frac{x-4}{5}$$

مثال ۳

دامنه و برد تابع زیر را پیدا کنید:

$$f (x) = -3 \sqrt{14+ 3y}$$

پاسخ

تابع داده شده یک تابع رادیکالی است و می‌دانیم هر عبارتی که زیر رادیکال قرار داده شود، باید مثبت یا مساوی صفر شود. به این ترتیب داریم:

$$\sqrt{14+ 3y} \geq 0$$

$$y \geq \frac{-14}{3}$$

بنابراین دامنه این تابع در زبان ریاضیات و به شکل دقیق برابر است با:

$$D : \ \frac{-14}{3} \leq y \leq +\infty$$

یا

$$D: \ [ \frac{-14}{3} , +\infty )$$

در مورد برد این تابع باید توجه کنیم که در $$y = \frac{-14}{3}$$ عبارت زیر رایکال برابر با صفر می‌شود و در نتیجه مقدار تابع نیز برابر با صفر خواهد شد. اما در مورد سایر مقادیر دامنه، همواره حاصل رادیکال برابر با یک عدد مثبت است که با ضرب شدن در عدد منفی $$-3$$ حاصل کلی منفی خواهد شد. بنابراین بهترین بازه برای برد این تابع به شکل زیر است:

$$R: \ ( -\infty , 0]$$

دقت کنید معمولا دامنه را با $$D$$ و برد را با $$R$$ نشان می‌دهند.

مثال ۴

معادله زیر را حل کنید:

$$[x^2 - 4x ] = 2x -5$$

پاسخ

معادله داده شده یک تابع جزء صحیح است. می‌دانیم تعریف جزء صحیح به این صورت است که اگر داشته باشیم $$[A ] = k$$ به این معنا است که $$k$$ بزرگترین عدد صحیح کوچکتر یا مساوی $$A$$ است. این تعریف دو شرط مهم را ایجاد می‌کند:

• برقراری نامساوی $$k \leq A \leq k+1$$
• عدد صحیح بودن $$k$$

با این توضیح، حل مسئله را به این شکل پیش می‌بریم که معادله داده شده را با $$[A ] = k$$ مقایسه می‌کنیم:

$$x^2 - 4x = A$$

$$2x -5 = k$$

و بلافاصله ابتدا شرط عدد صحیح بودن عبارت $$2x -5$$ را در نظر می‌گیریم. سپس نامعادله $$k \leq A \leq k+1$$ را به شکل $$2x -5 \leq x^2 - 4x \leq 2x -4$$ خواهیم داشت. حل این نامعادله باید در دو مرحله انجام شود، در واقع یک دستگاه نامعادلات به شکل زیر داریم:

$$\begin{cases} 2x -5 \leq x^2 - 4x \\x^2 - 4x \leq 2x -4 \end{cases}$$

مجموعه جواب این سوال با اشتراک گرفتن از جواب‌های این دو نامعادله و البته در نظر گرفتن شرط مربوط به عدد صحیح شدن جواب عبارت $$2x -5$$ حاصل خواهد شد. اولین نامعادله برابر می‌شود با:

$$0 \leq x^2 - 4x -2x + 5$$

$$0 \leq x^2 -6x + 5$$

حالا معادله $$x^2 -6x + 5 =0$$ را در نظر گرفته و با تجزیه آن به یک اتحاد جمله مشترک ریشه‌ها را پیدا می‌کنیم:

$$(x - 1)(x-5) = 0 \Rightarrow x= 1 , x= 5$$

چون ضریب $$x^2$$ مثبت است، پس نامعادله در خارج ریشه‌ها برقرار است. در واقع این معادله نشان دهنده یک سهمی رو به بالا است، پس نامعادله داده شده پاسخ‌‌هایی در بازه زیر دارد:

$$x \in (- \infty , 1 ] \cup [5, + \infty)$$

حالا می‌رویم سراغ نامعادله دیگر که به شکل زیر است:

$$x^2 - 4x \\x^2 - 4x \leq 2x -4$$

$$x^2 - 6x + 4 \leq 0$$

حل معادله $$x^2 - 6x + 4 = 0$$ به روش دلتا منجر به دو ریشه $$3 \pm \sqrt{5}$$ خواهد شد. این نامعادله بین ریشه‌ها برقرار است، بنابراین بازه مناسب برای پاسخ آن به صورت زیر خواهد شد:

$$x \in (3 - \sqrt{5}, 3 + \sqrt{5})$$

در آخرین مرحله لازم است اشتراک بین این دو بازه را پیدا کنیم. اگر با تقریب $$\sqrt{5}$$ را برابر $$2.23$$ در نظر بگیریم، داریم:

$$3 - \sqrt{5} \approx 0.76$$

$$3 + \sqrt{5} \approx 5.23$$

$$( (- \infty , 1 ] \cup [5, + \infty) )\cap ( (3 - \sqrt{5}, 3 + \sqrt{5}) )$$

$$= (3 - \sqrt{5}, 1 ] \cap [5, 3 + \sqrt{5})$$

اما از این مجموعه پاسخ فقط آن جواب‌هایی قابل‌قبول هستند که $$2x-5$$ را به یک عدد صحیح تبدیل می‌کنند. اگر فرض کنیم $$x \in (3 - \sqrt{5}, 1 ]$$ باشد:

$$2(3 - \sqrt{5}) -5 < 2x-5 \leq 2(1) - 5$$

با در نظر گرفتن $$2x- 5 = k$$، خواهیم داشت:

$$1 - 2\sqrt{5} < k \leq -3$$

$$-3.47 < k \leq -3$$

تنها عدد صحیح در این بازه $$k = -3$$ است. در نتیجه برای $$x$$ داریم:

$$2x - 5 = -3 \Rightarrow x = 1$$

مقدار $$1$$ در بازه $$(3 - \sqrt{5}, 1 ]$$ قرار دارد، پس قابل‌قبول است. در حالت بعدی فرض می‌کنیم که $$x \in [5, 3 + \sqrt{5})$$:

$$2(5) -5 \leq 2x-5< 2(3 + \sqrt{5}) -5$$

$$5 \leq k< 2\sqrt{5} + 1$$

$$5 \leq k< 5.47$$

تنها عدد صحیح در این بازه $$k = 5$$ است. در نتیجه برای $$x$$ داریم:

$$2x - 5 = 5 \Rightarrow x = 5$$

مقدار $$5$$ نیز در بازه $$[5,3 + \sqrt{5})$$ قرار دارد، پس قابل‌قبول است. به این ترتیب پاسخ این سوال می‌شود:

$$= { 1,5}$$ جواب‌های قابل‌قبول

توابع نمایی و لگاریتمی

پس از اینکه با انواع تابع و ویژگی‌های کلی یک تابع در فصل دوم آموزش حسابان یازدهم آشنا شدیم، در این بخش روی توابع لگاریتمی و نمایی متمرکز خواهیم شد. پیشنهاد می‌کنیم برای تسلط بیشتر بر سوالات این بخش، فیلم آموزش رایگان محاسبه سریع لگاریتم – روش حل تستی + مثال‌های مختلف فرادرس را مشاهده کنید که لینک آن نیز در ادامه برای شما قرار داده شده است:

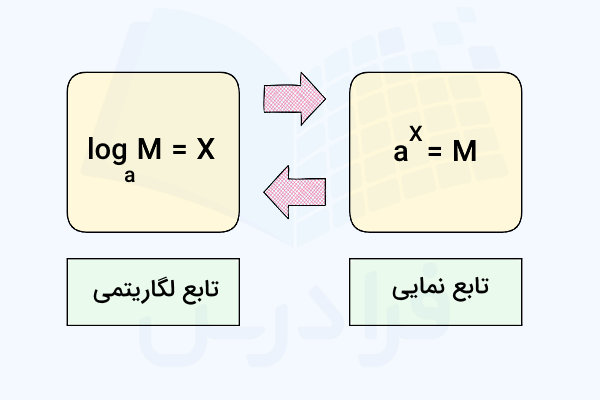
تابع نمایی چیست؟

تابع نمایی یا Exponential Function به تابعی گفته می‌شود که در آن متغیر $$x$$ در توان یا نمای یک عدد ثابت مانند $$b$$ ظاهر می‌شود. ضابطه کلی این تابع به شکل زیر تعریف می‌شود:

$$f(x) = b^x$$

که البته لازم است شرایطی مانند $$b \neq 1$$ و $$0 < b$$ نیز همواره برقرار باشند تا بتوانیم چنین تابعی را یک تابع نمایی بنامیم. نمودار تابع نمایی به شکل زیر است و همان‌طور که ملاحظه می‌کنید، این تابع یک تابع یک به یک محسوب می‌شود:

همچنین این تابع معکوس تابع لگاریتمی است و به همین دلیل در بخش بعد پس از تعریف لگاریتم به بررسی ارتباط این دو تابع خواهیم پرداخت. بررسی رشد جمعیت و میزان سرمایه‌گذاری در گذر زمان از جمله موضوعاتی هستند که توسط تابع نمایی به خوبی توصیف می‌شوند.

به طور کلی بهتر است قواعد زیر را در مورد توابع نمایی به خاطر بسپاریم:

$$a^0 = 1$$

$$a^{-x} = \frac{1}{a^x}$$

$$a^{x} . a^{y} = a^{x+ y}$$

$$(a^{x} )^y = a^{xy}$$

$$(ab)^x = a^x b^x$$

$$(\frac{a}{b})^x = \frac{a^x}{b^x}$$

$$\frac{a^x}{a^y} = a^{x-y}$$

تابع لگاریتمی چیست؟

تابع لگاریتمی معکوس تابع نمایی است. اگر تابع نمایی ما به شکل $$f(x) = b^x$$ باشد، معکوس آن یا تابع لگاریتمی متناظر با آن را با $$g(x)$$ نشان می‌دهیم که به صورت زیر است:

$$g(x) = \log _b (x)$$

با این شروط که داشته باشیم: $$b \neq 1$$ و $$0 < b$$. همان‌طور که ملاحظه می‌کنید محدودیت‌‌های $$b$$ برای هر دو نوع تابع یکسان است، چون این دو تابع وارون هم هستند. از این موضوع می‌‌توانیم به این نتیجه برسیم که برای تمام $$0 < x$$ داریم:

$$b^ { \log _b (x)} = x$$

$$\log _b {b^x} = x$$

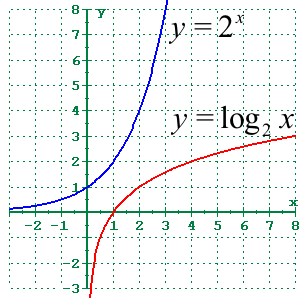
در مورد توابع لگاریتمی نکات زیر مهم هستند:

• عموما تابع $$f(x) = \log_{10} ( x)$$ به شکل $$f(x) = \log ( x)$$ نوشته می‌شود.
• برای تابع لگاریتمی به شکل $$g(x) = \log_{e} ( x)$$ نیز تابع جدیدی به صورت $$g(x) = \ln x$$ تعریف می‌شود که لگاریتم طبیعی نام دارد.
• در لگاریتم طبیعی $$e \approx 2.71828$$ عدد نپر نامیده می‌شود.
• اگر داشته باشیم $$a = b^c$$ ، آنگاه شکل لگاریتمی این تساوی برابر است با $$c = \log _b a$$.

همچنین مهم‌ترین قوانین در مورد لگاریتم‌ها را می‌توان به شکل زیر فهرست کرد:

$$\log_{b} ( x^a) = a \log_b (x)$$

$$\log_{b} (xy) = \log_{b} (x) + \log_{b} (y)$$

$$\log_{b} (\frac{x}{y}) = \log_{b} (x) - \log_{b} (y)$$

$$\log_{a} (b) = \frac{1}{\log_{b} (a) }$$

$$\log_{b} (x) = \frac{\log_{c} (x)}{\log_{c} (b) }$$

حل مثال و تمرین از تابع نمایی و لگاریتمی

در این قسمت با حل چند نمونه سوال مباحث این فصل از آموزش حسابان یازدهم را عمیق‌تر خواهید آموخت.

مثال ۱

عبارت لگاریتمی زیر را ساده کنید:

$$5\log_{2} (x) + 3\log_{2} (2y)$$

پاسخ

ساده کردن عبارت داده شده را به شکل زیر انجام می‌دهیم:

$$5\log_{2} (x) + 3\log_{2} (2y) = \log_{2} (x^5) + \log_{2} ((2y)^3)$$

$$= \log_{2} (x^5) + \log_{2} (8y^3)$$

$$= \log_{2} [(x^5) (8y^3)]$$

$$= \log_{2} (8x^5y^3)$$

مثال ۲

معادله $$4^{2y+1} = 2^{y-1}$$ را برای $$y$$ حل کنید:

پاسخ

برای حل معادلات این چنینی بهتر است ابتدا به پایه‌های دو طرف تساوی دقت کنیم و ببینیم چطور می‌شود آن‌ها را به هم تبدیل کرد. در این سوال دو عدد دو و چهار با هم مرتبط‌اند، چهار توان دوم دو است. پس خواهیم داشت:

$$(2^2)^{2y+1} = 2^{y-1}$$

$$2^{2(2y+1)} = 2^{y-1}$$

$$2^{4y+2} = 2^{y-1}$$

حالا که پایه‌‌های هر دو عدد توان‌دار در دو طرف تساوی با هم برابر شدند، نما یا توان آن‌ها نیز با هم برابر است. بنابراین داریم:

$$4y+2 = y-1 \Rightarrow 3y = -3 \Rightarrow y = -1$$

مثلثات

در چهارمین فصل از آموزش حسابان یازدهم مباحثی مانند رادیان، نسبت‌های مثلثاتی برخی از زاویه‌ها، توابع مثلثاتی و بررسی روابط مثلثاتی مجموع یا تفاضل زاویه‌ها بررسی می‌شود.

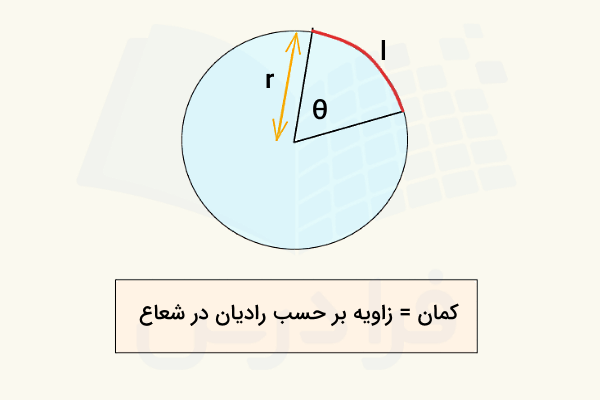
رادیان چیست؟

مثلثات با تسلط بر جداول حاصل از دایره مثلثاتی شروع می‌شود و دانستن این نکته که زاویه‌ها به جای درجه اغلب با واحد دیگری به نام رادیان توصیف می‌شوند، ضروری است. محاسبه اندازه یک زاویه بر حسب رادیان توسط رابطه زیر انجام می‌شود که در آن $$l$$ برابر است با طول کمان روبروی زاویه $$\theta$$ در دایره‌ای به شعاع $$r$$:

$$\theta = \frac{l}{r}$$

نسبت های مثلثاتی

در مرحله بعد از این بخش آموزش حسابان یازدهم، بهتر است با تعریف چهار تابع مثلثاتی مهم یعنی سینوس، کسینوس، تانژانت و کتانژانت یک زاویه آشنا شویم که با در نظر گرفتن مثلث قائم‌الزاویه زیر در دایره مثلثاتی حاصل می‌شود:

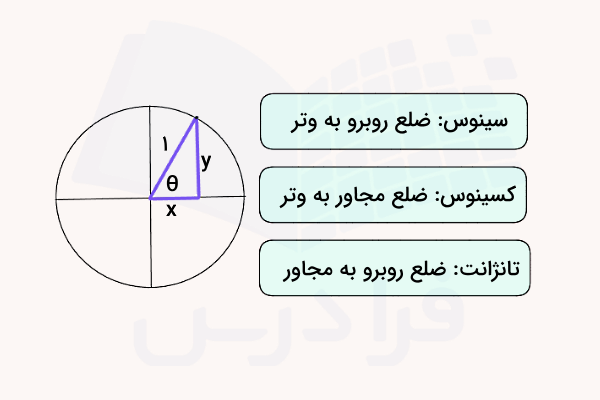
طبق این تعریف‌ها برای دایره بالا با شعاع واحد خواهیم داشت:

$$\sin \theta = \frac{y}{1} = y$$

$$\cos \theta = \frac{x}{1} = x$$

$$\tan \theta = \frac{y}{x}$$

چون همیشه کتانژانت یک زاویه عکس تانژانت آن است، پس داریم:

$$\cot \theta = \frac{x}{y}$$

در ادامه بهتر است روابط زیر را در مورد نسبت‌های مثلثاتی به خاطر بسپاریم. این فرمول‌های به شما کمک می‌کنند تا در حل مسائل این بخش از آموزش حسابان یازدهم سریعتر عمل کنید:

• نسبت‌های مثلثاتی زاویه‌های قرینه:

$$\sin (-\alpha) = - \sin \alpha$$

$$\cos (-\alpha) = \cos \alpha$$

$$\tan (-\alpha) = - \tan \alpha$$

$$\cot (-\alpha) = - \cot \alpha$$

• نسبت‌های مثلثاتی زاویه‌های متمم (زاویه‌هایی که مجموع آن‌ها برابر با $$\frac{\pi}{2}$$ می‌شود):

$$\sin (\frac{\pi}{2} - \theta) = \cos \theta$$

$$\cos (\frac{\pi}{2} - \theta) = \sin \theta$$

$$\tan (\frac{\pi}{2} - \theta) = \cot \theta$$

$$\ cot (\frac{\pi}{2} - \theta) = \tan \theta$$

• نسبت‌های مثلثاتی زاویه‌های مکمل (زاویه‌هایی که مجموع آن‌ها برابر با $$\pi$$ می‌شود):

$$\sin (\pi - \theta) = \sin \theta$$

$$\cos (\pi - \theta) = -\cos \theta$$

$$\tan (\pi - \theta) = - \tan \theta$$

$$\ cot (\pi - \theta) = -\cot \theta$$

• نسبت‌های مثلثاتی زاویه‌های بزرگتر از $$\pi$$:

$$\sin (\pi + \theta) = -\sin \theta$$

$$\cos (\pi+\theta) = -\cos \theta$$

$$\tan (\pi + \theta) = \tan \theta$$

$$\ cot (\pi + \theta) =\cot \theta$$

• نسبت‌های مثلثاتی زاویه‌‌های دارای مجموع یا تفاضل $$2k\pi$$ رادیان:

$$\sin (2k\pi + \theta) = \sin \theta$$

$$\cos (2k\pi+\theta) = \cos \theta$$

$$\tan (2k\pi + \theta) = \tan \theta$$

$$\ cot (2k\pi + \theta) =\cot \theta$$

$$\sin (2k\pi - \theta) =- \sin \theta$$

$$\cos (2k\pi - \theta) = \cos \theta$$

$$\tan (2k\pi - \theta) = -\tan \theta$$

$$\ cot (2k\pi - \theta) =-\cot \theta$$

• نسبت‌های مثلثاتی زاویه‌‌های دارای مجموع $$\frac{\pi}{2}$$ رادیان:

$$\sin ( \frac{\pi}{2} + \theta) =\cos \theta$$

$$\cos ( \frac{\pi}{2} + \theta) =- \sin \theta$$

$$\tan ( \frac{\pi}{2} + \theta) = -\cot \theta$$

$$\ cot ( \frac{\pi}{2} + \theta) =-\tan \theta$$

توابع مثلثاتی

در بخش انواع تابع از آموزش حسابان یازدهم با انواع تابع آشنا شدید. به توابعی مانند $$y = \sin x$$ و $$y = \cos x$$ و $$y = \cos x$$ و $$y = \cos x$$ توابع مثلثاتی گفته می‌شود. البته توابع مثلثاتی دیگری مانند سکانت یا $$y = \sec x$$ و کسکانت یا $$y = \cosec x$$ نیز داریم که به شکل زیر تعریف می‌شوند:

$$\sec x = \frac{1}{\cos x}$$

$$\cosec x = \frac{1}{\sin x}$$

در ادامه مهم‌ترین ویژگی‌های توابع مثلثاتی را برای شما فهرست کرده‌ایم:

• دامنه توابع سینوسی و کسینوسی معادل است با مجموعه اعداد حقیقی.
• برد توابع سینوسی و کسینوسی همواره در بازه بسته $$[-1,+1]$$ قرار می‌گیرد.
• دامنه توابع تانژانتی شامل تمام اعداد حقیقی به جز مضارب فرد $$\frac{\pi}{2}$$ مانند $$\frac{3\pi}{2}$$ یا $$\frac{-\pi}{2}$$ است.
• دامنه توابع کتانژانتی شامل تمام اعداد حقیقی به جز مضارب صحیح $$\pi$$ مانند $$3\pi$$ یا $$-\pi$$ است.
• برد توابع تانژانت و کتانژانت معادل است با مجموعه اعداد حقیقی.

نحوه رسم نمودار این توابع را در مطالب «رسم نمودار سینوس و کسینوس – به زبان ساده با مثال و تمرین» و «نمودار تانژانت و کتانژانت – به زبان ساده با مثال و تمرین» از مجله فرادرس به طور کامل توضیح داده‌ایم.

روابط مثلثاتی مجموع و تفاضل دو زاویه مختلف

روابط مثلثاتی مجموع و تفاضل دو زاویه مختلف به شکل زیر تعریف می‌شوند:

$$\sin (\alpha + \beta) = \sin \alpha \cos \beta + cos \alpha \sin \beta$$

$$\cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$$

$$\sin (\alpha - \beta) = \sin \alpha \cos \beta - cos \alpha \sin \beta$$

$$\cos (\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta$$

حل مثال و تمرین از مثلثات

پس از اینکه با مهم‌ترین روابط مثلثاتی در حسابان یک آشنا شدیم، در این قسمت چند نمونه سوال در این زمینه حل می‌کنیم. پیش از شروع چند فرمول دیگر را نیز معرفی می‌کنیم که تسلط بر آن‌ها در حل مسائل مثلثات بسیار مهم است:

$$\sin^2\theta + \cos^2\theta = 1$$

$$\cos2\theta =2 \cos^2\theta -1$$

$$\sin2\theta =2 \sin\theta \cos\theta$$

$$1+ \tan^2\theta = \sec^2\theta$$

$$1+ \cot^2\theta = \csc^2\theta$$

مثال ۱

برای هر کدام از معادلات زیر به کمک روابط مثلثاتی مجموعه پاسخ‌های ممکن را پیدا کنید:

$$1+ \cos(2\theta) = \cos\theta$$

$$\sin(2\theta) = \tan\theta$$

پاسخ

در مورد اولین معادله از فرمول زیر استفاده می‌کنیم:

$$\cos2\theta =2 \cos^2\theta -1$$

$$1+2 \cos^2\theta -1 = \cos\theta \Rightarrow 2 \cos^2\theta - \cos\theta = 0$$

برای حل این معادله، از $$\cos\theta$$ فاکتورگیری می‌کنیم و سپس پاسخ هر بخش را پیدا می‌کنیم:

$$\Rightarrow \cos\theta \ (2 \cos\theta - 1) = 0$$

در اولین حالت $$\cos\theta = 0$$ است، پس داریم:

$$\theta = \frac{\pi}{2}, \frac{\pi}{2}\pm \pi, \frac{\pi}{2}\pm 2\pi , ...$$

در حالت بعدی $$\cos\theta = \frac{1}{2}$$ است، پس داریم:

$$\theta = \frac{\pi}{3}, \frac{\pi}{3}\pm 2\pi , ...$$

یا

$$\theta =- \frac{\pi}{3}, - \frac{\pi}{3}\pm 2\pi , ...$$

با توجه به این سه مجموعه می‌توانیم جواب این معادله را برای $$n = 0, \pm1, \pm 2, \pm3, ...$$ به شکل کلی زیر در نظر بگیریم:

$$\theta = \frac{\pi}{2} + n\pi$$

$$\theta = \frac{\pi}{3} + 2n\pi$$

$$\theta = -\frac{\pi}{3} + 2n\pi$$

در مورد دومین معادله از فرمول $$\sin2\theta =2 \sin\theta \cos\theta$$ برای سمت چپ تساوی استفاده می‌کنیم و در سمت راست نیز تانژانت را بر حسب سینوس و کسینوس می‌نویسیم:

$$2 \sin\theta \cos\theta = \frac {\sin \theta}{\cos\theta}$$

$$\Rightarrow 2 \sin\theta \cos^2\theta- \sin \theta = 0$$

با فاکتورگیری از سینوس خواهیم داشت:

$$\Rightarrow \sin\theta (2 \cos^2\theta- 1) = 0$$

مجددا به دو عبارت رسیدیم که ضرب‌شان در هم برابر با صفر شده است. پس لازم است هر کدام را جداگانه برابر با صفر در نظر بگیریم:

$$\sin\theta = 0$$

$$\Rightarrow \theta =0 , \pm\pi , \pm 2\pi, ...$$

$$2 \cos^2\theta- 1 = 0$$

$$\Rightarrow \cos^2\theta = \frac{1}{2}$$

$$\Rightarrow \theta =\frac{\pi}{4} ,\frac{\pi}{4} \pm \frac{\pi}{2}, \frac{\pi}{4}\pm \pi, ...$$

به این ترتیب مجموعه جواب‌‌های این معادله برای $$n = 0, \pm1, \pm 2, \pm3, ...$$ در حالت کلی عبارت‌اند از:

$$\theta = n\pi$$

$$\theta =\frac{\pi}{4} + \frac{n\pi}{2}$$

مثال ۲

عبارت مثلثاتی $$\frac{\sin(\frac{3\pi}{2}-x) - \cos (5\pi +x)}{\sin(\pi +x) +\cos (\frac{\pi}{2}+x)}$$ را ساده کنید:

پاسخ

از روابط زیر استفاده می‌کنیم تا تک تک جملات را ساده کنیم:

$$\sin(\frac{3\pi}{2}-x )= -\cos x$$

$$\cos(\frac{\pi}{2}+x )= -\sin x$$

$$\cos(5\pi+x )= -\cos x$$

$$\sin(\pi+x )= -\sin x$$

به این ترتیب خواهیم داشت:

$$\Rightarrow \frac{-\cos x - (-\cos x)}{-\sin x +(-\sin x)} = \frac{-\cos x +\cos x}{-2\sin x} = 0$$

یادگیری ریاضی متوسطه دوم با فرادرس

در این مطلب از مجله فرادرس روی آموزش حسابان یازدهم تمرکز کردیم. مقطع متوسطه دوم رشته ریاضی و فیزیک شامل دروس دیگری از جمله هندسه تحلیلی، آمار و احتمال و ریاضیات گسسته است. در این بخش می‌توانید چند فیلم آموزشی فرادرس در این زمینه را مشاهده کنید:

• فیلم آموزش آمار و احتمال پایه یازدهم
• فیلم آموزش هندسه ۳ پایه دوازدهم رشته ریاضی و فیزیک
• فیلم آموزش ریاضیات گسسته پایه دوازدهم

حد و پیوستگی

در آخرین مبحث از آموزش حسابان یازدهم با مفهوم حد، فرآیندهای حدی، حد چپ و راست، قضایای حد و قوانین مربوط به رفع ابهام‌های حد آشنا می‌شوید. همچنین شرایط لازم برای برقراری پیوستگی در یک تابع را خواهید آموخت.

مفهوم حد

مفهوم حد یا لیمیت (Limit) به منظور توصیف رفتار یک تابع در نزدیکی یا همسایگی یک نقطه خاص بکار می‌رود. در این توصیف نیازی نداریم که لزوما خود تابع در آن نقطه تعریف شده باشد. این توضیح به این معنا است که ممکن است تابعی در یک نقطه مقدار تعریف شده‌ای نداشته باشد، اما با بررسی حد آن در نزدیکی این نقطه می‌توانیم رفتار حدی تابع را در همسایگی این نقطه بررسی کنیم.

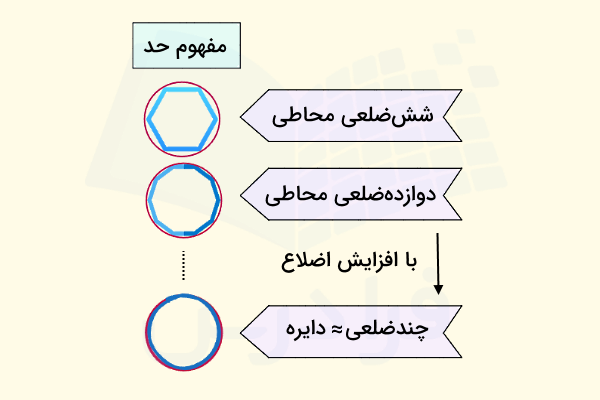
برای مثال، فرض کنید یک شش ضلعی منتظم داخل دایره‌ای قرار دارد. اگر تعداد اضلاع این چندضلعی را افزایش دهیم، برای مثال یک دوازده‌ضلعی منتظم محاطی داشته باشیم، مشاهده می‌کنید که مساحت این چندضلعی بسیار به مساحت دایره نزدیک شده است. به همین شکل با افزایش بیشتر تعداد اضلاع چندضلعی می‌توانیم نتیجه‌گیری کنیم که مساحت چند ضلعی به سمت مساحت دایره میل می‌کند. به بیان دیگر، مساحت دایره برابر است با حد مساحت چندضلعی، زمانی که تعداد اضلاع آن بسیار بسیار زیاد شود.

مهم‌ترین تعریف‌هایی که لازم است برای درک مفهوم حد بدانید، شامل موارد زیر است:

• همسایگی $$x_0$$: اگر $$x_0 \in (a,b)$$ باشد، بازه $$(a,b)$$ را به شکل همسایگی $$x_0$$ تعریف می‌کنیم.
• همسایگی محذوف $$x_0$$: اگر $$x_0$$ را از بازه $$(a,b)$$ حذف کنیم، مجموعه $$(a,b) - \left\{x _0\right\}$$ همسایگی محذوف $$x_0$$ نامیده می‌شود.
• همسایگی راست $$x_0$$: اگر $$r$$ یک عدد مثبت باشد، بازه $$(x _0, x _0+r)$$ را یک همسایگی راست آن می‌نامیم.
• همسایگی چپ $$x_0$$: اگر $$r$$ یک عدد مثبت باشد، بازه $$(x _0 -r, x _0)$$ را یک همسایگی چپ آن می‌نامیم.
• حد تابع $$f$$: حد تابع $$f(x )$$ هنگامی که $$x$$ به سمت $$a$$ میل می‌کند، برابر است با عدد حقیقی $$L$$ و به صورت $$\lim_{x \rightarrow a} f(x ) = L$$ نمایش داده می‌شود، اگر با نزدیک شدن $$x$$ به $$a$$، مقادیر $$f$$ نیز به سمت $$L$$ نزدیک شوند.
• شرط وجود حد در یک نقطه: برای اینکه در یک نقطه حد وجود داشته باشد، لازم است حد راست و چپ در آن نقطه با هم برابر باشند.

در بخش بعد راجع‌به حد راست و چپ یا همان حدود یک‌طرفه بیشتر توضیح خواهیم داد.

حد چپ و راست چیست؟

گفتیم شرط وجود حد در یک نقطه این است که حد راست و چپ در آن نقطه با هم برابر باشند. برای محاسبه حدود یک طرفه لازم است همسایگی راست و چپ تابع را در نظر بگیریم. در حد راست فقط مقادیری از $$x$$ را در نظر می‌گیریم که از $$a$$ بزرگتر هستند، در حالی که برای حد چپ فقط مقادیری از $$x$$ را در نظر می‌گیریم که از $$a$$ کوچکتراند. پس تعریف دقیق‌تر حدهای یک‌طرفه به شکل زیر است:

$$\lim_{x \rightarrow a^+} f(x )$$ = حد راست

$$\lim_{x \rightarrow a^-} f(x )$$ = حد چپ

حد $$\lim_{x \rightarrow a} f(x )$$ زمانی وجود دارد که رابطه زیر برقرار باشد:

$$\lim_{x \rightarrow a^+} f(x ) = \lim_{x \rightarrow a^-} f(x ) = L$$

این توضیح به این معنا است که اگر حد راست و چپ یک تابع برای یک نقطه با هم برابر نشوند، در آن نقطه حد نداریم.

نکته: اگر دو تابع مختلف مانند $$f$$ و $$g$$ داشته باشیم که در همسایگی نقطه‌ای مانند $$a$$ با هم برابراند، در این صورت حد این دو تابع نیز در نقطه $$a$$ و در صورت وجود با هم برابر است.

قضایای حد

پس از اینکه با تعریف و مفهوم حد در بخش‌های قبل آموزش حسابان یازدهم کاملا آشنا شدیم، لازم است به قضایای حد نیز کاملا مسلط شویم:

• حد تابع ثابت: حد تابع $$f(x) = c$$ در هر نقطه دلخواهی مانند $$a$$ برابر است با عدد ثابت $$c$$، یعنی $$\lim_{x \rightarrow a}c = c$$.
• حد تابع همانی: حد تابع $$f(x) = x$$ در هر نقطه دلخواهی مانند $$a$$ برابر است با $$a$$، یعنی $$\lim_{x \rightarrow a}x = a$$.
• حد توابع چند جمله‌ای، مثلثاتی و گویا: حد این توابع در هر نقطه دلخواهی مانند $$a$$ برابر است با مقدار این توابع در این نقطه.
• حد مجموع دو تابع: اگر $$\lim_{x \rightarrow a} f = L_1$$ و $$\lim_{x \rightarrow a} g = L_2$$، آنگاه $$\lim_{x \rightarrow a} (f+g) = L_1 + L_2$$.
• حد تفاضل دو تابع: اگر $$\lim_{x \rightarrow a} f = L_1$$ و $$\lim_{x \rightarrow a} g = L_2$$، آنگاه $$\lim_{x \rightarrow a} (f-g) = L_1 - L_2$$.
• حد حاصل‌ضرب دو تابع: اگر $$\lim_{x \rightarrow a} f = L_1$$ و $$\lim_{x \rightarrow a} g = L_2$$، آنگاه $$\lim_{x \rightarrow a} (f.g) = L_1 . L_2$$.
• حد خارج‌قسمت: اگر $$\lim_{x \rightarrow a} f = L_1$$ و $$\lim_{x \rightarrow a} g = L_2$$ با این شرط که $$L_2$$مخالف صفر است، آنگاه $$\lim_{x \rightarrow a} \frac{f}{g} = \frac{L_1}{L_2}$$.

رفع ابهام صفر صفرم و حد در بی نهایت

در بخش قبل گفتیم حد توابع گویا در هر نقطه دلخواهی مانند $$a$$ برابر است با مقدار این توابع در این نقطه. اما ممکن است پس از جای‌گذاری مستقیم $$x= a$$ حالت مبهمی به نام ابهام صفر صفرم ایجاد شود.  در این شرایط برای رفع ابهام و محاسبه حد از روش‌های زیر استفاده می‌شود:

• فاکتورگیری و ساده‌سازی
• ضرب در مزدوج

همچنین مفهوم دیگری که در حدگیری ممکن است با آن مواجه شویم، حد در بی‌نهایت است که به شکل زیر تعریف می‌شود:

$$\lim_{x \rightarrow \pm \infty } f(x)$$

حد در بی‌نهایت رفتار تابع را زمانی که متغیر $$x$$ بسیار بسیار بزرگ (مثبت یا منفی) می‌شود، بررسی می‌کند. همچنین در مورد توابع گویا، حاصل حد در بی‌نهایت برابر است با نسبت ضرایب بزرگ‌ترین توان‌ها در صورت و مخرج.

پیوستگی

در آخرین مبحث از آموزش حسابان یازدهم، می‌آموزیم که پیوستگی یک تابع به چه معنا است. به زبان ساده پیوسته یعنی اینکه نمودار تابع دارای قطع‌شدگی یا پرش نباشد و بدون برداشتن قلم بتوانیم آن را رسم کنیم. برای مثال، تابع جزء صحیح $$x$$ یک تابع ناپیوسته است. پیوستگی تابع $$f$$ در نقطه‌ای مانند $$x=a$$ با برقراری سه شرط زیر تعریف می‌شود:

1. $$f(a)$$ موجود باشد.
2. $$\lim_{x \rightarrow a } f(x)$$ موجود باشد.
3. $$\lim_{x \rightarrow a } f(x) = f(a)$$

حل مثال و تمرین از حد و پیوستگی

در این بخش به بررسی چند نمونه سوال در مورد حد و پیوستگی از حسابان یک می‌پردازیم.

مثال ۱

حد زیر را محاسبه کنید:

$$L = \lim_{x \rightarrow 2 } \frac{x^2 - 4}{\sqrt{x+2} - 2}$$

پاسخ

اگر $$x= 2$$ را روی تابع داده شده اعمال کنیم، به ابهام صفر صفرم می‌رسیم:

$$\frac{2^2 - 4}{\sqrt{2+2} - 2} = \frac{0}{0}$$

پس لازم است رفع‌ابهام کنیم تا عامل ایجادکننده ابهام یعنی $$x-2$$ حذف شود:

$$L = \lim_{x \rightarrow 2 } \frac{(x-2)(x+2) \times \sqrt{x+2} + 2}{x+2 - 4}= \lim_{x \rightarrow 2 } = [(x+2) \times (\sqrt{x+2} + 2)]$$

در نهایت با جای‌گذاری $$x= 2$$ خواهیم داشت:

$$L = [(2+2) \times (\sqrt{2+2} + 2)] = 16$$

مثال ۲

اگر تابع $$f(x) = \begin{cases} \frac{x^2 -1}{x-1} & x < 1\\2ax+1 & x \geq 1\end{cases}$$ در $$x=1$$ پیوسته باشد، مقدار $$a$$ چقدر است؟

پاسخ

می‌دانیم شرط پیوستگی یک تابع در یک نقطه مشخص این است که حد راست و چپ و مقدار تابع در آن نقطه با هم برابر باشند. ابتدا حد راست و مقدار تابع را در $$x=1$$ طبق ضابطه تابع پیدا می‌کنیم:

$$f(1) = 2a + 1$$

$$\lim_{x \rightarrow 1^+} (2ax+1) = 2a+1$$

حالا حد چپ را محاسبه می‌کنیم که البته نیاز به رفع‌ابهام با فاکتورگیری نیز دارد:

$$\lim_{x \rightarrow 1^-} \frac{x^2 -1}{x-1} = \lim_{x \rightarrow 1^-} \frac{(x-1)(x+1)}{x-1} = 2$$

در نهایت با برابر قرار دادن این مقادیر خواهیم داشت:

$$\Rightarrow 2a+1 = 2 \Rightarrow a = \frac{1}{2}$$